Applying Hybrid Fuzzy Multi-Criteria Decision-Making Approach to Find the Best Ranking for the Soft Constraint Weights of Lecturers in UCTP

Abstract

University course timetabling problem is an NP-hard problem faced periodically by every university of the world which is a time-consuming task. Here, the major goal is to analyze data in order to determine the lecturers’ preferences and constraints and obtain an appropriate ranking to increase their satisfaction by improving it based on soft constraints weights. The proposed method applies a three-step algorithm where in step 1 a fuzzy decision-making approach (fuzzy multi-criteria comparison) is used to prioritize the lecturers; in step 2, a local search algorithm with seven neighborhood structures is employed to improve the ranks by satisfying hard constraints; and in step 3, the genetic algorithm is applied to obtain a proper pattern for adjusting the values of each lecturer’s fitness function. In the proposed algorithm, a list of selective priorities is determined, prioritized and ranked by applying a fuzzy multi-criteria decision-making method based on fuzzy comparison of daily timeslots; then a time table is considered by the combination of local search and genetic algorithms to improve the quality of fitness functions. The proposed method is evaluated by fuzzy multi-criteria decision-making and hybrid algorithms. Here, the dataset of Islamic Azad University, Ahar Branch computer department, is used for simulation. The simulation results show that the proposed method is able to increase the satisfaction of lecturers in terms of their preferences and ranks.

Appendix: Examples of Comparing Two Fuzzy Sets

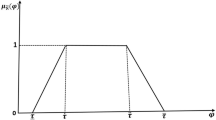
Notes: Default daily timeslots and weekly timeslots are considered in this paper:

$${\text{DailyTimeslots}}= \left\{ {\frac{8 - 9:30}{1},\,\frac{10 - 11:30}{2},\,\frac{12 - 13}{3},\,\frac{13 - 14:30}{4}} \right., \quad \frac{15 - 16:30}{5},\,\frac{17 - 18:30}{6},\,\left. {\frac{19 - 20:30}{7}} \right\} \\$$

$${\text{WeeklyTimeslots}} = \left\{ {\frac{\text{Saturday}}{ 1} ,\,\frac{\text{Sunday}}{ 2} ,\,\frac{\text{Monday}}{ 3} ,\,\frac{\text{Tuesday}}{ 4}} \right., \quad \frac{\text{Wednesday}}{ 5} ,\,\frac{\text{Thursday}}{ 6} ,\,\left. {\frac{\text{Friday}}{ 7}} \right\} \\$$

For example, to convert a fuzzy value to a crisp value, we have:

$$A = \left\{ {\frac{0.5}{1},} \right.\;\frac{0.3}{4},\left. {\frac{0.2}{5}} \right\}.$$

$${\text{Crisp}} = \frac{1 \times 0.5 + 4 \times 0.3 + 5 \times 0.2}{0.5 + 0.3 + 0.2} = \frac{2.7}{1} = 2.7$$

The above method is called center of gravity method.

Note: we have two fuzzy values for each lecturer, where one is for timeslot and the other one is for weekly timeslot.

$$\begin{array}{*{20}c} {\text{This value is for the weekly}} \\ {\text{timeslots of two lecturers }} \\ \end{array} = \left\{\begin{aligned} & L_{1} = \mu_{{\tilde{E}_{i} }} \left( x \right) = \left\{ {\frac{0.7}{5},\frac{0.2}{3},\frac{0.1}{6}} \right\} \hfill \\ & L_{2} = \mu_{{\tilde{E}_{i + 1} }} \left( y \right) = \left\{ {\frac{0.3}{1},\frac{0.3}{2},\frac{0.4}{6}} \right\} \hfill \\ \end{aligned} \right.$$

The fuzzy multi-criteria comparison method:

$$\begin{aligned} T\left( {\tilde{L}_{1} \ge \tilde{L}_{2} } \right)& \Rightarrow \,5_{{\tilde{L}_{1} }} \ge 1_{{\tilde{L}_{2} }} ,\,5_{{\tilde{L}_{1} }} \ge 2_{{\tilde{L}_{2} }} ,\,3_{{\tilde{L}_{1} }} \ge 1_{{\tilde{L}_{2} }} ,\,3_{{\tilde{L}_{1} }} \ge 2_{{\tilde{L}_{2} }} , \hfill \\ & \quad \;\;6_{{\tilde{L}_{1} }} \ge 1_{{\tilde{L}_{2} }} ,\,6_{{\tilde{L}_{1} }} \ge 2_{{\tilde{L}_{2} }} ,\,6_{{\tilde{L}_{1} }} \ge 6_{{\tilde{L}_{2} }} \hfill \\ \end{aligned}$$

$$\begin{aligned} T\left( {\tilde{L}_{1} \ge \tilde{L}_{2} } \right) &= \hbox{max} \,\left\{ {\,\hbox{min} \left( {0.7,\,0.3} \right),\,\hbox{min} \left( {0.7,\,0.3} \right),\,\hbox{min} \left( {0.2,\,0.3} \right)} \right., \hfill \\ &\quad \hbox{min} \left( {0.2,\,0.3} \right),\,\hbox{min} \left( {0.1,\,0.3} \right),\,\hbox{min} \left( {0.1,\,0.3} \right),\,\left. {\hbox{min} \left( {0.1,\,0.4} \right)} \right\}\hfill \\ & = \hbox{max} \,\left\{ {0.3,\,0.3,\,0.2,\,0.2,\,0.1,\,0.1,\,0.1} \right\} = 0.3 \hfill \\ \end{aligned}$$

$$T\left( {\tilde{L}_{1} \ge \tilde{L}_{2} } \right) = 0.3,\;T\left( {\tilde{L}_{2} \ge \tilde{L}_{1} } \right) = 0.4$$

It means that lecturer $\tilde{L}_{2}$ has higher priority over lecturer $\tilde{L}_{1}$, since its fuzzy values are higher.

However, the comparison is performed over the fuzzy value of daily timeslot for each lecturer. It means that a lecturer who has selected some timeslots to teach in 3 days prefers which days to teach.

Example: fuzzy multi-criteria decision-making comparison over daily timeslots priorities of a lecturer $\tilde{L}_{1}?$

$$\begin{array}{*{20}c} {\text{Selections and priorities }} \\ {{\text{of lecturer}}\;\tilde{L}_{1} } \\ \end{array} \;{ = }\left\{ {\begin{array}{*{20}l} {{\text{Monday}}\,{ = }\left\{ {\frac{ 0. 3}{ 1} ,\,\frac{ 0. 3}{ 3} ,\,\frac{ 0. 2}{ 4}} \right\}} \\ {{\text{Wednesday}}\,{ = }\left\{ {\frac{ 0. 4}{ 2} ,\,\frac{ 0. 4}{ 5} ,\,\frac{ 0. 2}{ 4}} \right\}} \\ {{\text{Thursday = }}\left\{ {\frac{ 0. 3}{ 1} ,\,\frac{ 0. 4}{ 3} ,\,\frac{ 0. 1}{ 4}} \right\}} \\ \end{array} } \right.$$

At first, fuzzy multi-criteria decision-making comparisons are done over these three days and then prioritization is also performed over the daily timeslots of that day.

$$\left\{ {\begin{array}{*{20}c} {T\left( {\tilde{3} \ge \,\tilde{5},\,\tilde{6}} \right) = \,\hbox{min} \,\left\{ {\,T\left( {\tilde{3} \ge \,\tilde{5}} \right)\,,\,T\left( {\tilde{3} \ge \,\,\tilde{6}} \right)} \right\} = 0.3} \\ {T\left( {\tilde{5} \ge \,\tilde{3},\,\tilde{6}} \right) = \,\hbox{min} \,\left\{ {\,T\left( {\tilde{5} \ge \,\tilde{3}} \right)\,,\,T\left( {\tilde{5} \ge \,\,\tilde{6}} \right)} \right\} = 0.4} \\ {T\left( {\tilde{6} \ge \,\tilde{3},\,\tilde{5}} \right) = \,\hbox{min} \,\left\{ {\,T\left( {\tilde{6} \ge \,\tilde{3}} \right)\,,\,T\left( {\tilde{6} \ge \,\,\tilde{5}} \right)} \right\} = 0.4} \\ \end{array} } \right.$$

The preferences of lecturer $\tilde{L}_{1}$ in Wednesday and Thursday are higher than Monday.

$$\begin{array}{*{20}c} {\text{The priority of lecturer}} \\ {\tilde{L}_{1} {\text{ in week's days}}} \\ \end{array} { = }\left\{ \begin{aligned} \frac{ 0. 3}{\text{Monday}}\, ,\,\,\frac{ 0. 4}{\text{Wednesday}} ,\hfill \\ \,\,\frac{ 0. 4}{\text{Thursday}} \hfill \\ \end{aligned} \right\}$$

$$\begin{array}{*{20}c} {{\text{The priority of lecturer }}\tilde{L}_{2} } \\ {\text{in week's days}} \\ \end{array} { = }\left\{ \begin{aligned} \frac{ 0. 4}{\text{Saturday}}\, ,\,\,\frac{ 0. 2}{\text{Sunday}} ,\, \hfill \\ \,\frac{ 0. 2}{\text{Thursday}} \hfill \\ \end{aligned} \right\}$$

Note: if two lecturers $\tilde{L}_{1}$ and $\tilde{L}_{2}$ have the same priority in weekly timeslots, then their preferences are evaluated based on this value (the compared preferences in their daily timeslots).

A complete example: the weekly selected timeslots of two lecturers $\tilde{L}_{1}$ and $\tilde{L}_{2}$ are as the following.

$$\tilde{L}_{1} = \left\{ {\frac{0.7}{5}\,,\,\,\frac{0.2}{3},\,\,\frac{0.1}{4}} \right\},\,\,\tilde{L}_{2} = \left\{ {\frac{0.3}{1}\,,\,\,\frac{0.3}{2},\,\,\frac{0.4}{4}} \right\}$$

$T\left( {\tilde{L}_{1} \ge \tilde{L}_{2} } \right) = 0.3,\;T\left( {\tilde{L}_{2} \ge \tilde{L}_{1} } \right) = 0.4$

Then lecturer $\tilde{L}_{1}$ and $\tilde{L}_{2}$ (over the selective preferences of lecturers $\tilde{L}_{1}$ and $\tilde{L}_{2}$ in their weekly timeslots), Now, in daily timeslots and their comparisons for both lecturers $\tilde{L}_{1}$ and $\tilde{L}_{2}$ are based on their daily timeslots selections.

Note: the priority ratio of each lecturer’s daily timeslots over the selections of daily timeslots of each day and over the daily timeslots of each lecturer over their own selections at each day.

However, these comparisons are performed for this purpose that if multiple lecturers involve in one day, based on this prioritization, some of these lecturers are removed from this day and shifted into other days and timeslots. The timeslots of lecturer $\tilde{L}_{1}$ are as the following:

$$\begin{array}{*{20}c} {{\text{The}}\;{\text{timeslots}}\;{\text{of}}\;{\text{lecturer}}\;} \\ {\tilde{L}_{1} } \\ \end{array} = \left\{ {\begin{array}{*{20}c} {{\text{Monday}} = \left\{ {\frac{ 0. 5}{ 1} ,\,\frac{ 0. 3}{ 3} ,\,\frac{ 0. 2}{ 6}} \right\}} \\ {{\text{Wednesday}} = \left\{ {\frac{ 0. 4}{ 2} ,\,\frac{ 0. 4}{ 5} ,\,\frac{ 0. 2}{ 4}} \right\}} \\ {{\text{Thursday}} = \left\{ {\frac{ 0. 3}{ 1} ,\frac{ 0. 4}{ 3} ,\,\frac{ 0. 2}{ 4} ,\;\frac{ 0. 2}{ 5}} \right\}} \\ \end{array} } \right.$$

$$\begin{aligned} T\left( {\tilde{3} \ge \tilde{5},\tilde{6}} \right) = & \hbox{min} \left\{ {T\left( {\tilde{3} \ge \tilde{5}} \right),T\left( {\tilde{3} \ge \tilde{6}} \right)} \right\} = \left\{ {0.3,\;0.3} \right\} \\ = & 0.3 \\ T\left( {\tilde{3} \ge \tilde{5},\tilde{6},\tilde{7}} \right) = & \hbox{min} \left\{ {T\left( {\tilde{3} \ge \tilde{5}} \right),T\left( {\tilde{3} \ge \tilde{6}} \right),T\left( {\tilde{3} \ge \tilde{7}} \right)} \right\} \\ = & \hbox{min} \left\{ {0.3,\;0.3,\;0.3} \right\} = 0.3 \\ \end{aligned}$$

$$\begin{aligned} T\left( {\tilde{3} \ge \tilde{5},\;\tilde{6}} \right),T\left( {\tilde{5} \ge \tilde{3},\;\tilde{6}} \right),T\left( {\tilde{6} \ge \tilde{3},\;\tilde{5}} \right) \hfill \\ T\left( {\tilde{3} \ge \tilde{5}} \right) = 0.3,\;T\left( {\tilde{3} \ge \tilde{6}} \right) = 0.3 \hfill \\ T\left( {\tilde{5} \ge \tilde{3},\;\tilde{6}} \right) = \hbox{min} \left\{ {T\left( {\tilde{5} \ge \tilde{3}} \right),\;T\left( {\tilde{5} \ge \tilde{6}} \right)} \right\} = 0.4 \hfill \\ T\left( {\tilde{5} \ge \tilde{3}} \right) = 0.4,\;T\left( {\tilde{5} \ge \tilde{6}} \right) = 0.4 \hfill \\ T\left( {\tilde{6} \ge \tilde{3},\;\tilde{5}} \right) = \hbox{min} \left\{ {T\left( {\tilde{6} \ge \tilde{3}} \right),T\left( {\tilde{6} \ge \tilde{5}} \right)} \right\} = 0.4 \hfill \\ T\left( {\tilde{6} \ge \tilde{3}} \right) = 0.4,\;T\left( {\tilde{6} \ge \tilde{5}} \right) = 0.4 \hfill \\ \end{aligned}$$

The selection and allocation of daily timeslots of lecturer $\tilde{L}_{1}$ over weekly timeslots or Wednesday and Thursday would have higher priorities in allocating daily timeslots over Monday.

$$\begin{aligned} T\left( {\tilde{3} \ge \,\tilde{5},\;\,\tilde{6}} \right) = \,\hbox{min} \,\left\{ {\,0.3\,,\,\;0.3} \right\} = 0.3\quad {\text{Monday}} \hfill \\ \left\{ {\begin{array}{*{20}c} {T\left( {\tilde{5} \ge \tilde{3},\;\tilde{6}} \right) = { \hbox{min} }\left\{ {0.4,\;0.4} \right\} = 0.4 {\text{Wedesday}}} \\ {T\left( {\tilde{6} \ge \tilde{3},\;\tilde{5}} \right) = { \hbox{min} }\left\{ {0.4,\;0.4} \right\} = 0.4 {\text{Thursday}}} \\ \end{array} } \right\} \hfill \\ \end{aligned}$$

Two selections have the same priority

$$\begin{array}{*{20}c} {{\text{Prioritization}}\;{\text{over}}\;{\text{the}}\;{\text{daily}}} \\ {{\text{timeslots}}\;{\text{of}}\;{\text{lecturer}}\;\tilde{L}_{1} } \\ \end{array} { = }\left\{ \begin{aligned} \frac{ 0. 4}{{{\text{Thursday}}\,}}\, ,\,\,\frac{ 0. 4}{\text{Wednesday}} ,\, \hfill \\ \,\frac{ 0. 3}{{{\text{Monday}}\,}} \hfill \\ \end{aligned} \right\}$$

The priorities of lecturer $\tilde{L}_{1}$ in Wednesday and Thursday are higher than Monday. Now, the timeslots of lecturer $\tilde{L}_{2}$ are as the following:

$${\text{The}}\;{\text{timeslots}}\;{\text{of}}\;{\text{lecturer}}\;\tilde{L}_{2} = \left\{ {\begin{array}{*{20}c} {{\text{Saturday}}\,{ = }\left\{ {\frac{ 0. 2}{ 1} ,\,\frac{ 0. 2}{ 3} ,\,\frac{ 0. 6}{ 7}} \right\}} \\ {{\text{Saturday}}\,{ = }\left\{ {\frac{ 0. 2}{ 1} ,\,\frac{ 0. 2}{ 3} ,\,\frac{ 0. 6}{ 7}} \right\}} \\ {{\text{Thursday = }}\left\{ {\frac{ 0. 3}{ 1} ,\,\frac{ 0. 4}{ 5} ,\,\frac{ 0. 1}{ 6}} \right\}} \\ \end{array} } \right.$$

$$\begin{aligned} T\left( {\tilde{1} \ge \,\tilde{2}\,,\;\,\tilde{6}} \right)\,,\,\,T\left( {\tilde{2} \ge \,\tilde{1}\,,\;\,\tilde{6}} \right)\,,\,\,T\left( {\tilde{6} \ge \,\tilde{1}\,,\;\,\tilde{2}} \right) \hfill \\ T\left( {\tilde{1} \ge \,\tilde{2}\,,\,\tilde{6}} \right) = \hbox{min} \left\{ {0.6,\,0.4} \right\} = 0.4 \hfill \\ T\left( {\tilde{1} \ge \,\tilde{2}} \right)\,,\,\,T\left( {\tilde{1} \ge \,\,\tilde{6}} \right)\,,\;T\left( {\tilde{1} \ge \,\tilde{2}} \right)\, = 0.6\,,\; \hfill \\ T\left( {\tilde{1} \ge \,\tilde{6}} \right)\, = 0.4\, \hfill \\ T\left( {\tilde{2} \ge \,\tilde{1}\,,\,\tilde{6}} \right) = \hbox{min} \left\{ {0.2,\,0.3} \right\} = 0.2 \hfill \\ T\left( {\tilde{2} \ge \,\tilde{1}} \right) = 0.2,\;T\left( {\tilde{2} \ge \,\tilde{6}} \right) = 0.3 \hfill \\ T\left( {\tilde{6} \ge \,\tilde{1}\,,\,\;\tilde{2}} \right) = \hbox{min} \left\{ {0.2,\,0.4} \right\} = 0.2 \hfill \\ T\left( {\tilde{6} \ge \,\tilde{1}} \right) = 0.2,\;T\left( {\tilde{6} \ge \,\tilde{2}} \right) = 0.4 \hfill \\ \end{aligned}$$

$$\begin{aligned} {\text{T}}\left( {{\tilde{\text{1}}}\; \ge \;\,\tilde{2} ,\,\;{\tilde{\text{6}}}} \right){ = }\,{ \hbox{min} }\;{\text{\{ 0}} . 6 ,\; 0. 4 {\text{\} = 0}} . 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{Saturday}} \hfill \\ \left\{ \begin{aligned} {\text{T}}\left( {\widetilde{ 2}\; \ge \;\tilde{1} ,\,\;{\tilde{\text{6}}}} \right){ = }\,{ \hbox{min} }\;{\text{\{ 0}} . 2 ,\; 0. 3 {\text{\} = 0}} . 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{Saturday}} \hfill \\ {\text{T}}\left( {\widetilde{ 2\;} \ge \;\tilde{1} ,\;\,{\tilde{\text{6}}}} \right){ = }\,{ \hbox{min} }\;{\text{\{ 0}} . 2 ,\; 0. 4 {\text{\} = 0}} . 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{Sunday}} \hfill \\ \end{aligned} \right \} \hfill \\ \end{aligned}$$

Two selections have the same priority

$$\begin{array}{*{20}c} {\text{Prioritization over the daily }} \\ {{\text{timeslots of lecturer}}\;\tilde{L}_{2} } \\ \end{array} { = }\left\{ \begin{aligned} \frac{ 0. 6}{\text{Saturday}}\, ,\,\,\frac{ 0. 2}{{{\text{Sunday}}\,}} ,\, \hfill \\ \,\frac{ 0. 2}{{{\text{Thursday}}\,}} \hfill \\ \end{aligned} \right\}$$

Monday has higher priority for lecturer $\tilde{L}_{2}$.