Skip to main content
Springer Nature Link
Log in

Dynamic Sectorization - Conceptualization and Application

  • Conference paper
  • First Online:
Innovations in Mechanical Engineering II (icieng 2022)

Part of the book series: Lecture Notes in Mechanical Engineering ((LNME))

Included in the following conference series:

  • 787 Accesses

Abstract

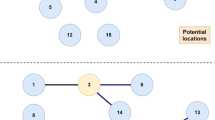
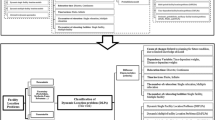
Sectorization is the division of a large area, territory or network into smaller parts considering one or more objectives. Dynamic sectorization deals with situations where it is convenient to discretize the time horizon in a certain number of periods. The decisions will not be isolated, and they will consider the past. The application areas are diverse and increasing due to uncertain times. This work proposes a conceptualization of dynamic sectorization and applies it to a distribution problem with variable demand. Furthermore, Genetic Algorithm is used to obtain solutions for the problem since it has several criteria; Analytical Hierarchy Process is used for the weighting procedure.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Bação, F., Lobo, V., Painho, M.: Applying genetic algorithms to zone design. Soft. Comput. 9, 341–348 (2005)

    Article  Google Scholar 

  2. Bozkaya, B., Erkut, E., Laporte, G.: A tabu search heuristic and adaptive memory procedure for political districting. Eur. J. Oper. Res. 144, 12–26 (2003)

    Article  Google Scholar 

  3. Kalcsics, J., Nickel, S., Schröder, M.: Towards a unified territorial design approach - applications, algorithms and GIS integration. TOP 13, 1–56 (2005). https://doi.org/10.1007/BF02578982

    Article  MathSciNet  MATH  Google Scholar 

  4. Lodish, L.: Sales territory alignment to maximize profit. J. Marketing Res. 12, 30–36 (1975)

    Article  Google Scholar 

  5. Salazar-Aguilar, A., Ríos-Mercado, R., Gonzalez-Velarde, J., Molina, J.: Multiobjective scatter search for a commercial territory design problem. Ann. Oper. Res. 199, 343–360 (2012)

    Article  MathSciNet  Google Scholar 

  6. Molina, J., Laguna, M., Marti, R., Caballero, R.: SSPMO: a scatter tabu search procedure for non-linear multiobjective optimization. INFORMS J. Comput. 19, 91–100 (2007)

    Article  MathSciNet  Google Scholar 

  7. Deb, K., Pratap, A., Agarwal, S., Meyarivan, T.: A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6(2), 182–197 (2002)

    Article  Google Scholar 

  8. Lei, H., Wang, R., Laporte, G.: Solving a multi-objective dynamic stochastic districting and routing problem with a co-evolutionary algorithm. Comput. Oper. Res. 67, 12–24 (2016)

    Article  MathSciNet  Google Scholar 

  9. Benzarti, E., Sahin, E., Dallery, Y.: Modelling approaches for the home health care districting problem. In: 8th International Conference of Modeling and Simulation-MOSIM, pp. 10–12 (2010)

    Google Scholar 

  10. Gutierrez-Gutierrez, E.V., Vidal, C.J.: A home health care districting problem in a rapid-growing city. Ingenieria y Universidad 19, 87–113 (2015)

    Article  Google Scholar 

  11. Lin, M., Chin, K.S., Ma, L., Tsui, K.L.: A comprehensive multi-objective mixed integer nonlinear programming model for an integrated elderly care service districting problem. Ann. Oper. Res. 291(1), 499–529 (2020)

    Article  MathSciNet  Google Scholar 

  12. Lei, H., Laporte, G., Liu, Y., Zhang, T.: Dynamic design of sales territories. Comput. Oper. Res. 56, 84–92 (2015)

    Article  MathSciNet  Google Scholar 

  13. Xue, G., Wang, Z., Wang, G.: Optimization of rider scheduling for a food delivery service in O2O business. J. Adv. Transp. 2021, 1–15 (2021)

    Google Scholar 

  14. Yanık, S., Kalcsics, J., Nickel, S., Bozkaya, B.: A multi-period multi-criteria districting problem applied to primary care scheme with gradual assignment. Int. Trans. Oper. Res. 26, 1676–1697 (2019)

    Article  MathSciNet  Google Scholar 

  15. Wong, C., Suresh, S., Sundararajan, N.: A rolling horizon optimization approach for dynamic airspace sectorization. IFAC J. Syst. Control 11, 100076 (2020)

    Article  Google Scholar 

  16. Sergeeva, M., Delahaye, D., Mancel, C., Vidosavljevic, A.: Dynamic airspace configuration by genetic algorithm. J. Traffic Transp. Eng. (English Edition) 4(3), 300–314 (2017). https://www.sciencedirect.com/science/article/pii/S2095756417301927

  17. Agustín-Blas, L.E., Salcedo-Sanz, S., Ortiz-García, E.G., Portilla-Figueras, A., Pérez-Bellido, Á.M.: A hybrid grouping genetic algorithm for assigning students to preferred laboratory groups. Expert Syst. Appl. 36(3), 7234–7241 (2009)

    Article  Google Scholar 

  18. Konak, A.: Network design problem with relays: a genetic algorithm with a path-based crossover and a set covering formulation. Eur. J. Oper. Res. 218(3), 829–837 (2012)

    Article  Google Scholar 

  19. Di Nardo, A., Di Natale, M., Santonastaso, G.F., Tzatchkov, V.G., Alcocer-Yamanaka, V.H.: Water network sectorization based on a genetic algorithm and minimum dissipated power paths. Water Sci. Technol. Water Supply 13(4), 951–957 (2013)

    Article  Google Scholar 

  20. Noorian, S.S., Murphy, C.E.: Balanced allocation of multi-criteria geographic areas by a genetic algorithm. In: Peterson, M.P. (ed.) ICACI 2017. LNGC, pp. 417–433. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-57336-6_29

    Chapter  Google Scholar 

  21. Saaty, T.L.: A scaling method for priorities in hierarchical structures. J. Math. Psychol. 15(3), 234–281 (1977)

    Article  MathSciNet  Google Scholar 

  22. Saaty, T.L.: How to make a decision: the analytic hierarchy process. Eur. J. Oper. Res. 48(1), 9–26 (1990)

    Article  Google Scholar 

  23. Saaty, T.L.: Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 1(1), 83–98 (2008)

    Google Scholar 

  24. Rodrigues, A.M., Ferreira, J.S.: Measures in sectorization problems. In: Barbosa Póvoa, A.P.F.D., de Miranda, J.L. (eds.) Operations Research and Big Data. SBD, vol. 15, pp. 203–211. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24154-8_24

    Chapter  Google Scholar 

  25. Goldberg, D.E., Holland, J.H.: Genetic algorithms and machine learning. Mach. Learn. 3(2), 95–99 (1988). https://doi.org/10.1023/A:1022602019183

    Article  Google Scholar 

Download references

Acknowledgments

This work is financed by the ERDF - European Regional Development Fund through the Operational Programme for Competitiveness and Internationalisation - COMPETE 2020 Programme and by National Funds through the Portuguese funding agency, FCT - Fundação para a Ciência e a Tecnologia within project ‘POCI-01-0145-FEDER-031671’.

Author information

Authors and Affiliations

  1. ISCTE - University Institute of Lisbon, Lisbon, Portugal

    Filipe Soares de Sousa & Ana Catarina Nunes

  2. CEOS.PP, ISCAP, P.PORTO, Porto, Portugal

    Maria Margarida Lima, Ana Maria Rodrigues & Cristina Oliveira

  3. INESCTEC - Technology and Science, Porto, Portugal

    Elif Göksu Öztürk, Pedro Filipe Rocha, Ana Maria Rodrigues & José Soeiro Ferreira

  4. FEUP - Faculty of Engineering, University of Porto, Porto, Portugal

    José Soeiro Ferreira

  5. FEP.UP - Faculty of Economics, University of Porto, Porto, Portugal

    Elif Göksu Öztürk

  6. CMAFcIO - Faculty of Sciences, University of Lisbon, Lisbon, Portugal

    Ana Catarina Nunes

Authors
  1. Filipe Soares de Sousa
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Maria Margarida Lima
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Elif Göksu Öztürk
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Pedro Filipe Rocha
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ana Maria Rodrigues
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. José Soeiro Ferreira
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Ana Catarina Nunes
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Cristina Oliveira
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Filipe Soares de Sousa .

Editor information

Editors and Affiliations

  1. Mechanical Engineering Department, University of Minho, Guimarães, Portugal

    José Machado

  2. Department of Industrial Electronics, University of Minho, Guimarães, Portugal

    Filomena Soares

  3. Poznan University of Technology, Poznan, Wielkopolskie, Poland

    Justyna Trojanowska

  4. Department of Civil and Mechanical Engineering, University of Cassino and Southern Lazio, Cassino, Italy

    Erika Ottaviano

  5. Faculty of Engineering, Czech University of Life Sciences Prague, Prague, Czech Republic

    Petr Valášek

  6. Faculty of Mechanical Engineering, Vellore Institute of Technology University, Vellore, India

    Mallikarjuna Reddy D.

  7. Mechanical Engineering Department, Federal University of Rio Grande do Sul, Porto Alegre, Brazil

    Eduardo André Perondi

  8. NTU "Kharkiv Polytechnic Institute", Kharkiv, Ukraine

    Yevheniia Basova

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

de Sousa, F.S. et al. (2023). Dynamic Sectorization - Conceptualization and Application. In: Machado, J., et al. Innovations in Mechanical Engineering II. icieng 2022. Lecture Notes in Mechanical Engineering. Springer, Cham. https://doi.org/10.1007/978-3-031-09382-1_26

Download citation

  • DOI: https://doi.org/10.1007/978-3-031-09382-1_26

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-031-09381-4

  • Online ISBN: 978-3-031-09382-1

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics