Abstract
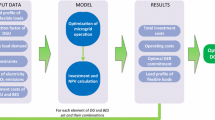
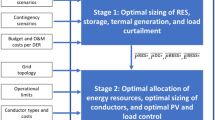
The intensification of environmental impacts and the increased economic risks are triggering a technological race towards a low-carbon economy. In this socioeconomic scenario of increasing changes and environmental concerns, microgrids (MGs) play an important role in integrating distributed energy resources. Thus, a planning strategy for grid-connected MGs with distributed energy resources and electric vehicle (EV) charging stations is proposed in this paper. The developed mathematical model aims to define MG expansion decisions that satisfy the growing electricity demand (including EV charging demand) at the lowest possible cost; such decisions include investments in PV units, wind turbines, energy storage systems, and EV charging stations. The objective function is based on the interests of the MG owner, considering constraints associated with the main distribution grid. A mixed-integer linear programming model is used to formulate the problem, ensuring the solution’s optimality. The applicability of the proposed model is evaluated in the 69-bus distribution grid. Promising results concerning grid-connected MGs were obtained, including the enhancement of energy exchange with the grid according to their needs.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Abbreviations
- \(b/u/r/w\):
-
Index of possible locations for ESS/PV/EVCS/WT units allocation.
- \(c\):
-
Index of EV charger types.
- \(g/m\):
-
Index of grid/ MG buses.
- \(i/k/h/ ij\):
-
Index of buses/circuits.
- \(M\):
-
Set of MGs.
- \({m}^{c}\):
-
Index of MG buses connected to the distribution grid.
- \(n\):
-
Index of substation buses.
- \(p/t\):
-
Index of planning periods.
- \({s/s}^{\varpi }\):
-
Index of scenarios/scenarios \(s\) contained in block \(\varpi \).
- \({\zeta }_{i}^{\mathrm{s}}\):
-
Energy emission rate supplied by grid.
- \({\eta }^{\mathrm{es}+/-}\):
-
Efficiency rate of charging and discharging for ESSs.
- \(\lambda \):
-
Number of years in each planning period.
- \({\pi }_{s}\):
-
Probability of scenarios.
- \({\varrho }_{i,p}\):
-
Apparent power demand at node \({\varvec{i}}\) and period \({\varvec{p}}\).
- \(\tau \):
-
Interest rate.
- \(\varGamma \):
-
Number of discretization blocks.
- \({C}_{c}^{\mathrm{ch}}\):
-
Cost of EV charger type \({\varvec{c}}\).
- \({C}_{s}^{\mathrm{ep}}\):
-
Cost of energy exchange between MGs and external grid at node \({\varvec{i}}\).
- \({C}_{b}^{es}\):
-
Cost of ESS.
- \({C}^{\mathrm{evcs}}\):
-
Installation cost for EVCS.
- \({C}^{\mathrm{lc}}\):
-
Cost of MG load curtailment.
- \({C}^{\mathrm{op},\mathrm{es}+}\):
-
Costs associated with ESS discharge process operation and maintenance.
- \({C}^{\mathrm{op},\mathrm{es}-}\):
-
Costs associated with ESS charge process operation and maintenance.
- \({C}^{\mathrm{op},\mathrm{pv}}\):
-
Costs associated with PV unit operation and maintenance.
- \({C}^{\mathrm{op},\mathrm{wt}}\):
-
Costs associated with WT unit operation and maintenance.
- \({C}_{u}^{\mathrm{pv}}\):
-
Cost of PV unit at bus \({\varvec{u}}\).
- \({C}_{w}^{\mathrm{wt}}\):
-
Cost of WT unit at bus \({\varvec{w}}.\)
- \({D}_{m,s,p}^{\mathrm{ev}}\):
-
EV aggregated demand, at bus \({\varvec{m}}\), scenario \({\varvec{s}},\) and period \({\varvec{p}}\).
- \({d}_{s}\):
-
Duration (hours) of scenario \({\varvec{s}}\).
- \(\overline{EM }\):
-
Maximum limit of CO2 emissions.
- \({f}_{s}^{\mathrm{D}}\):
-
Demand factor of scenario \({\varvec{s}}\).
- \({f}_{s}^{\mathrm{pv}}\):
-
PV production factor of scenario \({\varvec{s}}\).
- \({f}_{s}^{\mathrm{wt}}\):
-
WT production factor of scenario \({\varvec{s}}\).
- \({\overline{I}}_{ij}\):
-
Maximum current of circuit \({\varvec{i}}{\varvec{j}}\).
- \({l}_{ij}\):
-
Length of circuit \({\varvec{i}}{\varvec{j}}\).
- \({\overline{N}}_{c}^{\mathrm{ch}}\):
-
Maximum number of EV chargers type \({\varvec{c}}\) to be installed.
- \({\overline{N}}_{b}^{\mathrm{es}}\):
-
Maximum number of ESS to be installed at node \({\varvec{b}}\).
- \({\overline{N}}_{u}^{\mathrm{pv}}\):
-
Maximum number of PV units to be allocated at node \({\varvec{u}}\).
- \({\mathrm{P}}_{\mathrm{c}}^{\mathrm{ch}}\):
-
Capacity of EV charger type c.
- \({P}_{i,p}^{\mathrm{D}}/{Q}_{i,p}^{\mathrm{D}}\):
-
Active/reactive power demand at node i and period \({\varvec{p}}\).
- \({P}_{b}^{\mathrm{es}}\):
-
Maximum active power capacity of ESS at bus \({\varvec{b}}\).
- \({\overline{P}}_{u}^{\mathrm{pv}}\):
-
Active power capacity of PV units at bus \({\varvec{u}}\).
- \({\overline{P}}_{w}^{\mathrm{wt}}\):
-
Active power capacity of WT units at bus \({\varvec{w}}\).
- \(\overline{V}/\underline{V}\):
-
Upper and lower voltage limits.
- \({{R}^{\mathrm{L}}/X}^{\mathrm{L}}/{Z}^{\mathrm{L}}\):
-
Conductor resistance/reactance/impedance.
- \({\varrho }_{i,s,p}^{\mathrm{sqr}}\):
-
Square of the apparent power provided by the substation at bus \(i\), scenario \(s\), and period \(p.\)
- \({D}_{r,s,p}^{\mathrm{evcs}}\):
-
Charging demand in EVCS at bus \(r\), scenario s and period \(p\).
- \({I}_{ij,s,p}^{\mathrm{sqr}}\):
-
Square of current through circuit \(ij\) in scenario \(s\) and period \(p\).
- \({P}_{ij,s,p}\):
-
Active power flow through circuit \(ij\) for conductor \(a\) in scenario \(s\) and period \(p\).
- \({P}_{b,s,p}^{\mathrm{es}-/+}\):
-
Active power stored/ provided of ESS at bus \(b\), scenario \(s\), and period \(p\).
- \({P}_{m,s,p }^{\mathrm{ex}}\):
-
Active power injected/absorbed by MGs at bus \(m\), scenario \(s\), and period \(p\).
- \({P}_{m,s,p }^{\mathrm{lc}}\):
-
Active power related to load curtailment at bus \(m\), scenario \(s\), and period \(p\).
- \({P}_{u,s,p }^{\mathrm{pv}}\):
-
Active power injected by PV at node \(u\), scenario \(s\), and period \(p\).
- \({P}_{w,s,p }^{wt}\):
-
Active power injected by WT at node \(w\), scenario \(s\), and period \(p\).
- \({P}_{i,s,p}^{\mathrm{s}}\):
-
Active power supplied by substation at node \(i\), scenario \(s\), and period \(p\).
- \({Q}_{ij,s,p}\):
-
Reactive power flow through circuit \(ij\) in scenario \(\omega \) and period \(p\).
- \({Q}_{m,s,p }^{\mathrm{ex}}\):
-
Reactive power injected/absorbed by MGs at bus \(m\), scenario \(s\), and period \(p\).
- \({Q}_{m,s,p }^{\mathrm{lc}}\):
-
Reactive power related to load curtailment at bus \(m\), scenario \(s\), and period \(p\).
- \({Q}_{u,s,p}^{\mathrm{pv}}\):
-
Reactive power injected by PV at node \(u\), scenario \(s\), and period \(p\).
- \({Q}_{i,s,p}^{\mathrm{s}}\):
-
Reactive power by the substation \(i\) at node \(d\), scenario \(s\), and period \(p\)
- \({V}_{i,s,p}^{\mathrm{sqr}}\):
-
Square of the voltage at node \(i\), scenario \(s\), and period \(p\).
- \({N}_{r,c,p}^{\mathrm{ch}}\):
-
Integer variable representing the number of EV chargers at node \(r\), type \(c\) and period \(p\).
- \({N}_{b,p}^{\mathrm{es}}\):
-
Integer variable representing the number of ESS at node \(b\) and period \(p\).
- \({N}_{u,p}^{\mathrm{pv}}\):
-
Integer variable representing the number of PV units at node \(u\) and period \(p\).
- \({x}_{r,p}^{\mathrm{evcs}}\):
-
Investment variable representing the installation of an EVCS at node \(r\) and period \(p\).
- \({x}_{w,p}^{\mathrm{wt}}\):
-
Investment variable representing the installation of an WT units at node \(w\) and period \(p\).
References
United nations climate change (2019). https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement. Accessed 10 Oct 2019
IRENA: Future role of distribution system operators (2019). https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2019/Feb/IRENA_Landscape_Future_DSOs_2019.pdf?la=en&hash=EDEBEDD537DE4ED1D716F4342F2D55D890EA5B9A#:~:text=In. The future%2C DSOs will, and communication technologies (ICTs). Accessed 14 Feb 2023
Ton, D.T., Smith, M.A.: The U.S. department of energy’s microgrid initiative. Electr. J. 25, 84–94 (2012). https://doi.org/10.1016/j.tej.2012.09.013
Boloukat, M.H.S., Foroud, A.A.: Multiperiod planning of distribution networks under competitive electricity market with penetration of several microgrids, Part I: modeling and solution methodology. IEEE Trans. Ind. Inform. 14, 4884–4894 (2018). https://doi.org/10.1109/TII.2018.2807396
Hajipour, E., Bozorg, M., Fotuhi-Firuzabad, M.: Stochastic capacity expansion planning of remote microgrids with wind farms and energy storage. IEEE Trans. Sustain. Energy 6, 491–498 (2015). https://doi.org/10.1109/TSTE.2014.2376356
Zidan, A., Gabbar, H.A.: Scheduling interconnected micro energy grids with multiple fuel options. In: Smart Energy Grid Engineering, pp. 83–99. Elsevier (2017)
Hirsch, A., Parag, Y., Guerrero, J.: Microgrids: a review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 90, 402–411 (2018). https://doi.org/10.1016/j.rser.2018.03.040
Mohan, H.M., Dash, S.K.: Renewable energy-based dc microgrid with hybrid energy management system supporting electric vehicle charging system. Systems 11, 273 (2023). https://doi.org/10.3390/systems11060273
Reiz, C., De Lima, T.D., Leite, J.B., et al.: A multiobjective approach for the optimal placement of protection and control devices in distribution networks with microgrids. IEEE Access 10, 41776–41788 (2022). https://doi.org/10.1109/ACCESS.2022.3166918
Shaban Boloukat, M.H., Akbari Foroud, A.: Stochastic-based resource expansion planning for a grid-connected microgrid using interval linear programming. Energy 113, 776–787 (2016). https://doi.org/10.1016/j.energy.2016.07.099
Sun, K., Li, C., Peng, Q.: Planning of microgrid based on information gap decision theory. In: 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), pp. 144–149. IEEE (2020)
de Lima, T.D., Franco, J.F., Lezama, F., et al.: Joint optimal allocation of electric vehicle charging stations and renewable energy sources including CO2 emissions. Energy Inform. 4 (2021). https://doi.org/10.1186/s42162-021-00157-5
Bordin, C., Tomasgard, A.: SMACS model, a stochastic multihorizon approach for charging sites management, operations, design, and expansion under limited capacity conditions. J. Energy Storage 26, 100824 (2019). https://doi.org/10.1016/j.est.2019.100824
de Lima, T.D., Soares, J., Lezama, F., et al.: A Risk-based planning approach for sustainable distribution systems considering EV charging stations and carbon taxes. IEEE Trans. Sustain. Energy, 1–14 (2023). https://doi.org/10.1109/TSTE.2023.3261599
De Lima, T.D., Franco, J.F., Lezama, F., Soares, J.: A specialized long-term distribution system expansion planning method with the integration of distributed energy resources. IEEE Access 10, 19133–19148 (2022). https://doi.org/10.1109/ACCESS.2022.3146799
Baringo, L., Conejo, A.J.: Correlated wind-power production and electric load scenarios for investment decisions. Appl. Energy 101, 475–482 (2013). https://doi.org/10.1016/j.apenergy.2012.06.002
Nicholas, M.: Estimating electric vehicle charging infrastructure costs across major U.S. metropolitan areas. Int. Counc. Clean Transp. (11) (2019)
Mongird, K., Viswanathan, V., Balducci, P., et al.: Energy storage technology and cost characterization report | Department of Energy (2019)
De Lima, T.D., Reiz, C., Soares, J., et al.: Distributed energy resources and EV charging stations expansion planning for grid-connected microgrids: Study data (2023). https://docs.google.com/spreadsheets/d/1sUFRBoEwLYr47LSAD0NABv4bz0lyoJ90/edit?usp=sharing&ouid=116642585806249513780&rtpof=true&sd=true. Accessed 10 May 2023
Acknowledgments
The present work has received funding from the Brazilian Federal Agency for Support and Evaluation of Graduate Education (CAPES) and through the FCT Portuguese Foundation for Science and Technology (2019.00141.CBM). We also acknowledge the work facilities and equipment provided by GECAD research center (UIDB/00760/2020 and UIDP/00760/2020) to the project team and CEECIND/00420/2022 (Joao Soares grant). Also, the Brazilian team acknowledges the scholarships granted from the Brazilian Federal Agency for Support and Evaluation of Graduate Education (CAPES), in the scope of the Program CAPES-PrInt, process number 88887.310463/2018-00, Mobility number 88887.570741/2020-00. Moreover, was supported by other Brazilian institutions, the Brazilian National Council for Scientific and Technological Development (CNPq)-Grant No. 409359/2021-1 and the São Paulo Research Foundation (FAPESP)-grants 2015/21972-6, 2018/08008-4, and 2022/03161-4.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
de Lima, T.D., Reiz, C., Soares, J., Lezama, F., Franco, J.F., Vale, Z. (2024). Distributed Energy Resources and EV Charging Stations Expansion Planning for Grid-Connected Microgrids. In: Jørgensen, B.N., da Silva, L.C.P., Ma, Z. (eds) Energy Informatics. EI.A 2023. Lecture Notes in Computer Science, vol 14468. Springer, Cham. https://doi.org/10.1007/978-3-031-48652-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-48652-4_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-48651-7
Online ISBN: 978-3-031-48652-4
eBook Packages: Computer ScienceComputer Science (R0)