Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-24T06:28:37.999Z Has data issue: false hasContentIssue false
  • English
  • Français

On the complexity of the theories of weak direct powers

Published online by Cambridge University Press:  12 March 2014

Charles Rackoff
Charles Rackoff*
Affiliation:
University of Toronto, Toronto, Canada M55 1A7
Get access Rights & Permissions [Opens in a new window]

Abstract

Mostowski [11] shows that if a structure has a decidable theory, then its weak direct power has one as well; his proof however never produces decision procedures which are elementary recursive.

Some very general results are obtained here about the nature of the weak direct power of a structure, which in most cases lead to elementary recursive decision procedures for weak direct powers of structures which themselves have elementary recursive procedures.

In particular, it is shown that 〈N*, +〉, the weak direct power of 〈N, +〉, can be decided in space

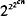
for some constant c. As corollaries, the same upper bound is obtained for the theory of the structure 〈N +, ·〉 of positive integers under multiplication, and for the theory of finite abelian groups. Fischer and Rabin [7] have shown that the theory of 〈N,* +〉 requires time

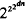
even on nondeterministic Turing machines.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 3 , September 1976 , pp. 561 - 573
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

This research was supported by the National Science Foundation under research grant GJ–34671, while the author was at the Massachusetts Institute of Technology, Project MAC and the Department of Computer Science, University of Toronto.

References

REFERENCES

[1] Cobham, A., The intrinsic computational difficulty of functions, 1964 International Congress for Logic, Methodology, and Philosophy of Science, North-Holland, Amsterdam, 1964, pp. 24n30.Google Scholar
[2] Cooper, C. D., Theorem-proving in arithmetic without multiplication, Computer and logic group memorandum No. 16, University College of Swansea, 04, 1972.Google Scholar
[3] Ehrenfeucht, A., An application of games to the completeness problem for formalized theories, Fundamenta Mathematicae, vol. 49, (1961), pp. 129–141.CrossRefGoogle Scholar
[4] Ershov, Y. L., Lavrov, I. A., Taimanov, A. D. and Taitslin, M. A., Elementary theories, Russian Mathematical Surveys, vol. 20 (1965), pp. 35–105.CrossRefGoogle Scholar
[5] Feferman, S. and Vaught, R. L., The first order properties of products of algebraic systems, Fundamenta Mathematicae, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[6] Ferrante, J. and Rackoff, C., A decision procedure for the first order theory of real addition with order, SIAM Journal for Computing, vol. 4 (1975), pp. 67–76.CrossRefGoogle Scholar
[7] Fischer, M. J. and Rabin, M. O., Super-exponential complexity of Presburger arithmetic, Complexity of real computational processes, American Mathematical Society, Providence, R. I., 1974.Google Scholar
[8] MacLane, S. and Birkhoff, G., Algebra, Macmillan, New York, 1968, 598 pp.Google Scholar
[9] Meyer, A. R., Weak monadic second order theory of successor is not elementary -recursive, Boston University Logic Colloquium Proceedings, 23 pp.Google Scholar
[10] Meyer, A. R. and Stockmeyer, L., The equivalence problem for regular expressions with squaring requires exponential space, 13th Switching and Automata Theory Symposium, IEEE, 1972, pp. 125–129.CrossRefGoogle Scholar
[11] Mostowski, A., On direct powers of theories, this Journal, vol. 17 (1952), pp. 1–31.Google Scholar
[12] Oppen, D. C., Elementary bounds for Presburger arithmetic, Sth ACM Symposium on Theory of Computing, 04 1973, 34–37.Google Scholar
[13] Péter, R., Recursive functions, Academic Press, New York, 1967, 300 pp.Google Scholar
[14] Presburger, M., Ueber die Vollständigkeit eines gewissen Systems der Arithmetik ganzer Zahlen in welchem die Addition als einzige Operation hervortritt, Comptes Rendus, I Congrès des Mathematiciens des Pays Slaves, Warsaw, 1929, 192–201, 395.Google Scholar
[15] Rackoff, C. W., The computational complexity of some logical theories, M. I. T. Project MAC Technical report 144, 1975, 130 pp.Google Scholar
[16] Ritchie, R. W., Classes of predictably computable functions, Transactions of the American Mathematical Society, vol. 106 (1963), pp. 139–173.CrossRefGoogle Scholar
[17] Stockmeyer, L. and Meyer, A. R., Word problems requiring exponential time, 5th ACM Syposium on Theory of Computing, 04, 1973, pp. 1–9.Google Scholar
[18] Szmielew, W., Elementary properties of abelian groups, Fundamenta Mathematicae, vol. 41 (1955), pp. 203–271.CrossRefGoogle Scholar