Abstract
G-quadruplexes (GQs) are topologically diverse, highly thermostable noncanonical nucleic acid structures that form in guanine-rich sequences in DNA and RNA. GQs are implicated in transcriptional and translational regulation and genome maintenance, and deleterious alterations to their structures contribute to diseases such as cancer. The expression of the B-cell lymphoma 2 (Bcl-2) anti-apoptotic protein, for example, is under transcriptional control of a GQ in the promoter of the bcl-2 gene. Modulation of the bcl-2 GQ by small-molecules is of interest for chemotherapeutic development but doing so requires knowledge of the factors driving GQ folding and stabilization. To develop a greater understanding of the electrostatic properties of the bcl-2 promoter GQ, we performed molecular dynamics simulations using the Drude-2017 polarizable force field and compare relevant outcomes to the nonpolarizable CHARMM36 force field. Our simulation outcomes highlight the importance of dipole-dipole interactions in the bcl-2 GQ, particularly during the recruitment of a bulk K+ ion to the solvent-exposed face of the tetrad stem. We also predict and characterize an “electronegative pocket” at the tetrad-long loop junction that induces local backbone conformational change and may induce local conformational changes at cellular concentrations of K+. These outcomes suggest moieties within the bcl-2 GQ can be targeted by small molecules to modulate bcl-2 GQ stability.
Graphical Abstract
INTRODUCTION
A G-quadruplex (GQ) is a type of non-canonical nucleic acid structure that can form in guanine-rich nucleic acids segments. These guanines form a tetrad core typically comprised of three layers of four guanine bases that interact via Hoogsteen hydrogen bonding1. The bases orient such that their carbonyl oxygen atoms face inward, creating an electronegative channel that is stabilized by the coordination of monovalent cations1–3. Interest in GQ structure and function has grown recently due to increasing evidence associating GQ stability with genetic disease4–7. GQs are enriched in gene promoters8,9, telomeres10, and origins of replication11–13, implicating them in modulating gene expression and genome stability. That is, the folding or unwinding of GQs may dictate whether certain biological processes, such as replication or transcription, proceed. GQ stability can also be modulated by the binding of proteins such as transcription factors. Characterizing promoter GQs is of increasing interest to researchers as their prevalence in the human genome and topological diversity make them promising therapeutic targets14–17.
The B-cell lymphoma 2 (bcl-2) gene encodes for the Bcl-2 mitochondrial protein, which functions as an inhibitor of cell apoptosis18. Overexpression of bcl-2 is associated with the growth of many types of tumors, including B-cell lymphoma19, as well as breast, prostate, cervical, colorectal, and small cell lung carcinomas20–24. Given the role of Bcl-2 in regulating cellular survival, modulating its expression with small-molecule therapeutics is a promising avenue for novel chemotherapeutic development. The bcl-2 gene is under control of two upstream promoter regions, known as P1 and P225. The nucleotide sequence upstream of the P1 promoter is GC-rich and its mutation or deletion is associated with increased promoter activity26, implying a negative regulatory role for this sequence. This GC-rich sequence has the ability to fold into a mixed parallel/antiparallel GQ structure27; however, the GQ is thought to be in equilibrium among several topologies with varying loop lengths28. The dominant structure is believed to have 1-, 3-, and 7-nucleotide (nt) loops and was resolved by Dai et al. using solution NMR spectroscopy29. A detailed understanding of the atomistic and thermodynamic factors governing this structure is integral to effective small-molecule chemotherapeutic design.
Molecular dynamics (MD) simulations can provide such atomistic insight into GQ structures, demonstrated by numerous simulation studies that have provided a greater understanding of GQ dynamics and factors influencing loop conformation. However, previous simulations have also demonstrated issues simulating GQ core hydrogen bonding30–33, core ion binding34,35 and flexible loop regions36,37, which can largely be attributed to the additive nature of the force fields used38. The absence of electronic polarization has been identified as a possible limitation in simulations of GQs30,39. In nonpolarizable FFs, charges are assigned via a mean-field approximation of electronic polarization. However, such an approach limits accuracy of the FF in cases for which electronic polarization may be particularly important, such as the GQ tetrad core34. Recently, several polarizable FFs for nucleic acids have emerged, including AMOEBA40 and Drude-201741,42, enabling new simulations investigating GQ structure and dynamics.
In the classical Drude oscillator model, electronic degrees of freedom are modeled via negatively charged auxiliary particles that are attached to parent atoms by harmonic springs. As such, movement of Drude oscillators models the reorientation of induced dipoles in response to changes in local electric fields. Such changes arise due to electrostatic interactions in the system and geometric changes within each molecule43. The Drude-2017 FF41,42,44 is based on the classical Drude oscillator model for the purpose of quantifying electronic polarization. Drude-2017 has been shown to accurately simulate duplex DNA41, DNA base flipping45, ion-DNA interactions46, as well as DNA47 and RNA GQs48. Therefore, we decided to apply the Drude-2017 FF to gain insight into the dynamics of the bcl-2 GQ.
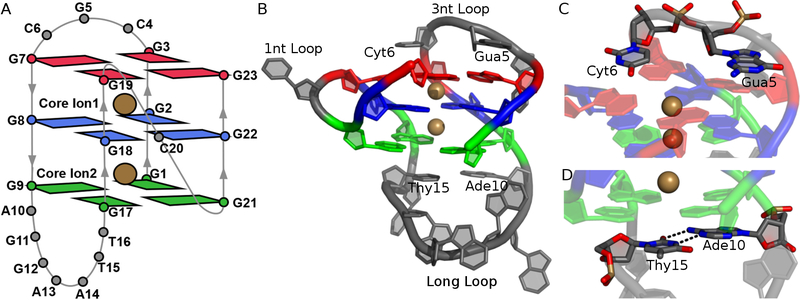
The wild-type and mutant forms of the bcl-2 GQ both adopt a mixed parallel/antiparallel topology49, including three guanine tetrads and three different intervening loop regions (Figure 1A)29. Tetrad 1 includes guanine nucleotides 3, 7, 19, and 23; tetrad 2 contains guanines 2, 8, 18, and 22, and tetrad 3 is formed by guanines 1, 9, 17, and 21. The first loop in the sequence is a 3-nt lateral loop that extends from residues 4 to 6. The second loop of the sequence is another lateral loop that comprises residues 10 to 16. This loop is seven nucleotides long, making it the longest loop in the structure. The third loop of the sequence is a 1-nt, double-chain-reversal loop between the parallel two guanine runs. GQs with loop regions of seven nucleotides in length are uncommon as longer loops tend to destabilize GQs by compromising the GQ core50. The loops of the bcl-2 GQ are arranged such that the 3-nt lateral loop is positioned above the GQ tetrad core and the long loop is below the tetrad core. The Gua5 and Cyt6 bases in the 3-nt loop stack with the bases of tetrad 1 (Figure 1C), leaving the bases of tetrad 1 exposed to solvent; we refer to this aspect of the bcl-2 structure as the “open face.” The Ade10 and Thy15 residues in the long loop stack with the bases in tetrad 3 and participate in canonical base pairing (Figure 1D), leaving tetrad 3 more occluded from the solvent than tetrad 1.
Figure 1.
Structure of the bcl-2 GQ. (A) Schematic of all residues in bcl-2 GQ structure and core ions. (B) Full structure shown in cartoon with bound K+ ions, taken from the NMR ensemble deposited in PDB entry 2F8U. Core guanine nucleotides are colored by tetrad (Tetrad 1 – red, Tetrad 2 – blue, Tetrad 3 – green). Loop regions are colored in grey. (C) Stick representation of Gua5 and Cyt6, which stack with tetrad 1. (D) Stick representation of Ade10 and Thy15, which participate canonical base pairing to stabilize the long loop below tetrad 3.
Here, we used the Drude-2017 polarizable FF to simulate the G15T/G16T double mutant form of the bcl-2 promoter GQ. This structure has been simulated previously using additive FFs51–55, but some of the simulation outcomes, such as expulsion of coordinated K+ ions in the GQ stem and bifurcated guanine hydrogen bonding, are inconsistent with known properties of GQs. Such discrepancies have been observed across different GQ simulations, suggesting FF defects or inadequate sampling. Electronic polarization is a major physical force that has been absent from many previous simulations but may be necessary for accurate GQ simulations35,38. As such, we expect the application of the Drude FF to provide greater insights into GQ structure and dynamics, towards new developments in drug discovery. We also simulated the mutated bcl-2 GQ with the CHARMM36 (C36) FF56–58 to contextualize the effects of electronic polarization and because, to our knowledge, no simulations have previously been performed on bcl-2 GQ or any mixed parallel/antiparallel GQ using CHARMM36.
METHODS
System Preparation.
The starting coordinates for all simulations were taken from the first structure in the solution NMR ensemble from Protein Data Bank entry 2F8U29. The experimental structure lacks the bound K+ that are expected in the tetrad core, so these two K+ ions were added to the structure using the CHARMM program59 by assigning their positions as the average coordinates of the carbonyl oxygen (O6) atoms of the guanine bases of consecutive tetrads. One ion was placed in between the first and second tetrads (“bound ion 1”) as well as in between the second the third tetrads (“bound ion 2”).
All systems were initially prepared using the additive C36 force field for nucleic acids56–58, CHARMM-modified TIP3P water60–62 (including Lennard-Jones terms on hydrogen bonds), and standard CHARMM ion parameters63. The bcl-2 GQ structure was centered in a cubic unit cell with a minimum box-solute distance of 10 Å, which was subsequently filled with TIP3P water and 150 mM KCl, including neutralizing counter ions. The KCl concentration of 150 mM was chosen because it is consistent with what has been validated as appropriate for GQ folding64.
Solvated systems were energy-minimized in CHARMM by performing 500 steps of steepest descent minimization and 500 steps of adopted basis Newton-Raphson minimization. After energy minimization, equilibration was performed in NAMD65 for 1 ns with position restraints applied to all non-hydrogen GQ atoms as well as the bound K+ ions using a force constant of 5 kcal mol−1 Å−2. All water molecules and mobile ions in bulk solution were allowed to diffuse freely. An NPT ensemble was implemented via the Langevin thermostat method at 298 K with a friction coefficient of 5 ps−1. The Langevin piston method66 was applied to keep the pressure at 1 atm with an oscillation period of 200 fs and a decay time of 100 fs. The box was scaled isotropically. Periodic boundary conditions were applied in all three dimensions. The particle mesh Ewald method67,68 was used to calculate electrostatic interactions with a real-space cutoff of 12 Å and a grid spacing of ~1 Å. The short-range van der Waals forces were switched to zero from 10 – 12 Å. All bonds involving hydrogen atoms were constrained using the SHAKE69 algorithm, and all water molecules were constrained with SETTLE70 which allowed for an integration timestep of 2 fs. Three independent C36 replicates were produced by generating different random velocities at the outset of equilibration.
The equilibrated C36 systems were converted to Drude in CHARMM by adding Drude oscillators and lone pairs to all non-hydrogen atoms. Doing so also converted the TIP3P water molecules to the SWM4-NDP71 polarizable water model. The Drude-2017 nucleic acid FF41,44 was applied to the GQ and the parameters of Yu et al.72, with nucleic acid-specific nonbonded interaction parameters by Savelyev and MacKerell73, were applied to monovalent ions. The Drude oscillator positions were then relaxed with steepest descent minimization and adopted basis Newton-Raphson energy minimization in CHARMM. NPT equilibration was then performed for 1 ns at 298 K and 1 atm by extended Lagrangian integration74, implemented in NAMD as Langevin dynamics45. Real atoms were coupled to a “physical” thermostat with a friction coefficient of 5 ps−1 to maintain the system temperature at 298 K. Drude oscillators were coupled to a low-temperature relative thermostat at 1 K with a friction coefficient of 20 ps−1. The short-range van der Waals potential was switched to zero from 10 – 12 Å. The harmonic position restraints and constraint scheme was the same as in the C36 systems, but the integration time-step was set to 1 fs, because Drude-atom bond vibrations are the highest frequency motions in these systems. To avoid polarization catastrophe, a “hard wall” constraint77 was applied to allow a maximum Drude-atom bond length of 0.2 Å.
Production MD Simulations.
Unrestrained simulations were performed in OpenMM,78 which has been recently extended to support the Drude oscillator model79. Three production simulations were performed for 1 μs each for a total sampling time of 3 μs with each FF. Temperature in the C36 simulations were maintained using the Andersen thermostat80 with a collision frequency of 1 ps−1. For both FFs, pressure was regulated isotropically with the Monte Carlo barostat in OpenMM with box scaling attempted every 25 integration steps. Other parameters were the same as described above during NPT equilibration in NAMD.
For reasons described below (see Results and Discussion), an additional 2 μs polarizable simulation was performed with the γ dihedral of Gua21 restrained at its value from the NMR structure (307.05°). The restraint was enforced using a harmonic restraint potential with a force constant of 1000 kcal mol−1 rad−2.
Description of Ion Binding Sites.
Ion occupancy maps were generated by discretizing the system into 1-Å3 cubic volume elements (voxels). All frames of all MD simulations were analyzed by assigning each K+ ion to the nearest voxel. The K+ ion occupancy maps were visualized with an isosurface cutoff of 1%, meaning a surface is only generated if an ion is present in a voxel for at least 1% of the total snapshots. As will be described below, bulk K+ ions tended to align with the open face of the bcl-2 GQ, along the tetrad axis. To determine the percentage of snapshots in which a bulk ion was aligned at the open face, we established a geometric criterion. The average distance between the two bound ions in the Drude simulations was 3.5 ± 0.2 Å. Using this value as a reference, we considered a bulk ion to be aligned when it was within 3.7 Å of bound ion 1, reflecting symmetry of ion alignment.
Retention of bound K+ ions in C36 simulations was evaluated by determining the percentage of snapshots in which both bound ions were present. To do so, we calculated the distance between the tetrads 1 and 3 tetrads of the first deposited NMR structure, which was 7.2 Å. Using this value as a reference, every snapshot in which two bound ions were within 3.6 Å (half of the tetrad 1 – 3 distance) of tetrad 2 was considered to have 2 bound ions, thus reflecting the symmetry of the expected ion coordination and accounting for fluctuations in the positions of the ions during the MD simulations.
RMSD-Based Clustering.
To characterize the dominant conformations from each set of simulations, clustering analysis was performed using the CHARMM clustering function81–83. These clusters were generated by pooling all replicates within a simulation set (C36 and Drude-2017), and separating frames with a maximum RMSD radius of 1.5 Å. The central structure of each cluster was subsequently used to compute pairwise RMSD between each C36 and Drude-2017 cluster following heavy-atom superposition. Doing so allowed for a quantitative comparison of the similarity between the ensembles produced by each FF.
RESULTS AND DISCUSSION
Structural Characterization and Assessment of Force Field Quality.
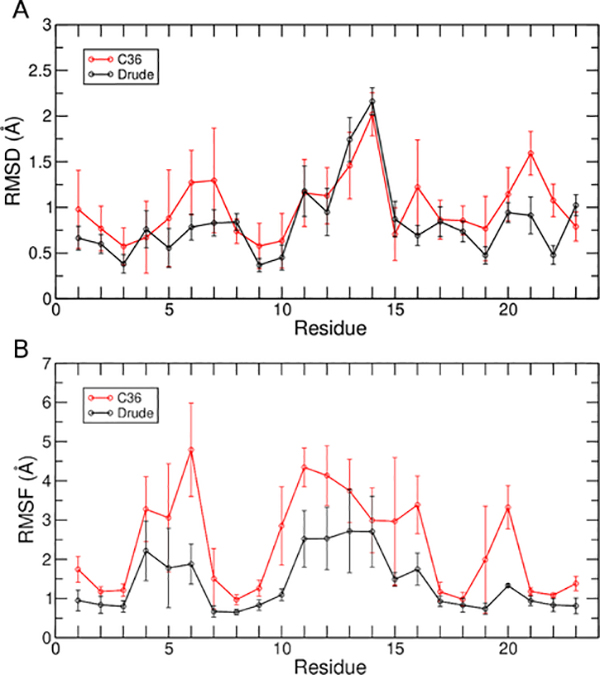
We have previously shown that the Drude-2017 FF is superior to C36 in modeling three distinct GQs in the c-kit promoter33,84, a telomeric DNA GQ, and a TERRA (RNA) GQ48. Here, we have simulated a mixed parallel/antiparallel GQ for the first time with these FFs. As such, it is important to establish the reliability of each FF in modeling this structure. To do so, we evaluated the deviation from the experimental structure with both the Drude-2017 and C36 FFs in terms of RMSD, flexibility in terms of root-mean-square fluctuation (RMSF), and compared dihedral sampling against the NMR ensemble.
RMSD was computed for all heavy atoms, guanine nucleotides in the tetrad core, and guanine base atoms in the tetrad core after performing a least-squares fit to these selected atoms. The average RMSD values for each of these structural elements in shown in Table 1. Simulations with the C36 FF yielded higher RMSD values for all selections, reflecting greater deviation from the experimental GQ structure. Conversely, simulations with the Drude-2017 FF better preserved the experimentally determined structure. To further understand the origin of the structural deviations present, the RMSD was decomposed on a per-nucleotide basis (Figure 2A). Most nucleotides had a higher RMSD in C36 simulations than those performed with Drude-2017, apart from nucleotides present in the long loop, for which similar values were obtained. These results suggest that both FFs predict long loop ensembles that deviate from the starting NMR structure by a similar extent. Such deviations are not necessarily a result of poor FF quality, as experimental evidence suggests that, in general, GQ loop regions are flexible85 and are therefore harder to resolve. Indeed, an NMR study on bcl-2 specifically determined that the long loop can adopt a wide range of conformations29.
Table 1.
Average RMSD (Å) of non-hydrogen atoms in the Drude-2017 and C36 simulations. RMSD was computed after a least-squares fit to the indicated non-hydrogen atoms of the NMR structure, taken from model 1 of the NMR ensemble. Error bars are the standard deviations of the averages over three replicate simulations with each FF.
| FF | All Nucleotides | Core Nucleotides | Core Bases |
|---|---|---|---|
| C36 | 4.9 ± 0.9 | 2.1 ± 0.6 | 1.5 ± 1.0 |
| Drude-2017 | 3.6 ± 0.8 | 1.3 ± 0.1 | 0.8 ± 0.1 |
Figure 2.
Average per-nucleotide (A) RMSD and (B) RMSF. Error bars represent the standard deviations of the averages over three replicate simulations with each FF.
To quantify the flexibility of the bcl-2 GQ with both FFs, we computed per-nucleotide RMSF (Figure 2B). In simulations performed with C36, all nucleotides of the bcl-2 GQ were more flexible than in the simulations performed with the Drude-2017 FF. Notably, the long loop, which had comparable per-nucleotide RMSD values with both FFs, was more flexible in the C36 simulations. These results suggest that with the Drude-2017 FF, the long loop adopts a more rigid conformation, deviating from the experimental starting structure but sampling a more restricted conformation ensemble than in simulations performed with the C36 FF.
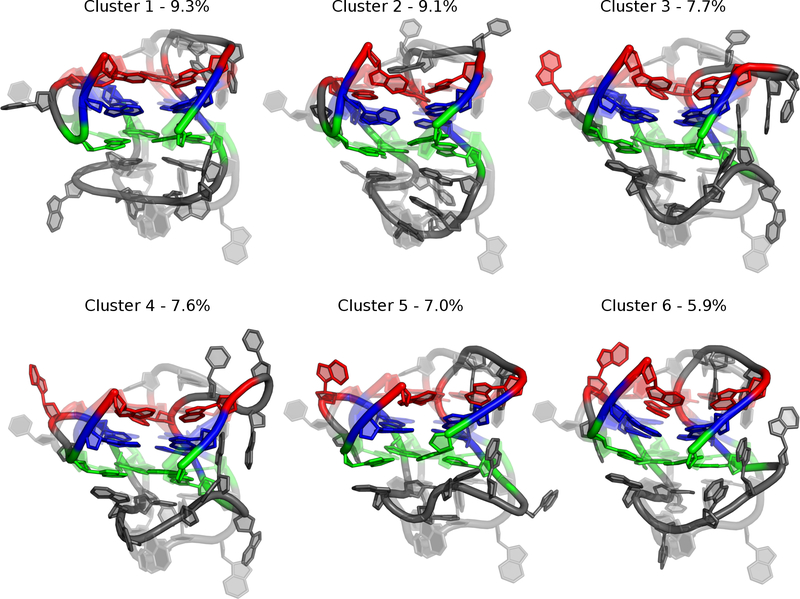
To characterize the dominant simulation conformations, we performed RMSD-based clustering of bcl-2 GQ structures collected in the simulations. The central (most representative) structures of each of the top clusters are shown in Figures 3 and 4 for the C36 and Drude-2017 simulations, respectively. The top six clusters from C36 simulations accounted for only 39% of the snapshots, reflecting a heterogeneous ensemble. Each C36 cluster differed in base orientations and backbone conformations in the three loop regions relative to the NMR structure. Specifically, most of the characteristic C36 structures lacked Gua5 and Cyt6 base stacking with tetrad 1, and none of the clusters had the expected base pairing between Ade10 and Thy15, which persisted for only 57.9% of all simulation snapshots. Both of these structural features are present in 9 of the 10 deposited structures in the NMR ensemble, and the base pairing between Ade10 and Thy15 is believed to be an important stabilizing interaction in the bcl-2 GQ long loop29. The C36 ensemble was also dominated by distorted tetrads, in which the core guanines twisted and buckled (Figure 3). This distortion is reflected in a loss of hydrogen bonding in the core, with only ~18 of the expected 24 inter-guanine hydrogen bonds preserved over time (Figure S1A). As a result, the C36 tetrads were less planar than the NMR structure, as reflected in the high RMSD values (Table 1 and Figure 2).
Figure 3.
Central structures from the C36 simulations from RMSD-based clustering of the pooled simulation trajectories. Percentages reflect the occupancy of each cluster. Guanine tetrads are colored as in Figure 1.
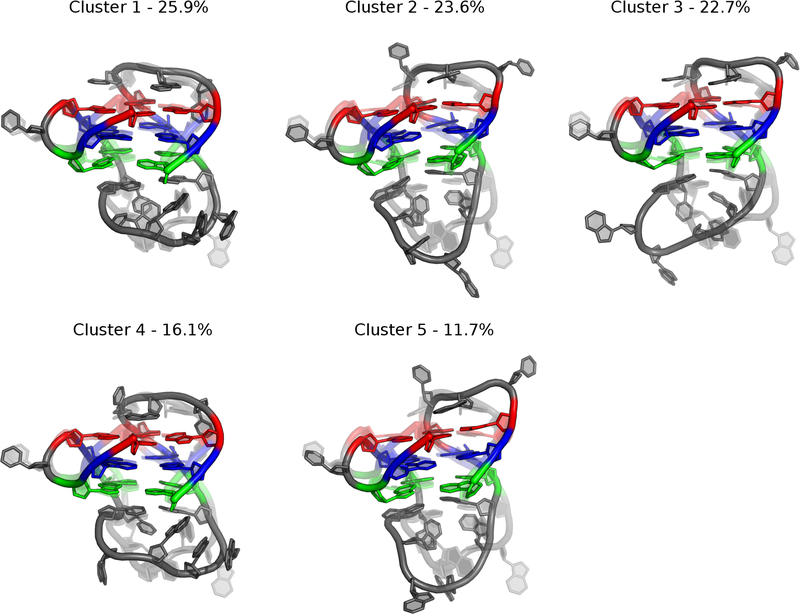
Figure 4.
Central structures from the Drude-2017 simulations from RMSD-based clustering of the pooled simulation trajectories. Percentages reflect the occupancy of each cluster. Guanine tetrads are colored as in Figure 1.
Central structures from the RMSD-based clustering of the Drude-2017 ensemble are shown in Figure 4. Five clusters were produced from the Drude-2017 simulations, representing 100% of simulation snapshots and suggesting a narrower conformational ensemble sampled in the polarizable simulations relative to simulations performed with the nonpolarizable C36 FF. These central structures all exhibit base stacking of Gua5 with tetrad 1 and two clusters show stacking of Cyt6 with tetrad 1. All clusters also feature the canonical Ade10:Thy15 base pair, which was present in 100% of snapshots in the Drude-2017 simulations. Unlike the C36 simulations, there was no twisting of tetrad guanine bases and the 24 expected hydrogen bonds in the GQ core were preserved over time, with minor fluctuations (Figure S1B).
To assess the similarity between the C36 and Drude ensembles, we computed the pairwise RMSD between the central structures of each of the top clusters produced using each FF. These values were all greater than 4.8 Å, with a maximum value of 7.1 Å (Table S1). These outcomes indicate that the ensembles produced by the C36 and Drude FFs exhibit little overlap. Still, given the lower RMSD relative to the starting NMR structure and preservation of important secondary structural features, our results suggest that the simulated ensemble produced by the Drude-2017 FF is more consistent with the experimental structure of the bcl-2 GQ than the ensemble produced by the C36 FF. As such, the remainder of our analysis will focus on the results of Drude-2017 simulations, with some comparisons to the C36 simulations when it is particularly important to highlight differences.
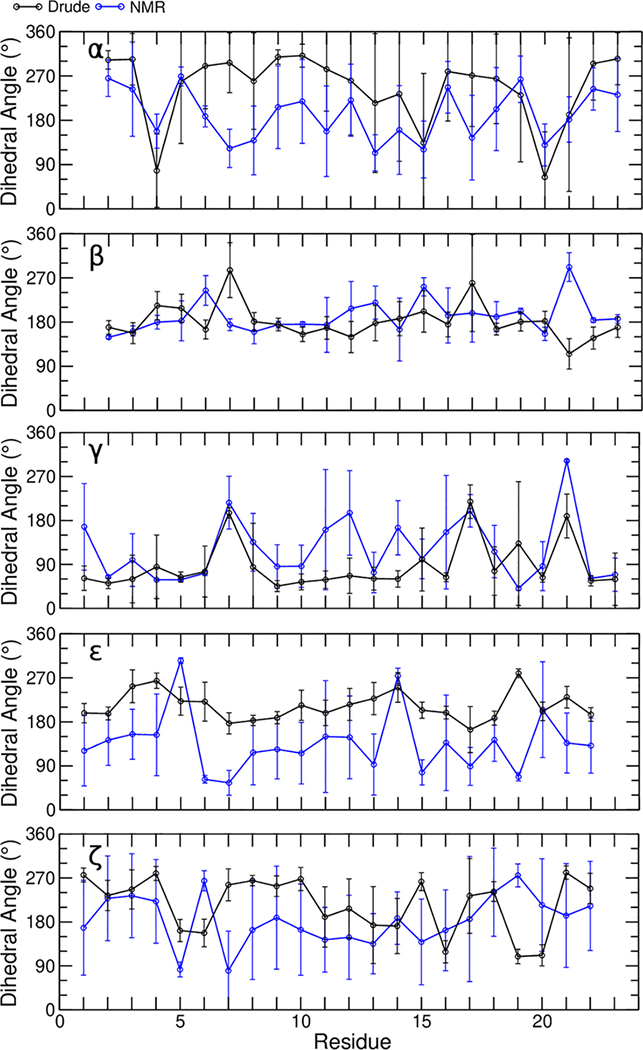
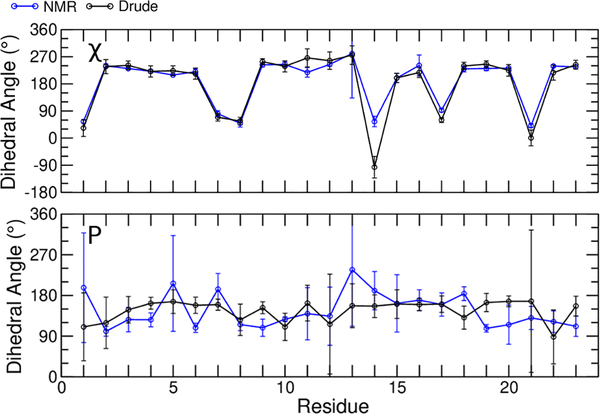
Having investigated the global structural properties of the bcl-2 GQ with both FFs, we further evaluated the sampling of backbone dihedral angles (α, β, γ, ε, and ζ, Figure 5) as well as the glyosidic torsion (χ), and sugar pseudorotation angle (P) of each nucleotide with the Drude-2017 FF (Figure 6). The results of the same calculations with the C36 FF are given in the Figures S2 and S3. In general, both FFs sampled dihedrals that agreed with the NMR ensemble, though some discrepancies were observed among the α, γ, ε, and ζ dihedrals. The β dihedral, which features large intrinsic energy barriers to rotation44, was modeled well by both FFs. Similarly, sugar puckering, which generally exhibited values South of the pseudorotation angle, was modeled as expected for DNA.
Figure 5.
Average dihedral values for backbone dihedral angles of all residues. Error bars represent the standard deviation of the 10 models in the experimental NMR ensemble and the RMSF over all data points in the pooled MD trajectories using the Drude-2017 FF.
Figure 6.
Average dihedral values for glycosidic linkage (χ) and pseudorotation angles for all residues. Error bars represent the standard deviation of the 10 models in the experimental NMR ensemble and the RMSF over all data points in the pooled MD trajectories using the Drude-2017 FF.
Evaluating the α dihedral sampling in the bcl-2 GQ is interesting because the NMR ensembles reports trans values (~180°) to many of the nucleotides while α dihedrals in canonical DNA typically samples gauche− states (300°). The prevalence of trans α dihedrals in the bcl-2 GQ suggests local backbone structure that is reminiscent of left-handed Z-DNA, specifically ZI (209°) and ZII (169°) substrates. Quantum mechanical (QM) calculations of α dihedral rotation in model compounds have shown shallow minima in the regions ZI and ZII substrates of Z-DNA, but not in A- or B-form DNA44. Though the C36 and Drude-2017 FFs both sampled α values that were systematically higher than those in the experimental ensemble, the NMR ensemble exhibits a wide range of α dihedral values at each nucleotide (Figures 5 and S2) and both FFs produced values that were generally within error of the experimental ensemble, demonstrating reasonable dihedral sampling. We cannot, however, discount the possibility of some FF bias toward canonical geometries with respect to the α dihedrals terms. A more specific refinement, one that uses full nucleotides as model compounds, may improve modeling of this torsion.
The γ dihedrals in the bcl-2 GQ NMR ensemble are distributed primarily between gauche+ and trans values (Figure 5). The gauche+ geometry is the dominant state in duplex DNA and achieving balance between gauche+ and trans is a challenge for FF development. In the AMBER ff99 parameter set, duplex DNA was unstable due to a conversion of γ dihedrals to trans, which was fixed by suppressing the trans state in the bsc0 revision of this force field86. We have previously shown that the Drude-2017 FF captures the intrinsic potential energy surface of γ rotation very well with respect to QM target data44. In simulations performed with the C36 FF, γ sampled exclusively gauche+ configurations, whereas simulations with Drude-2017 yielded better agreement at nucleotides Gua7, Gua17, Gua21. Gua7 and Gua17 both have trans γ according to the NMR structure, while Gua21 has γ in a gauche− configuration. Drude-2017 simulations did not sample gauche− states at Gua21 but modeled γ as trans. The reasons for this difference in configuration will be discussed below in the context of χ dihedrals. Loop nucleotides Gua11, Gua12 and Ade14 are assigned trans γ in the NMR ensemble but were modeled as gauche+ by both FFs.
The ε and ζ dihedral angles of DNA have tightly coupled dynamics and generally low potential energy barriers between minima44, allowing then to access a range of geometries. As such, the NMR ensemble displays a wide range of values for each of these dihedrals across all nucleotides (Figure 5). Both the C36 and Drude-2017 FFs produced ε dihedral values that were systematically higher than those of the experimental ensemble, which fell between gauche+ and trans. The simulations displayed ε values that fell in the range of canonical BI- and BII-DNA (183 – 245°)87. Values of ζ were generally in good agreement, given the large error bars associated with the experimental data (Figure 5).
The orientation of a nucleobase relative to its sugar can be described by the glycosidic linkage dihedral (χ). In a mixed parallel/antiparallel GQ, guanine bases will adopt both syn and anti orientations to form the expected 24 Hoogsteen hydrogen bonds in spite of the different directionality of the oligonucleotide chain. In the bcl-2 GQ, guanine bases 1, 7, 8, 14, 17, and 21 are all syn, with all but Gua14 (which resides in a loop) residing in the tetrad core. All other nucleobases are in the canonical anti orientation in the NMR ensemble and were modeled as such by both FFs. Both FFs modeled χ conformations well (Figures 6 and S3), but only the Drude FF preserved the expected hydrogen bonding (Figure S1).
It is important to acknowledge the difficulty in directly comparing the dihedral ensembles from the simulations to those obtained directly from the NMR ensemble. There is uncertainty in the dihedral assignments derived from the NMR data and converging the dynamics of flexible regions in structures like GQs is challenging for MD simulations. The comparison to the NMR ensemble we present here is our best effort to confirm the agreement between the simulation outcomes with experimental evidence, however we acknowledge that the NMR ensemble contains no information about the relative populations of each conformer and the kinetics of interconversion among them. A recent study by Islam et al. has explored these concepts in the context of lateral and diagonal loops in telomeric GQs,88 finding that extensive simulations can reasonably represent ensembles of such species. However, challenges remain in assessing the quality of simulations relative to NMR without a direct comparison to primary data.
K+ Ion Retention in the GQ Stem and Bulk Ion Binding.
Ion interaction maps were generated to characterize the preferred sites of K+ occupancy around the bcl-2 GQ in the Drude-2017 simulations (Figure 7). We have previously shown that C36 simulations of c-kit1, c-kit2, and telomeric GQs result in expulsion of bound K+ from the core, whereas inclusion of electronic polarization via the Drude-2017 FF leads to correct ion retention33,47,48. We have also observed the ability of different GQs to bind K+ ions from the bulk solution to the solvent-accessible faces of the tetrad core. Here, we sought to determine if these phenomena are also observed in the case of the mixed parallel/antiparallel bcl-2 GQ.
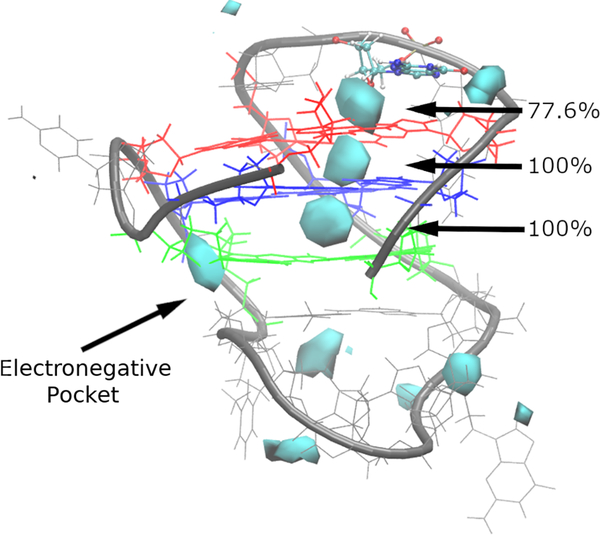
Figure 7.
Ion interaction maps indicating the K+ sampling around the bcl-2 GQ, using the NMR structure for reference with the Drude FF at an occupancy threshold of ≥1%. The Gua5 residue just above the tetrad core is shown in ball-and-stick for perspective. Guanine tetrads are colored as in Figure 1. Percentages indicate the occupancy of the three K+ binding sites along the GQ stem axis described in the main text.
In the C36 simulations, the bcl-2 GQ only retained one bound K+ ion (Figure S4), which is consistent with our previous findings on other DNA GQs using the C36 FF. Interestingly, ion expulsion followed different patterns, with bound ion 1 being expelled through tetrad 1 in two replicates and bound ion 2 expelled through tetrad 3 in the other simulation. The ion occupancy maps of individual replicate simulations are shown in Figure S5. Thus, the inability of the C36 FF to model ion retention appears to extend to the mixed parallel/antiparallel bcl-2 GQ and thus is intrinsic to the FF and is not determined by GQ topology.
In the Drude-2017 simulations, however, both bound ions were retained for the entire simulation time, across three independent replicates, leading to 100% occupancy of the expected occupancy sites in the tetrad core (Figure 7), demonstrating that the application of a polarizable FF improves descriptions of core-ion interactions in the GQ. The ion occupancy maps also reveal differences in preferred locations of K+ ions. In the polarizable simulations, we observed three distinct ion binding locations in the GQ core. Two of these locations are the expected ion binding sites between tetrads (bipyramidal antiprismatic coordination, see Figure 1), while the third binding location is at the open face of the tetrad core aligned with the GQ tetrad axis. At this third location, the Drude ion occupancy map features prominent sampling (77.6% of total simulation time). In contrast, no ion sampling was observed at this location in C36 simulations (Figure 7).
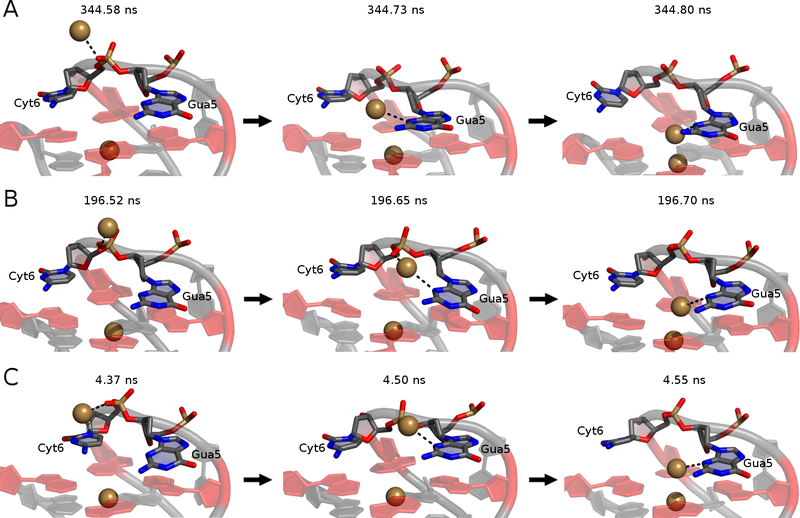
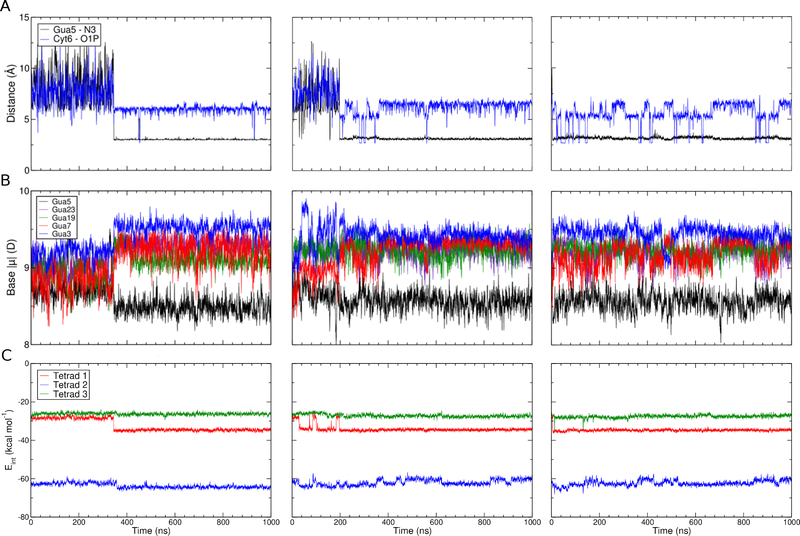
The mechanism of bulk K+ alignment at the open face is illustrated in Figure 8. Gua5 and Cyt6 both act in coordinating this bulk K+ ion at different times to facilitate coordination at the open face, along the tetrad axis. In all simulations, the bulk ion initially interacted with a non-bridging phosphate oxygen atom (O1P) in Cyt6 before interacting with both this O1P atom and the N3 atom of the Gua5 base. The K+:O1P interaction was lost, followed by the movement of Gua5 toward tetrad 1 such that the ion was finally aligned along the GQ stem. This mechanism was observed in all replicates (though at different times, as indicated by the snapshots in Figure 8) and once bound, the K+ ion never dissociated in any simulation. In replicate 2, the bulk K+ ion was briefly aligned by the N3 atom of the Cyt6 base prior to coordination by Gua5 (Figure S6). After the bulk ion dissociated from Cyt6 at ~200ns, Gua5 stacked with the tetrad core and coordinated the bulk K+ ion for the remainder of the simulation (Figure 8B).
Figure 8.
The mechanism of bulk K+ alignment. Trajectory snapshots are shown from (A) replicate 1, (B) replicate 2, and (C) replicate 3. Time stamps are indicated above each snapshot. Guanine bases in tetrad 1 are colored in red for perspective.
The persistence of this K+ coordination by a non-tetrad guanine stands in contrast to our previous observations of bulk K+ binding to the c-kit1, c-kit2, and c-kit* GQs, which was reversible on the sub-μs time scale33,47. K+ coordination in the c-kit GQs was mediated by thymine, cytosine, and guanine bases, indicating that different nucleobases can coordinate K+. Here, the observation of persistent guanine-mediated K+ alignment to the tetrad stem (irreversible on the μs time scale) of the bcl-2 GQ suggests that the sequence and architecture of the bcl-2 GQ may impact the ability of this guanine base to more stably coordinate a K+ ion. Thus, each of these GQs may have distinct electrostatic surface properties that modulate binding to ions, transcription factors, and other cellular macromolecules and that could be exploited for high-specificity small-molecule drug design to modulate these interactions and ultimately, the stability of the GQs themselves.
We also observed K+ binding in an electronegative pocket at the junction between tetrad 3 and the backbone on the long loop (Figure 7). This pocket comprises the O4’ atoms of Gua21 and Thy15, as well as the O1P atom of Thy15 (Figure S7). In two of the three simulations, a K+ ion bound in this location for the majority of the simulation time, beginning at 340 ns and 75 ns, respectively, without dissociating (Figure S8). In replicate 1, binding was transient at the beginning of the simulation but did not persist (Figure S8). Close contact between a K+ ion and the electronegative pocket atoms was accompanied by changes in the α and γ dihedrals of Gua21 (Figure S8). The experimentally assigned states of Gua21 α and γ from the NMR ensemble are gauche− (~300°) and in our simulations, these dihedrals oscillated between gauche− and gauche+ before any ions interacted with electronegative pocket atoms. In replicate 1, a K+ ion briefly bound in the electronegative pocket when both α and γ were gauche+, but the ion quickly dissociated and both dihedrals returned to predominantly gauche− conformations. In replicates 2 and 3, K+ binding was accompanied by the adoption of gauche+ conformations that quickly reverted back to gauche− in the case of Gua21 α and trans in the case of Gua21 γ (Figures S8B,C). Thus, the electronegative pocket persisted with Gua21 γ in a trans state for the remainder of the simulations, suggesting that this geometry is capable of stably coordinating a K+ ion. These conformational changes did not perturb tetrad hydrogen bonding (Figure S1B), suggesting that any ion-induced effects were confined to the phosphodiester backbone. Additionally, these conformational changes and ion binding do not revert in replicates 2 and 3, suggesting that K+ dissociation from the electronegative pocket may only be accessible at longer time scales.
There are several explanations for these differences in conformational change and why a K+ ion bound in this electronegative pocket: (1) the ion induces a conformational change, (2) the conformational change is an intrinsic fluctuation in the structure that captures the ion, or (3) there is a FF defect that causes the backbone to distort. To test the dependence of ion binding on backbone geometry, we performed an additional simulation of the bcl-2 GQ with the γ dihedral of Gua21 restrained at its value from the starting NMR structure. No K+ bound in the electronegative pocket in the restrained simulation, indicating that the conformational change from gauche to trans is needed for the electronegative pocket to form.
We characterized the electronegative pocket in the restrained and unrestrained simulations by measuring the Gua21(O4’)-Thy15(O4’) and Gua21(O4’)-Thy15(O1P) distances and plotting them as a two-dimensional free energy surface after Boltzmann weighting (Figure S9). The unrestrained ensemble exhibits a well-defined free energy minimum around Gua21(O4’)-Thy15(O1P) ~5 Å and Gua21(O4’)-Thy15(O4’) ~6 Å. These short distances indicate the formation of the compact geometry that coordinates a K+ ion. The free energy surface obtained from the single, 2-μs restrained simulation was much broader, reflecting a wide range of values for each of these distances. Therefore, the results of the restrained simulations indicate that the electronegative pocket is only stabilized in the event of Gua21 γ transition from gauche− to trans. The same analysis was performed on a per-replicate basis (Figure S10), which shows that replicate 1 produced a broad free energy minimum, similar to the restrained simulation. This outcome indicates that in the absence of a bound K+ ion, our simulations were compatible with the structures present in the NMR ensemble.
Given the variability in backbone dihedral sampling as a function of K+ binding, it is possible that K+ ions are responsible for inducing the observed backbone conformational change in the electronegative pocket. The total K+ ion concentration in the buffer used to solve the NMR structure was 60 mM (20 mM K-phosphate and 40 mM KCl)29 and our simulations contained 150 mM KCl. The increased ionic strength may induce or stabilize subtle conformational changes such as those observed in our unbiased simulations. K+ binding to electronegative pocket oxygen atoms was coupled with a gauche− to gauche+ conformational change in both Gua21 α and γ, however the gauche+ state was sampled prior to ion binding (Figure S8). These observations suggest that α and γ conformational fluctuations are intrinsic to this region of the bcl-2 GQ and K+ binding stabilizes alternate conformations and subsequently facilitates the conversion of Gua21 γ to trans with Gua21 α returning to its expected gauche− conformation. A more systematic analysis of different K+ concentrations and perhaps different monovalent cations would be required to further understand the likelihood of ion-induced conformational shifts in the bcl-2 GQ and if this property is somehow unique to K+.
Electronic Properties of GQ Nucleobases.
In the c-kit1 GQ, the binding of a bulk K+ ion strengthened the interaction energy between core K+ ions and their coordinating guanine bases, while simultaneously altering the dipole moments of guanine bases in the tetrads47. As such, we concluded that dipole-dipole interactions among K+ ions contribute to the binding strength in the tetrad core. To determine if this phenomenon extends to the bcl-2 GQ, a structure with a different fold and strong guanine coordination of a bulk K+ ion, we calculated guanine base dipole moments in tetrad 1 and the interaction energy between core K+ ion and tetrad bases over time.
Bulk K+ ion binding was monitored by the calculating the distance between the ion and either the O1P atom of Cyt6 or the N3 of Gua5 (Figure 9A), reflecting the binding mechanism described above. A sharp transition was observed in all three replicate simulations, corresponding to the movement of the K+ ion from the O1P atom of Cyt6 to the N3 atom of Gua5. The brief coordination of a K+ ion to the N3 atom of Cyt6 is not reflected in these plots but the consistency of the outcomes shown in Figure 9 confirms that this transient interaction does not alter the dominant binding mechanism. In two simulations, binding of the bulk K+ ion occurred on the order of 200 – 300 ns, but in the other simulation it was nearly instantaneous, occurring within 5 ns.
Figure 9.
Changes in base dipole moments and interaction energies in response to bulk K+ alignment. (A) Minimum distance between any bulk K+ ion and Gua5 N3 (black) and Cyt6 O1P (blue), (B) dipole moment of all guanine bases in tetrad 1 and Gua5, and (C) interaction energy between tetrad bases and K+ bound ions shown as a running average. All data series are shown as a 100-point running average.
Next, we sought to establish whether the binding of this bulk K+ ion perturbs the electronic structure of nearby guanine bases and impacts dipole-dipole interactions among the bound K+ ions in the GQ stem. The dipole moments of all tetrad 1 guanine bases and Gua5 are shown in Figure 9B, and the interaction energy between tetrad guanine bases and the bound K+ ions is shown in Figure 9C. Gua5 was included in the dipole moment analysis because it participates in bulk ion coordination above the open face, we anticipated that its electronic properties would vary as a function of ion coordination. Our analysis shows a clear relationship between tetrad guanine base dipole moment and interaction energy, as a function of bulk ion coordination. Upon coordination of the bulk K+ to the N3 of Gua5 and alignment of this along the GQ tetrad stem, base dipole moments in tetrad 1 guanine bases simultaneously increased (Figure 9B and Table 2). The magnitude of this change in dipole moment was generally on the order of 0.2 D (Table 2). At the same time, the interaction energy between bound K+ ions and guanine bases in tetrad 1 became stronger (Figure 9C and Table 3), on the order of 4 kcal mol−1. The strengthening of interaction energy is observed in tetrads 2 and 3, but to a lesser extent, less than 1 kcal mol−1 (Table 3). These results suggest strong dipole-dipole interactions propagate along the tetrad stem but are most pronounced in the closest group of guanine bases, in tetrad 1, thus dissipating as a function of distance away from the open face, as expected.
Table 2.
Average dipole moments (D) of tetrad 1 guanine bases and Gua5. Error bars are the RMSF of the pooled time series. “Aligned to Tetrad Stem” refers to frames in which a bulk K+ ion was coordinated by the N3 atom of Gua5, and “Not Aligned to Tetrad Stem” are the remaining frames. Δ|μ| is the change in base dipole moment (D), defined as (Aligned – Not Aligned).
| Aligned to Tetrad Stem | Not Aligned to Tetrad Stem | Δ|μ| | |
|---|---|---|---|
| Guanine 3 | 9.5 ± 0.4 | 9.3 ± 0.5 | 0.2 ± 0.6 |
| Guanine 7 | 9.2 ± 0.5 | 9.0 ± 0.5 | 0.2 ± 0.7 |
| Guanine 19 | 9.2 ± 0.5 | 9.0 ± 0.5 | 0.2 ± 0.7 |
| Guanine 23 | 9.2 ± 0.5 | 9.1 ± 0.5 | 0.1 ± 0.7 |
| Guanine 5 | 8.6 ± 0.6 | 8.7 ± 0.6 | −0.1 ± 0.8 |
Table 3.
Average interaction energies (kcal mol−1) between tetrad guanine bases and bound K+ ions in the stem. Error bars are the RMSF of the pooled time series. “Aligned to Tetrad Stem” refers to frames in which a bulk K+ ion was coordinated by the N3 atom of Gua5, and “Not Aligned to Tetrad Stem” are the remaining frames. ΔEINT is the change in interaction energy (kcal mol−1), defined as (Aligned – Not Aligned).
| Aligned to Tetrad Stem | Not Aligned to Tetrad Stem | ΔEINT | |
|---|---|---|---|
| Tetrad 1 | −34.9 ± 2.8 | −30.5 ± 4.2 | −4.4 ± 5.0 |
| Tetrad 2 | −62.8 ± 5.0 | −62.2 ± 4.6 | −0.6 ± 6.8 |
| Tetrad 3 | −27.2 ± 4.7 | −26.6 ± 4.4 | −0.6 ± 6.4 |
The base dipole moment of Gua5 was systematically lower than the bases in the tetrads, despite being responsible for coordinating the bulk K+ ion, which we expected to polarize the base. This observation held true regardless of whether Gua5 was directly coordinating the K+ ion, and the base even slightly depolarized upon aligning the K+ ion with the tetrad stem, though the difference was very small relative to the estimated error (Table 2). The difference in behavior observed in tetrad guanine bases and the and non-tetrad Gua5 base emphasizes the sensitivity of these bases to their electronic environments. The combined effects of Hoogsteen hydrogen bonding, coordination of K+ ions, and base stacking clearly lead to polarization of tetrad guanine bases relative to solvent-exposed guanine bases (like Gua5) or those found in duplex DNA47. Moreover, these bases are sensitive to further induced dipole effects upon alignment of another K+ ion to the open face of tetrad 1, whereas Gua5 appears to be insensitive to the proximity of K+ ions. Together, these findings emphasize the magnitude of the multibody effects that dictate the properties of tetrad guanine bases, in terms of both their base dipole moments, and their interaction energies with coordinated K+ ions.
CONCLUSIONS
Here, we have assessed the ability of the C36 and Drude-2017 FFs to model a mixed parallel/antiparallel DNA GQ, bcl-2. We have demonstrated that the Drude-2017 FF more accurately models the bcl-2 GQ in terms of reduced deviation from the experimental structure, maintenance of key base-pairing interactions that stabilize the fold, and improved cation coordination in the tetrad. Our polarizable simulations revealed two instances of ion-induced localized conformational change. A K+ ion was coordinated by Gua5, which subsequently stacked with the open face of tetrad 1, aligning the ion with the tetrad axis. We also propose the existence of an “electronegative pocket” at the tetrad-long loop junction, in which a K+ ion binds to cause a conformational change in the backbone of Gua21. These findings expand our understanding of the mechanisms by which DNA GQs may attract bulk ions and the effects these ion-binding events may have on modulating GQ structure. As we have seen previously in simulations of other DNA GQs, bulk ion alignment to the open face of the bcl-2 GQ tetrads increased the strength of interaction energy between bound ions in the tetrad stem via dipole-dipole interactions. These results highlight the critical role that dipole-dipole interactions play in governing GQ biophysical properties as well as the importance of employing polarizable simulations in the investigation of GQs. Together, our findings contribute to a greater understanding of the biochemical and biophysical properties of the bcl-2 GQ, its affinity for K+ ions, and the role that K+ ions may play in causing local conformational changes. Such observations are important for future drug design efforts against this potential chemotherapeutic target.
Supplementary Material
ACKNOWLEDGMENTS
The authors thank Danielle L. Porier for contributions in the initial stages of this project. Computing time and resources were provided by Virginia Tech Advanced Research Computing.
FUNDING INFORMATION
This work was supported by the National Institutes of Health (grant R35GM133754), the Thomas F. and Kate Miller Jeffress Memorial Trust (Bank of America, Trustee), USDA-NIFA (project number VA-160092), The American Association of University Women (American Dissertation Fellowship), and startup funding from the Virginia Tech Office of the Provost, College of Agriculture and Life Sciences, and Department of Biochemistry.
Footnotes
SUPPORTING INFORMATION AVAILABLE
Tetrad hydrogen bonding for C36 and Drude FFs; dihedral analysis for C36 simulations; ion occupancy maps for C36 simulations and for each replicate of C36 and Drude simulations; snapshots of K+ binding to Cyt6 at the open face; structural definition of the electronegative pocket; distance and dihedral time series data for K+ binding to the electronegative pocket; free energy surfaces of characteristic distances in the electronegative pocket for unrestrained and restrained simulations; pairwise RMSD between central structures in the C36 and Drude simulation clusters.
REFERENCES
- (1).Burge S; Parkinson GN; Hazel P; Todd AK; Neidle S Quadruplex DNA: Sequence, Topology and Structure. Nucleic Acids Res. 2006, 34 (19), 5402–5415. 10.1093/nar/gkl655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Gray RD; Chaires JB Kinetics and Mechanism of K+ and Na+-Induced Folding of Models of Human Telomeric DNA into G-Quadruplex Structures. Nucleic Acids Res. 2008, 36 (12), 4191–4203. 10.1093/nar/gkn379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Bhattacharyya D; Mirihana Arachchilage G; Basu S Metal Cations in G-Quadruplex Folding and Stability. Front. Chem. 2016, 4 (September), 1–14. 10.3389/fchem.2016.00038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Cammas A; Millevoi S RNA G-Quadruplexes: Emerging Mechanisms in Disease. Nucleic Acids Res. 2017, 45 (4), 1584–1595. 10.1093/nar/gkw1280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Phan AT; Kuryavyi V; Darnell JC; Serganov A; Majumdar A; Ilin S; Raslin T; Polonskaia A; Chen C; Clain D; Darnell RB; Patel DJ Structure-Function Studies of FMRP RGG Peptide Recognition of an RNA Duplex-Quadruplex Junction. Nat. Struct. Mol. Biol. 2011, 18 (7), 796–804. 10.1038/nsmb.2064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Phatak P; Cookson JC; Dai F; Smith V; Gartenhaus RB; Stevens MFG; Burger AM Telomere Uncapping by the G-Quadruplex Ligand RHPS4 Inhibits Clonogenic Tumour Cell Growth in Vitro and in Vivo Consistent with a Cancer Stem Cell Targeting Mechanism. Br. J. Cancer 2007, 96 (8), 1223–1233. 10.1038/sj.bjc.6603691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Maizels N Genomic Stability: FANCJ-Dependent G4 DNA Repair. Curr. Biol. 2008, 18 (14), 613–614. 10.1016/j.cub.2008.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Wu Y; Shin-ya K; Brosh RM FANCJ Helicase Defective in Fanconia Anemia and Breast Cancer Unwinds G-Quadruplex DNA To Defend Genomic Stability. Mol. Cell. Biol. 2008, 28 (12), 4116–4128. 10.1128/mcb.02210-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Duxin JP; Dao B; Martinsson P; Rajala N; Guittat L; Campbell JL; Spelbrink JN; Stewart SA Human Dna2 Is a Nuclear and Mitochondrial DNA Maintenance Protein. Mol. Cell. Biol. 2009, 29 (15), 4274–4282. 10.1128/mcb.01834-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Moye AL; Porter KC; Cohen SB; Phan T; Zyner KG; Sasaki N; Lovrecz GO; Beck JL; Bryan TM Telomeric G-Quadruplexes Are a Substrate and Site of Localization for Human Telomerase. Nat. Commun. 2015, 6 (May). 10.1038/ncomms8643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Zheng KW; Xiao S; Liu JQ; Zhang JY; Hao YH; Tan Z Co-Transcriptional Formation of DNA: RNA Hybrid G-Quadruplex and Potential Function as Constitutional Cis Element for Transcription Control. Nucleic Acids Res. 2013, 41 (10), 5533–5541. 10.1093/nar/gkt264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Millevoi S; Moine H; Vagner S G-Quadruplexes in RNA Biology. Wiley Interdiscip. Rev. RNA 2012, 3 (4), 495–507. 10.1002/wrna.1113. [DOI] [PubMed] [Google Scholar]
- (13).Song J; Perreault J-P; Topisirovic I; Richard S RNA G-Quadruplexes and Their Potential Regulatory Roles in Translation. Translation 2016, 4 (2), e1244031 10.1080/21690731.2016.1244031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Hurley LH; Wheelhouse RT; Sun D; Kerwin SM; Salazar M; Fedoroff OY; Han FX; Han H; Izbicka E; Von Hoff DD G-Quadruplexes as Targets for Drug Design. Pharmacol. Ther. 2000, 85 (3), 141–158. 10.1016/S0163-7258(99)00068-6. [DOI] [PubMed] [Google Scholar]
- (15).Cao Q; Li Y; Freisinger E; Qin PZ; Sigel RKO; Mao ZW G-Quadruplex DNA Targeted Metal Complexes Acting as Potential Anticancer Drugs. Inorg. Chem. Front. 2017, 4 (1), 10–32. 10.1039/c6qi00300a. [DOI] [Google Scholar]
- (16).González V; Guo K; Hurley L; Sun D Identification and Characterization of Nucleolin as a C-Myc G-Quadruplex-Binding Protein. J. Biol. Chem. 2009, 284 (35), 23622–23635. 10.1074/jbc.M109.018028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Paeschke K; Simonsson T; Postberg J; Rhodes D; Lipps HJ Telomere End-Binding Proteins Control the Formation of G-Quadruplex DNA Structures in Vivo. Nat. Struct. Mol. Biol. 2005, 12 (10), 847–854. 10.1038/nsmb982. [DOI] [PubMed] [Google Scholar]
- (18).Hockenbery D; Nuñez G; Milliman C; Schreiber RD; Korsmeyer SJ Bcl-2 Is an Inner Mitochondrial Membrane Protein That Blocks Programmed Cell Death. Nature 1990, 348 (6299), 334–336. 10.1038/348334a0. [DOI] [PubMed] [Google Scholar]
- (19).Pegoraro L; Palumbot A; Eriksont JAN; Faldat M; Giovanazzo B; Emanuel BS; Roverat G; Nowell PC; Crocet CMA 14;18 and an 8;14 Chromosome Translocation in a Cell Line Derived from an Acute B-Cell Leukemia. 1984, 81 (November), 7166–7170. 10.1073/pnas.81.22.7166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Joensuu H; Pyikkanen L; Toikkanen S Bcl-2 Protein Expression and Long-Term Survival in Breast Cancer. Am. J. Pathol. 1994, 145 (5), 1191–1198. [PMC free article] [PubMed] [Google Scholar]
- (21).McDonnell TJ; Hsieh JT; Campbell ML Expression of the Protooncogene Bcl-2 in the Prostate and Its Association with Emergence of Androgen-Independent Prostate Cancer. Cancer Res. 1992, 52 (24), 6940–6944. [PubMed] [Google Scholar]
- (22).Tjalma W; De Cuyper E; Weyler J; Van Marck E; De Pooter C; Albertyn G; Van Dam P Expression of Bcl-2 in Invasive and in Situ Carcinoma of the Uterine Cervix. Am. J. Obstet. Gynecol. 1998, 178 (1 I), 113–117. 10.1016/S0002-9378(98)70636-2. [DOI] [PubMed] [Google Scholar]
- (23).Pezzella F; Turley H; Kuzu I; Tungekar MF; Dunnill MS; Pierce CB; Harris A; Gatter KC; Mason DY Bcl-2 Protein in Non-Small-Cell Lung Carcinoma. N. Engl. J. Med. 1993, 329, 690–694. 10.1056/NEJM199309023291003. [DOI] [PubMed] [Google Scholar]
- (24).Baretton GB; Diebold J; Christoforis G; Vogt M; Müller C; Dopfer K; Schneiderbanger K; Schmidt M; Löhrs U Apoptosis and Immunohistochemical Bcl-2 Expression in Colorectal Adenomas and Carcinomas: Aspects of Carcinogenesis and Prognostic Significance. Cancer 1996, 77 (2), 255–264. . [DOI] [PubMed] [Google Scholar]
- (25).Tsujimoto Y; Croce CM Analysis of the Structure, Transcripts, and Protein Products of Bcl-2, the Gene Involved in Human Follicular Lymphoma. Proc. Natl. Acad. Sci. U. S. A. 1986, 83, 5214–5218. 10.1073/pnas.83.14.5214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Heckman C; Mochon E; Arcinas M; Boxer LM The WT1 Protein Is a Negative Regulator of the Normal Bcl-2 Allele in t(14;18) Lymphomas. J. Biol. Chem. 1997, 272 (31), 19609–19614. 10.1074/jbc.272.31.19609. [DOI] [PubMed] [Google Scholar]
- (27).Dai J; Dexheimer TS; Chen D; Carver M; Ambrus A; Roger A An Intramolecular G-Quadruplex Structure with Mixed Parallel/ Antiparallel G-Strands Formed in the Human BCL-2 Promoter Region in Solution. J Am Chem Soc. 2008, 128 (4), 1096–1098. 10.1021/ja055636a.An. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Dexheimer TS; Sun D; Hurley LH Deconvoluting the Structural and Drug-Recognition Complexity of the G-Quadruplex-Forming Region Upstream of the Bcl-2 P1 Promoter. J. Am. Chem. Soc. 2006, 128 (16), 5404–5415. 10.1021/ja0563861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Dai J; Chen D; Jones RA; Hurley LH; Yang D NMR Solution Structure of the Major G-Quadruplex Structure Formed in the Human BCL2 Promoter Region. Nucleic Acids Res. 2006, 34 (18), 5133–5144. 10.1093/nar/gkl610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Havrila M; Stadlbauer P; Islam B; Otyepka M; Šponer J Effect of Monovalent Ion Parameters on Molecular Dynamics Simulations of G-Quadruplexes. J. Chem. Theory Comput. 2017, 13 (8), 3911–3926. 10.1021/acs.jctc.7b00257. [DOI] [PubMed] [Google Scholar]
- (31).Špačková N; Berger I; Šponer J Nanosecond Molecular Dynamics Simulations of Parallel and Antiparallel Guanine Quadruplex DNA Molecules. J. Am. Chem. Soc. 1999, 121 (23), 5519–5534. 10.1021/ja984449s. [DOI] [Google Scholar]
- (32).Salsbury AM; Lemkul JA Polarizable Molecular Dynamics Simulations of C-Kit Oncogene Promoter G-Quadruplexes of Distinct Conformations. Biophys. J. 2019, 116, 360a 10.1016/j.bpj.2018.11.1959.30612714 [DOI] [Google Scholar]
- (33).Salsbury AM; Dean TJ; Lemkul JA Polarizable Molecular Dynamics Simulations of Two C-Kit Oncogene Promoter G-Quadruplexes: Effect of Primary and Secondary Structure on Loop and Ion Sampling. J. Chem. Theory Comput. 2020, 16 (5), 3430–3444. 10.1021/acs.jctc.0c00191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Gkionis K; Kruse H; Platts JA; Mládek A; Koča J; Šponer J Ion Binding to Quadruplex DNA Stems. Comparison of MM and QM Descriptions Reveals Sizable Polarization Effects Not Included in Contemporary Simulations. J. Chem. Theory Comput. 2014, 10 (3), 1326–1340. 10.1021/ct4009969. [DOI] [PubMed] [Google Scholar]
- (35).Šponer J; Bussi G; Stadlbauer P; Kührová P; Banáš P; Islam B; Haider S; Neidle S; Otyepka M Folding of Guanine Quadruplex Molecules–Funnel-like Mechanism or Kinetic Partitioning? An Overview from MD Simulation Studies. Biochim. Biophys. Acta - Gen. Subj. 2017, 1861 (5), 1246–1263. 10.1016/j.bbagen.2016.12.008. [DOI] [PubMed] [Google Scholar]
- (36).Fadrná E; Špačková N; Sarzyñska J; Koča J; Orozco M; Cheatham TE; Kulinski T; Šponer J Single Stranded Loops of Quadruplex DNA as Key Benchmark for Testing Nucleic Acids Force Fields. J. Chem. Theory Comput. 2009, 5 (9), 2514–2530. 10.1021/ct900200k. [DOI] [PubMed] [Google Scholar]
- (37).Fadrná E; Špačková N; Štefl R; Koča J; Cheatham TE; Šponer J Molecular Dynamics Simulations of Guanine Quadruplex Loops: Advances and Force Field Limitations. Biophys. J. 2004, 87 (1), 227–242. 10.1529/biophysj.103.034751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Song J; Ji C; Zhang JZH The Critical Effect of Polarization on the Dynamical Structure of Guanine Quadruplex DNA. Phys. Chem. Chem. Phys. 2013, 15 (11), 3846–3854. 10.1039/c2cp44100d. [DOI] [PubMed] [Google Scholar]
- (39).Gkionis K; Kruse H; Platts JA; Mládek A; Koča J; Šponer J Ion Binding to Quadruplex DNA Stems. Comparison of MM and QM Descriptions Reveals Sizable Polarization Effects Not Included in Contemporary Simulations. J. Chem. Theory Comput. 2014. 10.1021/ct4009969. [DOI] [PubMed] [Google Scholar]
- (40).Zhang C; Lu C; Jing Z; Wu C; Piquemal JP; Ponder JW; Ren P AMOEBA Polarizable Atomic Multipole Force Field for Nucleic Acids. J. Chem. Theory Comput. 2018, 14 (4), 2084–2108. 10.1021/acs.jctc.7b01169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Lemkul JA; MacKerell AD Polarizable Force Field for DNA Based on the Classical Drude Oscillator: II. Microsecond Molecular Dynamics Simulations of Duplex DNA. J. Chem. Theory Comput. 2017, 13 (5), 2072–2085. 10.1021/acs.jctc.7b00068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Lemkul JA; MacKerell AD Polarizable Force Field for RNA Based on the Classical Drude Oscillator. J. Comput. Chem. 2018, 39 (32), 2624–2646. 10.1002/jcc.25709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Lemkul JA; Huang J; Roux B; Mackerell AD An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev. 2016, 116, 4983–5013. 10.1021/acs.chemrev.5b00505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Lemkul JA; MacKerell AD Polarizable Force Field for DNA Based on the Classical Drude Oscillator: I. Refinement Using Quantum Mechanical Base Stacking and Conformational Energetics. J. Chem. Theory Comput. 2017, 13 (5), 2053–2071. 10.1021/acs.jctc.7b00067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Lemkul JA; Savelyev A; MacKerell AD Induced Polarization Influences the Fundamental Forces in DNA Base Flipping. J. Phys. Chem. Lett. 2014, 5 (12), 2077–2083. 10.1021/jz5009517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Savelyev A; Mackerell AD Competition among Li+, Na+, K+, and Rb+ Monovalent Ions for DNA in Molecular Dynamics Simulations Using the Additive CHARMM36 and Drude Polarizable Force Fields. J. Phys. Chem. B 2015, 119 (12), 4428–4440. 10.1021/acs.jpcb.5b00683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Salsbury AM; Lemkul JA Molecular Dynamics Simulations of the C-Kit1 Promoter G-Quadruplex: Importance of Electronic Polarization on Stability and Cooperative Ion Binding. J. Phys. Chem. B 2019, 123, 148–159. 10.1021/acs.jpcb.8b11026. [DOI] [PubMed] [Google Scholar]
- (48).Lemkul JA Same Fold, Different Properties: Polarizable Molecular Dynamics Simulations of Telomeric and TERRA G-Quadruplexes. Nucleic Acids Res. 2020, 48, 561–575. 10.1093/nar/gkz1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Dexheimer TS; Sun D; Hurley LH Deconvoluting the Structural and Drug-Recognition Complexity of the G-Quadruplex-Forming Region Upstream of the Bcl-2 P1 Promoter. J. Am. Chem. Soc. 2006, 128 (16), 5404–5415. 10.1021/ja0563861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Huppert JL; Balasubramanian S Prevalence of Quadruplexes in the Human Genome. Nucleic Acids Res. 2005, 33 (9), 2908–2916. 10.1093/nar/gki609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Costa G; Rocca R; Moraca F; Talarico C; Romeo I; Ortuso F; Alcaro S; Artese A A Comparative Docking Strategy to Identify Polyphenolic Derivatives as Promising Antineoplastic Binders of G-Quadruplex DNA c-Myc and Bcl-2 Sequences. BMC Bioinformatics 2016, 23 (4), 227–242. 10.1371/journal.pcbi.1003562. [DOI] [PubMed] [Google Scholar]
- (52).Sheu SY; Huang CH; Zhou JK; Yang DY Relative Stability of G-Quadruplex Structures: Interactions between the Human Bcl2 Promoter Region and Derivatives of Carbazole and Diphenylamine. Biopolymers 2014, 101 (10), 1038–1050. 10.1002/bip.22497. [DOI] [PubMed] [Google Scholar]
- (53).Jana J; Mondal S; Bhattacharjee P; Sengupta P; Roychowdhury T; Saha P; Kundu P; Chatterjee S Chelerythrine down Regulates Expression of VEGFA, BCL2 and KRAS by Arresting G-Quadruplex Structures at Their Promoter Regions. Sci. Rep. 2017, 329 (January), 690–694. 10.1038/srep40706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Fogolari F; Haridas H; Corazza A; Viglino P; Corà D; Caselle M; Esposito G; Xodo LE Molecular Models for Intrastrand DNA G-Quadruplexes. BMC Struct. Biol. 2009, 9, 64 10.1186/1472-6807-9-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Stadlbauer P; Kührová P; Banáš P; Koča J; Bussi G; Trantírek L; Otyepka M; Šponer J Hairpins Participating in Folding of Human Telomeric Sequence Quadruplexes Studied by Standard and T-REMD Simulations. Nucleic Acids Res. 2015, 43 (20), 9626–9644. 10.1093/nar/gkv994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).MacKerell AD; Banavali NK All-Atom Empirical Force Field for Nucleic Acids: II. Application to Molecular Dynamics Simulations of DNA and RNA in Solution. J. Comput. Chem. 2000, 21 (2), 105–120. . [DOI] [Google Scholar]
- (57).Foloppe N; MacKerell AD All-Atom Empirical Force Field for Nucleic Acids: I. Parameter Optimization Based on Small Molecule and Condensed Phase Macromolecular Target Data. J. Comput. Chem. 2000, 21 (2), 86–104. . [DOI] [Google Scholar]
- (58).Hart K; Foloppe N; Baker CM; Denning EJ; Nilsson L; MacKerell AD Optimization of the CHARMM Additive Force Field for DNA: Improved Treatment of the BI/BII Conformational Equilibrium. J. Chem. Theory Comput. 2012, 8 (1), 348–362. 10.1021/ct200723y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Brooks BR; Brooks C. Mackerell AD; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; D.M Y; Karplus M. CHARMM: Molecular Dynamics Simulation Package. J. Comput. Chem. 2009, 30 (10), 1545–1614. 10.1002/jcc.21287.CHARMM. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79 (2), 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- (61).Durell SR; Brooks BR; Ben-Naim A Solvent-Induced Forces between Two Hydrophilic Groups. J. Phys. Chem. 1994, 98 (8), 2198–2202. 10.1021/j100059a038. [DOI] [Google Scholar]
- (62).Neria E; Fischer S; Karplus M Simulation of Activation Free Energies in Molecular Systems. J. Chem. Phys. 1996, 105 (5), 1902–1921. 10.1063/1.472061. [DOI] [Google Scholar]
- (63).Beglov D; Roux B Finite Representation of an Infinite Bulk System: Solvent Boundary Potential for Computer Simulations. J. Chem. Phys. 1994, 100, 9050–9063. 10.1063/1.466711. [DOI] [Google Scholar]
- (64).Harvey Lodish, Arnold Berk, Lawrence Zipursky S, Paul Matsudaria, David Baltimore, D. J Molecular Cell Biology, 4th ed.; W.H., Freeman: New York, USA, 2000. [Google Scholar]
- (65).Phillips JC; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel RD; Kalé L; Schulten K Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26 (16), 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Feller SE; Zhang Y; Pastor RW; Brooks BR Constant Pressure Molecular Dynamics Simulation: The Langevin Piston Method. J. Chem. Phys. 1995, 103 (11), 4613–4621. 10.1063/1.470648. [DOI] [Google Scholar]
- (67).Darden T; York D; Pedersen L Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98 (12), 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- (68).Essmann U; Perera L; Berkowitz ML; Darden T; Lee H; Pedersen LG A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103 (19), 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- (69).Ryckaert JP; Ciccotti G; Berendsen HJC Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys. 1977, 23 (3), 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- (70).Miyamoto S; Kollman PA Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13 (8), 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
- (71).Lamoureux G; Harder E; Vorobyov IV; Roux B; MacKerell AD A Polarizable Model of Water for Molecular Dynamics Simulations of Biomolecules. Chem. Phys. Lett. 2006, 418 (1–3), 245–249. 10.1016/j.cplett.2005.10.135. [DOI] [Google Scholar]
- (72).Yu H; Whitfield TW; Harder E; Lamoureux G; Vorobyov I; Anisimov VM; MacKerell AD; Roux B Simulating Monovalent and Divalent Ions in Aqueous Solution Using a Drude Polarizable Force Field. J. Chem. Theory Comput. 2010, 6 (3), 774–786. 10.1021/ct900576a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Savelyev A; Mackerell AD Balancing the Interactions of Ions, Water, and DNA in the Drude Polarizable Force Field. J. Phys. Chem. B 2014, 118 (24), 6742–6757. 10.1021/jp503469s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Lamoureux G; Roux B Modeling Induced Polarization with Classical Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm. J. Chem. Phys. 2003, 119 (6), 3025–3039. 10.1063/1.1589749. [DOI] [Google Scholar]
- (75).Jiang W; Hardy DJ; Phillips JC; MacKerell AD; Schulten K; Roux B High-Performance Scalable Molecular Dynamics Simulations of a Polarizable Force Field Based on Classical Drude Oscillators in NAMD. J. Phys. Chem. Lett. 2011, 2 (2), 87–92. 10.1021/jz101461d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Lamoureux G; Roux B Modeling Induced Polarization with Classical Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm. J. Chem. Phys. 2003, 119 (6), 3025–3039. 10.1063/1.1589749. [DOI] [Google Scholar]
- (77).Chowdhary J; Harder E; Lopes PEM; Huang L; MacKerell AD; Roux B A Polarizable Force Field of Dipalmitoylphosphatidylcholine Based on the Classical Drude Model for Molecular Dynamics Simulations of Lipids. J. Phys. Chem. B 2013, 117 (31), 9142–9160. 10.1021/jp402860e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Eastman P; Swails J; Chodera JD; McGibbon RT; Zhao Y; Beauchamp KA; Wang LP; Simmonett AC; Harrigan MP; Stern CD; Wiewiora RP; Brooks BR; Pande VS OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics. PLoS Comput. Biol. 2017, 13 (7), 1–17. 10.1371/journal.pcbi.1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Huang J; Lemkul JA; Eastman PK; MacKerell AD Molecular Dynamics Simulations Using the Drude Polarizable Force Field on GPUs with OpenMM: Implementation, Validation, and Benchmarks. J. Comput. Chem. 2018, 39 (21), 1682–1689. 10.1002/jcc.25339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Andersen HC Molecular Dynamics Simulations at Constant Pressure and/or Temperature. J. Chem. Phys. 1980, 72 (4), 2384–2393. 10.1063/1.439486. [DOI] [Google Scholar]
- (81).Carpenter GA; Grossberg S ART 2: Self-Organization of Stable Category Recognition Codes for Analog Input Patterns. Appl. Opt. 1987, 26 (23), 4919–4930. 10.1364/ao.26.004919. [DOI] [PubMed] [Google Scholar]
- (82).Karpen ME; Tobias DJ; Brooks CL Statistical Clustering Techniques for the Analysis of Long Molecular Dynamics Trajectories: Analysis of 2.2-Ns Trajectories of YPGDV. Biochemistry 1993, 32 (2), 412–420. 10.1021/bi00053a005. [DOI] [PubMed] [Google Scholar]
- (83).Pao Y-H Adaptive Pattern Recognition and Neural Networks. Adapt. Pattern Recognit. Neural Networks 1989, 1–2. [Google Scholar]
- (84).Salsbury AM; Lemkul JA Polarizable Molecular Dynamics Simulations of C-Kit Oncogene Promoter G-Quadruplexes of Distinct Conformations. Biophys. J. 2019, 116 (3), 360a 10.1016/j.bpj.2018.11.1959.30612714 [DOI] [Google Scholar]
- (85).Guédin A; Gros J; Alberti P; Mergny JL How Long Is Too Long? Effects of Loop Size on G-Quadruplex Stability. Nucleic Acids Res. 2010, 38 (21), 7858–7868. 10.1093/nar/gkq639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (86).Pérez A; Marchán I; Svozil D; Sponer J; Cheatham TE; Laughton CA; Orozco M Refinement of the AMBER Force Field for Nucleic Acids: Improving the Description of α/γ Conformers. Biophys. J. 2007, 92 (11), 3817–3829. 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (87).Čech P; Kukal J; Černý J; Schneider B; Svozil D Automatic Workflow for the Classification of Local DNA Conformations. BMC Bioinformatics 2013, 14 (1), 30–32. 10.1186/1471-2105-14-205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (88).Islam B; Stadlbauer P; Krepl M; Havrila M; Haider S; Sponer J Structural Dynamics of Lateral and Diagonal Loops of Human Telomeric G-Quadruplexes in Extended MD Simulations. J. Chem. Theory Comput. 2018. 10.1021/acs.jctc.8b00543. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.