Abstract
We present here a greatly updated version of an earlier study on the conformational energies of protein−ligand complexes in the Protein Data Bank (PDB) [Nicklaus et al. Bioorg. Med. Chem. 1995, 3, 411−428], with the goal of improving on all possible aspects such as number and selection of ligand instances, energy calculations performed, and additional analyses conducted. Starting from about 357,000 ligand instances deposited in the 2008 version of the Ligand Expo database of the experimental 3D coordinates of all small-molecule instances in the PDB, we created a “high-quality” subset of ligand instances by various filtering steps including application of crystallographic quality criteria and structural unambiguousness. Submission of 640 Gaussian 03 jobs yielded a set of about 415 successfully concluded runs. We used a stepwise optimization of internal degrees of freedom at the DFT level of theory with the B3LYP/6–31G(d) basis set and a single-point energy calculation at B3LYP/6–311++G(3df,2p) after each round of (partial) optimization to separate energy changes due to bond length stretches vs bond angle changes vs torsion changes. Even for the most “conservative” choice of all the possible conformational energies— the energy difference between the conformation in which all internal degrees of freedom except torsions have been optimized and the fully optimized conformer—significant energy values were found. The range of 0 to ∼25 kcal/mol was populated quite evenly and independently of the crystallographic resolution. A smaller number of “outliers” of yet higher energies were seen only at resolutions above 1.3 Å. The energies showed some correlation with molecular size and flexibility but not with crystallographic quality metrics such as the Cruickshank diffraction-component precision index (DPI) and Rfree-R, or with the ligand instance-specific metrics such as occupancy-weighted B-factor (OWAB), real-space R factor (RSR), and real-space correlation coefficient (RSCC). We repeated these calculations with the solvent model IEFPCM, which yielded energy differences that were generally somewhat lower than the corresponding vacuum results but did not produce a qualitatively different picture. Torsional sampling around the crystal conformation at the molecular mechanics level using the MMFF94s force field typically led to an increase in energy.
Graphcial Abstract
INTRODUCTION
The noncovalent binding of a small molecule to a biological macromolecule is one of the fundamental processes in biochemistry. It is also the mechanism by which the majority of the currently approved drugs function. Most typically, an inhibitor reversibly binds to a protein to affect a biological pathway that is thought, or known, to be involved in the disease to be treated.
The efficiency of this interaction is governed by the energetics of this process. Without going into the much-discussed (but quantitatively less well-understood) details of the protein−ligand binding process, suffice it to remind the reader that the binding affinity Ka, or its reciprocal, the dissociation constant Kd, are exponentially related to the Gibbs free energy of binding ΔG via K = exp{−ΔG/RT}. ΔG has been variously decomposed into components such as ΔGinteract, ΔGsolv, ΔGmotion, and ΔGconform, denoting the contributions from the various types of protein−ligand interactions, (de)solvation effects, loss of motion of the interacting partners, and their conformational changes, respectively. It is therefore clear that conformational energy changes − including those of the small-molecule ligand − do in principle affect the binding affinity in an exponential manner.
In all current paradigms of computing molecular energies, be it molecular mechanics, semiempirical, or quantum chemical methods, calculating conformational energy differences between two sets of coordinates of the same molecule is a straightforward procedure. Such energies, taken as is, are part of the enthalpic component ΔH of the binding free energy as defined by the relationship (at constant temperature), ΔG = ΔH − TΔS. Determination of the entropic contributions of conformational changes involves evaluation of the energy hypersurface around both the reference and the bound state, a difficult procedure that is in fact rarely performed in quantitative computational approaches to determining the effects of ligand conformational changes. (Typically, a fixed heuristic value per rotatable bond is used instead, if the entropic component is considered at all.) Taking into account, however, that the absolute values of observed enthalpic and entropic contributions to ΔG are generally on the same order of magnitude, one can say that conformational energy differences (henceforth often called “conformational energies” for simplicity’s sake) are an important determinant of small-molecule binding affinities.
Therefore, if experimentally determined coordinates are available for individual cases, one should be able to determine the conformational energies involved in the binding process and, likewise, to establish distributions of such energies as they occur in nature, if sufficient examples of protein-bound ligands are available. Doing so should not only help shed light on the binding process from a fundamental biophysical perspective; perhaps more importantly, knowing the range of ligand conformational energies that occur in nature can provide important practical guides for many computational approaches in which energy thresholds can, or have to, be chosen. These approaches include docking, shape-based matching, pharmacophore searches, benchmarking of conformer generators, force-field development, and even to some extent quantum-chemical methods.
Given the fact that several hundred thousand individual ligand coordinate sets (“ligand instances”) representing about 10,000 unique small molecules are contained in the structure files of the RCSB Protein Data Bank (PDB),1 one might assume that ranges and distributions of conformational energies of small-molecule ligands have unambiguously been determined quite some time ago.
However, the question of the amount of conformational energy change seen experimentally for small-molecule ligands when binding to biomacromolecules has remained being discussed quite controversially since the first publication in this field.2 That study delivered energy values for a number of ligands extracted from X-ray crystallographically solved protein−ligand complexes in the PDB that surprised many researchers inasmuch as they populated the range between 0 and 30 kcal/mol quite evenly, with some outliers found up to about 40 kcal/mol.
A number of studies with the same or a very similar stated goal have been conducted in the intervening time. However, no clear consensus has emerged as to which energy ranges nature has realized in known protein−ligand complexes. Whereas some studies concluded that the maximum conformational energies were definitely below 10 kcal/mol,3–7 other studies delivered energy ranges up to about 25 kcal/mol,8,9 with one study even presenting both, i.e. a low energy range in the conclusion but high values in the data.10
Our 1995 study2 had unavoidable limitations, mainly stemming from the much lower available computer power at that time and the much smaller size of the crystallographic databases. As a consequence, we had to use molecular mechanics force field calculations to determine the conformational energies, had to limit ourselves to a few tens of ligand instances, and were not able to apply any filtering of the included ligand instances by crystallographic quality criteria. The present study aims at removing all these limitations to the extent currently possible. In addition, we wanted to include a series of additional quantitative analyses to shed light on the question of the provenance of the conformational energies determined from the ligand instance coordinates. One such additional analysis was the computation of quantum-chemical energies using a solvent model.
Another important aspect of the present study was to attempt to perform a thorough analysis of the “quality” of not just all protein−ligand crystal structures in the PDB but all individual ligand instances with the goal of choosing, right from the start, only the best and most-suited ligand instances for our conformational energy determinations. These aspects include setting a stricter upper crystallographic resolution limit, choosing only true bioligands (i.e., not solvent molecules etc.), and avoiding complicating factors such as titratable groups with their inherent uncertainty about protonation of the ligand in the PDB complex. We will discuss these points in more detail in the course of this paper. Our selection procedure implied that we did not want to limit ourselves to some well-known ligand sets used in related studies in the past3,8,9,11 but instead decided to evaluate each and every ligand instance available in the PDB.
We also saw it as crucial to very carefully treat the different types of internal degrees of freedom of each ligand: bond lengths, bond angles, and torsions. When applying computational approaches that involve energy minimization to experimentally determined ligand coordinates, one has to be aware of the fact that bond length differences are most likely nonexperimental artifacts caused by the computational “paradigm” used (such as the equilibrium values defined in a molecular mechanics force field’s parameter set), whereas torsional changes (above a certain limit) are most likely true, experimentally observed consequences of the ligand binding. Bond angle differences occupy a position in between the two, i.e. some may be artifacts and some may be true binding effects, which typically necessitates a pragmatic decision how to treat them. These points will be further discussed later in the paper. This implies that one has to separate these three types of internal degrees of freedom in any geometry adjustment phase that may be part of a conformational energy determination.
As tempting as it may be, when analyzing ligand X-ray coordinates as deposited in the PDB, one has to be very careful in the (necessary) removal of artifactual geometric differences in order not to fall into the trap of applying a whole host of minimizations and manipulations of the ligand to get a “good” ligand conformation − “good” being a priori defined as low-energy. In this study, we wanted to determine the conformational energies as they result from the ligand instance coordinate sets in the PDB, not predefine them. Pushing the latter case to its extreme, one could ask: Why not do an MD simulation (or docking run or other computational approach) to determine the binding conformation, i.e. why bother with an experimental cocrystal structure at all?
Once one has energies in hand determined as rigorously as possible from the experimental ligand crystal coordinates, only then can one ask the question: How much of this is an artifact, i.e. not the true binding-related conformational energy change? And if there is an artifact component to this energy, by which step(s) in the entire crystallography process of generating and depositing these coordinates, from crystal growing through data collection to model refinement, may these errors have been caused?
DATA SETS AND COMPUTATIONAL METHODS
Data Sets.
One goal of this project − in contrast to our previous study2 − was to first compile a carefully selected “high-quality” (HQ ) set of PDB ligand instances to avoid weaknesses as well as complicating factors potentially affecting the quantum-chemical energy calculations. Examples for “weaknesses” in this sense could be crystallographic resolution or B-factor values exceeding certain limits; whereas a “complicating factor” would be, e.g., the presence of a titratable group in the ligand leading to an uncertainty in the presence and location of protons (which need to be fully specified in the quantum-chemical input files).
To this goal, we initially downloaded the entire May 2008 set of ligand instances from Ligand Expo to obtain each ligand extracted from the full PDB files in the conformation bound to the macromolecule.12,13 Ligand Expo is a “sister database” of the PDB, providing the experimentally obtained 3D atom coordinates of all small molecule instances found in the PDB in a convenient “one-stop shop” way. This delivered an initial set of approximately 357,000 structures (chemical component coordinate data files).
In order to conduct the various planned analyses and filtering procedures, we needed a comprehensive annotation of all ligand instances with various types of information. For the unique identification of a ligand instance, we applied the coding scheme used by Ligand Expo, which identifies each ligand instance by its PDB ID, chemical component ID (also variously known as HET ID or ligand ID, especially when referring to ligands, not to standard residues), model number, residue number, chain ID, mmCIF sequence number, mmCIF asym. ID, and disorder flag.13 We added a series of annotations to each ligand instance that included crystallographic properties such as resolution, R factor, and Rfree, as well as other data available from the original corresponding full PDB file (downloaded as pdbml file) such as temperature during data collection, protein name, EC code, organism, biomacromolecule type, etc. From the structure of a ligand instance we calculated molecular properties (e.g., number of heavy atoms, number of hydrogen bond donors and acceptors, number of titratable groups, number of rotatable bonds) and chemical structure identifiers such as InChI and InChIKey14 as well as our own NCI/CADD Structure Identifiers (FICTS, FICuS, uuuuu).15,16 For these latter calculations we used mostly the chemoinformatics toolkit CACTVS.17,18 In order to assign a bioligand classification to the ligand instances, we annotated each instance’s Chemical Component ID by whether this ligand molecule occurred in any of the external databases Binding MOAD,19,20 PDBbind,21,22 or sc-PDB.23,24 A ligand had to occur in at least one of them to count as a true bioligand. It is noteworthy to point out that the selection of PDB ligand entries in each of these databases is based, according to their creators, on a manual analysis of this property, which thus applies by proxy to our selection of true bioligands, too. The full list of ligand annotations together with their respective sources can be found in the Spreadsheet S1 available in the Supporting Information.
An initial round of filtering of the 2008 Ligand Expo set yielded 1248 ligand instances which fulfilled our “HQ” criteria to be admissible for the energy calculation (see below for a more detailed discussion of the filtering procedure). To reduce redundancy while preserving structural diversity both on the protein and ligand side, we removed multiplicity in this set by admitting only one instance for each pair of HET ID and PDB ID; i.e. if several copies of the same ligand molecule in this raw HQ set were present for the same PDB ID, we chose only one of them for the Gaussian 03 (G03) calculations, typically the one with the lowest chain ID/residue number combination. This left us with a working set (the “HQ set” proper) of 640 ligand instances, for which G03 input files were generated and submitted (see below).
The subset of the HQ set for which G03 runs were successfully completed, be it for vacuum or solvent environment, is indicated in the following by appending “-R” (for “result”) to the set abbreviation. This HQ-R set contains 415 confirmed (see below) ligand instances, comprising 152 unique component IDs. Structure drawings for a few sample structures of the HQ set are shown in Figure S1 in the Supporting Information.
The overlap of our ligand instance sets, especially the subsets with G03 results, with ligand sets of some of the related studies mentioned before was very limited. Among the 1248 ligand instances of our HQ set, only four are also present among the 150 ligand instances in the Perola set.8 However, none of them yielded a successfully converged G03 run, thus there is no overlap with our HQ-R set. The overlap between the HQ set and the 33 ligand instances in the Boström study3 is at most six (no clear indication is given in that paper about which specific ligand instances were chosen), of which at most three remain in our HQ-R set (see Discussion). The overlap with the set of 197 PDB ligand structures in the recent study by Hawkins et al.11 was also very limited: Only five of their PDB IDs (1mzc, 1s63, 1xon, 1yc5, 2brc) were found in our list of ligand instances having G03 results; though, again, it is difficult to ascertain if all these cases represent a true overlap since the authors do not provide information about which specific ligand instances they used.
Filtering.
In the intervening time since the original download and preparation of the initial data set from Ligand Expo in 2008 and the G03 runs, a second round of PDB Remediation occurred. These remediated data were released in early 2009 and downloaded by us in February 2010. Our checks for possible changes that might affect structures and thus the conformational energies revealed that the 2009 remediation had led to (apparently undocumented) changes in the order of chains and atoms in some PDB files with ensuing changes in the nomenclature of ligand instances of particular PDB entries. We therefore established a linkage between the 2008 and 2009 nomenclatures by performing an atom-by-atom comparison of all ligand atoms′ experimental 3D coordinates for all ligand instances in our HQ sets. This was successful for the vast majority of our existing HQ-R set, yielding 415 confirmed ligand instances and only two instances that could not be confirmed and were therefore removed from the result set.25
At the time the original selection of ligand instances for the G03 runs was done, the per-residue crystallographic quality parameters, RSR (real-space R factor),26 RSCC (real-space correlation coefficient),27 and OWAB (occupancy-weighted average B-factor) were not generally available due to bulk download limitations imposed by EDS.28,29 However, EDS made them available to us in their entirety in July 2010.
Because of both these additionally available data and the second PDB remediation we decided to perform a second filtering experiment in order to evaluate how many ligand instances of our HQ-R set would pass after these changes.
Table 1 lists the entire set of filter criteria used in both the first and the second filtering runs. All data required for filtering were represented in a MySQL database;30 the filtering was performed on the basis of SQL statements created with the Python SQL toolkit SQLAlchemy.31,32 As stated before, the first filtering (2008) did not include the filter steps based on the crystallographic quality parameters “RSCC” and “RSR”. For the filtering of the 2009 Ligand Expo set, we introduced the filter “tautomers”. For the filters “DPI” and “R” we imposed stricter limits compared to the earlier filtering (ligand instances with no data present for these parameters were not admittted anymore).
Table 1.
Criteria Used for the Filtering of the Ligand Expo Ligand Instance Set
| filter name | criterion for inclusion of a Ligand Expo ligand instance |
|---|---|
| FICTS | ligand instance matches connectivity of ligand prototype (PCCD) structure compared by FICTS identifier |
| FICuS | ligand instance matches connectivity of ligand prototype (PCCD) structure compared by FICuS identifier |
| uuuuu | ligand instance matches connectivity of ligand prototype (PCCD) structure compared by uuuuu identifier |
| resolution | experimental resolution of corresponding PDB entry: ≤2 Å |
| X-ray | experimental diffraction method for the corresponding PDB entry: X-ray (e.g., powder diffraction excluded) |
| DPI | REFMAC DPI (diffraction-component precision index)33 value of the corresponding PDB entry: <0.45 Å |
| RSCC | RSCC (real-space correlation coefficient)27 of ligand instance: >0.9 |
| RSR | RSR (real-space R factor)26 of ligand instance: <0.15 |
| rotor count (lower limit) | number of rotors of the corresponding ligand prototype (PCCD) structure: >0 |
| rotor count (upper limit) | number of rotors of the corresponding ligand prototype (PCCD) structure: <15 |
| titratable groups | number of titratable groups34 of the corresponding ligand prototype (PCCD) structure: 0 |
| R | Rfree- R of corresponding PDB entry: <0.05 Å2 |
| bioligand | ligand instance is bioligand (as per occurrence of the ligand component ID in either sc-PDB, PDBbind, Binding MOAD, and/or BindingDB; see text) |
| OWAB value (lower limit) | OWAB (occupancy-weighted average B-factors) value of ligand instance: >5.0 Å2, or >2.0 Å2 if experimental resolution <1.2 Å |
| OWAB value (upper limit) | OWAB (occupancy-weighted average B-factors) value of ligand instance: <50 Å2 |
| mean B value | mean B value annotated to PDB entry: > 0 (if B value annotation is missing, pass ligand instance if average, standard deviation, and minimum of all ligand instance atom B values: >0) |
| covalent | no bonds to ligand instance are classified as covalent bond in the corresponding pdbml file entry |
| charged atoms | number of charged atoms of ligand prototype (PCCD) structure: 0 |
| tautomers | CACTVS generates no tautomers for the corresponding prototype ligand (PCCD) structure15,35 |
| macromolecule type | structure PDB keyword category of the pdbml file indicates a protein structure (i.e., DNA, RNA, etc. structures were excluded) |
| macromolecule | structure category of the pdbml file indicates a protein structure (i.e., DNA, RNA etc. structures were excluded) |
| disorder flag | disorder flag is not set for the experimental coordinate files (Ligand Expo) file |
| refinement program | structure refinement of the computing category of the pdbml file indicates unusual/low quality structure refinement methods used |
| close contact | ligand instance is not part of the MSD Ligenv data set36,37 |
In comparison to the 2008 Ligand Expo set, the number of ligand instances had grown from approximately 357,000 to 405,840 ligand structures in 2009. Applying the different criteria listed in Table 1 reduced this set by the fractions shown in Table 2. It is worthwhile to comment on the reduction rates we saw when we applied our strict connectivity match criteria between ligand instances and the corresponding ligand prototype obtained from the PDB Chemical Component Dictionary (PCCD).38 The structure normalization procedures we have developed, producing the FICTS, FICuS, and uuuuu parent structures associated with the identically named identifiers,15,16 allow one to compare structures on different levels of sensitivity for certain chemical features of a compound. The calculation of the FICTS identifier involves an only very basic level of structure normalization (e.g., corrects common drawing deficiencies for certain functional groups or involving missing hydrogen atoms); the normalization for the FICuS identifier additionally determines a canonical tautomer form; the calculation of the uuuuu identifier essentially only takes into account bare connectivity including bond order but disregards stereochemistry and all but the largest fragments (e.g., omits counterions). These three degrees of normalization were applied to both the PCCD prototype structure and all corresponding ligand instance structures. Table 2 shows that for either one of the three variants of our connectivity match criteria, we observed a surprisingly high attrition rate of about 70% loss of ligand instances.
Table 2.
Filter Strengths of the Different Ligand Filter Criteria (See Table 1) Applied to the 2009 Ligand Expo Ligand Instances Seta
| filter name | number of ligand instances | percentage of ligand instances | number of component IDs | percentage of component IDs | number of PDB entries | percentage of PDB entries |
|---|---|---|---|---|---|---|
| FICTS | 118228 | 29.1 | 5851 | 57.9 | 28409 | 62.2 |
| FICuS | 122178 | 30.1 | 6389 | 63.2 | 29626 | 64.9 |
| uuuuu | 131339 | 32.4 | 6640 | 65.7 | 30899 | 67.7 |
| resolution | 160587 | 39.6 | 5788 | 57.2 | 22508 | 49.3 |
| DPI | 188052 | 46.3 | 6278 | 62.1 | 24472 | 53.6 |
| RSCC | 196724 | 48.5 | 5931 | 58.7 | 29978 | 65.6 |
| RSR | 212207 | 52.3 | 6504 | 64.3 | 30551 | 66.9 |
| rotor count (lower limit) | 212448 | 52.3 | 9260 | 91.6 | 35802 | 78.4 |
| titratable groups | 215096 | 53.0 | 2390 | 23.6 | 30572 | 66.9 |
| R | 243170 | 59.9 | 6131 | 60.6 | 24804 | 54.3 |
| bioligand | 273311 | 67.3 | 5073 | 50.2 | 38355 | 84.0 |
| OWAB value (upper limit) | 274356 | 67.6 | 8818 | 87.2 | 40436 | 88.5 |
| covalent | 290491 | 71.6 | 8527 | 84.3 | 41283 | 90.4 |
| charged atoms | 335601 | 82.7 | 8267 | 81.8 | 41074 | 89.9 |
| tautomers | 340248 | 83.8 | 3719 | 36.8 | 39396 | 86.3 |
| OWAB value (lower limit) | 365778 | 90.1 | 9913 | 98.0 | 43392 | 95.0 |
| mean B value | 390200 | 96.1 | 9883 | 97.7 | 44448 | 97.3 |
| macromolecule type | 396742 | 97.8 | 9728 | 96.2 | 44453 | 97.3 |
| X-ray | 396763 | 97.8 | 9985 | 98.7 | 45087 | 98.7 |
| rotor count (upper limit) | 397314 | 97.9 | 9509 | 94.0 | 45300 | 99.2 |
| disorder flag | 398041 | 98.1 | 9761 | 96.5 | 45398 | 99.4 |
| refinement program | 398359 | 98.2 | 9994 | 98.8 | 45034 | 98.6 |
| macromolecule | 400872 | 98.8 | 10006 | 99.0 | 45186 | 98.9 |
| close contact | 405524 | 99.9 | 10089 | 99.8 | 45658 | 100.0 |
| no filter | 405840 | 100.0 | 10112 | 100.0 | 45667 | 100.0 |
Sorted by instance filtering strength. All numerical values given are the fractions of the ligand instances, component IDs, and PDB entries, respectively, that passed the specific filter.
These connectivity match criteria are followed by the newly added per-residue crystallographic quality parameters RSCC and RSR, which we had not used previously as explained above. Table 3 shows how the number of the 2009 Ligand Expo ligand instances is reduced step by step by applying these filters in the order shown, progressing from the strongest to the weakest filter. We applied only the FICuS filter from among our three structure connectivity filter criteria FICTS, FICuS, and uuuuu (which in fact all generated very similar filter results) because the FICuS criteria is the structural match we deem closest to how a chemist would define compound identity. If the filtering of the 2009 Ligand Expo set would have been performed with the set of criteria of the first filter experiment that had been used to generate the HQ subset of 1248 instances of the 2008 Ligand Expo set, a set of 1710 ligand structures would pass the filter chain (demonstrating a slight increase of the “pass” rate from 0.35% in the 2008 set to 0.42% in the 2009 set).
Table 3.
Consecutive Filtering of the 405,840 2009 Ligand Expo Ligand Instances and of the HQ-R Set, with Progression from Strongest to Weakest Filtera
| filter name | number of ligand instances | percentage of ligand instances | number of ligand instances (HQ-R set) | number of compound IDs (HQ-R set) | number of PDB entries (HQ-R set) |
|---|---|---|---|---|---|
| FICuS | 122179 | 30.1 | 415 | 152 | 396 |
| resolution | 61508 | 15.2 | 415 | 152 | 396 |
| DPI | 44929 | 11.1 | 319 | 115 | 301 |
| RSCC | 27125 | 6.7 | 203 | 87 | 191 |
| RSR | 25291 | 6.2 | 199 | 86 | 187 |
| rotor count (lower limit) | 12437 | 3.1 | 199 | 86 | 187 |
| titratable groups | 6781 | 1.7 | 199 | 86 | 187 |
| R | 5193 | 1.3 | 151 | 74 | 145 |
| bioligand | 767 | 0.2 | 151 | 74 | 145 |
| OWAB value (upper limit) | 750 | 0.2 | 151 | 74 | 145 |
| covalent | 581 | 0.1 | 145 | 71 | 139 |
| charged atoms | 549 | 0.1 | 145 | 71 | 139 |
| tautomers | 343 | 0.1 | 98 | 41 | 94 |
| mean B value | 343 | 0.1 | 98 | 41 | 94 |
| OWAB value (lower limit) | 343 | 0.1 | 98 | 41 | 94 |
| macromolecule type | 342 | 0.1 | 98 | 41 | 94 |
| X-ray | 342 | 0.1 | 98 | 41 | 94 |
| rotor count (upper limit) | 336 | 0.1 | 98 | 41 | 94 |
| disorder flag | 309 | 0.1 | 98 | 41 | 94 |
| refinement program | 309 | 0.1 | 98 | 41 | 94 |
| macromolecule | 309 | 0.1 | 98 | 41 | 94 |
| close contact | 309 | 0.1 | 98 | 41 | 94 |
See Table 1; filters “FICTS” and “uuuuu” omitted, see text. All numerical values given are the fractions of the ligand instances, component IDs, and PDB entries, respectively, that passed the specific filter.
Table 3 also shows the effects of the stricter filtering applied to our HQ-R set of 415 ligand instances. We will return to the resulting subset of 98 ligand instances in the Results section.
Quantum-Chemical Calculations.
All quantum-chemical (QC) calculations were performed with Gaussian 03 Rev. E01 (G03).39 For each ligand instance in the HQ set, a G03 input file was generated from the experimental 3D coordinate set originally downloaded in mmCIF format from Ligand Expo. For this conversion, the chemoinformatics toolkit CACTVS was used. Hydrogen atoms required for the QC calculations were added according to the default proton placement rules used by CACTVS. Because all molecules with titratable groups had been excluded, the addition of hydrogen atoms could be performed unambiguously.
In order to separate the different types of internal degrees of freedom, the optimization of the ligand X-ray was done in a stepwise fashion: We first optimized just the positions of the hydrogen atoms (since these were not part of the crystal coordinates) by placing constraints on all internal coordinates involving only heavy atoms thus fixing the latter in their crystal structure values; then let the bond lengths relax by releasing the constraints on bonds between heavy atoms; then released the bond angle constraints; and finally released the torsional constraints, yielding in effect a full optimization in this last stage. At the beginning, between each of these optimization stages, and at the end, a single-point (SP) calculation with a larger basis set was performed to produce the energy values used in the following analyses. The optimization stages were done at the Density Functional Theory (DFT) level of theory, using the B3LYP functional with the B3LYP/6–31G(d) basis set. The SP calculations were performed using the B3LYP/6–311++G(3df,2p) basis set. Each of these nine steps (Scheme 1) was performed in its own “Link1 segment” of a compound G03 job.
Scheme 1.

Gaussian 03 Computations To Generate Ligand Conformational Energies in Vacuum
The CACTVS script to generate the G03 input files as well as one example of such an input file are available in the Supporting Information (files with extension “.cac” and “.inp”, respectively).
In order to explore the influence of solvent on the results obtained in vacuum, we repeated the submission of G03 jobs for the 640 ligand instances of the HQ set with the same procedure as for the vacuum computations, except that aqueous solvent model computations (with dielectric constant 78.39) were added, employing the Polarizable Continuum Model using the Integral Equation Formalism variant (IEFPCM).40,41 (Based on the assumption that the very “local” optimizations of bond lengths and bond angles would not be much influenced by a solvent environment, IEFPCM was not used in the first three optimization stages [steps 2, 4, and 6 in Scheme 2].)
Scheme 2.

Gaussian 03 Computations To Generate Ligand Conformational Energies in IEFPCM Aqueous Solvent Model
For all successfully finished G03 runs we extracted the energy values in Hartree units from the output files and calculated the energy differences relative to stage 1 (Schemes 1 and 2) in kcal/mol units.
Calculation of Global Energy Minima.
Although both the relevance and the unambiguous identification of each ligand’s global energy minimum (in vacuum) in the context of this study is open to argument, we wanted to at least attempt to obtain such a conformer as an additional reference structure. A full conformational search for each ligand at the QC level described above was obviously out of the question due to the enormous CPU time this would take. Instead, we ran conformational searches for each ligand at the molecular mechanics level using the program MacroModel 9.542 (Schrödinger, Inc.) with the OPLS_2001 force field. We used the Monte Carlo method for the conformational searches, accepting the method’s default parameters in MacroModel 9.5. We kept up to three of the lowest local energy-minimum structures resulting from these runs (for some structures with only very limited flexibility, the MacroModel calculations had resulted in only two or even a single local energy minimum). We reoptimized the MacroModel structures with G03 at the QC level by initial preoptimization at the HF/3–21G level with subsequent full optimization and single-point energy calculation at the B3LYP/ 6–311++G(3df,2p)//B3LYP/6–31G(d) level of theory to ensure comparability with the energy calculations performed for the crystal conformations. The lowest of the maximally three energy values obtained in this way was defined as the global energy minimum (“GEM”).
As expected, this energy was lower in many cases than the energy of the fully torsion-optimized structure obtained in the last stage of the stepwise optimization of the ligand crystal structure conformation. In quite a few cases, however, these two energies were the same, showing that the full optimization of the ligand crystal structure had already reached the global energy minimum. Interestingly, in a few cases, the fully optimized ligand crystal structure was actually lower in energy than the Maestro structure after QC-optimization, showing that our procedure had in fact not produced the true global energy (as far as the QC computations are concerned).
Exploration of Energy Landscape Around Ligand Crystal Conformation.
At any crystallographic resolution, there is some uncertainty in the atomic positions in crystal structures. If expressed as Cartesian uncertainty, this can be translated into a torsional uncertainty for specific torsions in a small molecule, which in turn corresponds to a change in conformational energy. Dealing with this uncertainty by simply optimizing with, e.g., a flat-bottom potential with a width defined by the Cartesian uncertainty is, however, not a permissible procedure in our view since it ignores the highly anisotropic mobility of atoms in small organic molecules, in which only the torsions are typically the “effectors” of true conformational changes (vs vibrational modes, which involve all internal coordinates).
While the details of the mutual dependencies of these uncertainties can become quite complicated (e.g., the positional uncertainty is not just a function of the overall resolution but of each atom’s B factor), we wanted to explore the “energy landscapes” around the crystal conformation of our ligand instances at least in an approximate manner to get an impression how the atomic uncertainties typically affect the conformational energies.
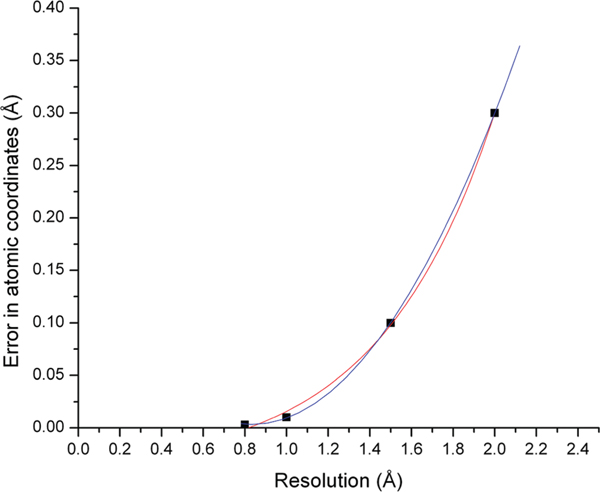
We took the values reported in ref 43 as typical atomic uncertainties at several crystallographic resolutions and used their exponential growth fit interpolation (as shown in Figure 1) in all subsequent computations.
Figure 1.
Dependency of average atomic coordinate error on crystallographic resolution. Data points taken from ref 43. Polynomial (blue) and exponential growth (red) interpolations shown (they differ very little in the resolution range of interest).
For any value of the Cartesian uncertainty, the torsional uncertainty is a function of the initial torsion value to which one applies a small change Δτ, albeit a very weak one. (Simply speaking, at a torsional value of 180°, the relative effect of a given Cartesian uncertainty is smallest because the distance between the terminal atoms of this torsion is largest and vice versa at 0°.) A strict algebraic treatment becomes very complicated as all bond length and bond angle values should enter the equation. Since the embedded bond lengths and angles for atom quartets constituting a typical rotatable bond in an organic molecule do not vary over huge ranges, we instead sampled the prototypical C−C−C−C torsion, using a bond length of 1.53 Å as employed in typical force field parameter sets. Doing this with a uniform distribution of random torsional variations yielded a torsional uncertainty of approximately 0.6 ± 0.13 degrees for a Cartesian uncertainty of 0.01 Å (see Figure S2 in the Supporting Information). The expected slight sinusoidal dependency on the initial angle with an amplitude of about 30% of the average value is clearly discernible.
Repeating this sampling procedure with a step size of 0.01 Å for the Cartesian uncertainty, we obtained that the dependency of the torsional uncertainty on the Cartesian uncertainty is essentially linear for Cartesian uncertainty values of up to 0.4 Å, with a slope of approximately 3.5° per 0.1 Å Cartesian uncertainty (Figure S3 in the Supporting Information).
We used values following from this dependency, modulated by the slight dependency on the initial torsion value mentioned above (Table S1 in the Supporting Information), to determine the width Δτ of the torsional sampling range with which we sampled the torsions of a ligand instance. Each torsion in a given ligand instance was sampled within the same interval [−Δτ,+Δτ] around its torsion value in the crystal conformation.
This sampling, to be statistically valid, involves a very large number of geometric manipulations of each ligand instance’s initial crystal coordinates with subsequent energy calculations, which cannot be done in any reasonable time frame at the QC level. Instead, we performed the energy calculations at the molecular mechanics (MM) force field level using the MMFF94s force field available in Maestro. To avoid artificial conformational energy contributions from incompatibilities of existing bond length and bond angle values with the corresponding equilibrium values in the force field’s parameter set, all bond lengths and bond angles were allowed to relax both before and after modification of the torsions. For each tested conformation, each rotatable bond in the ligand molecule was changed by a separate random value within the interval [−Δτ,+Δτ] as specified by the relationship given above. Both Gaussian and uniform distributions of these changes were tested, Δτ specifying the standard deviation in the former case and the half width of the distribution in the latter. For the subsequently generated histograms (see below), the obtained energy values of each ligand instance were binned, separately for each distribution type, into one hundred bins of equal width covering the entire energy range observed for this ligand instance. The results for Gaussian and uniform distributions of the torsional sampling were qualitatively the same. We therefore show and discuss only the results for the Gaussian distribution in the following.
From the point of view of complete coverage of the conformational space defined by the interval [−Δτ,+Δτ] around the torsion values in the crystal structure, this is a combinatorial problem. If one would like to sample each torsion, say, 100 times in this range, then a ligand with n torsions would ideally have to be sampled 100n times. Even at the MM level, this is completely prohibitive CPU time-wise for our ligand set. We instead set an upper limit of 10,000 iterations for the entire sampling for each ligand instance. Due to software performance and license limitations, even this limit was not reached in all of the runs. Visual inspection of the resulting energy difference distributions showed that a minimum of 300 iterations was needed to obtain a distribution with a reasonably smooth envelope. Application of this cutoff yielded a subset of 214 ligand instances whose energy differences to the initial crystal conformation are therefore used in the subsequent plots and discussions of ligands′ energy uncertainties as a function of crystallographic resolution.
Plots and Regressions.
All plots, unless otherwise noted, were generated with Origin 8.1 (OriginLab Corp., Northampton, MA). This software was also used for calculating the linear fits and other regressions reported. All r2 values reported in the following are “adjusted r2” values as calculated by Origin, defined as 1 − (1 − r2) [(n − 1)/(n − p − 1)], with r2 being the (conventional) coefficient of determination, n the sample size, and p the total number of regressors (without counting the constant term). Note that these values can become (slightly) negative.
To account for the nontotal rigidity of larger nonaromatic rings, in particular macrocycles, we used for some of the correlations presented an “effective rotor” count, defined as follows: nrot_eff = regular CACTVS rotor count +0.2 * (number of all single nonaromatic/nonconjugated bonds in rings of ring size >4).
RESULTS
All results of the computations described above plus various annotations such as identifier-type information, molecular properties, and crystallographic parameters for all ligand instances for which any G03 run had converged were collected in a database as described before. Those parts of the database’s contents that are of possible interest to the reader are made available as Spreadsheet S1 in the Supporting Information. Many possible correlations of, e.g., the various conformational energies with molecular properties or crystallographic quality parameters can be plotted and analyzed from this rather large data set. We will present and discuss a selection of such correlations; the ones we deem most important for the questions we set out to answer. Spreadsheet S1 allows the reader to conduct additional analyses of the data that may be of particular interest to him or her.
Vacuum Energies.
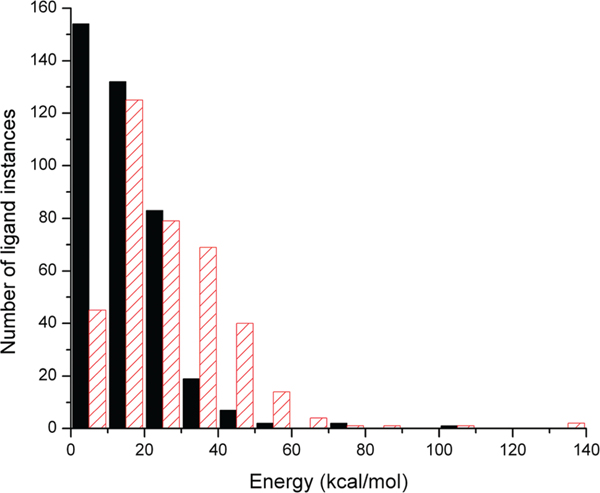
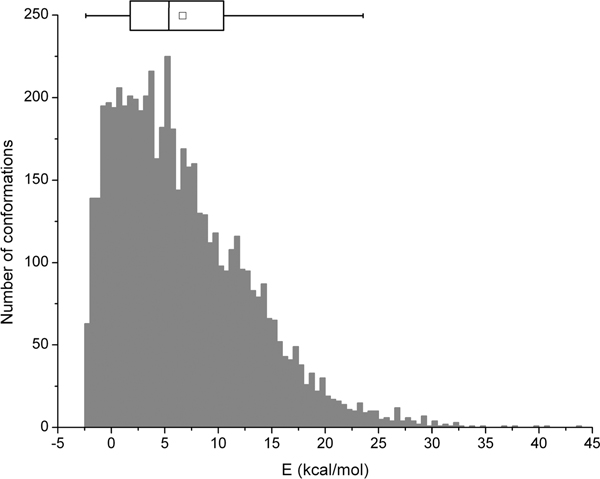
We first compare two of the vacuum conformational energy differences calculable from the set of energy values: the energy difference ΔEang‑tor between the bond angle-optimized and the fully torsion-optimized conformation and the energy difference ΔEang‑GEM between the angle-optimized conformation and the conformation found at the global energy minimum (“GEM”). From the submitted 640 runs, we obtained 400 useable results for ΔEang‑tor and 381 for ΔEang‑GEM, the remainder being mostly instances for which the G03 runs did not converge. Figure 2 shows the distribution for both the ΔEang‑tor and ΔEang‑GEM values. In both cases, one observes a significant number of instances with energy differences of up to, and even above, 40 kcal/mol. In fact, the distribution for ΔEang‑GEM reaches its maximum only in the second bin, from 10 to 20 kcal/mol. Due to the already discussed questionable validity of a vacuum global energy minimum as a reference structure we make the most “conservative” choice and will from here on plot and discuss only the values of ΔEang‑tor (unless otherwise noted). Likewise, if not further qualified, the term “conformational energies” will henceforth denote only the ΔEang‑tor values. It should thus be kept in mind that most other energy difference choices such as ΔEang‑GEM or the difference between the bond length-optimized and the fully torsion-optimized conformations would lead to yet higher conformational energies in all the subsequent plots and discussions.
Figure 2.
Histogram of conformational energy differences calculated in vacuum. Black solid bars: energy differences between bond angle-optimized and fully torsion-optimized conformations (ΔEang‑tor). Red patterned bars: energy differences between angle-optimized and global minimum energy conformations (ΔEang‑GEM).
To help interpret the conformational energies found and set the stage for the subsequent discussion, we calculated the correlation of the energies with several properties of the crystal structure or the ligand molecule itself.
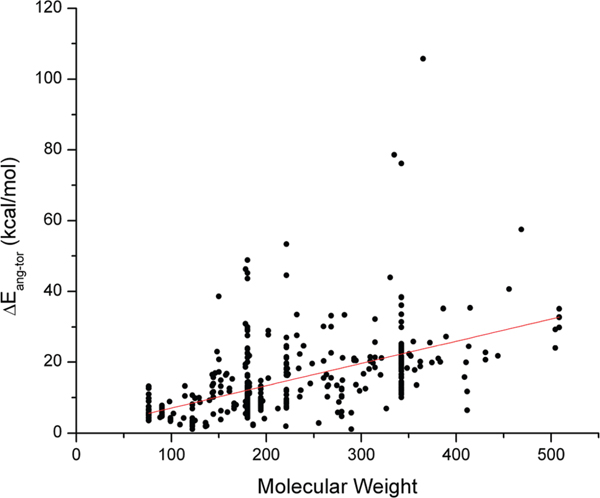
The vacuum conformational energies show a clearly discernible, though weak, correlation with the molecular weight of the ligand (r2 = 0.28), with a slope of approximately 6 kcal/mol per 100 Da (Figure 3).
Figure 3.
Vacuum conformational energies as a function of ligand molecular weight. Linear fit: Pearson’s r = 0.532, r2 = 0.281, intercept = 0.728 kcal/mol, slope = 0.063 kcal/(mol · dalton).
Likewise, we found correlations of similar strengths with both the number of heavy atoms nheavy_atoms (Pearson’s r = 0.522, r2 = 0.270, intercept = 1.505 kcal/mol, slope = 0.882 kcal/(mol · nheavy_atoms)) and the effective rotor count nrot_eff (Pearson’s r = 0.483, r2 = 0.232, intercept = 6.929 kcal/mol, slope = 2.071 kcal/(mol · nrot_eff)), and of noticeably weaker strength with the straight (nonring single-bond) rotor count (Pearson’s r = 0.374, r2 = 0.138, intercept = 9.857 kcal/mol, slope = 1.908 kcal/(mol · nrot)), shown as Figures S4−S6, respectively, in the Supporting Information. This is not surprising since all these molecular properties are expected to be significantly correlated at least in a statistical way in any sufficiently large and diverse small-molecule database (heavier molecules are more likely to possess more heavy atoms and likewise more rotatable bonds). Interestingly, the values for the energy/rotor-count ratios for both variants of the flexibility metric (2.1 and 1.9 kcal/mol per rotor for nrot_eff and nrot, respectively) in this study are very close to the corresponding ratio of 1.8 kcal/mol per rotor which we found for the equivalent “local energies” in our previous publication,2 demonstrating the robustness of this relationship.
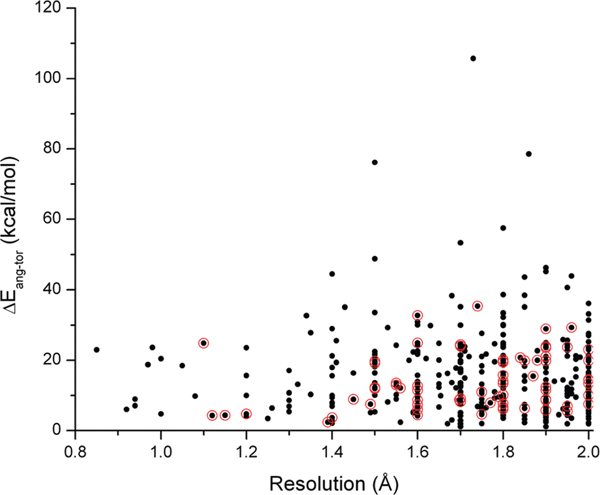
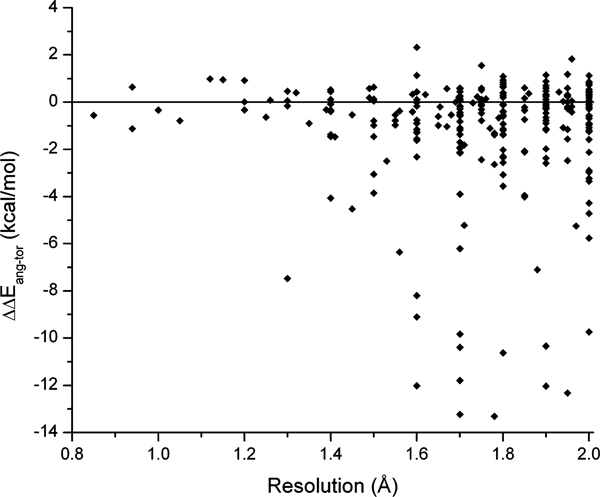
In contrast to the clearly detectable correlation of the conformational energies with molecular size type properties, no correlation was found for any of the crystallographic parameters we analyzed. Traditionally, crystallographic resolution has been used as the “quality” parameter for PDB crystal structures. When the conformational energies are plotted as a function of the resolution (Figure 4), we obtain a distribution that shows no discernible correlation given its r2 value of −0.0025. However, it is quite notable that there is a most heavily and quite uniformly populated energy range from 0 to approximately 25 kcal/mol for all resolutions in Figure 4 and that “outliers” with energies significantly above this upper bound do occur only for resolution values above approximately 1.3 Å.
Figure 4.
Vacuum conformational energies as a function of the crystallographic resolution (black dots). Linear fit: Pearson’s r = 0.0033, r2 = −0.0025. Red circles: Ultrahigh quality subset of 72 ligand instances (UHQ-R set, see text).
The use of (just) the crystallographic resolution as the global quality metric for protein (and, by extension, protein−ligand) crystal structures has come under criticism, however, for being too simplistic to truly make a statement about the quality of a crystal structure. Cruickshank therefore introduced in 1999 a diffraction-component precision index (DPI) that takes into account a number of crystallographic parameters including completeness of diffraction data, R-factor, and the resolution limit.44 The formulas for DPI were subsequently simplified by Blow for easier practical application and interpretation.33
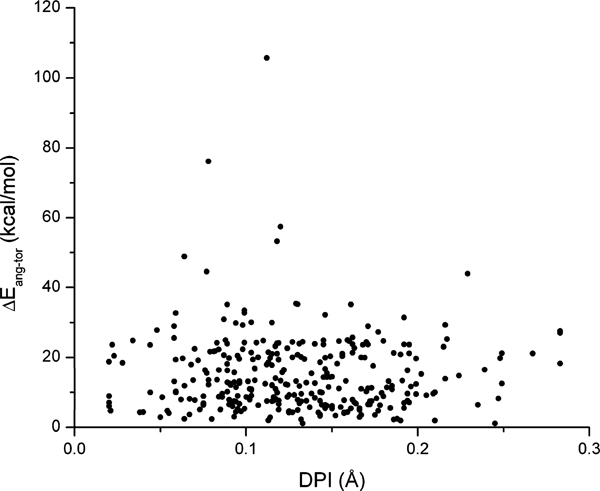
We therefore show, as an additional global metric, the distribution of the conformational energies as a function of the DPI values as available from the EDS Web site (Figure 5). Still, no correlation is present, attested by the r2 value of −0.0021.
Figure 5.
Vacuum conformational energies as a function of the Cruickshank diffraction-component precision index (DPI). Linear fit: Pearson’s r = −0.035, r2 = −0.0021. (One value at DPI > 0.3 Å not shown.)
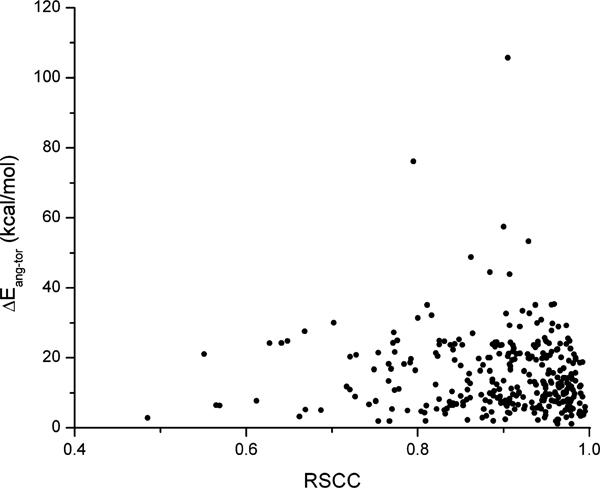
As an example of the per-residue quality criteria, or local metrics, we show the distribution of the conformational energies as a function of the real-space correlation coefficient for the ligand itself in Figure 6, which again yielded no correlation (r2 value of 0.0).
Figure 6.
Vacuum conformational energies as a function of the ligand real-space correlation coefficient (RSCC). Linear fit: Pearson’s r = −0.057, r2 = 5 × 10−5. (One value at RSCC < 0.4 not shown.)
Not shown here, but in the Supporting Information, are plots for the distributions of the conformational energies as a function of the PDB structures′ Rfree-R values (Figure S7), the ligands′ real-space R (RSR) values (Figure S8), and the ligands′ occupancy-weighted average B-factor (OWAB) values (Figure S9). We note r2 values of 0.033, −0.0031, and −0.0015, respectively, which indicates absence of correlation of the conformational energies with any of these three parameters, too.
Higher-Quality Subsets.
The per-residue crystallographic quality parameters (RSR, RSCC, OWAB), which became available to us in their entirety only in 2010, allowed us to add filtering steps to the selection filter chain mentioned above. We chose the exclusion criteria RSR > 0.2, RSCC < 0.9, OWAB > 50 Å2, and Rfree-R > 0.05 as previously used by Hawkins et al.11 Additionally, we excluded any ligand molecule that is recognized by CACTVS as being capable of prototropic tautomerism,15,35 given that the lack of resolved hydrogen atoms in PDB ligand structures introduces uncertainty about the exact tautomer that was present in the complex.45
We applied these additional filters to the HQ-R set, which led to a reduction from 415 to 98 ligand instances (Table 3), a subset we term “Very High-Quality set with Results” (VHQ-R). While all of the ligand instances with the “outlier” energy values above ∼35 kcal/mol are not present anymore in the VHQ-R set, the general picture formed by these 98 data points does not qualitatively differ from the one obtained for the larger HQ-R set of the 415 ligand instances. Likewise, correlation of the conformational energies in the VHQ-R set with the crystallographic resolution is nonexistent.
The VHQ-R set was small enough so that we could visually examine, for each ligand instance, the crystallographic coordinates deposited in the PDB inside the electron density (ED) map provided by the EDS. This was done with the help of the program Coot (Crystallographic Object-Oriented Toolkit).46,47 This visual inspection showed that even within this very high quality subset there are ligand instances for which the ligand electron density exhibits clear problems. While to some extent subjective, we therefore applied an additional round of filtering: We removed any ligand instance for which any of the following conditions applied: (a) at least one (non-hydrogen) atom was outside the electron density; (b) the difference map showed significant unmodeled ED (shown in green by Coot); (c) the difference map showed significant modeled ED inside, or very close to, the ligand ED that is not experimentally supported (shown in red by Coot); (d) the ED was very weak in general at the 1.5 σ contour level. (We also visually checked for close contacts but did not see any in this subset.) This led to further reduction of the VHQ-R set by 26 ligand instances, yielding an “Ultra High-Quality subset with Results” (UHQ-R) of 72 ligand instances. The entries of the UHQ-R set are indicated in Figure 4 by red circles around the appropriate data points. Yet again, the attrition set of 26 ligand instances could neither be clearly assigned to the high- or low-resolution domains nor to the high-or low-energy subsets. The energy values filtered out in this way ranged from 3.5 to 32.7 kcal/mol.
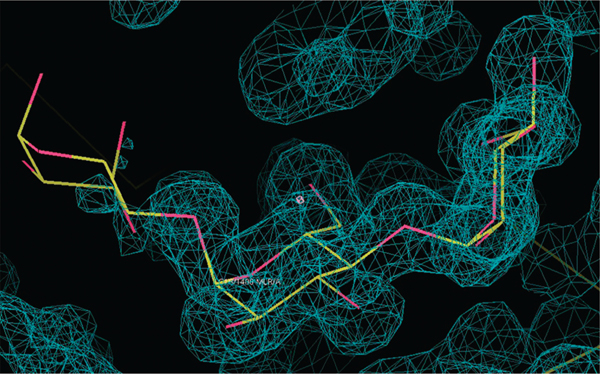
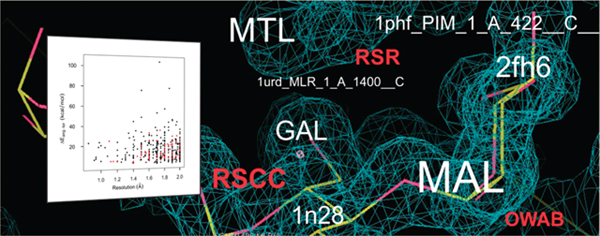
Considering all the filtering steps including by per-residue quality criteria that had been applied to create the VHQ-R set, it was quite surprising to find in over 25% of the cases significant problems with the ED that were visually immediately apparent. To give an example, ligand instance 1urd_MLR_1_A_1400__C has much weaker ED for the third ring (Figure 7) notwithstanding the fact that RSR = 0.111, RSCC = 0.973, and OWAB = 8.08 Å2, which typically would indicate a ligand structure of very high quality. This issue with the ED, taken together with its rather high energy of 29.3 kcal/mol, makes one wonder how reliable the solved conformation of this ligand instance truly is.
Figure 7.
2Fo-Fc electron density map around ligand MLR (maltotriose) in PDB entry 1urd (ligand instance 1urd_MLR_1_A_1400__C), contoured at the 0.73 e−/Å3 (1.51 σ) level. Note the mostly absent electron density around the leftmost ring at this contour level. (Figure drawn with Coot 0.6.1.46,47)
Solvent Energies.
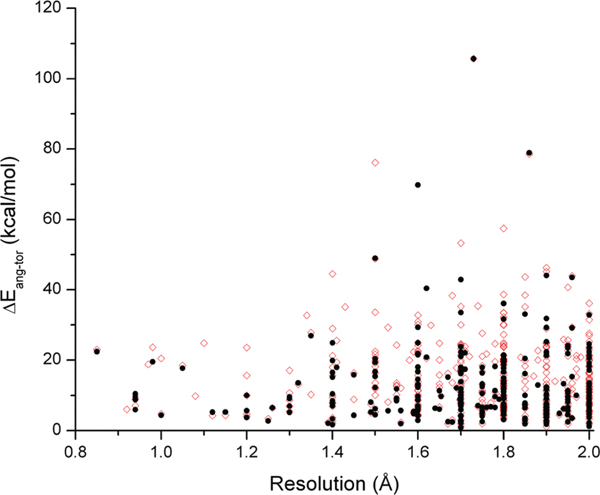
Not surprisingly, a somewhat lower percentage of the solvent model computations in G03 converged than had for the vacuum calculations. We obtained 287 usable IEFPCM solvent model results. They are plotted in Figure 8 as a function of the crystallographic resolution. As a backdrop, we also show the corresponding vacuum results (same values as shown in Figure 4).
Figure 8.
IEFPCM solvent model conformational energies as a function of the crystallographic resolution (black filled circles). Linear fit: Pearson’s r = 0.0326, r2 = −0.0025. Red open circles: vacuum conformational energies, shown for comparison.
Even though obviously many details change in comparison to the vacuum results and the graphs thins out somewhat due to the loss of more than 100 data points, the overall picture remains essentially unchanged: We again observe a predominantly populated energy range of up to about 25 kcal/mol even down to the lowest (best) resolutions, with significant outliers found only for resolution values of 1.3 Å or higher. In fact, in the majority of cases, the energies changed only very little, exemplified by an r2 value of 0.944 and a slope of 0.923 of the correlation between the solvent model and vacuum ΔEang‑tor values (Figure S10 in the Supporting Information)
In order to better understand these changes and where they may come from, Figure 9 shows the ΔΔEang‑tor values plotted as a function of the resolution.
Figure 9.
Differences of the conformational energies between vacuum and IEFPCM solvent model calculations as a function of the crystallographic resolution. Linear fit: Pearson’s r = 0.0235, adjusted r2 = −0.0032.
Just as for the conformational energies themselves (be it for vacuum or the solvent model), no correlation is present of the ΔΔEang‑tor values with the resolution. Nevertheless, similar to what is observed for the energies, below 1.3 Å the differences are confined to a narrow interval of not much more than ±1 kcal/mol. For the entire resolution range, one can discern a predominantly populated range of about ±2 kcal/mol. It is noteworthy that within this energy band, both negative and positive values occur with nearly equal frequency. In other words, use of the (calculated) solvent conformation as the reference structure can lead just as well to an increase as to a decrease of the conformational energy. Larger changes, however, with absolute values of >2 kcal/mol, were only observed in the negative direction, i.e. the solvent computations led to a decrease in ΔEang‑tor. Since this occurred, however, only for lower-resolution structures above 1.3 Å, one can again wonder if this may not rather be an indication of issues with the crystal coordinates than a genuine improvement of the reference structure that is the most appropriate for determining conformational energies.
In contrast to the situation with the conformational energies themselves, we did not find any correlation of the energy differences ΔΔEang‑tor with the two ligand size-type properties we tested, the heavy atom and the effective rotor counts (Supporting Information Figures S11 and S12, respectively).
Energy Landscape Around Ligand Crystal Conformation.
To test the widely, if not implicitly, held assumption that any energy change of a PDB ligand, when dealing with the positional uncertainties of the ligand atoms, must be “downhill,” i.e. in the direction of lower energies, we explored the energy hypersurface around the crystal conformation for a subset of ligand instances with the molecular mechanics approach described in the Methods section. Specifically, we wanted to test if the average energy change (analyzed as both the median and the arithmetic mean) is typically negative when moving away from the exact crystal ligand coordinates by randomly chosen torsional changes within a range determined by the crystallographic resolution. The results showed that this is clearly not the case.
Figure 10 depicts one example of such a histogram. For this ligand instance, coming from a crystal structure with a resolution of 2.0 Å, there were several hundred iterations that did indeed lower the energy relative to the crystal coordinates, by values of up to about 3 kcal/mol. However, many more iterations caused the energy to rise, by values of up to about 35 kcal/mol, with the consequence that the range of energy values between the lower and the upper quartile boundaries is entirely positive, with a median of 5.4 kcal/mol.
Figure 10.
Example of a histogram of the energy landscape around the crystal conformation sampled with Gaussian distribution, for ligand instance 1bk9_BU1_1__601__D_, having resolution of 2.0 Å. Energies calculated with MMFF94s. Number of iterations: 5,731. The boxplot summarizes the distribution: median: 5.4 kcal/mol; mean (□): 6.7 kcal/mol; lower quartile (Q1): 1.8 kcal/mol; upper quartile (Q3): 10.5 kcal/mol. The ends of the box-plot whiskers are drawn at the 1.5-fold distance between Q1 and Q3 subtracted/added from/to Q1 or Q3, respectively (values beyond these points can be statistically regarded as outliers).
Plotting the median values for all ligand instances for which these runs produced histograms with acceptable distributions (see Methods section) clearly shows that in most of the cases, the energy on average goes up (Figure 11). In a few cases, slightly lower median energies relative to those of the crystal conformations were observed, down to values not lower than about −4 kcal/mol. However, in the majority of cases, the median energy was above that of the crystal conformation, by values of up to nearly 50 kcal/mol in a few cases. Figure 11 also clearly reflects the approximately exponential dependency of the geometric uncertainty on the resolution we saw in Figure 1, with the concomitant resolution threshold of approximately 1.3 Å below which the median energies cluster very tightly around the initial crystal conformation energy. This shows that, while the crystal conformation may typically not be a conformational local (vacuum) energy minimum, it does not appear in most cases to be close to a local energy maximum (e.g., a structure with a bad steric clash) either.
Figure 11.
Median values of MMFF94s energies of conformations sampled around crystal conformation with random torsional changes in an interval determined by crystallographic resolution. (Gaussian distribution; 300−10,000 iterations, admitting 214 ligand instances.)
Additional Analyses.
We conducted a few additional, more spot-check type, tests of what may explain, or help interpret, the conformational energies we found.
One question that naturally arises when one thinks about conformational energies in the MM force field paradigm is, what are the main contributions to some of the high conformational energies found? I.e., do we mostly see high electrostatic or steric terms, is it predominantly torsional energy, or are there some unexpectedly high bond angle bend contributions perhaps due to steric hindrance? Since the quantum-chemical paradigm does not directly provide a decomposition of the energy into such terms, we resorted to recreating both the angle-optimized and the fully torsion-optimized conformations in a molecular modeling program (MacroModel, Schrödinger, Inc.) as closely as possible and then analyzing the individual force field terms as a surrogate for a decomposition of ΔEang‑tor. We did this not for the entire set of ligand instances (it is a somewhat tedious manual procedure) but analyzed a subset of 14 structures (eight low-energy and six high-energy ligand instances) at the borders of the populated parts of the resolution-ΔEang‑tor plane (see Figure 4). We did not find, in this admittedly somewhat anecdotal test, a common theme of the contributions to high conformational energies; i.e., different terms predominated in different cases.
Due to the mentioned exclusion of any molecule with a titratable group, we were naturally left with a comparatively large number of sugars in our ligand instance set. The question therefore came up whether carbohydrates may be particularly badly parametrized in the crystallographic refinement programs, causing them to be the main “culprits” especially for the highest ones of the conformational energies found. What exactly constitutes a “sugar” type small molecule is obviously a matter of definition (e.g., would a small glycopeptide still be a “sugar”?). In order not to overly complicate this analysis, we applied a quick heuristic sort by compound name into “sugars” and “non-sugars.” This produced an approximately 50:50 split of the HQ-R solvent subset into “sugars” and “non-sugars”. No predominance of the sugars in the very-high energy range (>30 kcal/mol) of the solvent conformational energies was found. The only perhaps noteworthy finding was that the very-low energy range from 0 to ∼5 kcal/mol is devoid of any sugars. Whether this indeed points to issues of the parametrization of the refinement programs for carbohydrates or simply is a consequence of the inherent flexibility and therefore conformational adaptation of sugars is unclear and was not further pursued.
A similar quick analysis was performed for structures containing at least one aromatic ring vs nonaromatic molecules. The question here had been whether aromatic structures may suffer from artificially high energies caused by subtle strains in their aromatic moieties that had not been fully released during the initial bond-length and bond-angle optimizations due to hindrance imposed by the remaining torsional constraints. Identification of aromatic ligands was done by the appropriate classification in CACTVS. No predominance of aromatic ligands in the high-energy domain of the solvent conformational energies was found. If anything, the aromatic ligands seemed to be somewhat more likely to populate the full energy range all the way down to 0 kcal/mol, though no separation between aromatics and nonaromatics could be based on the occupied energy range.
In an earlier stage of the project, we had taken a different selection of ligand instances directly extracted from the PDB (Ligand Expo and its predecessor, Ligand Depot, did not yet exist at that time) and subjected it to an analysis more similar to the one in our previous study.2 We took 232 small molecules that occurred as both ligands in the PDB and as pure material in the Cambridge Structural Database (CSD). For both the PDB and the CSD conformation, we calculated energies at the B3LYP/6–31+G(d) level of theory after appropriate pretreat-ment to relieve, e.g., bond length incompatibilities. Space limitations preclude us from any detailed discussion of these results.48 They are therefore made available in the Supporting Information as Spreadsheet S2. In conclusion, they do paint a picture that is entirely in agreement with the results of the current study: In the subset of 103 ligands that yielded useful results for both the PDB and CSD conformations, we obtained energies corresponding to the ΔEang‑tor values in this study of up to 25 kcal/mol and energies corresponding to ΔEang‑GEM values of up to 35 kcal/mol for the PDB ligand structures. The corresponding maximum values for the CSD conformations were somewhat lower but still significant (14 and 25 kcal/mol, respectively). After all, the structures in the CSD are not ligands in the narrow sense, though in some sense, they can be seen as ligands to themselves.
DISCUSSION
One of the central findings of our analyses is that we see no correlation of either the vacuum or solvent model energies with any but molecular size-type properties of the ligands. In particular, no correlation was found with any of the crystallographic quality parameters we investigated nor with the type of the ligand molecule.
The only threshold we saw was a resolution value around 1.3 Å, below which no “outliers” were observed. This threshold seems to be supported by statistics for the per-residue crystallographic quality criteria for high-multiplicity ligands as available at the HIC-Up Web site.49,50 A significant drop-off to better values can generally be observed there for RSR, RSCC, and OWAB at resolution values between 1.4 and 1.2 Å (see, e.g., http://xray.bmc.uu.se/hicup/FUC/fuc_eds_stats.html for fucose).
It is an interesting thought whether one should forego using any protein−ligand X-ray structure for quantitative work, especially if ligand energetics are important, solely because it has a crystallographic resolution greater than 1.3 Å. If one wants to apply an overabundance of caution, our answer at this point would be a cautious “yes”. This would come at the cost, however, of losing the vast majority of the current body of (public) macromolecular X-ray data: As of the time of this writing, applying this cutoff criteria would leave one with just 2,494 out of 76,970 PDB entries (96.8% loss) and would reduce the number of ligand hits from 12,268 to 1,002 (91.8% loss). The challenges of determining the binding mode of small heteromolecular ligands in protein−ligand complexes based on medium resolution X-ray diffraction data (including the perils of inappropriate ligand structure, force field and the absence of electrostatics during X-ray refinement) have recently been discussed by Malde and Mark.51
Omitting the outliers we observed for resolutions only above 1.3 Å, we found an energy range of up to ∼25 kcal/mol quite evenly populated by the energy differences between the angle-optimized and the fully torsion-optimized conformation (ΔEang‑tor), in both vacuum and solvent environment. It bears repeating that this energy difference constitutes the most conservative choice, i.e. any other choice that makes sense in this context leads to larger conformational energy values. At the same time, it needs to be emphasized that the high energies found constitute a range, not a necessity: Many structures, even at resolutions as high as 2.0 Å, have ΔEang‑tor values close to 0 kcal/mol.
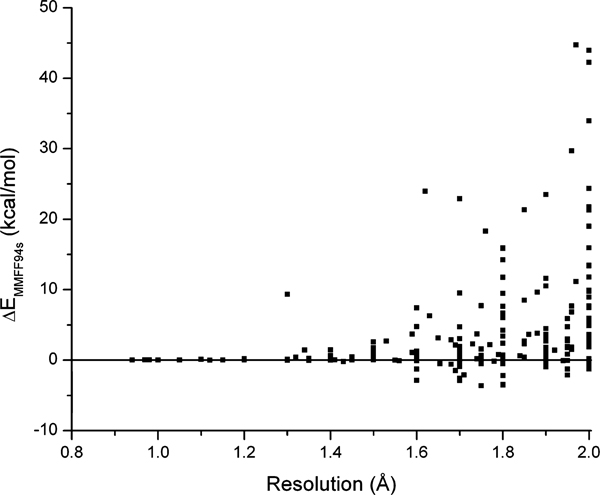
In general, both the reference structure chosen (global vs nearest local energy minimum; vacuum vs solvent model calculation) and the method used to compute the energies (quantum-chemical vs molecular mechanics; level of theory in the QC case; force field and parameter set in the MM case) have an effect on the individual energy values obtained for a specific ligand 3D coordinate set. In particular, molecular mechanics “energies” in which the electrostatic part of the potential energy function has been turned off cannot be numerically compared with our energies. However, when plotting our G03-calculated ΔEang‑GEM values vs the corresponding values computed with the general small-molecule chemistry force field MMFF94s (with electrostatics), we obtained, notwithstanding the substantial scatter for the individual values, a slope very close to unity (Figure S13 in the Supporting Information).
It appears that the general statistical conclusions are in fact quite robust vis-à-vis the specific method chosen for PDB ligand energy calculations, given that (a) the conformational energy per ligand torsional degree of freedom found in the present study was virtually the same (around 2 kcal/mol) as in our previous study2 (which used yet another MM approach, i.e. the program QUANTA with the CHARMm force field); and (b) those studies among related other work that were based on larger numbers of ligand instances (∼100 or more)8–10 all reported an upper data limit or optimal cutoff of about 25 kcal/mol.
We also note here that our solvent model calculations, while leading to noticeable changes in some of the conformational energy values vs the corresponding vacuum values, did not result in a qualitative change of the overall finding. Of course, the reaction field approach of such solvent models is not guaranteed to replicate the effect of individual water molecules forming an often quite intricate hydrogen bonding network around, and with, the ligand. Thus the issue of what is the correct reference structure for determining conformational changes of ligands when binding to an active site remains a nontrivial question, and shuttling of ligands along access channels on the protein surface has even been proposed as an alternative to binding directly from the aqueous phase. Computational methods for functional site identification suggest a substrate access channel in transaldolase.52
All energetic analyses of X-ray ligand coordinate sets have to address the issue of experimental uncertainties in the coordinates of each atom. Although statistical uncertainties in X-ray structures may result from a number of sources, ranging from data incompleteness to peculiar symmetry arrangements and others, one of the strongest variables affecting the overall accuracy of a structure is the resolution of the data set.43 These uncertainties are frequently expressed, in a first approximation and at the atomic level, by the individual B-factor (Debye−Waller factor, also known as the temperature factor) of each atom (listed in the penultimate column of the PDB file format). Most structures deposited in the PDB − with or without ligand − report isotropic B-factors only.53 Conceptually, the B-factor can be understood as the radius of an equal probability sphere for each atom within the structure considered: the larger the sphere, the higher the mobility of the atom in around its average position. Thus, the B-factors can be understood as a measure, in the quasi-harmonic approximation, of the relative thermal motion of the atoms in a structure. Note, however, that even if an anisotropic refinement was applied to the structure, the resulting B-factor matrix assigned to each atom in general represents only minor deformations of the sphere (into an ellipsoid), accounting for only the local disturbances of the atom in its microenvironment. In other words, the expression of the positional atomic uncertainties by B-factors suggests a more or less independent motion of each atom. While this may be a valid approximation for the thermal motion of atoms confined in a very rigid lattice (such as a gold single-crystal), which was the initial assumption laying the foundation of the theory in the early 1900s,54,55 this picture only partially accommodates our current understanding of the behavior of atoms in macromolecular crystals. Its literal interpretation entails a strong risk in macromolecular crystallography of proteins and their bound ligands since it could be misconstrued as suggesting that the conformational error due to atomic positional uncertainty can be simply interpreted as the displacement of the ligand atoms in an isotropic potential − and thus be relieved, in the context of ligand energy calculations, by applying Cartesian minimization of the ligand in, e.g., a flat-bottom potential. We believe such procedures are inadmissible because they ignore the very nonisotropic constraints that covalent bonds in small organic molecules impose on the displacement of ligand atoms relative to each other. The deviations observed in the mean versus atomic equilibrium positions of Gram-Charlier anharmonically refined synthetic sets help partially quantify and visualize the extent of this problem in simple cases.56
Furthermore, if the atom positions had been refined after B-factor fitting there is a possible risk of error contamination of the coordinates, which requires careful handling before a meaningful interpretation of the model is achievable.
We thus contend that, while it is generally accepted (and we have done so throughout the study) that bond lengths need to be adjusted prior to any energy determination (since differences in bond lengths are most likely due to differing equilibrium values stemming from the force field and its parameter set used in the refinement vs, e.g., the lengths resulting from a given level of theory in QC calculations), it is all too easy to erroneously minimize away the torsional changes that may be the very signature of the protein-bound conformation.
A case in point are the (only) three ligand instances in our set that were also part of the 33 ligand instances in the Boström3 set: the small-molecule inhibitor in the PDB structures 1phd, 1phe, and 1phf (Ligand Expo nomenclature for ligand instances: 1phd_PIM_1_A_422__C__,1phe_PIM_1_A_422__D__,and 1phf_PIM_1_A_422__C__). The small molecule here, though listed in the Boström paper as two different compounds, has meanwhile been chemically correctly recognized by the PDB as two tautomers of a single ligand structure, 4-phenyl-1H-imidazole (HET ID: PIM). The conformational energies reported by Boström et al. for all three ligand instances are practically zero, whereas we obtained values for ΔEang‑tor between approximately 9 and 16 kcal/mol for both vacuum and the solvent model. Chemical inspection of the molecule however immediately shows that the one single, rotatable, bond is in fact part of the conjugated system of the molecule, with the consequence that any change of that torsion by more than a few degrees will lead to a significant change in energy. It is therefore quite likely that the flat-bottomed Cartesian minimization employed by Boström et al. minimized away exactly that conformational change of the bound vs the unbound ligand that was present in the crystal.
We believe one should first analyze, in as unbiased a way as possible, what is the conformational energy that is, so to speak, in the coordinates of a ligand instance as deposited in the PDB, and only then ask the question: How much of this energy may be an artifact? There is simply no fundamental principle of nature that would dictate that any energy change due to atomic positional uncertainties of the ligand crystal structure can only be “downhill” on the energy hypersurface, i.e. in the direction of lower energies. Since it is the overall energy of the entire protein−ligand complex with all its interatomic and intermolecular interactions that has to be minimized (neglecting crystal packing forces that can further complicate the picture), one cannot apply, be it explicitly or implicitly, a variational principle to the ligand conformation by itself. In fact, the results of our procedure of sampling the entire subspace of the energy landscape around the crystal conformation by random torsional changes in a range that is a function of the crystallographic resolution strongly support this assertion: We found both lower and higher energies − with the median values in fact being typically higher, not lower.
We thus can state that even for the crystallographically highest-quality structures, we find conformational energies of up to ∼25 kcal/mol following from their 3D coordinates; and it bears repeating that other definitions of the conformational energy (difference) would yield yet higher energy ranges of perhaps up to 30 kcal/mol or more.
Thermodynamic objections are sometimes brought up against the possibility of such high ligand conformational energies. It is however important to re-emphasize that the conformational energies presented here are not ΔG values. They instead make up part of ΔH in the relatively complicated way that was discussed in the Introduction. After all, it is the overall assembly of the ligand and its binding site that has to be lower in free energy for the binding to occur, not each of the partners separately. The ligand enthalpies themselves, however, are important especially for computational approaches that (have to) use just the ligand by itself, such as pharmacophore searches.
In a similar vein, the term ”strain energies,” often used for what has been called “conformational energies” in this paper, should in our view be reserved for the phenomenon of highly strained covalently bound species such as epoxide or cyclopropane groups, which have the tendency to release this strain in an oftentimes literally explosive manner. In contrast hereto, the energy of a protein−ligand complex is an energy minimum of all the interacting partners involved irrespective whether the conformational energy of the ligand, if it were isolated, is close to, or far from, a local or the global energy minimum. In other words, the entire complex is not strained, and no explosive release of the ligand is imminent at any time.
Few experimental techniques allow one to measure directly the thermodynamic parameters ΔG, ΔH, and ΔS of interactions in solution, including of protein−ligand binding. One such technique is isothermal titration calorimetry (ITC). A collection of ITC results of receptor−ligand interactions associated with over 400 PDB structures has recently been made available to the public in an easy-to-use Web site: PDBcal (http://www.pdbcal.org).57 Sorting the entries by ΔH immediately shows that the vast majority of ΔH values fall in a range between 0 and −30 kcal/mol (indicating exothermic enthalpy change), with a handful more between −30 and −40 kcal/mol. While this is not a rigorous proof, this observation lends support to the argument that this range of energies, of up to 25 or 30 kcal/mol, is simply what is “available” in many protein−ligand binding situations through, e.g., hydrogen bond interactions, and that maximally this energy can be “spent” for ligand deformation to allow the small molecule to fit in the binding site.
From the point of view of molecular interactions this is also the energy range one can heuristically expect to be available from hydrogen bonds in a typical protein−ligand complex: Experience shows that, simply for geometric probability reasons, a protein− ligand complex rarely has more than five or six hydrogen bonds with essentially ideal geometry (each one “worth” 4−5 kcal/mol), even if the small molecule itself possesses, say, 15 or more heteroatoms.
Interestingly, in a quantum-chemical study of PDB crystal structures of 12 ligand molecules bound to multiple sites within human serum albumin,58 the authors reported enthalpic contributions of ligand reorganization for the same molecule in the different binding sites of up to 27 kcal/mol.
Still, the finding of high ligand conformational energy even in a high-quality PDB structure does not exclude the possibility that part, or even all, of this energy is an artifact, i.e. if there were a way of knowing the “true” binding conformation, one would find a lower energy. If we find such high energies even for high-resolution structures with electron densities for which refinement should proceed without any issues, then the question naturally arises: Can there be problems already at the level of the electron density itself, for which therefore no amount of refinement could recover the true bioactive bound conformation? After all, the process that yields coordinates for protein−ligand complexes deposited in the PDB is a rather complicated one. Grossly simplifying, one can identify at least the following steps: expressing the protein; growing protein crystals; synthesizing or otherwise obtaining the small-molecule ligand; soaking or cocrystallizing the ligand with the protein; transporting the cocrystal to the X-ray source, e.g. a synchrotron; mounting the crystal; exposing it to the X-ray beam, with potential radiation damage ensuing; collecting the diffracted intensities; deciding which reflections to include; and creating the initial maps, be it by direct phasing or starting from an existing model − only after which the multistep model building and refinement process to actually generate the atomic coordinates for the crystal begins.
It would by far exceed the scope of this paper to discuss all the possible sources of errors that can lead to potential issues already at the stage of the initial maps, i.e. before any atomic coordinate has been generated. We can but mention a few possibilities as they are currently being discussed in the field and otherwise point to pertinent literature.
Apart from gross errors such as mistaken identity of the ligand compound (“the wrong stuff was added”), and more subtle issues such as isomerization or other chemical change of the ligand molecule in the crystal (see, e.g., the isomerization from (+)-epi-biotin to (+)-biotin in PDB structure 2f01), one can identify the following issues that can affect the electron densities and their subsequent interpretation:
Data collection strategies
Scattering from nonspherical centers
Anharmonic vibrations during data collection
Conformational heterogeneity (mostly discussed so far in the context of the protein, not the small-molecule ligand).59–61
We will not discuss the influence of data collection strategies on electron density quality any further since they are, in many cases, instrument and sample specific and are anyway changing rapidly due to the increased degree of automation currently being introduced at the light sources.
The contribution to the diffraction pattern from nonatom centric scatterers is a far more challenging aspect of modern crystallography and one where the potential synergies between high-end modeling tools and ultrahigh resolution crystallography are the greatest. The problem, in simple terms, can be seen in the classical example of the “diamond (carbon) (2,0,0)” reflection, which can only be assigned to an off-center scatterer. The combination of modern instrumentation and better crystal growth methods have resulted, in recent years, in the availability of macromolecular electron density deformation, e.g. bond density information,62 suggesting a comparable level of detail as that observed in small molecules in the past. Although new approaches, commensurate with the complexities of real macromolecular crystals have been announced,63,64 the software used to date to process the data sets obtained for structures solved at even ultrahigh resolution remains limited to the use of atom-centric spherical scatters only.
Anharmonic contributions to the atomic displacement have been erroneously assigned as contributors to the diffuse scattering. When off-center scattering functions are included in the analysis, the inclusion of this type of correction is equally essential. Regretfully, anharmonic corrections do not offer simple, analytical solutions yet, although they can be tackled through numerical analysis or fitted through different forms of ensemble mapping.56
Similarly, the treatment of high-order multiple occupancies and micro-occupancies may not lend itself to simple analytical methods. However, the application of conformational ensembles obtained from molecular modeling techniques can be used to uncover such cases. This is particularly promising in those cases where ultrahigh resolution MAD data is available, and where the risk of overfitting the data is null.65
The equivalent of conformational heterogeneity is even observed in the area of organic small-molecule crystals, where cases are known of more than one conformer of the small molecule being present in the same crystal structure (the phenomenon there being termed conformational polymorphism). Higher-energy conformers are stabilized by stronger hydrogen bonds or more efficient close packing in the crystal structures.66 This is entirely equivalent to the situation in protein−ligand complexes, where the ensemble of ligand-protein interactions and (de)solvation forces determine the possible ligand conformations (see also Introduction). The relative contribution of each of these factors may vary in different protein−ligand structures to a different extent and therefore favor in a different manner low-energy conformations vs high-energy conformations.
A likewise very important aspect for the accurate determination of conformational energies is the question of where the protons are, i.e. of protonation and tautomerism45 of the ligand in the binding site. We circumvented this issue to a good extent in this study by simply excluding any small molecule that has any titratable group and by flagging those that are capable of tautomerism. This is obviously not a very practical strategy in protein−ligand crystallography in general. Here, too, ultrahigh resolution crystallography may provide an increasingly bountiful set of data that could help answer these questions for specific cases as well as provide more general insight by delivering solved structures that actually show individual hydrogen positions.
Finally, one should not forget that even the highest-resolution crystal structure is but one snapshot of what in reality is a highly dynamic situation of the protein−ligand interaction at physiological conditions. Thus the notion of there being one (single-valued) conformational energy may not be as straightforward as generally applied, especially in the context of assessing binding affinities.
We would argue that these and other issues, while in principle germaine to any (part of a) crystal structure in the PDB, may play themselves out more stringently for small-molecule ligands. For proteins, with their limited and well-understood range of chemistry based on 20 standard amino acids, and their strong intramolecular positional constraints (chains cannot cross through each other), scientists have learned how to obtain overall useful results even for rather poor resolutions. Also, the energy of the whole protein is not usually a value of practical interest in, e.g., drug design. In contrast hereto, these safeguards seem to often break down for the much more varied chemistry of the meanwhile more than 10,000 unique ligand molecules in the PDB.
One issue, in this context, are the well-known deficiencies for small-molecule chemistry of the libraries used in the initial model building, as well as weaknesses of the force fields used in the subsequent refinement of the models and their imple-mentation in many of the crystallographic software tools used today. The propagation of shortcomings in the available structures due to the use of improper restraints is very difficult to assess and curate appropriately. This is in part due to the evolution of the restraints used over the years and reliance on the better members of the set criteria (i.e., selection of the best structures from the PDB at any given time, most of which were refined using a previous set of restraints) to generate a newer set of restraints. This and other shortcomings may be addressable, in part, by the use of ultrahigh resolution and MAD, high resolution structures where the influence of the restraints is minimal or null.
Another approach that appears promising to address these issues is to refine (or rerefine, for existing PDB entries) a protein− ligand structure at the quantum-chemical level for at least the ligand binding site. A few successful attempts at doing so have been reported in the literature,67–74 but no incorporation of this approach into any of the standard tools in an out-of-thebox fashion is known to us at this time.
While it seems that more attention has been paid to the issue of ligand structure quality in protein−ligand complexes in the recent past,50,75–78 and a few tools have been made available to help crystallographers validate ligand structures, such as ValLigURL79,80 and a recently introduced separate section for ligands in the current version of the RCSB/PDB X-ray validation reports that includes out-of-density checks,81,82 the efforts to raise awareness of these issues appear to be still mostly limited to a few groups if not individuals.
It is also worthwhile pointing out, at this point, other efforts at, and resources for, obtaining PDB data that are curated in one way or another. One such resource is the PISCES database server83 for producing lists of sequences from the PDB using entry- and chain-specific criteria and mutual sequence identity to produce “culled” subsets of the PDB, i.e. the longest lists possible of the highest resolution structures that fulfill the given sequence identity and structural quality cut-offs.84 Such services can be used to check PDB structures for, e.g., correct protein sequences, thus for side chains in proximity of small-molecule ligands that may negatively influence the ligand structure if the incorrect amino acid was chosen.
It needs to be emphasized that whatever issues can be identified with protein−ligand structures in the PDB, it is not claimed here that this repository itself is the cause of these issues. Presumably other X-ray crystal structures would be affected in the same way. It would, however, be an intriguing question to ask whether protein−ligand structures solved in the pharmaceutical industry may statistically suffer somewhat less from these issues, given that in that context, the focus and the crystallographers′ main effort could naturally be expected to be on the small-molecule. After all, such small molecules are typically what brings in the revenue for big pharma, not the protein to which they bind. However, to our knowledge, no large-scale data sets do (publicly) exist that would allow such an analysis, although efforts are underway to make some industrial sets of crystallographic data accessible to the public.85,86
CONCLUSIONS
We have presented carefully assembled evidence that conformational energy changes of small molecules binding to proteins occur in a range of 0 to ∼25 kcal/mol even for the highest-quality crystal structures that can be currently found in the PDB, and independently of any crystallographic quality parameter we applied. A perhaps even more important conclusion is that there appear to be surprisingly few ligand data in the PDB that are reliable enough to form the basis for detailed energetic analyses. Our findings indicate that any structure above 1.3 Å crystallographic resolution has to be viewed with skepticism for this purpose; and, at any resolution, protonation and tautomerism make full knowledge of exact connectivity and conformation and thus of the totality of the binding of a ligand surprisingly difficult for many molecules. More experimental efforts seem to be needed, especially in the direction of ultrahigh resolution macromolecular crystallography, and/or higher-level refinement techniques to come to a truly unambiguous understanding of ligand conformational energies in the sense that one could routinely trust such energies calculated down to a precision of, say, one kcal/mol.
Supplementary Material
ACKNOWLEDGMENTS
This study utilized the high-performance computational capabilities of the Helix Systems at the National Institutes of Health, Bethesda, MD (http://helix.nih.gov). We thank Doug Fox for his help in putting together the protocol used in the Gaussian 03 input files for the stepwise optimization of the ligand instances. We thank Gerard DVD Kleywegt and Mark Harris for making the crystallographic quality data from the EDS server available to us. We thank Adel Golovin for making close contact data for PDB protein–ligand complexes available to us. We thank Paul Hawkins and Greg Warren for insightful discussions. We thank John Westbrook for providing us with statistical numbers about PDB entries as well as for useful discussions. This project has been funded in part with federal funds from the National Cancer Institute, National Institutes of Health, under contract HHSN261200800001E. The content of this publication does not necessarily reflect the views or policies of the Department of Health and Human Services, nor does mention of trade names, commercial products, or organizations imply endorsement by the U.S. Government.
Footnotes
ASSOCIATED CONTENT
Supporting Information
A spreadsheet for all 415 ligand instances for which at least one G03 run completed successfully, with all annotations and computational results included; the CACTVS script used to generate the G03 input files; an example of such a G03 input file; an MS Word document with sample ligand structures, a number of additional graphs as described in the text, and a table of the average torsional uncertainty of the “prototype” C−C−C-C torsion; and a spreadsheet with the results of the previous analysis of both CSD and PDB small-molecule structures as mentioned in the text. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
REFERENCES
- (1).RCSB Protein Data Bank. http://www.pdb.org/pdb/static.do?p=download/ftp/index.html (accessed Aug 19, 2011).
- (2).Nicklaus MC; Wang S; Driscoll JS; Milne GWA Conformational Changes of Small Molecules Binding to Proteins. Bioorg. Med. Chem. 1995, 3, 411–428. [DOI] [PubMed] [Google Scholar]
- (3).Boström J; Norrby P-O; Liljefors T Conformational Energy Penalties of Protein-Bound Ligands. J. Comput.-Aided Mol. Des. 1998, 12, 383–396. [DOI] [PubMed] [Google Scholar]
- (4).Demeter DA; Weintraub HJR; Knittel JJ The Local Minima Method (LMM) of Pharmacophore Determination: A Protocol for Predicting the Bioactive Conformation of Small, Conformationally Flexible Molecules. J. Chem. Inf. Model. 1998, 38, 1125–1136. [DOI] [PubMed] [Google Scholar]
- (5).Vieth M; Hirst JD; Brooks CL Do Active Site Conformations of Small Ligands Correspond to Low Free-Energy Solution Structures? J. Comput.-Aided Mol. Des. 1998, 12, 563–572. [DOI] [PubMed] [Google Scholar]
- (6).Hao M-H; Haq O; Muegge I Torsion Angle Preference and Energetics of Small-Molecule Ligands Bound to Proteins. J. Chem. Inf. Model. 2007, 47, 2242–2252. [DOI] [PubMed] [Google Scholar]
- (7).Labute P High Strain Energies of Bound Ligands: What is Going on? Abstracts of Papers, 232th National Meeting of the American Chemical Society, San Francisco, CA, September 10–14, 2006; American Chemical Society: Washington, DC, 2006; CINF 76. [Google Scholar]
- (8).Perola E; Charifson PS Conformational Analysis of Drug-Like Molecules Bound to Proteins: An Extensive Study of Ligand Reorganization upon Binding. J. Med. Chem. 2004, 47, 2499–2510. [DOI] [PubMed] [Google Scholar]
- (9).Kirchmair J; Wolber G; Laggner C; Langer T Comparative Performance Assessment of the Conformational Model Generators Omega and Catalyst: A Large-Scale Survey on the Retrieval of Protein-Bound Ligand Conformations. J. Chem. Inf. Model. 2006, 46, 1848–1861. [DOI] [PubMed] [Google Scholar]
- (10).Butler KT; Luque FJ; Barril X Toward Accurate Relative Energy Predictions of the Bioactive Conformation of Drugs. J. Comput. Chem. 2009, 30, 601–610. [DOI] [PubMed] [Google Scholar]
- (11).Hawkins PCD; Skillman AG; Warren GL; Ellingson BA; Stahl MT Conformer Generation with OMEGA: Algorithm and Validation Using High Quality Structures from the Protein Databank and Cambridge Structural Database. J. Chem. Inf. Model. 2010, 50, 572–584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Feng Z; Chen L; Maddula H; Akcan O; Oughtred R; Berman HM; Westbrook J Ligand Depot: A Data Warehouse for Ligands Bound to Macromolecules. Bioinformatics 2004, 20, 2153–2155. [DOI] [PubMed] [Google Scholar]
- (13).Ligand Expo Downloads. http://ligand-expo.rcsb.org/lddownload.html (accessed Aug 19, 2011).
- (14).InChI-Trust.org - History of InChI. http://www.inchi-trust.org/index.php?q=node/2 (accessed Aug 19, 2011).
- (15).Sitzmann M; Ihlenfeldt W-D; Nicklaus MC Tautomerism in Large Databases. J. Comput.-Aided Mol. Des. 2010, 24, 521–551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Sitzmann M; Filippov IV; Nicklaus MC Internet Resources Integrating Many Small-Molecule Databases. SAR QSAR Environ. Res. 2008, 19, 1–9. [DOI] [PubMed] [Google Scholar]
- (17).Ihlenfeldt WD; Takahashi Y; Abe H; Sasaki S Computation and Management of Chemical Properties in CACTVS: An Extensible Networked Approach toward Modularity and Compatibility. J. Chem. Inf. Comput. Sci. 1994, 34, 109–116. [Google Scholar]
- (18).Xemistry GmbH - Homepage. http://xemistry.com/ (accessed Aug 19, 2011).
- (19).Hu L; Benson ML; Smith RD; Lerner MG; Carlson HA Binding MOAD (Mother Of All Databases). Proteins 2005, 60, 333–340. [DOI] [PubMed] [Google Scholar]
- (20).BindingMoad.org - The Mother Of All Databases. http://www.bindingmoad.org/ (accessed Aug 19, 2011).
- (21).Wang R; Fang X; Lu Y; Yang C-Y; Wang S The PDBbind Database: Methodologies and Updates. J. Med. Chem. 2005, 48, 4111–4119. [DOI] [PubMed] [Google Scholar]
- (22).PDBBind Database. http://sw16.im.med.umich.edu/databases/pdbbind/index.jsp (accessed Aug 19, 2011).
- (23).Kellenberger E; Muller P; Schalon C; Bret G; Foata N; Rognan D sc-PDB: An Annotated Database of Druggable Binding Sites from the Protein Data Bank. J. Chem. Inf. Model. 2006, 46, 717–727. [DOI] [PubMed] [Google Scholar]
- (24).sc- PDB: An Annotated Database of Druggable Binding Sites from the Protein DataBank. http://cheminfo.u-strasbg.fr:8080/scPDB/2010/db_search/acceuil.jsp?uid=8007386333108703232 (accessed Aug 19, 2011). [DOI] [PubMed]
- (25).Two ligand instances in our original 2008. HQ-R set were not present any more in the same way in the newly downloaded Ligand Expo files. One, 2ao0_FID_1__360__D__, had become labeled as “obsolete” in the PDB, with now different coordinates in the indicated replacement entry 3H4G. The other, 1l2i_ETC_1__600__F___, was not found in the 2010 Ligand Expo with the updated nomenclature (though it still was there with the obsolete nomenclature). Not being able to ascertain what this may mean for the validity of these PDB entries, we decided to possibly err on the side of caution and therefore removed these two ligand occurrences from all current result lists (HQ-R sets).
- (26).Jones TA; Zou JY; Cowan SW; Kjeldgaard M Improved Methods for Building Protein Models in Electron Density Maps and the Location of Errors in these Models. Acta Crystallogr., Sect. A: Found Crystallogr. 1991, 47, 110–119. [DOI] [PubMed] [Google Scholar]
- (27).Murshudov GN; Vagin AA; Dodson EJ Refinement of Macromolecular Structures by the Maximum-Likelihood Method. Acta Crystallogr., Sect. D: Biol. Crystallogr. 1997, 53, 240–255. [DOI] [PubMed] [Google Scholar]
- (28).Kleywegt GJ; Harris MR; Zou JY; Taylor TC; Wählby A; Jones TA The Uppsala Electron-Density Server. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2004, 60, 2240–2249. [DOI] [PubMed] [Google Scholar]
- (29).EDS - Uppsala Electron Density Server. http://eds.bmc.uu.se/eds/ (accessed Sep 3, 2010).
- (30).MySQL - Homepage. http://www.mysql.com/ (accessed Sep 17, 2010).
- (31).Python Programming Language - Homepage. http://www.python.org/ (accessed Sep 17, 2010).
- (32).SQLAlchemy - The Database Toolkit for Python. http://www.sqlalchemy.org/ (accessed Dec 9, 2011).
- (33).Blow DM Rearrangement of Cruickshank’s Formulae for the Diffraction-Component Precision Index. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2002, 58, 792–797. [DOI] [PubMed] [Google Scholar]
- (34).Boolean calculation of the number of protonable and deprotonable groups as retrieved by the property G_TITRATION from a molecular ensemble available in a CACTVS standard distribution.
- (35).Oellien F; Cramer J; Beyer C; Ihlenfeldt W-D; Selzer PM The Impact of Tautomer Forms on Pharmacophore-Based Virtual Screening. J. Chem. Inf. Model. 2006, 46, 2342–2354. [DOI] [PubMed] [Google Scholar]
- (36).Golovin A; Dimitropoulos D; Oldfield T; Rachedi A; Henrick K; MSDsite A Database Search and Retrieval System for the Analysis and Viewing of Bound Ligands and Active Sites. Proteins: Struct., Funct., Bioinf 2005, 58, 190–199. [DOI] [PubMed] [Google Scholar]
- (37).Golovin A (personal communication, January 23, 2008). [Google Scholar]
- (38).Ligand Expo Downloads. http://ligand-expo.rcsb.org/ld-download.html (accessed Nov 19, 2011).
- (39).Gaussian 03 Release Notes. http://www.gaussian.com/g_misc/g03/g03_rel.htm (accessed Dec 15, 2010).
- (40).Tomasi J; Mennucci B; Cammi R Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [DOI] [PubMed] [Google Scholar]
- (41).G09 Keyword: SCRF. http://www.gaussian.com/g_tech/g_ur/k_scrf.htm (accessed Dec 8, 2011).
- (42).MacroModel; Schrodinger, LLC: New York, NY, 2011. [Google Scholar]
- (43).Cachau RE; Podjarny AD High-Resolution Crystallography and Drug Design. J. Mol. Recognit. 2005, 18, 196–202. [DOI] [PubMed] [Google Scholar]
- (44).Cruickshank DWJ Remarks About Protein Structure Precision. Acta Crystallogr., Sect. D: Biol. Crystallogr. 1999, 55, 583–601. [DOI] [PubMed] [Google Scholar]
- (45).ten Brink T; Exner TE Influence of Protonation, Tautomeric, and Stereoisomeric States on Protein−Ligand Docking Results. J. Chem. Inf. Model. 2009, 49, 1535–1546. [DOI] [PubMed] [Google Scholar]
- (46).Emsley P; Lohkamp B; Scott WG; Cowtan K Features and Development of Coot. Acta Crystallogr., Sect. D: Biol. Crystallogr 2010, 66, 486–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Coot. http://www.biop.ox.ac.uk/coot/ (accessed Dec 15, 2010).
- (48).Weidlich IE; Nicklaus MC Conformational Energy of Bioactive Ligand-Protein Complexes. Abstracts of Papers, 232th National Meeting of the American Chemical Society, San Francisco, CA, September 10–14, 2006; American Chemical Society: Washington, DC, 2006; COMP 219. [Google Scholar]
- (49).HIC-Up. http://xray.bmc.uu.se/hicup/ (accessed Mar 29, 2011).
- (50).Kleywegt GJ Crystallographic Refinement of Ligand Complexes. Acta Crystallogr., Sect. D; Biol. Crystallogr. 2007, 63, 94–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Malde AK; Mark AE Challenges in the Determination of the Binding Modes of Non-Standard Ligands in X-ray Crystal Complexes. J. Comput.-Aided Mol. Des. 2011, 25, 1–12. [DOI] [PubMed] [Google Scholar]
- (52).Silberstein M; Landon M; Wang Y; Perl A; Vajda S Computational Methods for Functional Site Identification Suggest a Substrate Access Channel in Transaldolase. Genome Inform. 2006, 17, 13–22. [PubMed] [Google Scholar]
- (53).Westbrook J 11475 entries have reported TLS refinements; 7134 entries report anisotropic temperature factor data; 3408 entries contain both TLS details and anisotropic temperature factor data (personal communication, February 2011). [Google Scholar]
- (54).Debye P Interferenz von Röntgenstrahlen und Wärmebewegung. Ann. Phys. 1913, 348, 49–92. [Google Scholar]
- (55).Waller I Zur Frage der Einwirkung der Wärmebewegung auf die Interferenz von Röntgenstrahlen. Z. Phys. A: At. Nucl. 1923, 17, 398–408. [Google Scholar]
- (56).Reilly AM; Morrison CA; Rankin DWH Using Molecular-Dynamics Simulations to Understand and Improve the Treatment of Anharmonic Vibrations. I. Study of Positional Parameters. Acta Crystallogr., Sect. A: Found Crystallogr. 2011, 67, 336–345. [DOI] [PubMed] [Google Scholar]
- (57).Li L; Dantzer JJ; Nowacki J; O′Callaghan BJ; Meroueh SO PDBcal: A Comprehensive Dataset for Receptor−Ligand Interactions with Three-dimensional Structures and Binding Thermody-namics from Isothermal Titration Calorimetry. Chem. Biol. Drug Des. 2008, 71, 529–532. [DOI] [PubMed] [Google Scholar]
- (58).Wembridge P; Robinson H; Novak I Computational Study of Ligand Binding to Protein Receptors. Bioorg. Chem. 2008, 36, 288–294. [DOI] [PubMed] [Google Scholar]
- (59).Burling FT; Weis WI; Flaherty KM; Brünger AT Direct Observation of Protein Solvation and Discrete Disorder with Experimental Crystallographic Phases. Science 1996, 271, 72–77. [DOI] [PubMed] [Google Scholar]
- (60).DePristo MA; de Bakker PIW; Blundell TL Heterogeneity and Inaccuracy in Protein Structures Solved by X-ray Crystallography. Structure 2004, 12, 831–838. [DOI] [PubMed] [Google Scholar]
- (61).Knight JL; Zhou Z; Gallicchio E; Himmel DM; Friesner RA; Arnold E; Levy RM Exploring Structural Variability in X-ray Crystallographic Models Using Protein Local Optimization by Torsion-Angle Sampling. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2008, 64, 383–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Guillot B; Jelsch C; Podjarny A; Lecomte C Charge-Density Analysis of a Protein Structure at Subatomic Resolution: The Human Aldose Reductase Case. Acta Crystallogr., Sect. D: Biol. Crystallogr 2008, 64, 567–588. [DOI] [PubMed] [Google Scholar]
- (63).Afonine PV; Lunin VY; Muzet N; Urzhumtsev A On the Possibility of the Observation of Valence Electron Density for Individual Bonds in Proteins in Conventional Difference Maps. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2004, 60, 260–274. [DOI] [PubMed] [Google Scholar]
- (64).Afonine PV; Urzhumtsev A On a Fast Calculation of Structure Factors at a Subatomic Resolution. Acta Crystallogr., Sect. A: Found Crystallogr 2004, 60, 19–32. [DOI] [PubMed] [Google Scholar]
- (65).Podjarny A; Schneider TR; Cachau RE; Joachimiak A Structural Information Content at High Resolution: MAD versus Native. In Macromolecular Crystallography, Part D; Academic Press: Waltham, MA, 2003; Vol. 374, pp 321–341. [DOI] [PubMed] [Google Scholar]
- (66).Nangia A Conformational Polymorphism in Organic Crystals. Acc. Chem. Res. 2008, 41, 595–604. [DOI] [PubMed] [Google Scholar]
- (67).Nilsson K; Ryde U Protonation Status of Metal-Bound Ligands can be Determined by Quantum Refinement. J. Inorg. Biochem. 2004, 98, 1539–1546. [DOI] [PubMed] [Google Scholar]
- (68).Ryde U Accurate Metal-Site Structures in Proteins Obtained by Combining Experimental Data and Quantum Chemistry. Dalton Trans. 2007, 607. [DOI] [PubMed] [Google Scholar]
- (69).Ryde U; Greco C; De Gioia L Quantum Refinement of [FeFe] Hydrogenase Indicates a Dithiomethylamine Ligand. J. Am. Chem. Soc. 2010, 132, 4512–4513. [DOI] [PubMed] [Google Scholar]
- (70).Fuchs MGG; Meyer F; Ryde U A Combined Computational and Experimental Investigation of the [2Fe−2S] Cluster in Biotin Synthase. J. Biol. Inorg. Chem. 2009, 15, 203–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (71).Yu N; Yennawar HP; Merz KM Jr. Refinement of Protein Crystal Structures Using Energy Restraints Derived from Linear-Scaling Quantum Mechanics. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2005, 61, 322–332. [DOI] [PubMed] [Google Scholar]
- (72).Li X; He X; Wang B; Merz K Conformational Variability of Benzamidinium-Based Inhibitors. J. Am. Chem. Soc. 2009, 131, 7742–7754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Yu N; Li X; Cui G; Hayik SA; Merz KM Critical Assessment of Quantum Mechanics Based Energy Restraints in Protein Crystal Structure Refinement. Protein Sci. 2006, 15, 2773–2784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Li X; Hayik SA; Merz KM Jr. QM/MM X-Ray Refinement of Zinc Metalloenzymes. Chem. Biol. Drug. Des. 2010, 104, 512–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (75).Davis AM; Teague SJ; Kleywegt GJ Application and Limitations of X-Ray Crystallographic Data in Structure-Based Ligand and Drug Design. Angew. Chem., Int. Ed. Engl. 2003, 42, 2718–2736. [DOI] [PubMed] [Google Scholar]
- (76).Kleywegt GJ; Henrick K; Dodson EJ; van Aalten DMF Pound-Wise but Penny-Foolish: How Well do Micromolecules Fare in Macromolecular Refinement? Structure 2003, 11, 1051–1059. [DOI] [PubMed] [Google Scholar]
- (77).Mooij WTM; Hartshorn MJ; Tickle IJ; Sharff AJ; Verdonk ML; Jhoti H Automated Protein−Ligand Crystallography for Structure-Based Drug Design. J. Med. Chem. 2006, 1, 827–838. [DOI] [PubMed] [Google Scholar]
- (78).Davis AM; St-Gallay SA; Kleywegt GJ Limitations and lessons in the use of X-ray structural information in drug design. Drug Discovery Today 2008, 13, 831–841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Kleywegt GJ; Harris MR; ValLigURL A Server for LigandStructure Comparison and Validation. Acta Crystallogr., Sect. D: Biol. Crystallogr 2007, 63, 935–938. [DOI] [PubMed] [Google Scholar]
- (80).ValLigURL - Validation of Ligands. http://eds.bmc.uu.se/eds/valligurl.php (accessed Aug 19, 2011).
- (81).Westbrook J (personal communication, August 19, 2011). [Google Scholar]
- (82).Validation Server. http://validate.rcsb.org/ (accessed Aug 20, 2011).
- (83).Home - Dunbrack Lab. http://dunbrack.fccc.edu/Home.php (accessed Aug 20, 2011).
- (84).Wang G; Dunbrack RL PISCES: Recent Improvements to a PDB Sequence Culling Server. Nucleic Acids Res. 2005, 33, W94–W98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (85).Carlson HA; Dunbar JB A Call to Arms: What You can do for Computational Drug Discovery. J. Chem. Inf. Model. 2011, 51, 2025–2026. [DOI] [PubMed] [Google Scholar]
- (86).CSARdock.org - Home. http://www.csardock.org/MainContent.jsp?page=include/csar-faq-1.jsp (accessed Nov 19, 2011).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.