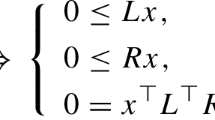Skip to main content
SpringerLink
Log in

A path following method for LCP withsuperlinearly convergent iteration sequence

  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

A new algorithm for solving linear complementarity problems with sufficient matrices isproposed. If the problem has a solution, the algorithm is superlinearly convergent from anypositive starting points, even for degenerate problems. Each iteration requires only onematrix factorization and at most two backsolves. Only one backsolve is necessary if theproblem is known to be nondegenerate. The algorithm generates points in a large neighborhoodof the central path and has the lowest iteration complexity obtained so far in theliterature. Moreover, the iteration sequence converges superlinearly to a maximal solutionwith the same Q-order as the complementarity sequence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J.F. Bonnans and C.C. Gonzaga, Convergence of interior point algorithms for the monotone linear complementarity problem, Research Report, INRIA, P.O. Box 105, 78153 Rocquencourt, France, 1993; to appear in Mathematics of Operations Research.

    Google Scholar 

  2. J.F. Bonnans and F.A. Potra, Infeasible path following algorithms for linear complementarity problems, Reports on Computational Mathematics 63, Department of Mathematics, The University of Iowa, Iowa City, IA 52242, USA, December 1994.

    Google Scholar 

  3. R.W. Cottle, J.-S. Pang and R.E. Stone, The Linear Complementarity Problem, Academic Press, Boston, MA, 1992.

    Google Scholar 

  4. W. Cottle, J.-S. Pang and V. Venkateswaran, Sufficient matrices and the linear complementarity problem, Linear Algebra and Its Applications 114y115(1989)231–249.

    Article  Google Scholar 

  5. J. Ji, F.A. Potra and S. Huang, A predictor-corrector method for linear complementarity problems with polynomial complexity and superlinear convergence, Journal of Optimization Theory and Applications 84(1995)187–199.

    Article  Google Scholar 

  6. M. Kojima, N. Megiddo, T. Noma and A. Yoshise, A Unified Approach to Interior Point Algorithms for Linear Complementarity Problems, Lecture Notes in Comput. Sci. 538, Springer, 1991.

  7. K.A. McShane, Superlinearly convergent O (√nL)-iteration interior-point algorithms for linear programming and the monotone linear complementarity problem, SIAM Journal on Optimization 4(1994)247–261.

    Article  Google Scholar 

  8. S. Mizuno, A superlinearly convergent infeasible-interior-point algorithm for geometrical LCPs without a strictly complementary condition, Mathematics of Operations Research 21(1996)382–400.

    Article  Google Scholar 

  9. F.A. Potra, On Q-order and R-order of convergence, Journal of Optimization Theory and Applications 63(1989)415–431.

    Article  Google Scholar 

  10. F. A. Potra, An O(nL) infeasible-interior-point algorithm for LCP with quadratic convergence, Reports on Computational Mathematics 50, Department of Mathematics, The University of Iowa, Iowa City, IA 52242, USA, January 1994.

    Google Scholar 

  11. F.A. Potra and R. Sheng, A large-step infeasible-interior-point method for the P*-matrix LCP, SIAM Journal on Optimization 7(1997)318–335.

    Article  Google Scholar 

  12. F.A. Potra and R. Sheng, Predictor-corrector algorithms for solving P*( κ)-matrix LCP from arbitrary positive starting points, Mathematical Programming 76(1997)223–244.

    Article  Google Scholar 

  13. F.A. Potra and R. Sheng, A superlinearly convergent infeasible-interior-point algorithm for degenerate LCP, Reports on Computational Mathematics 66, Department of Mathematics, The University of Iowa, Iowa City, IA 52242, USA, February 1995.

    Google Scholar 

  14. R.W.H. Sargent, Infeasible-interior-point method for generalized monotone linear complementarity problems, Report Series C94 12, Center for Process Systems Engineering, Imperial College, London, 1994.

    Google Scholar 

  15. H. Väliaho, P*-matrices are just sufficient, Linear Algebra and Its Applications 239(1996)103–108.

    Article  Google Scholar 

  16. S.J. Wright, A path-following infeasible-interior-point algorithm for linear complementarity problems, Optimization Methods and Software 2(1993)79–106.

    Google Scholar 

  17. S.J. Wright, A path-following interior-point algorithm for linear and quadratic problems, Annals of Operations Research 62(1996)103–130.

    Article  Google Scholar 

  18. X. Xu, An O(√ nL)-iteration large-step infeasible path-following algorithm for linear programming, Department of Management Sciences, The University of Iowa, Iowa City, IA 52242, USA, August 1994.

    Google Scholar 

  19. Y. Ye and K. Anstreicher, On quadratic and O(√ nL) convergence of predictor-corrector algorithm for LCP, Mathematical Programming 62(1993)537–551.

    Article  Google Scholar 

  20. Y. Ye, O. Güler, R.A. Tapia and Y. Zhang, A quadratically convergent O(√nL)-iteration algorithm for linear programming, Mathematical Programming 59(1993)151–162.

    Article  Google Scholar 

Download references

Authors
  1. Florian A. Potra
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rongqin Sheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Potra, F.A., Sheng, R. A path following method for LCP withsuperlinearly convergent iteration sequence. Annals of Operations Research 81, 97–114 (1998). https://doi.org/10.1023/A:1018942131812

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1018942131812

Keywords

Search

Navigation