Abstract
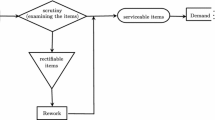
In this paper, we propose a model for the allocation of identical service facilities for restoring deteriorating production (e.g., batch chemical) processes. The problem is motivated by and solved for the new Dead Sea Works Ltd. magnesium plant. The production system consists of a number of identical production cells, each requiring a set of service tasks. The model determines both the optimal number of servers and the service rate allocated to each service task. The model takes into account the breakdown and repair processes for the service facilities. Thus, the optimal service rate is calculated and assigned according to the random number of available service facilities. Insightful results are provided by both analytical and numerical sensitivity analysis.
Similar content being viewed by others
References
M.S. Bazaraa and C.M. Shetty, Nonlinear Programming; Theory and Algorithms, Wiley, New York, 1993, ch. 5, pp. 184-195.
J.S. Benkoski, A survey of the search theory literature, Naval Research Logistics 38(1991)469-494
E. Fuchs, A. Mehrez, G. Rabinowitz and M. Vilchik, A decision theory approach to determine a capital joint venture structure: A manager view, Technical Paper, Ben Gurion University, 1995.
D. Granot and D. Zuckerman, Optimal scheduling and resource allocation in research and development projects, Management Science 37(1991)140-156.
E. Horowitz and S. Sahni, Fundamentals of Computer Algorithms, Computer Science Press, Rockville, MD, 1978, ch. 12, pp. 567-572.
P.T. Ittig, Planning service capacity when demand is sensitive to delay, Decision Sciences 25(1994)541-554.
M. Khouja, A. Mehrez and G. Rabinowitz, A nonlinear model for capacity allocation and throughput determination in cellular manufacturing systems, Engineering Optimization 23(1994)125-139.
M. Khouja, G. Rabinowitz and A. Mehrez, Optimal robot operation and selection using quality and output trade-off, The International Journal of Advanced Manufacturing Technology 10(1995)342-355.
E. Levner, Infinite-horizon scheduling algorithms for optimal search for hidden objects, International Transactions in Operational Research 1(1994)241-250
G. Rabinowitz, Imperfect inspection of multistage deteriorating production system, Technical Memorandum, I.E. Department, Ben Gurion University, 1995.
G. Rabinowitz and H. Emmons, Optimal and heuristic inspection schedules for multistage production systems, forthcoming in IIE Transactions (1996).
M.H. Rothkope, Scheduling independent tasks on parallel processors, Management Science 12(1966)437-448.
H.A. Taha, Operational Research, Maxwell Macmillan International Edition, New York, 1992, ch. 15, pp. 573-575.
J. Tanchoco, P. Egbelu and F. Taghaboni, Determination of the total number of vehicles in an AGV-based material transport system, Material Flow 4(1987)33-51
R.H. Wilhelm, Chemical Reactor Theory, A Review, Prentice-Hall, Englewood Cliffs, NJ, 1977, ch. 2, pp. 79-84.
D. Zuckerman, Optimal inspection policy for a multi-unit machine, Journal of Applied Probability 26(1989)543-551.
Rights and permissions
About this article
Cite this article
Shemesh, E., Rabinowitz, G. & Mehrez, A. Optimal capacity and operation of deteriorating chemical production service facilities. Annals of Operations Research 91, 205–225 (1999). https://doi.org/10.1023/A:1018945622552
Published:
Issue Date:
DOI: https://doi.org/10.1023/A:1018945622552