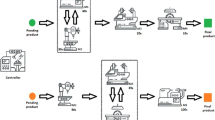
Abstract
The objective of this paper is a study of minimizing the maximum completion time min F max, or cycle time of the last job of a given family of jobs using flow shop heuristic scheduling techniques. Three methods are presented: minimize idle time (MIT); Campbell, Dudek and Smith (CDS); and Palmer. An example problem with ten jobs and five machines is used to compare results of these methods. A deterministic t-timed colored Petri net model has been developed for scheduling problem. An execution of the deterministic timed Petri net allows to compute performance measures by applying graph traversing algorithms starting from initial global state and going into a desirable final state(s) of the production system. The objective of the job scheduling policy is minimizing the cycle time of the last job scheduled in the pipeline of a given family of jobs. Three heuristic scheduling methods have been implemented. First, a sub-optimal sequence of jobs to be scheduled is generated. Second, a Petri net-based simulator with graphical user interface to monitor execution of the sequence of tasks on machines is dynamically designed. A deterministic t-timed colored Petri net model has been developed and implemented for flexible manufacturing systems (FMS). An execution of the deterministic timed Petri net into a reachability graph allows to compute performance measures by applying graph traversing algorithms starting from initial global state to a desirable final state(s) of the production system.
Similar content being viewed by others
References
Azzopardi, D. and Lloyd, S. (1994) Scheduling and through Petri net modeling. Proceedings of the 4th International Conference on Advanced Factory Automation, New York, United Kingdom.
Baker, K. R. (1974) Introduction to Sequencing and Scheduling, John Wiley & Sons, New York.
Banaszak, Z. (1994) Modeling of Manufacturing Systems. In Modern Manufacturing, Springer-Verlag, pp. 253-286.
Black, J. T. (1988) The design of manufacturing cells (step one to integrated manufacturing systems). Proceedings of Manufacturing International, Vol. III, Atlanta, GA, pp. 143-158.
Burbidge, J. L. (1988) Operation scheduling with GT and PBC. International Journal of Production Research, 26, 424-442.
Camus, H., Murgarza, J.-C., Teruel, E., Gentina, J.-C. and Silva, M. (1998) Scheduling Petri net models and structural analysis, in Borne, P., Ksouri, M. and Kamel, A. E. (eds) Vol. 3: Proceedings of CESA'98, Symposium on Industrial and Manufacturing Systems, Nabeul-Hammamet, Tunisia.
Carlier, J. and Chretienne, P. (1998) Timed Petri net schedules, in Rozenberg (ed), Advances in Petri nets, Springer-Verlag, pp. 62-84.
Desrochers, A. A. and Al-Jaar, R. Y. (1995) Applications of Petri nets in Manufacturing Systems, IEEE Press.
DiCesare, F., Harhalakis, G., Proth, J. M., Silva, M. and Vernadat, F. B. (1993) Practice of Petri nets in Manufacturing, Chapman & Hall.
Ezpeleta, J. and Colom, J. M. (1997) Automatic synthesis of colored Petri nets for the control of FMS. IEEE Transactions on Robotics and Automation, 13(3), 327-337.
Hatono, I., Yamagata, K. and Tamura, H. (1991) Modeling and on-line scheduling of flexible manufacturing systems using stochastic Petri nets. IEEE Transactions on Software Engineering, 17(2), 126-132.
Julia S., Valette R. and Tazza M. (1995) Computing a feasible schedule under a set of cyclic constraints. Proceedings of the 2nd International Conference on Industrial Automation, Nancy (France), CRAN, pp. 141-146.
Kattan, I. A. (1990) Designing flexible manufacturing cells using branch and bound method. International Journal of Production Research, 28(2), 325-336.
Kattan, I. A. (1997) Design and scheduling of hybrid multi-cell flexible manufacturing systems. International Journal of Production Research, 35(5), 1239-1257, Taylor & Francis, London, England.
King, J. R. and Nakarchai, V. (1982) Machine-component grouping formation in group technology: Review and extension. International Journal of Production Research, 20, 117-133.
Korbaa, O., Camus, H. and Gentina, J.-C. (1997) FMS cyclic scheduling with overlapping production cycles, in DiCesare, F., Silva, M. and Valette, R. (eds), Proceedings of the International Conference on Application and Theory of Petri Nets, Workshop on Manufacturing and Petri Nets, Toulouse, France, pp. 35-52.
Lee, DiCesare (1994) Scheduling flexible manufacturing systems using Petri nets and heuristic search. IEEE Transactions on Robotics and Automation, 10(2), 123-132.
Liljenvall, T. (2000) Benchmarking an algorithm for Petri net scheduling. Proceedings of the SMC'2000 International Conference, Nashville, Tennessee, IEEE Press.
Proth, J.-M., Wang, L. and Xie, X. (1997) A class of Petri nets for manufacturing system integration. IEEE Transactions on Robotics and Automation, 13(3), 318-325.
Radharamanan (1986) A heuristic algorithm for group scheduling. Proceedings of the 1986 IIE Fall Conference, Boston, Massachusetts.
Raju, K. R. and Chetty, O. V. K. (1993) Priority nets for scheduling flexible manufacturing systems. Journal of Manufacturing Systems, 12, 326-340.
Sule, D. R. (1997) Industrial Scheduling, PWS Publishing Company, Boston.
Villeda, R., Dudek, R. and Smith, M. L. (1988) Increasing the production rate of a just-in-time production system with variable operation times. International Journal of Production Research, 26(11), 1749-1768.
Zhou, M.-C. and Venkatesh, K. (1999) Modeling, Simulation, and Control of Flexible Manufacturing Systems, in Intelligent Control and Intelligent Automation, vol. 6, World Scientific Publishers.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Kattan, I., Mikolajczak, B., Kattan, K. et al. Minimizing cycle time and group scheduling, using Petri nets a study of heuristic methods. Journal of Intelligent Manufacturing 14, 107–121 (2003). https://doi.org/10.1023/A:1022243430453
Issue Date:
DOI: https://doi.org/10.1023/A:1022243430453