Abstract
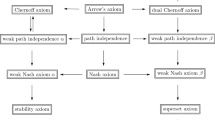
Set theoretic formulation of Arrow's theorem, viewedin light of a taxonomy of transitive relations,serves to unmask the theorem's understatedgenerality. Under the impress of the independenceof irrelevant alternatives, the antipode of ceteris paribus reasoning, a purported compilerfunction either breaches some other rationalitypremise or produces the effet Condorcet. Types of cycles, each the seeming handiwork of avirtual voter disdaining transitivity, arerigorously defined. Arrow's theorem erects adilemma between cyclic indecision anddictatorship. Maneuvers responsive theretoare explicable in set theoretic terms. None ofthese gambits rival in simplicity the unassistedescape of strict linear orderings, which, by virtueof the Arrow–Sen reflexivity premise, are notcaptured by the theorem. Yet these are therelations among whose n-tuples the effetCondorcet is most frequent. A generalization andstronger theorem encompasses these and all otherlinear orderings and total tierings. Revisions tothe Arrow–Sen definitions of `choice set' and`rationalization' similarly enable one to generalizeSen's demonstration that some rational choicefunction always exists. Similarly may onegeneralize Debreu's theorems establishing conditionsunder which a binary relation may be represented bya continuous real-valued order homomorphism.
Similar content being viewed by others
REFERENCES
Arrow, K. J.: 1963, Social Choice and Individual Values, 2nd ed., Yale University Press, New Haven, CT.
Arrow, K. J.: 1967, ‘Values and Collective Decision Making’ in Laslett, P. and Runciman, W. C., eds., Philosophy, Politics, and Society, Third Series, Basil Blackwell, Oxford, pp. 215-232, reprinted in Arrow 1983, pp. 59–77.
Arrow, K. J.: 1983, Collected Papers of Kenneth J. Arrow, I, Harvard University Press, Cambridge, MA.
Berkeley, G.: 1710, A Treatise Concerning the Principles of Human Knowledge.
Blair, D. H. and R. A. Pollak: 1982, ‘Acyclic Collective Choice Rules,’ Econometrica 50, 931-941.
Birkhoff, G.: 1948, Lattice Theory, 2nd ed., American Mathematical Society, New York.
Cantor, G.: 1895, ‘Beiträge zur Begründung der transfiniten Mengenlehre,’ Mathematische Annalen 46, 481-512, reprinted as Contributions to the Founding of the Theory of Transfinite Numbers, trans. Jourdain, P. E. B.: 1952, Open Court, La Salle, Il.
Condorcet, M. de: 1788, Essai sur la Contribution et les Fonction des Assemblées Provincials, trans. ‘On the Constitution and the Functions of Provincial Assemblies,’ in McLean, I. and Urken, A., eds: 1995, Classics of Social Choice, University of Michigan Press, Ann Arbor, MI, pp. 113-143.
Debreu, G.: 1954, ‘Representation of a Preference Ordering by a Numerical Function,’ in Thrall, R. M., Coombs, C. H., and Davis, R. L. eds, Decision Processes, Wiley, New York, pp. 159-65.
Debreu, G.: 1959, The Theory of Value, Wiley, New York.
Dummett, M.: 1984, Voting Procedures, Clarendon Press, Oxford.
Dummett, M.: 1998, ‘The Borda Count and Agenda Manipulation,’ Social Choice and Welfare 15, 289-296.
Fishburn, P. C.: 1972, Mathematics of Decision Theory, Mouton, The Hague.
Fishburn, P. C.: 1972, The Theory of Social Choice, Princeton University Press, Princeton, NJ.
Fishburn, P. C. and Gehrlein, W.: 1980, ‘The Paradox of Voting: Effects of Individual Preference and Intransitivity,’ Journal of Public Economics 14, 83-94.
Gehrlein, W.: 1983, ‘Condorcet's Paradox,’ Theory and Decision 15, 161-197.
Gibbard, A.: 1969, ‘Intransitive Social Indifference and the Arrow Dilemma,’ unpublished ms.
Gibbard, A.: 1973, ‘Manipulation of Voting Schemes: A General Result,’ Econometrica 41, 587-601.
Inman, R. P.: 1987, ‘Markets, Government, and the “New” Political Economy’ in Auerbach, A. J. and Feldstein, M. eds., Handbook of Public Economics, II, North-Holland, Amsterdam, pp. 647-777.
Kelly, J. S.: 1978, Arrow Impossibility Theorems, Academic Press, New York.
Kelly, J. S.: 1988, Social Choice Theory, Springer-Verlag, Berlin.
Menger, K.: 1951, ‘Probabilistic Theories of Relations,’ Proceedings of the National Academy of Sciences 37, 178-180.
Plott, C. R.: 1976, ‘Axiomatic Social Choice Theory,’ in Rowley, C. K., ed.: 1993, Social Choice Theory, I, Elgar, Aldershot, pp. 231-316.
Roberts, F. S., ed.: 1989, Applications of Combinatorics and Graph Theory to the Biological and Social Sciences, Springer-Verlag, New York.
Royden, H. L.: 1988, Real Analysis, 3rd edn, Macmillan, New York.
Russell, B.: 1920, Introduction to Mathematical Philosophy, 2nd edn, George Allen & Unwin, London.
Saari, D. G.: 1998, ‘Connecting and Resolving Sen's and Arrow's Theorems,’ Social Choice and Welfare 15, 239-261.
Sen, A. K.: 1966, ‘A Possibility Theorem on Majority Decisions,’ Econometrica 34, 491-499, reprinted in Sen 1997, pp. 109–17.
Sen, A. K.: 1970, Collective Choice and Social Welfare, Holden Day, San Francisco.
Sen, A. K.: 1986, ‘Social Choice Theory’ in Arrow, K. J. and Intriligator, M., eds, Handbook of Mathematical Economics, III, North-Holland, Amsterdam, pp. 1073-1181.
Sen, A. K.: 1997, Choice, Welfare, and Measurement, Harvard University Press, Cambridge, MA.
Taylor, A. D.: 1995, Mathematics and Politics, Springer-Verlag, New York.
Zwicker, W. S.: 1991, ‘The Voters' Paradox, Spin, and the Borda Count,’ Mathematical Social Sciences 22, 187-227.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Guenin, L.M. The Set Theoretic Ambit Of Arrow's Theorem. Synthese 126, 443–472 (2001). https://doi.org/10.1023/A:1005255924462
Issue Date:
DOI: https://doi.org/10.1023/A:1005255924462