Abstract
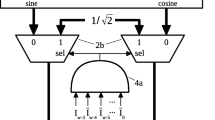
This paper presents a high-speed method for computing elementary functions using parallel table lookups and multi-operand addition. Increasing the number of tables and inputs to the multi-operand adder significantly reduces the amount of memory required. Symmetry and leading zeros in the table coefficients are used to reduce the amount of memory even further. This method has a closed-form solution for the table entries and can be applied to any differentiable function. For 24-bit operands, it requires two to three orders of magnitude less memory than conventional table lookups.
Similar content being viewed by others
References
V.K. Jain, G.E. Perez, and J.M. Wills, "Novel reciprocal and square-Root VLSI cell: Architecture and application to signal processing," International Conference on Acoustics; Speech and Signal Processing, Vol. 2, pp. 1201–1204, 1991.
V.K. Jain and L. Lin, "Square-root, reciprocal, sine/cosine, arctangent cell for signal and image processing," International Conference on Acoustics; Speech and Signal Processing, Vol. 2, pp. 521–524, 1994.
H. Kwan, R.L. Nelson, and E.E. Swartzlander, Jr., "Cascaded implementation of an iterative inverse-square-root algorithm with overflow lookahead," Proceedings of the 12th Symposium on Computer Arithmetic, pp. 114–123, 1995.
M. Zhang, S. Vassiliadis, and J.G. Delgado-Frias, "Sigmoid generators for neural computing using piecewise approximations," IEEE Transactions on Computers, Vol. 45, No. 9, pp. 1045–1050, 1996.
S. Mehrgardt, "Noise spectra of digital sine-generators using the table-lookup method," IEEE Transactions on Acoustics; Speech; and Signal Processing, Vol. 31, No. 4, pp. 1037–1039, 1983.
J.A. McIntosh and E.E. Swartzlander, Jr., "High-speed cosine generator," Conference record of the Twenty-Eighth Asilomar Conference on Signals; Systems and Computers, pp. 273–277, 1994.
J. McClellan, R. Schafer, and M. Yoder, DSP First: A Multimedia Approach, Prentice Hall, 1998.
D.M. Lewis, "114 MFLOPS logarithmic number system arithmetic unit for DSP applications," IEEE Journal of Solid-State Circuits, Vol. 30, No. 12, pp. 1547–1553, 1995.
H.-C. Shin, J.-A. Lee, and L.-S. Kim, "A minimized hardware architecture of fast Phong shader using taylor series approximation in 3D graphics," Proceedings of the International Conference on Computer Design. VLSI in Computers and Processors, pp. 286–291, 1998.
AltiVec Technology Programming Environments Manual. Motorola, Inc., 1998.
3DNow! Technology Manual, Nov. 1998, available at http:// www.amd.com/K6/k6docs/.
M.J. Flynn, "On division by functional iteration," IEEE Transactions on Computers, Vol. C-19, pp. 702–706, 1970.
S.F. Oberman and M.J. Flynn, "Division algorithms and implementations," IEEE Transactions on Computers, Vol. C-46, pp. 833–854, 1997.
D.D. Sarma and D.W. Matula, ""Measuring the accuracy of ROM reciprocal tables," Proceedings of the 11th Symposium on Computer Arithmetic, pp. 95–102, July 1993.
C.V. Ramamoorthy and J. Goodman, "Some properties of iterative square-rooting methods using high-speed multiplication," IEEE Transactions on Computers, Vol. C-21, pp. 837–847, 1972.
W. Cody and W. Waite, Software Manual for the Elementary Functions, Prentice-Hall, 1980.
J.F. Hart <nt>et al.</nt>, Computer Approximations, Wiley, 1968.
J.S. Walther, "A unified approach for elementary functions," Spring Joint Computer Conference, pp. 379–385, 1971.
J.-M. Muller, Elementary Functions: Algorithms and Implementation, Birkhauser, Boston, 1997.
T. Lynch, A. Ahmed, M.J. Schulte, T. Callaway, and R. Tisdale, "The K5 transcendental functions," Proceedings of the 12th Symposium on Computer Arithmetic, pp. 222–229, 1995.
W. Ferguson and T. Brightman, "Accurate and monotone approximations of some transcendental functions," Proceedings of the 10th Symposium on Computer Arithmetic, pp. 237–244, 1991.
Intel Pentium Processor Data Book, Intel Corporation, 1994.
M.J. Schulte and E.E. Swartzlander, Jr., "Hardware designs for exactly rounded elementary functions," IEEE Transactions on Computers, Vol. C-44, pp. 964–973, 1994.
P. Farmwald, "High bandwidth evaluation of elementary functions," Proceedings of the 5th Symposium on Computer Arithmetic, pp. 139–142, 1981.
I. Koren, Computer Arithmetic and Algorithms, Prentice Hall, 1993.
J.E.Volder, "The CORDIC trigonometric computing technique," IRE Transactions on Electronic Computers, Vol. EC-8, pp. 330–334, 1959.
G.H. Haviland and A.A. Tuszynski, "A CORDIC arithmetic processor," IEEE Transactions on Computers, Vol. C-29, pp. 68–79, 1980.
S.F. Hsiao and J.M. Delosme, "Householder CORIDC algorithms," IEEE Transactions on Computers, Vol. C-44, pp. 990–1000, 1995.
Sematech, Inc., The National Technology Roadmap for Semiconductors, 1997, available at http://notes.sematech.org/~ 97 pelec.htm.
A.R. Pelella <nt>et al.</nt>, "A 2–nanosecond access, 500 MHz, 288Kb SRAM macro," Symposium on VLSI Circuits, Digest of technical papers, pp. 309–318, 1995.
H. Hassler and N. Takagi, "Function evaluation by table look-up and addition," Proceedings of the 12th Symposium on Computer Arithmetic, pp. 10–16, 1995.
D.D. Sarma and D.W. Matula, "Faithful bipartite ROM reciprocal tables," Proceedings of the 12th Symposium on Computer Arithmetic, pp. 17–29, 1995.
S.F. Oberman, "Floating point division and square root algorithms and implementation in the AMD-K7 microprocessor," Proceedings of the 14th Symposium on Computer Arithmetic, pp. 106–115, April 1999, in press.
H. Kalish and J. Isaac <nt>(Eds.)</nt>, The AMD-K6 3D Processor, Abacus Software, 1998.
M.J. Schulte and J.E. Stine, "Symmetric bipartite tables for accurate function approximation," Proceedings of the 13th Symposium on Computer Arithmetic, pp. 175–183, 1997.
M.J. Schulte and J.E. Stine, "Accurate function approximations by symmetric table lookup and addition," 11th International Conference on Application-Specific Systems; Architectures; and Processors, pp. 144–153, 1997.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Stine, J.E., Schulte, M.J. The Symmetric Table Addition Method for Accurate Function Approximation. The Journal of VLSI Signal Processing-Systems for Signal, Image, and Video Technology 21, 167–177 (1999). https://doi.org/10.1023/A:1008004523235
Published:
Issue Date:
DOI: https://doi.org/10.1023/A:1008004523235