Abstract
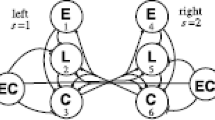
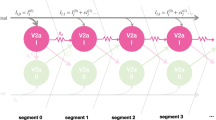
We present a simple stochastic model of two coupled phase oscillators and a method of fitting the model to experimental spike-train data or to sequences of burst times. We apply the method to data from lesioned isolated lamprey spinal cords. The remaining tracts at the lesion site are either regenerated medial tracts, regenerated lateral tracts, control medial tracts, or control lateral tracts. We show that regenerated tracts on average provide significantly weaker coupling than control tracts. We compare our model-dependent estimate of coupling strength to a measure of coordination based on the size of deflections in the spike-train cross-correlation histogram (CCH). Using simulated data, we show that our estimates are able to detect changes in coupling strength that do not change the size of deflections in the CCH. Our estimates are also more resistant to changes in the level of dynamic noise and to changes in relative oscillator frequency than is the CCH. In simulations with high levels of dynamic noise and in one experimental preparation, we are able detect significant coupling strength although there are no significant deflections in the CCH.
Similar content being viewed by others
References
Abeles M (1982) Quantification, smoothing, and confidence limits for single-units' histograms. J. Neurosci. Meth. 5:317–325.
Arnold L (1974) Stochastic Differential Equations: Theory and Applications. Wiley, New York.
Boxler P (1989) A stochastic version of center manifold theory. Probab. Th. Rel. Fields 83:509–545.
Buchanan JT (1992) Neural network simulations of coupled locomotor oscillators in the lamprey spinal cord. Biol. Cybern. 66:367–374.
Cohen AH, Wallén P (1980) The neuronal correlate of locomotion in fish. Exp. Brain Res. 41:11–18.
Cohen AH, Holmes PJ, Rand RH (1982) The nature of the coupling between segmental oscillators of the lamprey spinal generator for locomotion: A mathematical model. J. Math. Biol. 13:345–369.
Cohen AH, Baker MT, Dobrov TA (1989) Evidence for functional regeneration in the adult lamprey spinal cord following transection. Brain Res. 496:368–372.
Dennis JE, Schnabel RB (1983) Numerical Methods for Unconstrained Optimization and Nonlinear Equations. Prentice-Hall, Englewood Cliffs, NJ.
Ekeberg Ö (1993) A combined neuronal and mechanical model of fish swimming. Biol. Cybern. 69:363–374.
Ermentrout GB, Kopell N (1984) Frequency plateaus in a chain of weakly coupled oscillators, I. SIAM J. Math. Anal. 15:215–237.
Ermentrout GB, Kopell N (1991) Multiple pulse interactions and averaging in systems of coupled neural oscillators. J. Math. Biol. 29:195–217.
Fisher NI (1993) Statistical Analysis of Circular Data. Cambridge University Press, Cambridge.
Gard TC (1988) Introduction to Stochastic Differential Equations. Dekker, New York.
Grillner S, Matsushima T, Wadden T, Tegnér J, El Manira A, Wallén P (1993) The neurophysiological bases of undulatory locomotion in vertebrates. Semin. Neurosci. 5:17–27.
Harvey AC (1990) The Econometric Analysis of Time Series. MIT Press, Cambridge, MA.
Karr AF (1991) Point Processes and Their Statistical Inference. Dekker, New York.
Kopell N, Ermentrout GB (1986) Symmetry and phaselocking in chains of weakly coupled oscillators. Comm. Pure Appl. Math. 39:623–660.
Mellen N, Kiemel T, Cohen AH (1995) Correlational analysis of fictive swimming in the lamprey reveals strong functional intersegmental coupling. J. Neurophysiol. 73:1020–1030.
Neu JC (1979) Coupled chemical oscillators. SIAM J. Appl. Math. 37:307–315.
Perkel DH, Gerstein GL, Moore GP (1967) Neuronal spike trains and stochastic point processes. II. Simultaneous spike trains. Biophys. J. 7:419–440.
Rand RH, Holmes PJ (1980) Bifurcation of periodic motions in two weakly coupled van der Pol oscillators. Int. J. Non-Linear Mech. 15:387–399.
Sørensen M (1991) Likelihood methods for diffusions with jumps. In: NU Prabhu, IV Basawa, eds. Statistical Inference in Stochastic Processes. Dekker, New York. pp. 67–105.
Wallén P, Ekeberg Ö, Lansner A, Brodin L, Tråvén H, Grillner S (1992) A computer-based model for realistic simulations of neural networks. II. The segmental network generating locomotor rhythmicity in the lamprey. J. Neurophysiol. 68:1939–1950.
Williams TL (1992) Phase coupling by synaptic spread in chains of coupled neuronal oscillators. Science 258:662–665.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Kiemel, T., Cohen, A.H. Estimation of Coupling Strength in Regenerated Lamprey Spinal Cords Based on a Stochastic Phase Model. J Comput Neurosci 5, 267–284 (1998). https://doi.org/10.1023/A:1008835011799
Issue Date:
DOI: https://doi.org/10.1023/A:1008835011799