Skip to main content
SpringerLink
Log in

Spike-Frequency Adaptation of a Generalized Leaky Integrate-and-Fire Model Neuron

  • Published:
Journal of Computational Neuroscience Aims and scope Submit manuscript

Abstract

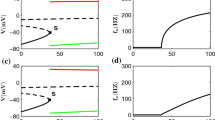
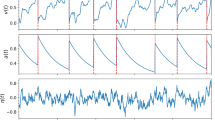
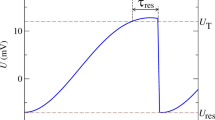
Although spike-frequency adaptation is a commonly observed property of neurons, its functional implications are still poorly understood. In this work, using a leaky integrate-and-fire neural model that includes a Ca2+-activated K+ current (I AHP), we develop a quantitative theory of adaptation temporal dynamics and compare our results with recent in vivo intracellular recordings from pyramidal cells in the cat visual cortex. Experimentally testable relations between the degree and the time constant of spike-frequency adaptation are predicted. We also contrast the I AHP model with an alternative adaptation model based on a dynamical firing threshold. Possible roles of adaptation in temporal computation are explored, as a a time-delayed neuronal self-inhibition mechanism. Our results include the following: (1) given the same firing rate, the variability of interspike intervals (ISIs) is either reduced or enhanced by adaptation, depending on whether the I AHP dynamics is fast or slow compared with the mean ISI in the output spike train; (2) when the inputs are Poisson-distributed (uncorrelated), adaptation generates temporal anticorrelation between ISIs, we suggest that measurement of this negative correlation provides a probe to assess the strength of I AHP in vivo; (3) the forward masking effect produced by the slow dynamics of I AHP is nonlinear and effective at selecting the strongest input among competing sources of input signals.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abbott LF, van Vreeswijk C (1993) Asynchronous states in networks of pulse-coupled oscillators. Phys. Rev. E 48:1483-1490.

    Google Scholar 

  • Ahmed B, Anderson JC, Douglas RJ, Martin KAC, Whitteridge D (1998) Estimates of the net excitatory currents evoked by visual stimulation of identified neurons in cat visual cortex. Cerebral Cortex 8:462-476.

    Google Scholar 

  • Amit DJ, Tsodyks MV (1991) Quantitative study of attractor neural networks retrieving at low spike rates. Network 2:259-294.

    Google Scholar 

  • Baranyi A, Szente MB, Woody CD (1993a) Electrophysiological characterization of different types of neurons recorded in vivo in the motor cortex of the cat. I. Patterns of firing activity and synaptic responses. J. Neurophysiol. 69:1850-1864.

    Google Scholar 

  • Baranyi A, Szente MB, Woody CD (1993b) Electrophysiological characterization of different types of neurons recorded in vivo in the motor cortex of the cat. II. Membrane parameters, action potentials, current-induced voltage responses and electrotonic structures. J. Neurophysiol. 69:1865-1879.

    Google Scholar 

  • Barkai E, Hasselmo ME (1994) Modulation of the input-output function of rat piriform cortex pyramidal cells. J. Neurophysiol. 72:644-658.

    Google Scholar 

  • Brunel N (2000) Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci.

  • Calvin W, Stevens CF (1968) Synaptic noise and other sources of randomness in motoneuron interspike intervals. J. Neurophysiol. 31:574-587.

    Google Scholar 

  • Connors BW, Gutnick MJ, Prince DA (1982) Electrophysiological properties of neocortical neurons in vitro. J. Neurophysiol. 48:1302-1320.

    Google Scholar 

  • Douglas RJ, Koch C, Mahowald M, Martin KAC, Suarez HH (1995) Recurrent excitation in neocortical circuits. Science 269:981-985.

    Google Scholar 

  • Ermentrout GB (1998) Linearization of F-I curve by adaptation. Neural Comput. 7:1721-1729.

    Google Scholar 

  • Foehring R, Lorenzon NM, Herron P, Wilson CJ (1991) Correlation of physiologically and morphologically identified neuronal types in human association cortex in vitro. J. Neurophysiol. 65:1825-1837.

    Google Scholar 

  • Gabbiani F, Koch C (1996) Coding of time-varying signals in spike trains of integrate-and-fire neurons with random threshold. Neural Comput. 8:44-66.

    Google Scholar 

  • Guckenheimer J, Harris-Warrick R, Peck J, Willms A (1997) Bifurcation, bursting, and spike frequency adaptation. J. Comput. Neurosci. 4:257-277.

    Google Scholar 

  • Hansel D, Mato G, Meunier C, Neltner L (1998) On numerical simulations of integrate-and-fire neural networks. Neural Comput. 10:467-484.

    Google Scholar 

  • Helmchen F, Imoto K, Sakmann B (1996) Ca2+ buffering and action potential-evoked Ca2+ signaling in dendrites of pyramidal neurons. Biophys. J. 70:1069-1081.

    Google Scholar 

  • Holden AV (1976) Models of the Stochastic Activity of Neurones. New York, Springer Verlag.

    Google Scholar 

  • Holt GR, Softky WR, Koch C, Douglas RJ (1996) Comparison of discharge variability in vitro and in vivo in cat visual cortex neurons. J. Neurophysiol. 75:1806-1814.

    Google Scholar 

  • Knight B (1972) Dynamics of encoding in a population of neurons. J. Gen. Physiol. 59:734-766.

    Google Scholar 

  • Koch C (1999) Biophysics of Computation. New York, Oxford University Press.

    Google Scholar 

  • Lancaster B, Zucker RS (1994) Photolytic manipulation of Ca2+ and the time course of slow, Ca2+-activated K+ current in rat hippocampal neurones. J. Physiol. Lond. 475:229-239.

    Google Scholar 

  • Lapicque L (1907) Recherches quantitatives sur l'excitation è lectrique des nerfs traitè e comme une polarisation. J. Physiol. Pathol. Gen. 9:620-635.

    Google Scholar 

  • Lapicque L (1927) L'excitabilitè en fonction du temps. Presses Universitaires de France, Paris.

    Google Scholar 

  • Lorenzon NM, Foehring RC (1992) Relationship between repetitive firing and afterhyperpolarizations in human neocortical neurons. J. Neurophysiol. 67:350-363.

    Google Scholar 

  • Madison DV, Nicoll RA (1984) Control of the repetitive discharge of rat CA1 pyramidal neurons in vitro. J. Physiol. 345:319-331.

    Google Scholar 

  • Markram H, Helm PJ, Sakmann B (1995) Dendritic calcium transients evoked by single back-propagating action potentials in rat neocortical pyramidal neurons. J. Physiol. Lond. 485:1-20.

    Google Scholar 

  • Mason A, Larkman A (1990) Correlations between morphology and electrophysiology of pyramidal neurons in slices of rat visual cortex. J. Neurosci. 10:1415-1428.

    Google Scholar 

  • McCormick DA, Connors BW, Lighthall JW, Prince DA(1985) Comparative electrophysiology of pyramidal and sparsely spiny stellate neurons of the neocortex. J. Neurophysiol. 54:782-805.

    Google Scholar 

  • McCormick DA, Williamson A (1989) Convergence and divergence of neurotransmitter action in human cerebral cortex. Proc. Natl. Acad. Sci. USA 86:8098-8102.

    Google Scholar 

  • Nicoll RA (1988) The coupling of neurotransmitter receptors to ion channels in the brain. Science 241:545-551.

    Google Scholar 

  • Pollack GS (1988) Selective attention in an insect auditory neuron. Spike-Frequency Adaptation with Stochastic Inputs 45 J. Neurosci. 8:2635-2639.

    Google Scholar 

  • Press WH, Flannery BP, Teukolsky SA, Vetterling WT (1989) Numerical Recipes. Cambridge University Press, Cambridge.

    Google Scholar 

  • Ricciardi LM (1977) Diffusion Processes and Related Topics in Biology. Springer-Verlag, Berlin.

    Google Scholar 

  • Rieke F, Warland D, de Ruyter van Steveninck R, Bialek W (1997) Spikes: Exploring the Neural Code. MIT Press, Cambridge, MAS.

    Google Scholar 

  • Rinzel J (1985) Bursting oscillations in an excitable membrane model, in ordinary and partial differential equations. Lecture Notes in Mathematics. Springer, New York. vol. 1151, pp. 304-316.

    Google Scholar 

  • Rinzel J (1987) A formal classification of bursting mechanisms in excitable systems. In: Gleason, AM, ed. Proceedings of the International Congress of Mathematicians. American Mathematical Society, Providence, RI. pp. 1578-1594.

    Google Scholar 

  • Schiller J, Helmchen F, Sakmann B (1995) Spatial profile of dendritic calcium transients evoked by action potentials in rat neocortical pyramidal neurones. J. Physiol. 487(3):583-600.

    Google Scholar 

  • Shadlen MN, Newsome WT (1994) Noise, neural codes and cortical organization. Curr. Opin. Neurobiol. 4:569-579.

    Google Scholar 

  • Shi WX, Rayport S (1994) GABA synapses formed in vitro by local axon collaterals of nucleus accumbens neurons. J. Neurosci. 14:4548-4560.

    Google Scholar 

  • Sobel EC, Tank DW (1994) In vivo Ca2+ dynamics in a cricket auditory neuron: An example of chemical computation. Science 263:823-826.

    Google Scholar 

  • Softky WR (1995) Simple codes versus efficient codes. Curr. Opin. Neurobiol. 5:239-247.

    Google Scholar 

  • Softky WR, Koch C (1993) The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci. 13:334-350.

    Google Scholar 

  • Somers D, Nelson S, Sur M (1995) An emergent model of orientation selectivity in cat visual cortical simple cells. J. Neurosci. 15:5448-5465.

    Google Scholar 

  • Stein RB (1965) A theoretical analysis of neuronal variability. Biophys. J. 5:173-195.

    Google Scholar 

  • Stein RB (1967) Some models of neuronal variability. Biophys. J. 7:37-68.

    Google Scholar 

  • Stemmler M, Usher M, Niebuhr E (1995) Lateral interaction in primary visual cortex: A model bridging physiology and psychophysics. Science 269:1977-1880.

    Google Scholar 

  • Svoboda K, Denk W, Kleinfeld D, Tank D (1997) In vivo dendritic calcium dynamics in neocortical pyramidal neurons. Nature 385:161-165.

    Google Scholar 

  • Tamás G, Buhl EH, Somogyi P (1997) Massive autaptic selfinnervation of GABAergic neurons in cat visual cortex. J. Neurosci. 17:6352-6364.

    Google Scholar 

  • Traub RD (1982) Simulation of intrinsic bursting in CA3 hippocampal neurons. Neurosci. 7:1233-1242.

    Google Scholar 

  • Treves A (1993) Mean-field analysis of neuronal spike dynamics. Network 4:259-284.

    Google Scholar 

  • Troyer TW, Miller KD (1997) Physiological gain leads to high ISI variability in a simple model of a cortical regular spiking cell. Neural Comput. 9:971-983.

    Google Scholar 

  • Tuckwell H (1988) Introduction to Theoretical Neurobiology. Cambridge University Press, Cambridge. vol. 2.

    Google Scholar 

  • van Vreeswijk C, Sompolinsky H (1996) Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274:1724-1726.

    Google Scholar 

  • Wang XJ (1998) Calcium coding and adaptive temporal computation in cortical pyramidal neurons. J. Neurophysiol. 79:1549-1566. Corrigendum, J. Neurophysiol. 79 (March 1998).

    Google Scholar 

  • Wang XJ, Rinzel J (1995) Oscillatory and bursting properties of neurons. In: Arbib MA, ed. The Handbook of Brain Theory and Neural Networks. MIT Press, Cambridge, MA. pp. 686-691.

    Google Scholar 

  • Wax N, ed. (1954) Selected Papers on Noise and Stochastic Processes. Dover, New York.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Volen Center for Complex Systems and Department of Physics, Brandeis University, Waltham, MA, 02454-9110

    Ying-Hui Liu & Xiao-Jing Wang

Authors
  1. Ying-Hui Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiao-Jing Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liu, YH., Wang, XJ. Spike-Frequency Adaptation of a Generalized Leaky Integrate-and-Fire Model Neuron. J Comput Neurosci 10, 25–45 (2001). https://doi.org/10.1023/A:1008916026143

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1008916026143

Search

Navigation