Universal Approximation Theorem for Interval Neural Networks

Abstract

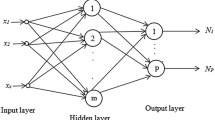
One of the main computer-learning tools is an (artificial) neural network (NN); based on the values y ^(p) of a certain physical quantity y at several points x ^(p)=(x ^(p)₁ ,...,x ^(p) _n ), the NN finds a dependence y = f(x₁,...,x _n ) that explains all known observations and predicts the value of y for other x = (x1,...,xn). The ability to describe an arbitrary dependence follows from the universal approximation theorem, according to which an arbitrary continuous function of a bounded set can be, within a given accuracy, approximated by an appropriate NN.

The measured values of y are often only known with interval uncertainty. To describe such situations, we can allow interval parameters in a NN and thus, consider an interval NN. In this paper, we prove the universal approximation theorem for such interval NN's.