Abstract
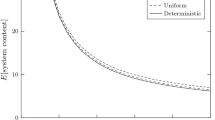
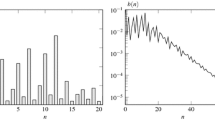
We propose a model to help a service provider manage a family of private-line telecommunication services. The model is a time-dependent network of infinite-server queues. The queueing network is used to model switching from one service to another. The relevant time scale is quite long: service lifetimes are measured in years, while service life cycles are measured in decades. To capture changing technology and customer preferences over this extended period, the model includes time-dependent new-connection rates, time-dependent switching rates and general time-dependent service-lifetime distributions for the different services. Because of the long service lifetimes, there is typically a significant time lag between the peak arrival rate and the peak expected number of customers receiving service. Thus sales and revenue do not move together; instead sales is a leading indicator of revenue in a service life cycle. The network structure reveals how the life cycles of different services are related. We show that it is possible to reasonably fit a version of this relatively complex model to data and then analyze the model to obtain useful descriptions of system dynamics.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
J. Abate and W. Whitt, Numerical inversion of probability generating functions, Operations Research Letters 12 (1992) 245-251.
J. Abate and W. Whitt, Numerical inversion of Laplace transforms of probability distributions, ORSA Journal on Computing 7 (1995) 36-43.
F.M. Bass, A new product growth model for consumer durables, Management Science 15 (1969) 215-227.
F.M. Bass, T.V. Krishnan and D.C. Jain, Why the Bass model fits without decision variables, Marketing Science 13 (1994) 203-223.
CCMI Guide to Networking Services, Interlata Private Line Services, Vol. 3 (Center for Communications Management Information, 1995).
R. Chatterjee and J. Eliashberg, The innovation diffusion process in a heterogeneous population: A micromodeling approach, Management Science 36 (1990) 1057-1079.
Data Communications Staff, The 1997 data communications market forecast, Data Communications Magazine 25(17) (1996) 54-64.
J.L. Davis, W.A. Massey and W. Whitt, Sensitivity to the service-time distribution in the non-stationary Erlang loss model, Management Science 41 (1995) 1107-1116.
R.D. Doverspike and V. Jha, Comparison of routing methods for DCS-switched networks, Interfaces 23 (1993) 21-34.
S.G. Eick, W.A. Massey and W. Whitt, The physics of the M t /G/ ∞queue, Operations Research 41 (1993) 731-742.
W. Feller, An Introduction to Probability Theory and Its Applications,Vol.I, 3rd ed. (Wiley, New York, 1968).
W. Feller, An Introduction to Probability Theory and Its Applications, Vol. II, 2nd ed. (Wiley, New York, 1971).
M.R. Garzia and C.M. Lockhart, Nonhierarchical communications networks: An application of compartmental modeling, IEEE Transactions on Communications 37 (1989) 555-564.
J.A. Jacques, Compartmental Analysis in Biology and Medicine, 2nd ed. (University of Michigan Press, Ann Arbor, 1985).
O.B. Jennings, A. Mandelbaum, W.A. Massey and W. Whitt, Server staffing to meet time-varying demand, Management Science 42 (1996) 1381-1394.
O.B. Jennings, W.A. Massey and C. McCalla, Optimal profit for leased lines services, in: Teletraffic Contributions for the Information Age, Proceedings of ITC 15, eds. V. Ramaswami and P.E. Wirth (Elsevier, Amsterdam, 1997) pp. 803-814.
J.F. Lawless, Statistical Models and Methods for Lifetime Data (Wiley, New York, 1982).
K.M. Malone, Dynamic Queueing Systems: Behavior and Approximations for Individual Queues, Ph.D. dissertation, Operations Research Center (Cambridge University, Cambridge, MA, 1995).
W.A. Massey, G.A. Parker and W. Whitt, Estimating the parameters of a nonhomogeneous Poisson process with linear rate, Telecommunication Systems 5 (1996) 361-388.
W.A. Massey and W. Whitt, Networks of infinite-server queues with nonstationary Poisson input, Queueing Systems 13 (1993) 183-250.
C.R. Master and L.R. Pamm, The digital data system launches a new era in data communications, Bell Laboratories Record 53 (1975) 420-426.
J.H. Matis and T.E. Wehrly, Generalized stochastic compartmental models with Erlang transit times, J. Pharmacokin. Biopharm. 18 (1990) 589-607.
P. Mertz and D. Mitchell, Aspects of data transmission using private line voice telephone channels, Bell System Technical Journal 36 (1957) 1451-1486.
J.A. Norton and F.M. Bass, A diffusion theory model of adoption and substitution for successive generations of high-technology products, Management Science 33 (1987) 1069-1086.
R. Nucho, Transient behavior of the Kendall birth-death process-applications to capacity expansion for special services, Bell System Technical Journal 60 (1981) 57-87.
M.D. Peterson, D.J. Bertsimas and A.R. Odoni, Decomposition algorithms for analyzing transient phenomena in multiclass queueing networks in air transportation, Operations Research 43 (1995) 995-1011.
G.W. Potts, Exploit your product's service life cycle, Harvard Business Review (September/October 1988) 4-7.
B.W. Schmeiser and M.R. Taaffe, Time-dependent queueing network approximations as simulation external control variates, Operations Research Letters 16 (1994) 1-9.
M. Segal and W. Whitt, A queueing network analyzer for manufacturing, in: Teletraffic Science for Cost-Effective Systems, Networks and Services, Proceedings of ITC 12, ed. M. Bonatti (North-Holland, Amsterdam, 1989) pp. 1146-1152.
D.R. Smith, A model for special-service circuit activity, Bell System Technical Journal 62 (1983) 2911-2934.
W. Whitt, The queueing network analyzer, Bell System Technical Journal 62 (1983) 2779-2815.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
McCalla, C., Whitt, W. A Time-Dependent Queueing-Network Model to Describe the Life-Cycle Dynamics of Private-Line Telecommunication Services. Telecommunication Systems 19, 9–38 (2002). https://doi.org/10.1023/A:1012239513006
Issue Date:
DOI: https://doi.org/10.1023/A:1012239513006