Abstract
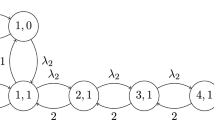
A ring of I cells rotates past I queues, carrying customers from their origins to their destinations. The system is modelled as a Markov chain, and the exact ergodicity conditions are given. They are shown to depend on the precise travel lengths distributions, that is, not only on their means. Ergodicity is proven through the stability analysis of the associated fluid limits. The arrivals distributions, which in the ergodicity conditions appear only through their means, are more subtly involved in the fluid limits behaviour, in that they determine the probabilities of random bifurcations that occur infinitely often in a simple system of I=2 queues.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. Asmussen, Applied Probability and Queues (Wiley, New York, 1987).
D.D. Botvitch and A.A. Zamyatin, Ergodicity of conservative communication networks, Rapport de recherche 1772, INRIA (October 1992).
E.G. Coffman, Jr., E.N. Gilbert, A.G. Greenberg, F.T. Leighton, P. Robert and A.L. Stolyar, Queues served by a rotating ring, Comm. Statist. Stochastic Models 11(3) (1995) 371-394.
J.G. Dai, On positive Harris recurrence of multiclass queueing networks: A unified approach via fluid limit models, Ann. Appl. Probab. 5(1) (1993) 49-77.
J.G. Dai and G. Weiss, Stability and instability of fluid models for re-entrant lines, Math. Oper. Res. 21(1) (1996) 115-134.
J.-F. Dantzer, M. Haddani and P. Robert, On the stability of a bandwidth packing algorithm, Probab. Engrg. Inform. Sci. 14 (2000) 57-79.
S.N. Ethier and T.G. Kurtz, Markov Processes (Characterization and Convergence) (Wiley, New York, 1986).
W. Feller, An Introduction to Probability Theory and Its Applications, Vols. 1/2, 3rd/2nd ed. (Wiley, New York, 1968/1971).
Y.P. Filonov, Ergodicity criteria for homogeneous discrete Markov chains, Ukrainian Math. J. 41(10) (1989) 1421-1422.
S. Foss and G. Last, Stability of polling systems with general service policies and with state dependent routing, Probab. Engrg. Inform. Sci. 12(1) (1998) 49-68.
V.A. Malyshev, Networks and dynamical systems, Adv. in Appl. Probab. 25 (1993) 140-175.
V.A. Malyshev and M.V. Menshikov, Ergodicity, continuity, and analyticity of countable Markov chains, Trans. Moskow Math. Soc. 1 (1981) 1-47.
A.N. Rybko and A.M. Stolyar, Ergodicity of stochastic processes describing the operation of open queueing networks, Problemy Peredachi Informatsii 28(3) (1992) 3-26.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Dantzer, JF., Dumas, V. Stability Analysis of the Cambridge Ring. Queueing Systems 40, 125–142 (2002). https://doi.org/10.1023/A:1014358600760
Issue Date:
DOI: https://doi.org/10.1023/A:1014358600760