Abstract
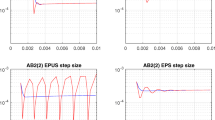
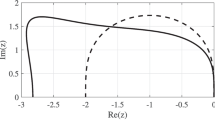
In this paper we consider stepsize selection in one class of Adams linear multistep methods for ordinary differential equations. In particular, the exact form of the local error for a variable step method is considered and a new class of direct approximations proposed. The implications of this approach are then discussed and illustrations provided with numerical results.
Similar content being viewed by others
References
G. Blesser, Eine effiziente Ordungs-und Schrittweitensteuerung unter Verwendung von Fehlerformeln für variable Gitter und ihre Realisierung in Mehrschrittverfahren von BDF-Typ, Diplomarbeit, University of Bonn (1986).
M. Calvo, D.J. Higham, J.I. Montijano and L. Rádez, Stepsize selection for tolerance proportionality in explicit Runge–Kutta codes, Adv. Comput. Math. 7 (1997) 361–382.
M. Calvo, J.I. Montijano and L. Rádez, On the change of stepsize in multistep codes, Numer. Algorithms 4 (1993) 283–304.
E. Eich, Projizierende Mehrschrittverfahren zur numerischen Lösung von Bewegungsgleichungen technischer Mehrkörpersysteme mit Zwangsbedingungen und Unstetigkeiten, Ph.D. thesis, University of Augsburg, Augsburg, Germany (1991).
I. Gladwell, L.F. Shampine and R.W. Brankin, Automatic section of the initial stepsize for an ODE solver, J. Comput. Appl. Math. 18 (1987) 175–192.
E. Hairer, S.P. Nørsett and G. Wanner, Solving Ordinary Differential Equations I – Non-stiff Problems (Springer, Heidelberg, 1987).
J. Hale, Theory of Functional Differential Equations, Applied Mathematical Sciences 3 (Springer, 1977).
F.T. Krogh, Changing stepsize in the integration of differential equations using modified divided differences, Lecture Notes in Mathematics 362 (1973) pp. 22–71.
L.F. Shampine and P. Bogacki, The effect of chaning the stepsize in linear multistep codes, SIAM J. Sci. Statist. Comput. 10(3) (1989) 1010–1023.
L.F. Shampine and M.K. Gordon, Computer Solution of Ordinary Differential Equations (Freeman, New York, 1975).
D.R. Willé, The numerical solution of delay-differential equations, Ph.D. thesis, University of Manchester, Manchester (1989).
D.R. Willé, New stepsize estimators for linear multistep methods, Numerical Analysis Report 247, Department of Mathematics, University of Manchester, Manchester (1994).
D.R. Willé and C.T.H. Baker, DELSOL – a numerical code for the solution of systems of delay-differential equations, Appl. Numer. Math. 9 (1992) 223–234.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Willé, D.R. Experiments in stepsize control for Adams linear multistep methods. Advances in Computational Mathematics 8, 335–344 (1998). https://doi.org/10.1023/A:1018960717197
Issue Date:
DOI: https://doi.org/10.1023/A:1018960717197