Abstract
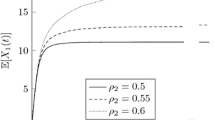
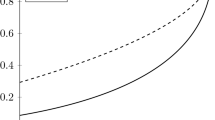
We consider the classical M/G/1 queue with two priority classes and the nonpreemptive and preemptive-resume disciplines. We show that the low-priority steady-state waiting-time can be expressed as a geometric random sum of i.i.d. random variables, just like the M/G/1 FIFO waiting-time distribution. We exploit this structures to determine the asymptotic behavior of the tail probabilities. Unlike the FIFO case, there is routinely a region of the parameters such that the tail probabilities have non-exponential asymptotics. This phenomenon even occurs when both service-time distributions are exponential. When non-exponential asymptotics holds, the asymptotic form tends to be determined by the non-exponential asymptotics for the high-priority busy-period distribution. We obtain asymptotic expansions for the low-priority waiting-time distribution by obtaining an asymptotic expansion for the busy-period transform from Kendall's functional equation. We identify the boundary between the exponential and non-exponential asymptotic regions. For the special cases of an exponential high-priority service-time distribution and of common general service-time distributions, we obtain convenient explicit forms for the low-priority waiting-time transform. We also establish asymptotic results for cases with long-tail service-time distributions. As with FIFO, the exponential asymptotics tend to provide excellent approximations, while the non-exponential asymptotics do not, but the asymptotic relations indicate the general form. In all cases, exact results can be obtained by numerically inverting the waiting-time transform.
Similar content being viewed by others
References
J. Abate and W. Whitt, Transient behavior of the M/M/1 queue via Laplace transforms, Adv. Appl. Probab. 20 (1988) 145–178.
J. Abate and W. Whitt, Simple spectral representations for the M/M/1 queue, Queueing Systems 3 (1988) 321–346.
J. Abate and W. Whitt, Approximations for the M/M/1 busy-period distribution, in: Queueing Theory and Its Applications - Liber Amicorium for J.W. Cohen, eds. O.J. Boxma and R. Syski (North-Holland, Amsterdam, 1988) pp. 149–191.
J. Abate and W. Whitt, The Fourier-series method for inverting transforms of probability distributions, Queueing Systems 10 (1992) 5–88.
J. Abate and W. Whitt, Solving probability transform functional equations for numerical inversion, Oper. Res. Lett. 12 (1992) 275–281.
J. Abate and W. Whitt, Transient behavior of the M/G/1 workload process, Oper. Res. 42 (1994) 750–764.
J. Abate and W. Whitt, A heavy-traffic expansion for the asymptotic decay rates of tail probabilities in multi-channel queues, Oper. Res. Lett. 15 (1994) 223–230.
J. Abate and W. Whitt, Limits and approximations for the busy-period distribution in single-server queues, Probab. Engrg. Inform. Sci. 9 (1995) 581–602.
J. Abate and W. Whitt, An operational calculus for probability distributions via Laplace transforms, Adv. Appl. Probab. 28 (1996) 75–113.
J. Abate and W. Whitt, Limits and approximations for the M/G/1 LIFO waiting-time distribution, Oper. Res. Lett., to appear.
J. Abate, G.L. Choudhury and W. Whitt, Waiting time tail probabilities in queues with long-tail service-time distributions, Queueing Systems 16 (1994) 311–338.
J. Abate, G.L. Choudhury and W. Whitt, Exponential approximations for tail probabilities in queues, I: waiting times, Oper. Res. 43 (1995) 885–901.
J. Abate, G.L. Choudhury and W. Whitt, Calculating the M/G/1 busy-period density and LIFO waiting-time distribution by direct numerical transform inversion, Oper. Res. Lett. 18 (1995) 113–119.
J. Abate, G.L. Choudhury and W. Whitt, Exponential approximations for tail probabilities in queues, II: Sojourn time and workload, Oper. Res. 44 (1996) 758–763.
J. Abate, G.L. Choudhury and W. Whitt, On the Laguerre method for numerically inverting Laplace transforms, INFORMS J. Comput. 8 (1996) 413–427.
J. Abate, G.L. Choudhury and W. Whitt, Numerical inversion of multidimensional Laplace transforms by the Laguerre method, Perf. Eval., to appear.
J. Abate, M. Kijima and W. Whitt, Decompositions of the M/M/1 transition function, Queueing Systems 9 (1993) 323–336.
S. Asmussen, Applied Probability and Queues (Wiley, New York, 1987).
S. Asmussen and J.L. Teugels, Convergence rates for M/G/1 queues and ruin problems with heavy tails, Adv. Appl. Probab., to appear.
K.B. Athreya and P.E. Ney, Branching Processes (Springer, Berlin, 1972).
A.W. Berger and W. Whitt, Effective bandwidths for waiting times with priorities, in preparation.
N.H. Bingham, C.M. Goldie and J.L. Teugels, Regular Variation (Cambridge Univ. Press, Cambridge, England, 1989).
A.A. Borovkov, Stochastic Processes in Queueing Theory (Springer, New York, 1976).
C.S. Chang and J.A. Thomas, Effective bandwidths in high-speed digital networks, IEEE J. Sel. Areas Commun. 13 (1995) 1091–1100.
V.P. Chistyakov, A theorem on sums of independent positive random variables and its applications to branching processes, Theory Probab. Appl. 9 (1964) 640–648.
G.L. Choudhury and W. Whitt, Computing distributions and moments in polling models by numerical transform inversion, Perf. Eval. 25 (1996) 267–292.
G.L. Choudhury, D.M. Lucantoni and W. Whitt, Multidimensional transform inversion with applications to the transient M/G/1 queue, Ann. Appl. Probab. 4 (1994) 719–740.
J. Chover, P. Ney and S. Wainger, Functions of probability measures, J. Analyse Math. 26 (1973) 255–302.
J. Chover, P. Ney and S. Wainger, Degeneracy properties of subcritical branching process, Ann. Probab. 1 (1973) 663–673.
J.W. Cohen, The Single Server Queue, revised ed. (North-Holland, Amsterdam, 1982).
D.R. Cox and W.L. Smith, Queues (Methuen, London, 1961).
A. De Meyer and J.L. Teugels, On the asymptotic behavior of the distribution of the busy period and the service time in M/G/1, Adv. Appl. Probab. 17 (1980) 802–813.
G. de Veciana, G. Kesidis and J. Walrand, Resource management in wide-area ATM networks using effective bandwidths, IEEE J. Sel. Areas Commun. 13 (1995) 1081–1090.
G. Doetsch, Introduction to the Theory and Applications of the Laplace Transformation (Springer, New York, 1974).
N. Duffield, Exponents for the tails of distributions in some polling models, Queueing Systems, to appear.
D.G. Duffy, Transform Methods for Solving Partial Differential Equations (CRC Press, Boca Raton, FL, 1994).
A. Erdélyi, Asymptotic Expansions (Dover, New York, 1956).
W. Feller, An Introduction to Probability Theory and its Applications, Vol. II, 2nd edn. (Wiley, New York, 1971).
L. Flatto, The waiting time distribution for random order of service, Ann. Appl. Probab., to appear.
D.P. Gaver, Jr., A waiting line with interrupted service, including priorities, J. Roy. Statist. Soc. Ser. B 25 (1962) 73–90.
D.P. Heyman and M.J. Sobel, Stochastic Models in Operations Research, Vol. I (McGraw-Hill, New York, 1982).
J.M. Harrison, A limit theorem for priority queues in heavy traffic, J. Appl. Probab. 10 (1973) 907–912.
E. Hille, Analytic Function Theory, Vol. I (Blaisdell, Waltham, MA, 1959).
O. Kella, Parallel and tandem fluid networks with dependent Lévy inputs, Ann. Appl. Probab. 3 (1993) 682–695.
D.R. Miller, Computation of steady-state probabilities for M/M/1 priority queues, Oper. Res. 29 (1981) 945–958.
F.W.J. Olver, Asymptotics and Special Functions (Academic Press, New York, 1974).
A.G. Pakes, On the tails of waiting-time distributions, J. Appl. Probab. 12 (1975) 555–564.
A. Shwartz and A. Weiss, Large Deviations for Performance Analysis (Chapman and Hall, London, 1995).
D. Stoyan, Comparison Methods for Queues and Other Stochastic Models (Wiley, Chichester, 1983).
W.G.L. Sutton, The asymptotic expansion of a function whose operational equivalent is known, J. London Math. Soc. 9 (1934) 131–137.
B. Van Der Pol and H. Bremmer, Operational Calculus (Cambridge Press, 1955; reprinted Chelsea, New York, 1987).
A. Washburn, A particular two-priority queue, Oper. Res. 18 (1970) 1760–1764.
W. Whitt, Weak convergence theorems for priority queues: preemptive-resume discipline, J. Appl. Probab. 8 (1971) 74–94.
R.W. Wolff, Stochastic Modeling and the Theory of Queues (Prentice-Hall, Englewood Cliffs, NJ, 1989).
Rights and permissions
About this article
Cite this article
Abate, J., Whitt, W. Asymptotics for M/G/1 low-priority waiting-time tail probabilities. Queueing Systems 25, 173–233 (1997). https://doi.org/10.1023/A:1019104402024
Issue Date:
DOI: https://doi.org/10.1023/A:1019104402024