Abstract
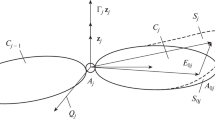
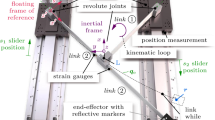
This paper relates recent results obtained in the field of modelling and control of flexible link manipulators and proposes an investigation of the problem raised by this type of systems (at least in the planar case). First, adopting the modal floating frame approach and the Newton–Euler formalism, we propose an extension of the models for control to the case of fast dynamics and finite deformations. This dynamic model is based on a nonlinear generalisation of the standard Euler–Bernoulli kinematics. Then, based on the models recalled we treat the end-effector tracking problem for the one-link case as well as for the planar multi-link case. For the one-link system, we propose two methods, the first one is based on causal stable inversion of linear non-minimum phase model via output trajectory planning. The other one is an algebraic scheme, based on the parametrization of linear differential operators. For the planar multi-link case the control law proposed is based on causal stable inversion over a bounded time domain of nonlinear non-minimum phase systems. Numerical tests are presented together with experimental results, displaying the well behaved of these approaches.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Agrawal, O. P. and Shabana, A.: 1985, Dynamical analysis of multibody systems systems using component modes, Comput. Struct. 21, 1303–1312.
Aoustin, Y., Chevallereau, C., Glumineau, A., and Moog, C. H.: 1994, Experimental results for the end-effector control of a single flexible robotic arm, IEEE Trans. Control Systems Technology 2, 371–381.
Arnold, V. I.: 1988, Mathematical Methods in Classical Mechanics, Springer, New York.
Ascher, U., Christiansen J., and Russell R. D.: 1981, Collocation software for boundary-value ODEs, ACM Trans. Math. Software 7(2), 209–222.
Balas, M. J.: 1982, Trends in large space structure control theory: Fondest hopes, wildest dreams, IEEE Trans. Automat. Control 27(3), 522–535.
Bayo, E.: 1987, A finite-element approach to control the end-point motion of a single link flexible robot, J. Robotic Systems 4, 63–75.
Bayo, E.: 1988, Computed torque for the position control of open-chain flexible robots, in: IEEE Internat. Conf. on Robotics and Automation, Philadelphia, pp. 316–321.
Bayo, E. and Moulin, H.: 1989, An efficient computation of the inverse dynamics of flexible manipulators in the time domain, in: IEEE Internat. Conf. on Robotics and Automation, pp. 710–715.
Benosman, M. and Le Vey, G.: 2000a, End-effector motion planning for one-link flexible robot, in: IFAC, Symposium on Robot Control, Vol. 2, pp. 561–566.
Benosman, M. and Le Vey, G.: 2000b, Exact articular trajectory tracking for a one-link flexible manipulator: An approach through the parametrization of differential operators, in: 31th Internat. Symposium on Robotics (ISR2000), Montréal, Canada, pp. 493–498.
Benosman, M. and Le Vey, G.: 2000c, Accurate trajectory tracking of flexible arm end-point, in: IFAC Symposium on Robot Control, Vol. 2, pp. 569–572.
Benosman, M. and Le Vey, G.: 2001a, Stable inversion of SISO non-minimum phase linear dynamic through output planning: An experimental application to the one-link flexible manipulator, Technical Report 01/3/AUTO, Ecole des Mines de Nantes.
Benosman, M. and Le Vey, G.: 2001b, Output trajectory tracking for a particular class of nonlinear non-minimum phase systems, Technical Report 01/6/AUTO, Ecole des Mines de Nantes.
Benosman, M. and Le Vey, G.: 2001c, Model inversion for a particular class of nonlinear nonminimum phase systems: An application to the two-link flexible manipulator, in: 40th IEEE CDC, pp. 1174–1180.
Book, W. J.: 1984, Recursive Lagrangian dynamics of flexible manipulators arms, Internat. J. Robotics Res. 3, 87–101.
Boyer, F.: 1994, Contribution à la modélisation et à la commande dynamique des robots flexibles, PhD Thesis, Paris 6 University.
Boyer F. and Coiffet, P.: 1996a, Generalisation of Newton–Euler model for flexible manipulators, J. Robotic Systems 13(1), 11–24.
Boyer, F. and Coiffet, P.: 1996b, Symbolic modelling of a flexible manipulator via assembling of its generalized Newton–Euler model, J. Mechanism Machine Theory 31, 45–56.
Boyer, F. and Khalil, W.: 1998, An efficient calculation of flexible manipulator inverse dynamics, Internat. J. Robotics Res. 17(3), 282–293.
Boyer, F. and Khalil, W.: 1999, Kinematic model of a multi-beam structure undergoing large elastic displacement and rotations. Part one: Model of an isolated beam, J. Mechanism Machine Theory 34, 205–222.
Boyer, F., Glandais, N., and Khalil, W.: 2002, Flexible multibody dynamics based on a nonlinear Euler–Bernoulli kinematics, Internat. J. Numer. Methods Engrg. 54, 27–59.
Boyer, F. and Primault, D.: 2001a, Poincaré's equations and multibody dynamics, part I: Mathematical fundamentals, Technical Report 01/1/AUTO, Ecole des Mines de Nantes.
Boyer, F. and Primault, D.: 2001b, Poincare's equations and multibody dynamics, part II: Application to multibody dynamics, Technical Report 01/2/AUTO, Ecole des Mines de Nantes.
Brokett, R.W., Stokes, A., and Park, F.: 1993, A geometrical formulation of the dynamical equations describing kinematic chains, IEEE Internat. Conf. on Robotics and Automation, pp. 637–641.
Canavin, J. R. and Likins, P. W.: 1977, Floating reference frames for flexible spacecrafts, J. Spacecraft 14(12), 724–732.
Cardona, A. and Géradin, M.: 1988, A beam finite element nonlinear theory with finite rotations, Internat. J. Numer. Methods Engrg. 26, 2403–2438.
Christoforoua, E. G. and Damaren, C. J.: 2000, The control of flexible-link robots manipulating large payloads: Theory and experiments, J. Robotic Systems 17(5), 255–271.
Damaren, C. J.: 1995, Passivity analysis for flexible multilink space manipulators, J. Guidance Control Dynamics 18(2), 272–279.
D'Eleuterio, G. M. T.: 1992, Dynamics of an elastic multibody chain. Part C-recusive dynamics, J. Dyn. Stability Systems 7(2), 61–89.
De Luca, A. and Siciliano, B.: 1989, Trajectory control of a nonlinear one link flexible arm, Internat. J. Control 50(5), 1699–1715.
De Luca, A. and Siciliano, B.: 1991, Closed-form dynamic model of planar multilink lightweight robots, IEEE Trans. Systems Man Cybernet.
De Luca, A., Panzieri, S., and Ulivi, G.: 1998, Stable inversion control for flexible link manipulators, in: IEEE Internat. Conf. of Robotics and Automation, Leuven, Belgium, pp. 799–801.
Fliess, M., Sira-Ramirez, H., and Marquez, R.: 1998, Perspectives in Control, Theory and Applications, Chapter: Control design methodologies. Regulation of non-minimum phase outputs: A flatness based approach, pp. 143–163.
Hastings, G. G. and Book, W. J.: 1986, Verification of linear dynamic model for flexible robotic manipulators, in: IEEE Internat. Conf. on Robotics and Automation, New York, pp. 1024–1029.
Hughes, P. C. and Sincarsin, G. B.: 1989, Dynamics of elastic multibody chains: Part B – Global dynamics, Dyn. Stability Systems 4, 227–243.
Khalil, H.: 1992, Nonlinear Linear Systems, Macmillan, New York.
Marsden, J. E. and Ratiu, T. S.: 1999, Introduction to Mechanics and Symmetry, Springer, New York.
Meirovitch, L.: 1989, Dynamics and Control of Structures, Wiley, New York.
Paden B., Chen, D., Ledesma, R., and Bayo, E.: 1993, Exponentially stable tracking control for mulitjoint flexible-link manipulators, J. Guidance Control Dynamics 115, 53–59.
Poincaré, H.: 1901, Sur une forme nouvelle des équations de la mécanique, C. R. Acad. Sci. Paris 132, 369–371.
Pommaret, J. F.: 1994, Partial Differential Equations and Group Theory, Mathematics and its Applications, Vol. 293, Kluwer Academic, Dordrecht.
Schmitz, E.: 1985, Experiments on the end-point position control of a very flexible one-link manipulator, PhD Thesis, Standford University.
Shabana, A. A.: 1989, Dynamics of Multibody Systems, Wiley, New York.
Sharf, I.: 1996, Geometrically non-linear beam element for dynamics of multibody systems, Internat. J. Numer. Methods Engrg. 39, 763–786.
Sharf, I. and Damaren, C.: 1992, Simulation of flexible-link manipulators: Basis functions and nonlinear terms in the motion equations, in: IEEE Internat. Conf. on Robotics and Automation, Nice, France, pp. 1956–1962.
Simo, J. C. and Vu-Quoc L.: 1988, On the dynamics in space of rods undergoing large motions – A geometrically exact approach, Comput. Methods Appl. Mech. Engrg. 66, 125–161.
Spivak, M.: 1976, Differential Geometry, Perish, Houston.
Theodor, R. J. and Ghosal, A.: 1995, Comparison of the assumed modes and finite elements models for flexible multilink manipulators, Internat. J. Robotics Res. 14(2), 91–111.
Wehage, R. A. and Haug, E. J.: 1982, Generalized coordinate partitioning for dimension reduction in analysis of constrained dynamic systems, J. Mech. Design. 104.
Zhao, H. and Chen, D.: 1998, Tip trajectory tracking for multilink flexible manipulators using stable inversion, J. Guidance Control Dynamics 21(2), 314–320.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Benosman, M., Boyer, F., Le Vey, G. et al. Flexible Links Manipulators: from Modelling to Control. Journal of Intelligent and Robotic Systems 34, 381–414 (2002). https://doi.org/10.1023/A:1019639517064
Issue Date:
DOI: https://doi.org/10.1023/A:1019639517064