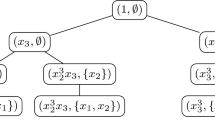
Abstract
An algorithm for computation of Janet bases for toric ideals, which is based on the structure of the Janet tree, is suggested. The algorithm can be applied, in particular, to solving integer programming problems with the use of algorithmic ideas by Conti and Traverso.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.REFERENCES
Conti, P. and Traverso, C., Buchberger Algorithm and Integer Programming, Proc. AAECC-9, LNCS, 1991, vol. 539, pp. 130-139.
Pottier, L., Groebner Bases of Toric Ideals, Rapport de recherche 2224, 1997, INRIA, Sophia Antipolis.
Di Biase, F. and Urbanke, R., An Algorithm to Calculate the Kernel of Certain Polynomial Ring Homomorphisms, Exp. Math., 1995, vol. 4, pp. 227-234.
Hosten, S. and Sturmfels, B., GRIN: An Implementation of Groebner Basis for Integer Programming, Integer Programming and Combinatorial Optimization, LNCS, 1995, vol. 920, pp. 267-276.
Bigatti, A.M., La Scala, R., and Robbiano, L., Computing Toric Ideals, J. Symbol. Comp., 1999, vol. 27, pp. 351-365.
Zharkov, A.Yu. and Blinkov, Yu.A., Involutive Systems of Algebraic Equations, Programmirovanie, 1994, no. 1, pp. 53-56.
Apel, J., Gröbner Approach to Involutive Bases, J. Symbol. Comp., 1995, vol. 19, pp. 441-458.
Gerdt, V.P. and Blinkov, Yu.A., Involutive Bases of Polynomial Ideals, Math. Comp. Simul., 1998, vol. 45, pp. 519-542.
Gerdt, V.P. and Blinkov, Yu.A., Involutive Divisions of Monomials, Programmirovanie, 1998, no. 6, pp. 22-24.
Chen, Yu-Fu and Gao, X.-Sh., Vector Representation of Involutive Divisions, Mathematics-Mechanization Research Preprints, Beijing, 1999, no. 18, pp. 9-22.
Gerdt, V.P., Blinkov, Yu.A., and Yanovich, D.A., Construction of Janet Bases II. Polynomial Bases, Proc. of CASC'01, Berlin: Springer, 2001, pp. 249-263.
Blinkov, Yu.A., Method of Separative Monomials for Involutive Divisions, Programmirovanie, 2001, no. 3, pp. 43-45.
Gerdt, V.P., Yanovich, D., and Blinkov, Yu.A., Fast Search for the Janet Divisor, Programmirovanie, 2001, no. 1, pp. 32-36.
Gerdt, V.P., Blinkov, Yu.A., and Yanovich, D.A., Construction of Janet Bases I. Monomial Bases, Proc. of CASC'01, Berlin: Springer, 2001, pp. 233-247.
Janet, M., Leçons sur les Systèmes d'Equations aux Dérivées Partielles, Cahiers Scientifiques, IV, Paris: Gauthier-Villars, 1929.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Blinkov, Y.A. Computation of Janet Bases for Toric Ideals. Programming and Computer Software 28, 290–292 (2002). https://doi.org/10.1023/A:1020264212943
Issue Date:
DOI: https://doi.org/10.1023/A:1020264212943