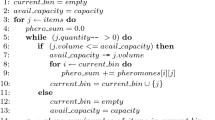Abstract
Ant Colony Optimization (ACO) is a metaheuristic used to solve combinatorial optimization problems. As with other metaheuristics, like evolutionary methods, ACO algorithms often show good optimization behavior but are slow when compared to classical heuristics. Hence, there is a need to find fast implementations for ACO algorithms. In order to allow a fast parallel implementation, we propose several changes to a standard form of ACO algorithms. The main new features are the non-generational approach and the use of a threshold based decision function for the ants. We show that the new algorithm has a good optimization behavior and also allows a fast implementation on reconfigurable processor arrays. This is the first implementation of the ACO approach on a reconfigurable architecture. The running time of the algorithm is quasi-linear in the problem size n and the number of ants on a reconfigurable mesh with n 2 processors, each provided with only a constant number of memory words.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
A. Bauer, B. Bullnheimer, R. F. Hartl, and C. Strauss, “Minimizing total tardiness on a single machine using ant colony optimization,” Central European Journal of Operations Research, vol. 8, pp. 125–141, 2000.
M. L den Besten, T. Stützle, and M. Dorigo, “Ant colony optimization for the total weighted tardiness problem,” in Parallel Problem Solving from Nature: 6th International Conference, M. Schoenauer et al. (eds.), Springer: Berlin, LNCS, vol. 1917, pp. 611–620, 2000.
K. Bondalapati and V. K. Prasanna, “Reconfigurable meshes: Theory and practice,” in Proc. Recon-figurable Architectures Workshop, R. W. Hartenstein and Viktor K. Prasanna (eds.), April 1, 1997, Geneva, Switzerland, ITpress Verlag: Bruchsal.
B. Bullnheimer, G. Kotsis, and C. Strauss, “Parallelization strategies for the ant system,” in High Performance Algorithms and Software in Nonlinear Optimization, R. De Leone, A. Murli, P. Pardalos, and G. Toraldo (eds.), Series: Applied Optimization, Kluwer: Dordrecht, vol. 24, pp. 87–100, 1998.
R. K. Congram, C. N. Potts, and S. L. van de Velde, “An iterated dynasearch algorithm for the singlemachine total weighted tardiness scheduling problem,” Working Paper, University of Southampton, UK, 1998.
M. Dorigo and G. Di Caro, “The ant colony optimization meta-heuristic,” in New Ideas in Optimization, D. Corne, M. Dorigo, F. Glover (eds.), McGraw-Hill: London, pp. 11–32, 1999.
M. Dorigo and L. M. Gambardella, “Ant colonies for the QAP,” Technical Report IDSIA-4-97, IDSIA, Lugano, 1997.
M. Dorigo and L. M. Gambardella, “Ant colony system: A cooperative learning approach to the traveling salesman problem,” IEEE Transactions on Evolutionary Computation, vol. 1, pp. 53–66, 1997.
L. M. Gambardella, E. Taillard, and M. Dorigo, “Ant colonies for the quadratic assignment problem,” Journal of the Operational Research Society, vol. 50, pp. 167–176, 1999.
S. Hartmann, and R. Kolisch, “Experimental evaluation of state-of-the-art heuristics for the resource-constrained project scheduling problem,” European Journal of Operational Research, vol. 127, pp. 394–407, 2000.
V. Maniezzo, “Exact and approximate nondeterministic tree-search procedures for the quadratic assignment problem,” INFORMS Journal on Computing, vol. 11, pp. 358–368, 1999.
V. Maniezzo, A. Colorni, and M. Dorigo, “The ant system applied to the quadratic assignment problem,” Tech. Rep. IRIDIA/94-28, Université Libre de Bruxelles, Belgium, 1994.
V. Maniezzo and A. Colorni, “The ant system applied to the quadratic assignment problem,” IEEE Transactions on Knowledge and Data Engineering, vol. 11, pp. 769–778, 1999.
D. Merkle and M. Middendorf, “An ant algorithm with global pheromone evaluation for scheduling a single machine,” Applied Intelligence, to appear.
D. Merkle, M. Middendorf, and H. Schmeck, “Ant colony optimization for resource-constrained project scheduling,” in Proc. of the Genetic and Evolutionary Computation Conference (GECCO-2000), D. Whitley et al. (eds.), Morgan Kaufmann, pp. 893–900, 2000.
N. Meuleau and M. Dorigo, “Ant Colony Optimization and Stochastic Gradient Descent,” Tech. Rep. IRIDIA/2000-36, Université Libre de Bruxelles, Belgium, 2000.
R. Michels and M. Middendorf, “An ant system for the shortest common supersequence problem,” in New Ideas in Optimization, D. Corne, M. Dorigo, and F. Glover (eds.) McGraw-Hill, pp. 51–61, 1999.
M. Middendorf, “Bit-summation on the reconfigurable mesh,” in Parallel and Distributed Computing, Proc. of the 11 IPPS/SPDP'99 Workshops, 6th Reconfigurable Architectures Workshop RAW-99, J. Rolim et al. (eds.), Springer: Berlin, LNCS, vol. 1586, pp. 625–633, 1999.
M. Middendorf, F. Reischle, and H. Schmeck, “Multi colony ant algorithms,” Journal of Heuristics, vol. 8, pp. 305–320, 2002.
R. Miller, V. K. Prasanna-Kumar, D. I. Reisis, and Q. F. Stout, “Parallel computations on reconfigurable meshes,” IEEE Trans. Comput., vol. 42, pp. 678–692, 1993.
K. Nakano and K. Wada, “Integer summing algorithms on reconfigurable meshes,” Theoret. Comput. Sci., vol. 197, pp. 57–77, 1998.
T. Stützle, “An ant approach for the flow shop problem,” in Proc. 6th European Congress on Intelligent Techniques & Soft Computing (EUFIT '98), Verlag Mainz: Aachen, vol. 3, pp. 1560–1564, 1998.
T. Stützle and M. Dorigo, “ACO algorithms for the quadratic assignment problem,” in New Ideas in Optimization, D. Corne, M. Dorigo, and F. Glover (eds.), McGraw-Hill, pp. 33–50, 1999.
T. Stützle and H. H. Hoos, “The MAX-MIN ant system,” Future Generation Computer Systems, vol. 16, pp. 889–914, 2000.
http://mscmga.ms.ic.ac.uk/jeb/orlib/wtinfo.html.
http://www.bwl.uni-kiel.de /Prod/psplib/index.html.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Merkle, D., Middendorf, M. Fast Ant Colony Optimization on Runtime Reconfigurable Processor Arrays. Genetic Programming and Evolvable Machines 3, 345–361 (2002). https://doi.org/10.1023/A:1020936909085
Issue Date:
DOI: https://doi.org/10.1023/A:1020936909085