Decentralized Dual-Based Algorithm for Computing Optimal Flows in a General Supply Chain

Abstract

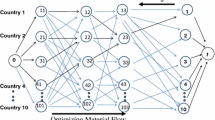
This paper addresses the issue of the optimal flow allocation in general supply chains. Our basic observation is that a distribution channel involving several reselling steps for a particular product can be viewed as a route in a supply chain network. The flow of goods or services along each route is influenced by the customer's demand, described by the corresponding utility functions, and prices charged at each node. We develop an optimization algorithm based on the primal-dual framework and the Newton's step that computes optimal prices at each node (dual problem) and then computes the optimal flow allocation (primal problem) based on these prices. Our main contribution is a discovery that the Newton's step leads to a partially decentralized algorithm which is a first step toward a decentralization schema for computing optimal prices.