Abstract
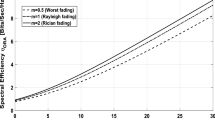
Order diversity combining technique is one of efficient methods to lower the complexity but not to significantly degrade performance. Recently, Eng and Milstein [1] proposed a novel order-combining technique, called the second order diversity combining (SC2) and third order diversity combining (SC3) and applied to Rayleigh fading channel. SC2 and SC3 schemes mean that the two (three) signals with the first two (three) largest amplitudes among the branches are chosen and coherently combined. However, when compared to Rayleigh distribution, the Nakagami-m distribution [10] provides a more general and versatile way to model wireless channel. For the reason, the bit error rate (BER) performance of proposed schemes were then analyzed with order statistic method and compared to the traditional diversity technique over Nakagami fading environment in this paper. The results are compared to maximal ratio combining (MRC), and conventional selection combining (SC) in coherent reception and to equal gain combining (EGC) in noncoherent reception. The results show that SC is in performance the worst for either in coherent or in noncoherent schemes, as expected. The performance differences between SC2 (SC3) and MRC (EGC) are not significant when the diversity order L ≤ 3, but the difference will increase when L ≥ 5. It is worth noting that the result of [1] is a special case with fading figure, m = 1. It is also observed the performance is much affected by the number of diversity branches L, the fading figure m, and the signal-to-noise ratio (SNR).
Similar content being viewed by others
References
T. Eng, N. Kong and L.B. Milstein, “Comparison of Diversity Combining Techniques for Rayleigh-fading Channels”, IEEE Trans. on Commun., Vol. 39, No. 9, pp. 1117–1129, 1996.
D.G. Brennan, “Linear Diversity Combining Technique”, Proceeding of the IRE, Vol. 47, pp. 1075–1102, 1959.
E.K. Al-Hussaini and Al-Bassiouni, “Performance of MRC Diversity Systems for the Detection of Signals with Nakagami Fading”, IEEE Trans. on Commun., Vol. 43, No. 12, pp. 1315–1319, 1985.
N. Kong and L.B. Milstein, “Combined Average SNR of a Generalized Diversity Combining Scheme”, in Proc. IEEE Int. Conf. Commun. ICC'98, Atlanta, GA, 1998, pp. 1556–1560.
V. Aalo and S. Pattaramalai, “Average Error Rate for Coherent MPSK Signals in Nakagami Fading Channels”, Electron. Lett., Vol. 32, pp. 1538–1539, 1996.
N.C. Beaulieu and A.A. Abu-Dayya, “Analysis of Equal Gain Diversity on Nakagami Fading Channels”, IEEE Trans. on Commun., Vol. 39, No. 2, pp. 225–234, 1991.
W.C. Jakes, Microwave Mobile Communications, John Wiley & Sons: New York, 1974.
J.G. Proakis, Digital Communications, McGraw-Hill: New York, 1995.
M. Schwartz, W.R. Bennett and S. Stein, Communication Systems and Techniques, McGraw-Hill: New York, 1966.
M. Nakagami, “The m-Distribution-A General Formula of Intensity Distribution of Rapid Fading”, in Statistical Methods in Radio Wave Propagation, Pergamon: Oxford, U.K., pp. 3–36, 1960.
H.A. David, Order Statistics, John Wiley & Sons, Inc.: New York, 1981.
S.S. Gupta, “Order Statistics from the Gamma Distribution”, Technometrics, Vol. 2, pp. 243–262, 1960.
I. Gradshteyn and I. Ryzhik, Tables of Integrals, Series, and Products, Academic: New York, 1994.
A. Annamalai and C. Tellamura, “Error Rate for Hybrid SC/MRC Systems on Nakagami-m Channels”, Wireless Communications and Networking Conference, 2000, WCNC, IEEE, Vol. 1, pp. 227–231, 2000.
Y. Ma and C.C. Chai, “Unified Error Probability Analysis for Generalized Selection Combining in Nakagami Fading Channels”, IEEE J-SAC, Vol. 18, No. 11, pp. 2198–2210, 2000.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Yang, Y., Chen, J.IZ. & Liu, JC. Ordered Statistic Analysis for Diversity Combining Schemes over Nakagami-m Fading Channel. Wireless Personal Communications 24, 463–481 (2003). https://doi.org/10.1023/A:1023223625766
Issue Date:
DOI: https://doi.org/10.1023/A:1023223625766