Abstract
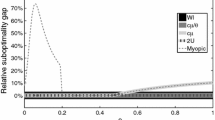
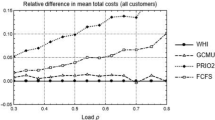
We consider the optimal service control of a multiclass M/G/1 queueing system in which customers are served nonpreemptively and the system cost rate is additive across classes and increasing convex in the numbers present in each class. Following Whittle's approach to a class of restless bandit problems, we develop a Langrangian relaxation of the service control problem which serves to motivate the development of a class of index heuristics. The index for a particular customer class is characterised as a fair charge for service of that class. The paper develops these indices and reports an extensive numerical investigation which exhibits strong performance of the index heuristics for both discounted and average costs.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
E. Altman and P. Nain, Optimal control of the M/G/1 queue with repeated vacations of the server, IEEE Trans. Automat. Control 38 (1993) 1766–1775.
P.S. Ansell, K.D. Glazebrook, I. Mitrani and J. Niño Mora, A semidefinite programming approach to the optimal control of a single server queueing system with imposed second moment constraints, J. Oper. Res. Soc. 50 (1999) 765–773.
P.S. Ansell, K.D. Glazebrook, J. Niño Mora and M. O'Keeffe, Whittle's index policy for a multiclass queueing system with convex holding costs, Math. Methods Oper. Res. (to appear).
D. Bertsimas and J. Niño Mora, Conservation laws, extended polymatroids and multi-armed bandit problems: A polyhedral approach to indexable systems, Math. Oper. Res. 21 (1996) 257–306.
A. Cobham, Priority assignment in waiting line problems, Oper. Res. 2 (1954) 70–76.
D.R. Cox and W.L. Smith, Queues (Methuen, London, 1961).
A. Federgruen and K.C. So, Optimality of threshold policies in single-server queueing systems with server vacations, Adv. in Appl. Probab. 23 (1991) 288–405.
J.C. Gittins, Multi-Armed Bandit Allocation Indices (Wiley, New York, 1989).
J.M. Harrison, Dynamic scheduling of a multiclass queue: discount optimality,Oper. Res. 23 (1975) 270–282.
G.P. Klimov, Time sharing systems I, Theory Probab. Appl. 19 (1974) 532–551.
J. Niño Mora, Countable partial conservation laws, Whittle's restless bandit index and a dynamic cµ rule for scheduling a multiclass M/M/1 queue with convex holding costs, Technical Report, Universitat Pompeu Fabra (2001).
M.L. Puterman, Markov Decision Processes: Discrete Stochastic Dynamic Programming (Wiley, New York, 1994).
R. Righter and S.H. Xu, Scheduling jobs on nonindentical IFR processors to minimize general cost functions, Adv. in Appl. Probab. 23 (1991) 909–924.
J.A. van Meighem, Dynamic scheduling with convex delay costs: The generalized cµ-rule, Ann. Appl. Probab. 5 (1995) 809–833.
R.R. Weber, Stochastic scheduling on parallel processors and minimization of concave functions of completion times, in: Stochastic Differential Systems, Stochastic Control Theory and Applications, Vol. 10 (Springer, Berlin, 1988) pp. 601–609.
G. Weiss, Branching bandit processes, Probab. Engrg. Inform. Sci. 2 (1988) 269–278.
P. Whittle, Restless bandits: activity allocation in a changing world, J. Appl. Probab. A 25 (1988) 287–298.
P. Whittle, Optimal Control: Basics and Beyond (Wiley, Chichester, 1996).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Glazebrook, K., Lumley, R. & Ansell, P. Index Heuristics for Multiclass M/G/1 Systems with Nonpreemptive Service and Convex Holding Costs. Queueing Systems 45, 81–111 (2003). https://doi.org/10.1023/A:1026060405346
Issue Date:
DOI: https://doi.org/10.1023/A:1026060405346