Skip to main content
SpringerLink
Log in

The Complexity of Symmetry-Breaking Formulas

  • Published:
Annals of Mathematics and Artificial Intelligence Aims and scope Submit manuscript

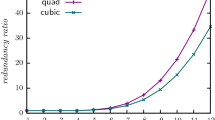
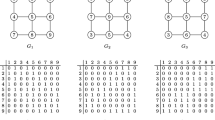
Abstract

Symmetry-breaking formulas for a constraint-satisfaction problem are satisfied by exactly one member (e.g., the lexicographic leader) from each set of “symmetrical points” in the search space. Thus, the incorporation of such formulas can accelerate the search for a solution without sacrificing satisfiability. We study the computational complexity of generating lex-leader formulas. We show, even for abelian symmetry groups, that the number of essential clauses in the “natural” lex-leader formula could be exponential. Furthermore, we show the intractability (NP-hardness) of finding any expression of lex-leadership without reordering the variables, even for elementary abelian groups with orbits of size 3. Nevertheless, using techniques of computational group theory, we describe a reordering relative to which we construct small lex-leader formulas for abelian groups.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. F.A. Aloul, I.L.Markov and K.A. Sakallah, Efficient symmetry breaking for boolean satisfiability, in: Proc. of Intl. Joint Conf. on Artificial Intelligence (IJCAI) (2003).

  2. L. Babai and E.M. Luks, Canonical labeling of graphs, in: Proc. of 15th ACM Symp. on Theory of Computing (1983) pp. 171–183.

  3. R. Backofen and S. Wilf, Excluding symmetries in constraint-based search, in: Proc. of 5th International Conference on Principle and Practice of Constraint Programming (CP'99), Lecture Notes in Computer Science, Vol. 1713 (Springer, 1999) pp. 73–87.

  4. B. Benhamou, Study of symmetry in constraint satisfaction problems, in: Principles and Practice of Constraint Programming (PPCP-94) (1994).

  5. C.A. Brown, L. Finkelstein and P.W. Purdom, Backtrack searching in the presence of symmetry, in: Applied Algebra, Algebraic Algorithms and Error Correcting Codes, 6th International Conference, ed. T. Mora (Springer, 1988) pp. 99–110.

  6. J. Crawford, A theoretical analysis of reasoning by symmetry in first-order logic (extended abstract), in: Workshop Notes, AAAI-92 Workshop on Tractable Reasoning (1992) pp. 17–22.

  7. J. Crawford, M. Ginsberg, E.M. Luks and A. Roy, Symmetry breaking predicates for search problems, in: Proceedings of the 5th International Conference on Knowledge Representation and Reasoning (KR'96) (1996) pp. 148–159.

  8. J.D. Dixon and B. Mortimer, Permutation Groups (Springer, New York, 1996).

    Google Scholar 

  9. K. Engel, Sperner Theory, Encyclopedia of Mathematics and Its Applications, Vol. 65 (Cambridge University Press, 1997).

  10. M.R. Garey and D.S. Johnson, Computers and Intractability: A Guide to the Theory of NPCompleteness (W.H. Freeman, New York, 1979).

    Google Scholar 

  11. J. Gathen and J. Gerhard, Modern Computer Algebra (Cambridge University Press, 1999).

  12. T. Grüner, R. Laue and M. Meringer, Algorithms for group actions applied to graph generation, in: DIMACS Series on Discrete Mathematics and Theoretical Computer Science, Vol. 28 (1997) pp. 113–122.

    Google Scholar 

  13. M. Hall, The Theory of Groups, 2nd ed. (Chelsea Publishing Company, New York, 1976).

    Google Scholar 

  14. D. Joslin and A. Roy, Exploiting symmetries in lifted CSPs, in: Proceedings of the Fourteenth National Conference on Artificial Intelligence, American Association for Artificial Intelligence (AAAI) (1997) pp. 197–203.

  15. G. Katona and J. Srivastava, Minimal 2-coverings of a finite affine space based on GF(2), J. Statist. Plann. Inference 8(3) (1983) 375–388.

    Google Scholar 

  16. J. Köbler, U. Schöning and J. Torán, The Graph Isomorphism Problem: Its Structural Complexity (Birkhäuser, Boston, MA, 1993).

    Google Scholar 

  17. C.W.H. Lam, L.H. Thiel and S. Swiercz, The non-existence of finite projective planes of order 10, Canadian Journal of Math XLI (1989) 1117–1123.

  18. S. Lang, Algebra (Addison-Wesley, Reading, MA, 1999).

    Google Scholar 

  19. E.M. Luks, Permutation groups and polynomial-time computation, in: Groups and Computation, Workshop on Groups and Computation, eds. W.M. Kantor and L. Finkelstein, DIMACS Series on Discrete Mathematics and Theoretical Computer Science, Vol. 11 (1993) pp. 139–175.

  20. E.M. Luks and A. Roy, in preparation.

  21. D. Miklós, Linear binary codes with intersection properties, Discrete Appl. Math. 9(2) (1984) 187–196.

    Google Scholar 

  22. J. Savage, Models of Computation, Exploring the Power of Computing (Addison-Wesley, Reading, MA, 1998).

    Google Scholar 

  23. H.N. Shapiro, Introduction to the Theory of Numbers (Wiley-Interscience, New York, 1983).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, University of Oregon, Eugene, OR, 97403, USA

    Eugene M. Luks

  2. Department of Computer Science, Boston College, Chestnut Hill, MA, 02167, USA

    Amitabha Roy

Authors
  1. Eugene M. Luks
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amitabha Roy
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Luks, E.M., Roy, A. The Complexity of Symmetry-Breaking Formulas. Annals of Mathematics and Artificial Intelligence 41, 19–45 (2004). https://doi.org/10.1023/B:AMAI.0000018578.92398.10

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/B:AMAI.0000018578.92398.10

Search

Navigation