Abstract
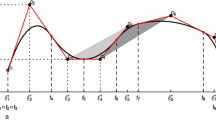
We consider n noisy measurements of a smooth (unknown) function, which suggest that the graph of the function consists of one convex and one concave section. Due to the noise the sequence of the second divided differences of the data exhibits more sign changes than those expected in the second derivative of the underlying function. We address the problem of smoothing the data so as to minimize the sum of squares of residuals subject to the condition that the sequence of successive second divided differences of the smoothed values changes sign at most once. It is a nonlinear problem, since the position of the sign change is also an unknown of the optimization process. We state a characterization theorem, which shows that the smoothed values can be derived by at most 2n − 2 quadratic programming calculations to subranges of data. Then, we develop an algorithm that solves the problem in about O(n 2) computer operations by employing several techniques, including B-splines, the use of active sets, quadratic programming and updating methods. A Fortran program has been written and some of its numerical results are presented. Applications of the smoothing technique may be found in scientific, economic and engineering calculations, when a potential shape for the underlying function is an S-curve. Generally, the smoothing calculation may arise from processes that show initially increasing and then decreasing rates of change.
Similar content being viewed by others
References
S.C. Bhargava, “A generalized form of the Fisher-Pry model of technological substitution,” Technological Forecasting and Social Change, vol. 49, pp. 27–33, 1995.
M.P. Cullinan, “Data smoothing using non-negative divided differences,” IMA J. Numer. Anal., vol. 10, pp. 583–608, 1990.
E.W. Cheney and W.A. Light, A Course on Approximation Theory, Book News Inc.: Portland, Or, 2000.
H. Chernof and L.E. Moses, Elementary Decision Theory. Dover Pub., Inc.: NY, 1986.
I.C. Demetriou, “Algorithm 742: L2CXFT: A Fortran 77 subroutine for least squares data fitting with non-negative divided differences,” ACM Trans. Math. Software, vol. 21, pp. 98–110, 1995.
I.C. Demetriou, “Signs of divided differences yield least squares data fitting with constrained monotonicity or convexity,” J. of Computational and Applied Mathematics, vol. 146, pp. 179–211, 2002.
I.C. Demetriou, “L2CXCV: A Fortran 77 package for least squares convex-concave data fitting,” Report Department of Economics, University of Athens, Greece, 2004.
I.C. Demetriou and M.J.D. Powell, “The minimum sum of squares change to univariate data that gives convexity,” IMA J. Numer. Anal., vol. 11, pp. 433–448, 1991.
I.C. Demetriou and M.J.D. Powell, “Least squares fitting to univariate data subject to restrictions on the signs of the second differences,” in Approximation Theory and Optimization, Tributes to M.J.D. Powell, M.D. Buhmann and A. Iserles (Eds.), Cambridge University Press, Cambridge, UK, 1997, pp. 109–132.
P. Dierckx, Curve and Surface Fitting with Splines, Clarendon Press: Oxford, UK, 1995.
W.J. Fabrycky, G.J. Thuesen, and D. Verna, Economic Decision Analysis, 3rd edition. Prentice Hall: New Jersey, 1998.
J.C. Fisher and R.H. Pry, “A simple substitution model of technological change,” Technological Forecasting and Social Change, vol. 3, pp. 75–78, 1971.
R. Fletcher, Practical Methods of Optimization, J. Wiley & Sons: Chichester, UK, 1987.
F.R. Giordano, M.D. Weir, and W.P. Fox, A First Course in Mathematical Modeling, 2nd edition. Brooks/Cole Pub. Co., London, UK, 1997.
D. Goldfarb and G. Idnani, “A numerically stable dual method for solving strictly convex quadratic programs,” Math. Programming, vol. 27, pp. 1–33, 1983.
R.C. Gonzalez and P. Wintz, Digital Image Processing, 2nd edition. Addison-Wesley Pub. Co.: Mass., 1987.
D.L. Hanson and G. Pledger, “Consistency in concave regression,” Annals of Stat., vol. 4, pp. 1038–1050, 1976.
W. Hock and K. Schittkowski, Test Examples for Nonlinear Programming Codes, Lecture Notes in Economics and Mathematical Systems, no. 187, Springer-Verlag: Berlin, Germany, 1981.
V. Kafarov, Cybernetic Methods in Chemistry and Chemical Engineering, English Translation, MIR Publishers, Moscow, 1976.
W. Li, D. Naik, and J. Swetits, “A data smoothing technique for piecewise convex/concave curves,” SIAM J. Sci. Comput., vol. 17, no. 2, pp. 517–537, 1996.
D.V. Lindley, Making Decisions, 2nd edition, J. Wiley and Sons: London, UK, 1985.
T. Modis, “Technological substitutions in the computer industry,” Technological Forecasting and Social Change, vol. 43, pp. 157–167, 1993.
T. Modis, Conquering Uncertainty, McGraw-Hill, Inc.: NY, 1998.
J. Nocedal and S.J. Wright, Numerical Optimization, Springer Series in Operations Research, N.Y., 1999.
M.E. Porter, Competitive Advantage. Creating and Sustaining Superior Performance, The Free Press, a Division of Macmillan, Inc.: NY, 1985.
M.J.D. Powell, Approximation Theory and Methods, Cambridge University Press: Cambridge, UK, 1981.
M.J.D. Powell, “On the quadratic programming algorithm of Goldfarb and Idnani,” Math. Programming Studies, vol. 25, pp. 46–61, 1985.
H. Raiffa, Introductory Lectures on Choices under Uncertainty, Addison-Wesley Pub. Co.: Mass, 1970.
B. Rustem and M. Howe, Algorithms for Worst-Case Design and Applications to Risk Management, Princeton University Press: Princeton and Oxford, 2002.
J. von Neumann and O. Morgenstern, Theory of Games and Economic Behavior, 2nd edition, Princeton University Press: Princeton, 1947.
von Winterfeldt and W. Edwards, Decision Analysis and Behavioral Research, Cambridge University Press: Cambridge, UK, 1986.
S.R. Watson and D.M. Buede, Decision Synthesis, The Principles and Practices of Decision Analysis, Cambridge University Press: Cambridge, UK.
J.B. West, Respiratory Physiology—the Essentials, 3rd edition, Williams & Wilkins: Baltimore, 1985.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Demetriou, I. Least Squares Convex-Concave Data Smoothing. Computational Optimization and Applications 29, 197–217 (2004). https://doi.org/10.1023/B:COAP.0000042030.54793.47
Issue Date:
DOI: https://doi.org/10.1023/B:COAP.0000042030.54793.47