Abstract
The spatiotemporal organization of membrane-associated molecules is central to the regulation of cellular signals. Powerful new microscopy techniques enable the 3D visualization of localization and activation of these molecules. However, the quantitative interpretation and comparison of molecular organization on the 3D cell surface remains challenging because cells themselves vary greatly in morphology. Here, we introduce u-signal3D, a framework to assess the spatial scales of molecular organization at the cell surface in a cell-morphology invariant manner. We validated the framework by analyzing synthetic signaling patterns painted onto observed cell morphologies, as well as measured distributions of cytoskeletal and signaling molecules. To demonstrate the framework’s versatility, we further compared the spatial organization of cell surface signals both within and between cell populations and powered an upstream machine-learning based analysis of signaling motifs.
Many cell functions depend on the subcellular regulation of signal transduction. Cells regulate signaling patterns through nonlinear circuitry of activators and inhibitors and by directly controlling the localization of molecular components1,2. Confinement on membranes, in scaffolds, or via phase separation, all serve to localize reactions3. Accordingly, molecular activities vary across space and time, requiring live cell microscopy and appropriate image analytics for quantifying cell signaling.
One of the most important organizers of molecular signals is the plasma membrane itself4. The plasma membrane acts as both a platform and a conduit for the chemical reactions that range from local nano- or microscale puncta to global bursts that span the entire cell (Fig. 1A)5,6. Deciphering the regulatory principles that define these scales requires a comprehensive quantification of molecular concentration and activity at the 3D cell membrane. This task is complicated by the fact that cells configure their plasma membranes into a wide range of 3D morphologies7. Signaling data, such as those probed by a fluorescence biosensor of protein activity, can be projected onto the 3D cell surface to facilitate analysis (Fig. 1B)7–9. However, this alone does not enable quantitative comparisons of signaling organization. A natural ordering or parameterization of the surface signal is required that is consistent across variable morphologies.
Fig. 1. Spatial organization of molecular distributions on the 3D cell surface.
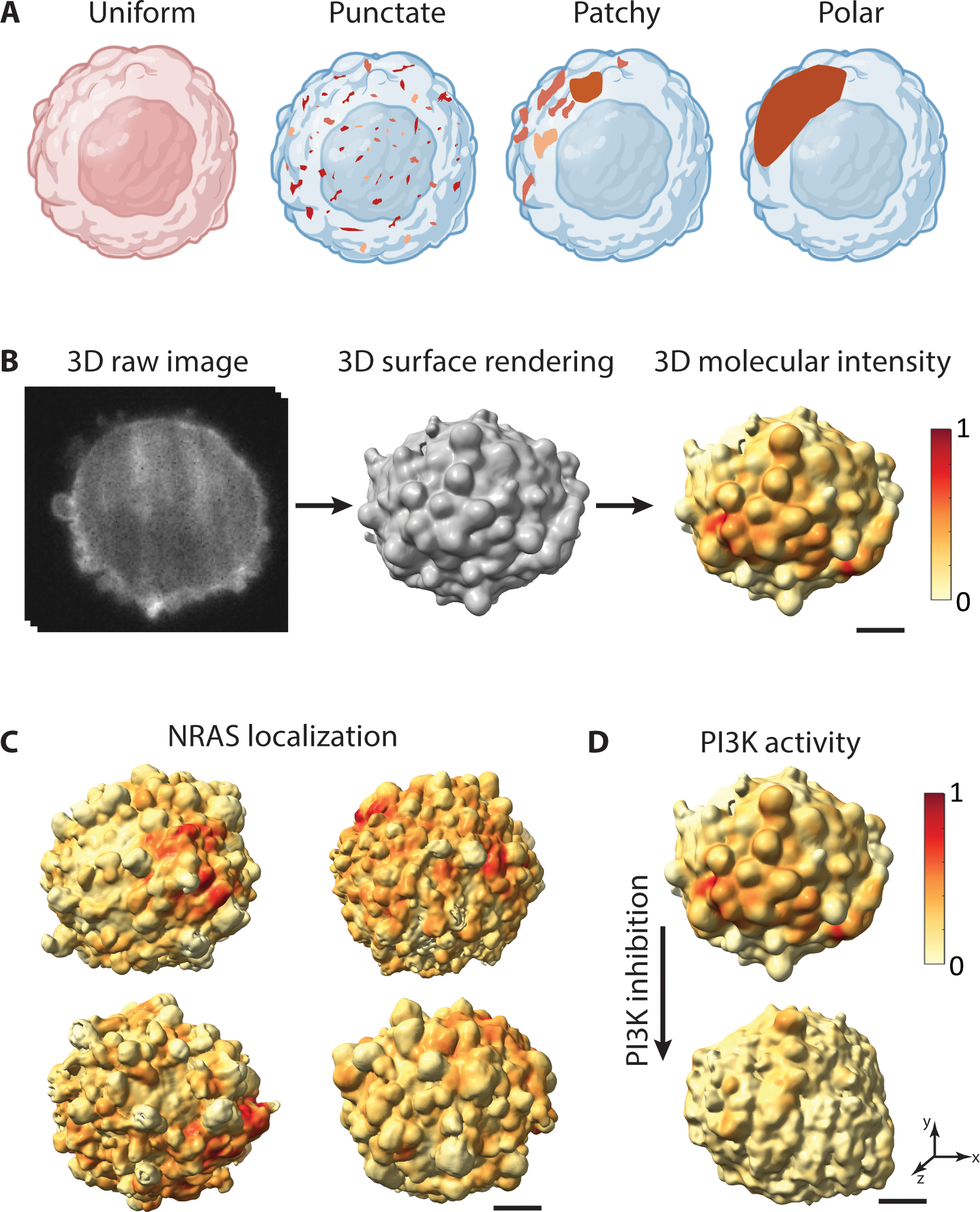
A. Membrane-associated proteins (brown) can spatially organize across scales ranging from a uniform distribution or punctate clustering to a highly polarized configuration. B. 3D raw image of an MV3 melanoma cell with PI3K activity labeled using a fluorescent biosensor (GFP-AktPH) (left), surface rendering of the same cell (middle) with localization of PI3K activity projected onto the 3D cell surface (right). Red surface regions indicate high local PI3K activity. C. NRAS-GFP localization projected onto the 3D cell surface of MV3 melanoma cells. D. PI3K activity projected onto an MV3 melanoma cell before (top) and after (bottom) treatment with a PI3K inhibitor. Scale bars: 2 μm.
To normalize surface signal distributions, 3D analysis frameworks have considered a combination of geometry and molecular organization10, constrained cell shape by micro-patterned surfaces11, or normalized the cell shape based on global cell shape features12–14. Tools to normalize and analyze molecular distributions in cells adopting unconstrained morphologies are missing.
We propose a spectral approach, in which the surface distribution is broken down into a set of elementary modes that spans a wide range of spatial scales. A natural candidate for spectral decomposition of data on the cell surface is the Laplace-Beltrami operator (LBO), which constructs a mathematically complete set of Fourier-like modes on surfaces15,16. These modes are invariant to isometric transformations17 and are independent of shape representation, parametrization and spatial position. These properties have been leveraged in computer science to quantify the global characteristics of 3D shape17,18, and the LBO has been modified to represent local morphological motifs19–22. Because of its ubiquitous use in the computer graphics field, the efficiency and stability of LBO implementations have been extensively characterized23–25. In the biomedical sciences, the LBO has been used to describe brain images26–30, and spherical harmonics, which are the LBO modes of a sphere, to represent 3D cell shapes31–33. Here, we exploit the LBO to establish a spectral representation of the cell surface signal variation that is agnostic to the underlying cell shape variation. Specifically, we introduce u-signal3D, a cellular manifold harmonics pipeline to i) compare the spatial organization of signaling over time (Supplementary Video 1) or across cell populations (Fig. 1C), ii) measure subcellular signaling responses to acute experimental intervention (Fig. 1D), iii) perform generative modeling of representative signaling distributions, and iv) classify features of signaling distributions across cells and conditions via machine learning.
Results
Pipeline overview.
The u-signal3D pipeline accepts 3D images or triangle meshes with associated signaling data as input and outputs spectra describing the spatial organization of surface signal distributions that can be compared across morphologies. For convenience, the pipeline includes the cell surface segmentation functionality of our previous software pipeline, u-shape3D, which generates surface meshes from 3D images34. To meet the numerical requirements for LBO applications, we modified u-shape3D’s mesh generating process to keep only a single mesh component (Supplementary Fig. 1A, see Methods). The u-signal3D pipeline incorporates two implementations of the LBO, one optimized for computational speed35,36, and one robust on non-manifold meshes24 (Supplementary Fig. 1B, see Methods).
The LBO computes the local geometrical variation of a 3D surface and defines a mathematically complete set of manifold harmonic functions, referred to as cellular harmonics, ordered by increasing frequency and conformed to the morphology (Fig. 2A). The cellular harmonics simultaneously encode the spatial scale and orientation relative to the cell shape. For an irregularly shaped cell, the morphological complexity complicates intuitive interpretations of these harmonics. In the limit of a perfect sphere, the LBO yields the hierarchy of the spherical harmonics, with functions at low frequency levels capturing surface signal variations that span the entire sphere and functions at higher levels capturing increasingly finer-grained variations (Fig. 2B, see Methods). In general, the LBO yields manifold harmonics similar to spherical harmonics but conformed to the geometrical undulations of particular 3D morphologies. Thus, we arranged the LBO modes into a spherical harmonics style pyramid (Fig. 2C.i). Mathematically, the eigenvectors of the LBO form an orthogonal basis of RN, where N is the number of mesh vertices. Hence, the eigenvalues can be considered pseudo-frequencies of the geometry defined over the mesh graph and ordered inversely with the length scale of surface undulation (Fig. 2C.ii). Surface-associated molecular distributions can therefore be quantified by projection of the pattern onto the LBO eigenvectors.
Fig. 2. Cellular harmonics for the analysis of molecular distributions on the 3D cell surface.
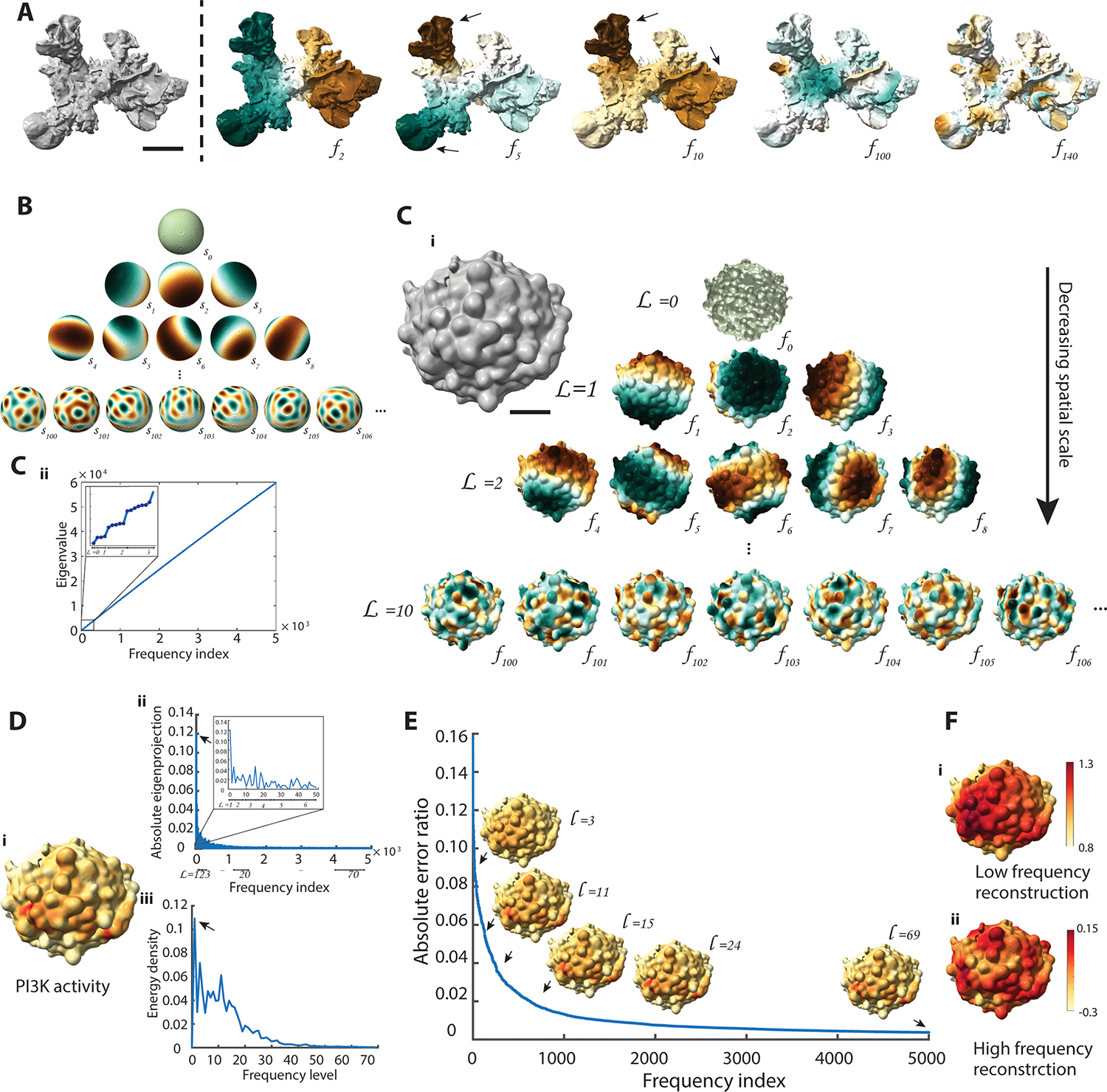
A. Surface rendering of a dendritic cell (left) and select modes of its cellular harmonic basis () (right). Brown and green colors represent positive and negative values, respectively. Black arrows indicate eigenvector magnitudes that follow protrusions in the underlying cell morphology. The cell surface was generated from the Lifeact-GFP-signal visualizing cortical actin filament structures (data not shown). Scale bar: 2 μm B. Select modes of spherical harmonic basis (), representing LBO eigenvectors applied to a sphere. The spherical harmonics naturally organize into a pyramid. C. Surface rendering of an MV3 melanoma cell expressing GFP-AktPH, a marker of PI3K activity. Scale bar: 2 μm. C.i. LBO eigenvectors () arranged hierarchically into a pyramid from low frequency level () to high frequency level. C.ii. LBO eigenvalues plotted as a function of LBO frequency index. Inset: zoomed-in region of the LBO eigenvalues plot showing only the first three frequency levels. D. Reconstruction of surface signal by cellular harmonics. D.i. PI3K activity projected onto the cell surface shown in (C). D.ii. Absolute value of the LBO eigenprojection profile over the cellular harmonics index. D.iii. Energy density spectra of PI3K activity over frequency levels. E. Absolute error ratio between the reconstructed data and the original signal as a function of the number of frequency indices in the reconstruction. Black arrows indicate 3D reconstructed data visualized up to levels, L=3, 11, 15, 24, and 69. F. Reconstructed PI3K activity from the LBO eigenvectors showing only low frequency (L=1 to L=20) or high frequency (L=20 to L=69) information. Color scale is adjusted for visualizing the high-frequency variations.
Characterizing molecular distributions on the cell surface.
We demonstrate the spectral representation of cellular signals by the LBO for a fluorescent reporter of PI3-Kinase (PI3K) activity on the surface of MV3 melanoma cell (Fig. 2Di). The contribution of each eigenvector to the total surface signal is visualized via the function pyramid of Fig. 2C.i weighted by the magnitude of the matching eigenprojection (Supplementary Fig. 2A). PI3K activity has previously been shown to follow a polarized distribution with increased signaling at the cell front37. Accordingly, the strongest eigenprojections associate with eigenvectors at level (black arrow, Fig. 2D.ii), whereas the projections for higher levels decrease near monotonically.
Distinct cell states are associated with distinct signaling patterns, encoded by contributions from different spatial scales. However, the pattern orientation, determined by the relative weights of the basis functions at one scale, can be ignored. Thus, to calculate an interpretable spectral signature for any given cell surface pattern, we separated spatial frequency from pseudo-orientation by integrating across the spherical harmonics levels.
The overall intensity of the fluorescence signal often varies between cells due to the concentration of the probes. To eliminate this factor, we first normalized the fluorescence intensity and further calculated an energy density across levels. This energy measures the signal gradient under Dirichlet boundary conditions, which is valid for a closed 3D shape (see Methods). The Dirichlet energy density provides a quantitative measure of how much each frequency level contributes to the organization of the surface signal. For the PI3K activity in Fig. 2D.i, the Dirichlet energy density reveals that the signal is organized across a range of higher spatial frequencies beyond the low-level frequencies that capture front-back polarization (black arrow, Fig. 2D.iii).
Given the parameterization of a surface signaling pattern by frequency levels, we can regenerate sub-patterns containing only particular spatial scales. For example, we reconstructed the PI3K activity using LBO eigenvectors up to and 69 (Fig. 2E). The absolute error ratio between reconstructed and original signal decreases with inclusion of higher levels (Fig. 2E, Supplementary Fig. 2B), confirming that LBO eigenvectors describe the signal completely given sufficient eigenvectors. This property can be leveraged for denoising the signaling patterns by suppression of high-frequency basis functions (Supplementary Fig. 2C). Moreover, we were able to separate low frequency from high frequency components, with the former representing the signaling pattern at the cell scale, and the latter the spatial distribution of localized signaling hotspots (Fig. 2F).
Validation of spectral decomposition on the cell surface.
To validate the decomposition of cell surface signals across spatial scales, we generated synthetic patterns on both experimental and modeled cell geometries. The frequency-dependent behavior of optical instruments is commonly assessed via stripe patterns, such as Ronchi rulings38. Stripe patterns cannot be applied to the highly curved surfaces of cells with any consistency. We instead introduced polka dots consisting of circular shapes of equal radius arranged as far apart as possible on the cell surface (Supplementary Fig. 3A, see Methods). Generating variously scaled polka dot patterns allowed us to simulate surface signal distributions ranging from front-back polarization to punctate micro-clusters (Fig. 3A). Applied to a sphere, coarse- to fine-grained polka dot patterns yielded spectral peaks at increasingly higher frequency levels (Fig. 3A). For each pattern, secondary lower peaks occur due to sharp boundaries at the polka dot edge. They vanish upon smoothing the polka dot pattern (Supplementary Fig. 3B). The primary peaks across various patterns broaden at higher frequencies. Although the spherical harmonics have the same spatial angular frequency at each pyramid level, the number of peaks varies (Supplementary Fig. 4A). At higher frequency levels, similar peak numbers are shared by a greater range of levels (Supplementary Fig. 4B). Consequently, polka dot number and angular spatial frequency are not perfect analogues, even though both capture spatial scale information. Additionally, changing the dot radius changes the energy spectra peak magnitude without changing its corresponding frequency level (Fig. 3B, Supplementary Fig. 3C), demonstrating that the relative distance and number of dots determine the spatial scale of a pattern, and not the dot radius.
Fig. 3. Validation and robustness of spectral decomposition analysis.
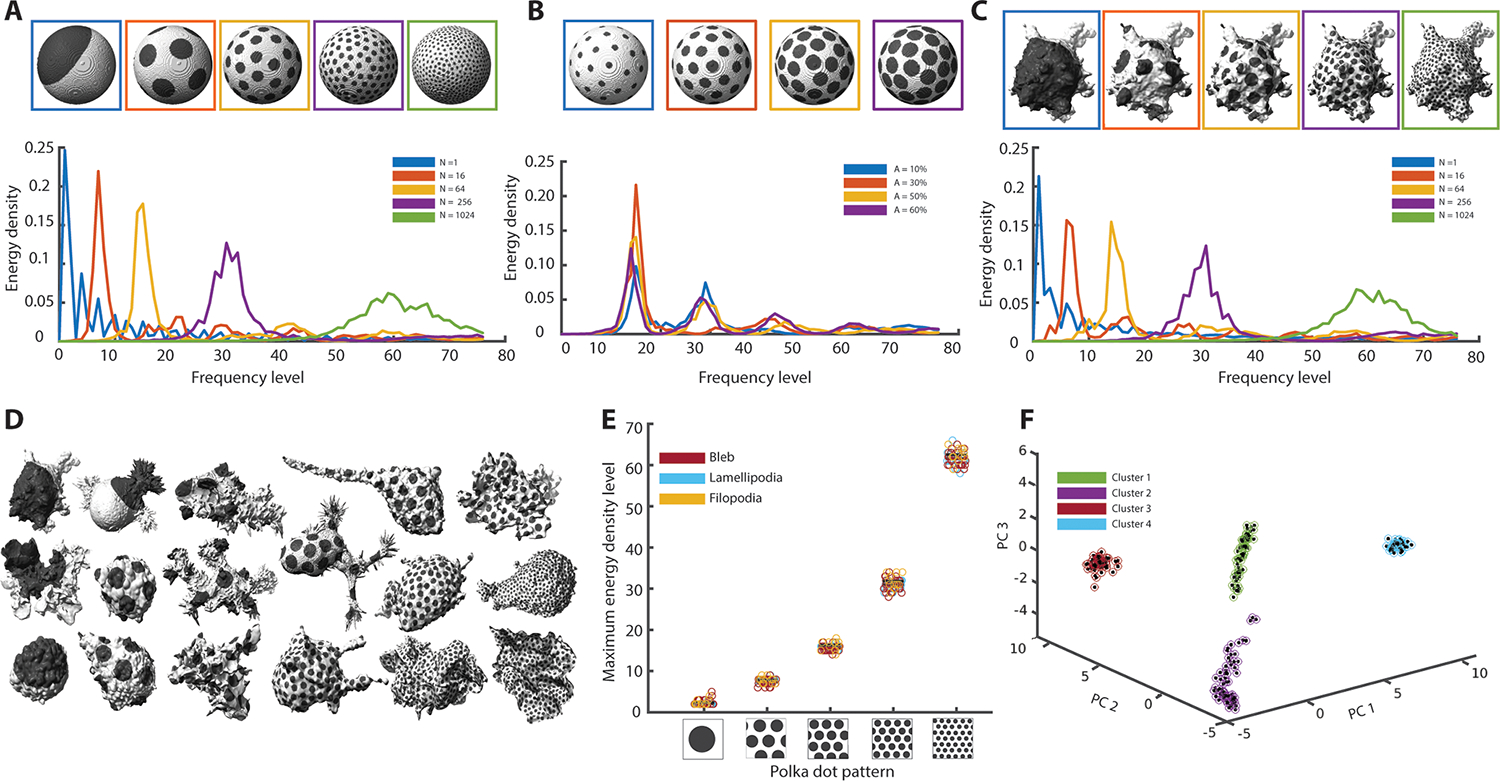
A. Polka dot patterns on a sphere with increasing numbers of dots, from left to right N = 1, 16, 64, 256, and 1024 (top). Corresponding energy density spectra (bottom). B. Polka dot patterns on a sphere with 64 dots painting 10%, 30%, 50% and 60% of the total surface area (top). Corresponding energy density spectra (bottom). C. Polka dot patterns as in (A) applied to the 3D cell surface of an MV3 melanoma cell expressing tractin-GFP (top). Corresponding energy density spectra (bottom). D. Polka dot patterns on a variety of MV3 melanoma cells, dendritic cells and human bronchial epithelial cells (HBECs). Numbers of dots number increase from left to right N = 1, 16, 64, 256, and 1024. E. Scatter plot of the energy density peak for 67 MV3 (morphological motif is blebs), dendritic (morphological motif is lamellipodia), and HBEC (morphological motif is filopodia) cells painted with polka dot patterns of N = 1, 16, 64, 256, and 1024 dots. F. Principal component analysis of energy density spectra for the cells in (E) with polka dot patterns of N = 16, 64, 256, and 1024 dots. Colored circles are clusters determined via the k-means algorithm.
Analyzing the same polka dot patterns on a melanoma cell surface, we recovered spectra similar to the patterns on the sphere (Fig. 3C). Hence, the spectral decomposition is largely independent of the underlying surface morphology. To more formally test the consistency of spectra across cell morphologies, we first applied a polka dot pattern to a sphere and similarly sized ellipsoids (Supplementary Fig. 3D). Regardless of shape eccentricity, the spectra coincided. We then applied five different patterns to a cell library with lamellipodia (thin, sheet-like membrane protrusions), blebs (hemispherical membrane protrusions), or filopodia (elongated and spiky membrane protrusions) (Fig. 3D, Supplementary Fig. 5)34. We found consistent spectral peaks over 67 different cell morphologies (Fig. 3E). Our spectral decomposition thus characterizes the spatial scales of cell surface patterns in a cell shape-agnostic manner.
To validate the conclusions from these synthetic data in more general scenarios, we first painted only a portion of the cell surface with polka dots to break the uniformity (Supplementary Fig. 6A). The energy spectra peak at the frequency level of the uniform pattern, but the asymmetry of surface coverage generates a second, weaker, low frequency peak. We also confirmed that our framework could properly detect the superposition of two patterns with distinct dot numbers (Supplementary Fig. 6B). Next, we distributed the polka dots randomly (Supplementary Fig. 6C). Compared to the energy spectra of uniform patterns, the corresponding non-uniform patterns generated spectra with similar dominant frequency levels but wider peaks. Hence, the peak frequency reflects the average distance between polka dots, even when individual neighbor-to-neighbor distances vary across the cell. Finally, we tested the sensitivity of energy spectra to noise (Supplementary Fig. 7). We employed two methods to disturb a given baseline polka dot pattern: i) we changed the intensity value of every surface mesh node by adding a random value from a uniform distribution (intensity noise); ii) we spatially blurred the pattern by translocating the value of a surface mesh node to another node in a predefined neighborhood (spatial shuffling). The energy spectrum of a surface signal with random intensity values in every mesh node increases monotonically across the frequency levels (Supplementary Fig. 7A), indicating the implicit low-pass filtering properties of the LBO. We added increasing intensity noise to a polka dot pattern until the dominant pattern vanished (see Methods). Low level noise marginally altered the measured spectra of polka dot patterns or molecular distributions. However, when the range of noise began to equal that of the signal, regardless of the dot size, the effects of the noise dominated the spectra, particularly at high frequency levels (Supplementary Fig. 7B, C, D, E). The peaks of the energy spectra are remarkably resistant to spatial shuffling, in line with our previous conclusion that the spectrum maxima capture the mean distance between the dots (Supplementary Fig. 7F). Only when the shuffling neighborhoods become similar and greater than the dot size do the energy spectra raise at high-frequency levels outside the frequency band of the underlying pattern. Finally, we tested the sensitivity of the spectra to reduction in mesh density while maintaining the cell shape (Supplementary Fig. 8A). The energy spectra remain remarkably similar even with a 100-fold reduction in surface mesh nodes, although the maximum frequency level is limited to the number of vertices.
Measuring cellular harmonics further allows us to parameterize surface signals for downstream analyses such as machine learning applications. In Fig. 3F we show the application of principal component analysis to reduce the dimensionality of the energy density spectra on 67 cell morphologies of the four polka dot patterns introduced in Fig. 3D, E. Independent of the cell morphology, each polka dot pattern appears as a distinct cluster in the reduced space of the first three principal components. Performing a similar cluster analysis directly on the intensities projected onto the cell surface is impossible, because there is no natural ordering of intensities that is consistent between cells with highly diverse morphologies.
In summary, our validation based on polka dots established the ability of the pipeline to measure the spatial organization of cell surface patterns independent of the underlying cell shape.
Spectral analysis of molecular patterns on cell surfaces.
To illustrate the utility of cellular harmonics in biological experiments, we analyzed molecular distributions on melanoma cells imaged in 3D culture by high-resolution light-sheet microscopy37,39,40. First, we compared the cell surface distributions of two co-imaged molecular signals. Melanoma cells in soft collagen tend to extend dynamic blebs39. Expanding blebs are thought to be largely devoid of cortical actin whereas retracting blebs have increased cortical actin41. Thus, a snapshot of cortical filamentous actin at a single time-point of a blebbing cell is expected to display a patchy fluorescent signal over the entire cell surface (Fig. 4A.i and Supplementary Video 2). We measured the localization of filamentous actin (CyOFP-tractin) and a cytosolic GFP marker within a 1 μm sampling radius of the cell surface. Averaged across five cells, filamentous actin shows peaks in spatial organization at mid-range energy levels with the maximum at L = 13 and a full width at half maximum (FWHM) of 15 levels (Fig. 4A.ii, Supplementary Fig. 8B). Surprisingly, the cytosolic marker also shows spatial organization across a range of energy levels with wider FWHM (20 levels), suggesting that its distribution is not homogenous. Indeed, the raw data (Supplementary Video 3) displays a spatial patterning, such as a reduction in intensity within blebs, probably because of the limited diffusion of GFP molecules into the narrow space of blebs. Of note, the first peak in both cytosol and tractin energy density spectra is associated with an illumination gradient across the entire cell, which is clearly recognizable in the maximum projection images (Fig. 4A.i).
Fig. 4. Decomposing the spatial organization of cell surface signaling on melanoma cells.
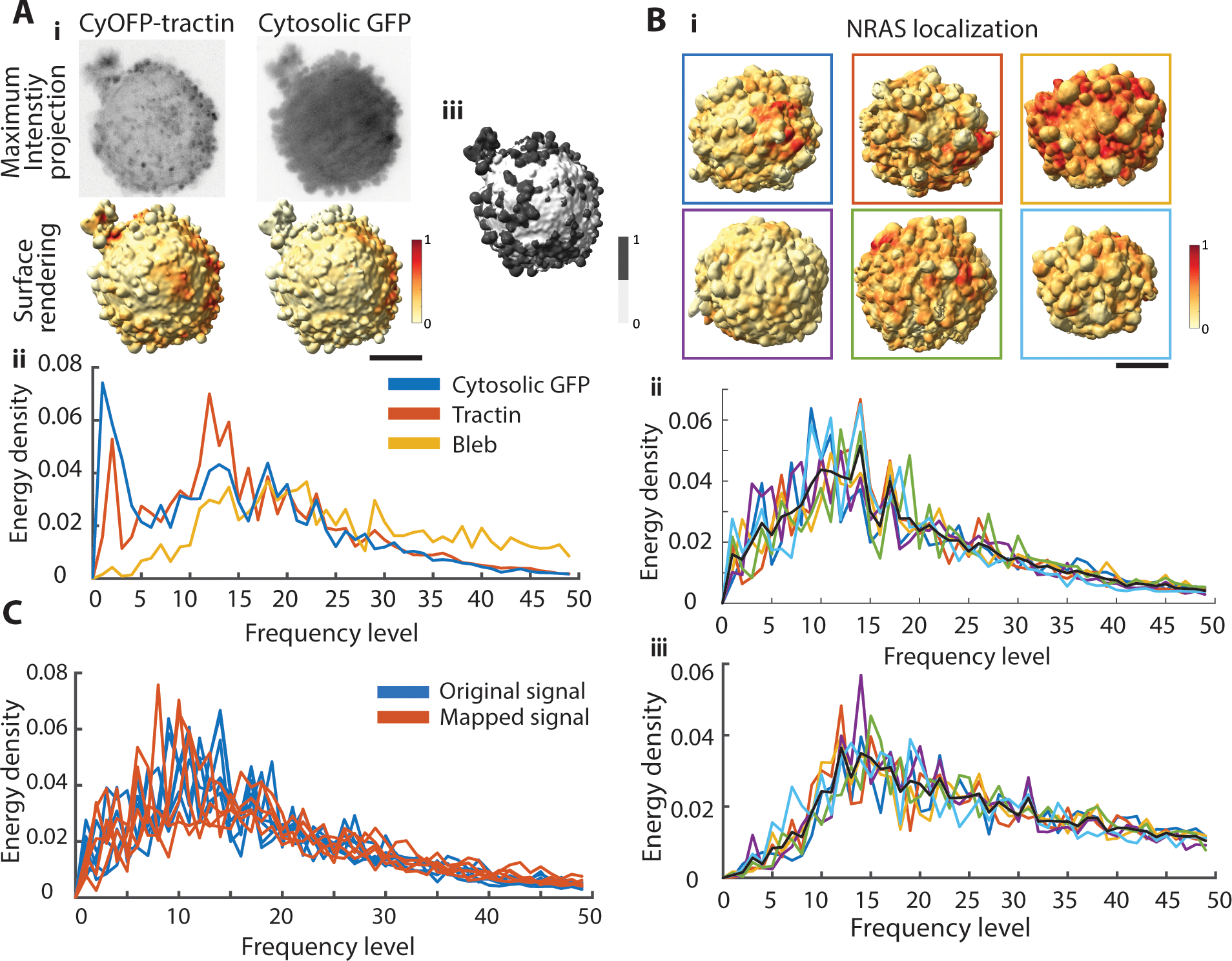
A.i. Maximum intensity projections of an MV3 melanoma cell labeled with an actin marker, CyOFP-tractin, and cytosolic GFP (top). Surface renderings of the same cell with fluorescence intensities projected onto the cell surface (bottom). Red indicates regions of high fluorescence intensity, yellow regions of low intensity. A.ii. Energy density spectra of a cytosolic marker (blue curve), CyOFP-tractin (red curve), and the binary on-/off-bleb distribution (yellow). A.iii. Segmentation of blebs (dark gray) vs non-bleb (white) was performed by u-shape3D software34. Scale bar: 2 μm. B.i. Surface renderings of MV3 melanoma cells expressing NRAS-GFP with fluorescence intensities projected onto the cell surfaces. Scale bar: 2 μm. Energy density spectra of NRAS localization (B.ii) and bleb distribution (B.iii). Line colors in correspondence with box colors in (B.i). The black curve in each panel is the average energy density spectra across six cells. C. Energy density spectra of NRAS localization of MV3 melanoma cells (n = 5) on the original mesh (blue) and mapped to a new mesh (red).
To enable interpretation of energy spectra, we calculated an approximate conversion between energy level and actual spatial scale. To do so, we measured the relative distances amongst polka dots distributed on 11 blebby cells (Supplementary Fig. 8C). Comparison between the spectra of CyOFP-tractin and polka dot patterns for MV3 cells suggests that filamentous actin is organized at a peak length scale of 7 μm for the energy peak at L =13 (Supplementary Fig. 8C). Moreover, these analyses indicated that 50 frequency levels are sufficient to represent energy density spectra at a spatial resolution above 1 μm, which is the limit imposed by the sampling radius of fluorescence intensity (dashed line in Supplementary Fig. 8C, see Methods). To test the possibility that the spatial pattern of actin filaments relates to the spatial pattern of blebs, we detected blebs using the u-shape3D software34 and converted the segmentation into a binary cell surface pattern (Fig. 4A.iii). The energy spectra of bleb distribution peaks (L= 16 with a FWHM of 17 levels) at a spatial scale of 5 μm (Supplementary Fig. 8C), i.e. at somewhat higher frequency ranges than the CyOFP-tractin signal. Hence, on a blebby cell filamentous actin density varies over longer distances than bleb formation, as one would expect for a snapshot, in which only the fraction of retracting blebs is filled with actin filaments.
Next, we analyzed the spatial organization of wild type NRAS signaling in melanoma cells (Fig. 4B). Across six cells, the NRAS organization peaked at mid-range energy levels (L=13 with a FWHM of 17 levels) corresponding to spatial scales of 7 μm (Supplementary Fig. 8D). NRAS is recruited to the membrane by bleb-related scaffold proteins39. Thus, we hypothesized that the spatial scale of NRAS signaling relates to the length scale of bleb-induced surface undulations. We detected blebs on the cell surface using the u-shape3D software34 (Supplementary Fig. 9). Compared to the bleb spectra, the NRAS spectra were somewhat skewed to lower frequency levels (Fig. 4Bii & iii, Supplementary Fig. 9). Thus, we concluded that while the bleb distribution in these melanoma lacks an axis of preferential organization, the NRAS distribution is at least in part determined by secondary, long-range mechanisms that structure organization at scales larger than that of blebs.
To check whether our framework could evaluate the spatial signature of a surface signal in a shape-invariant manner for an experimentally derived surface pattern, we transferred both a polka dot pattern and experimentally measured NRAS patterns from one cell to another cell using an orbifold Tutte embedding texture mapper42. The energy spectra of the original and mapped polka dot patterns and NRAS organization display similar spatial signatures on both cell surfaces (Supplementary Fig. 10A & 10B top row). For five cells the spatial scales were preserved regardless of cell morphology (Fig. 4C, Supplementary Fig. 10B).
To further validate our framework, we measured the spatial organization across a perturbation with expected effects on the organization of septin. Septin is a curvature sensitive molecule that associates to the base of blebs39. Bleb formation is inhibited by wheat-germ agglutinin (WGA)43. Thus, in untreated cells, septin is organized in patches near the base of blebs (Fig. 5Ai left), whereas the patches disappear under WGA treatment (Fig. 5Ai right), yielding a spectrum without a preferential scale. We measured the energy spectra of 10 untreated cells and seven WGA-treated cells (Fig. 5Aii). Per KS test on the average curves, the energy spectra are statistically distinct between the two conditions (p-value 0.016).
Fig. 5. Evaluating the spatial redistribution of cell surface signaling on melanoma cells.
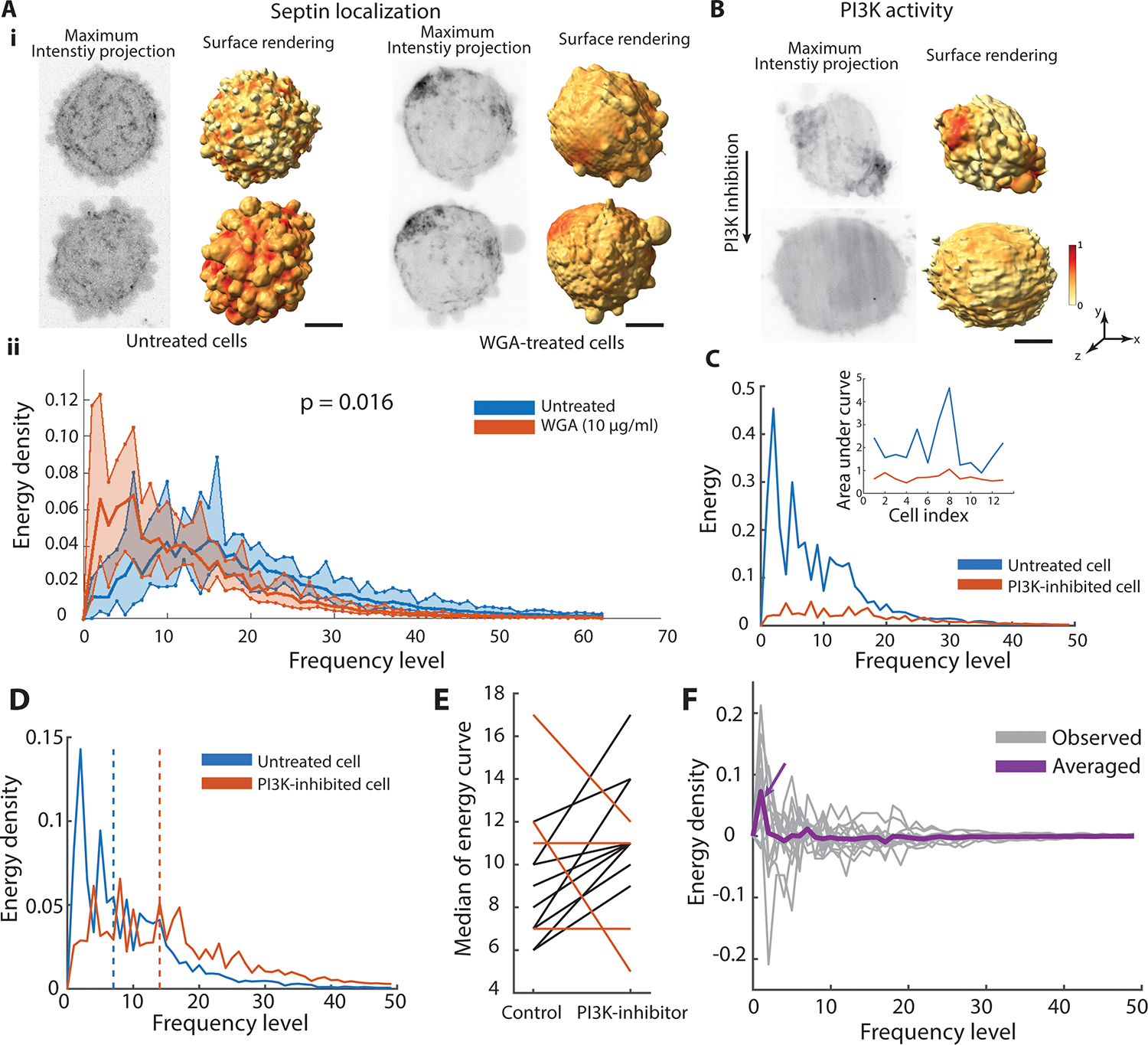
A.i. Maximum intensity projections and molecular surface projections of septin localization on untreated (left) and WGA-treated MV3 melanoma cells (right). A.ii. Energy spectra of septin organization in untreated cells (blue curve, n=10 cells) and WGA-treated cells (red curve, n=7 cells). Bold curves indicate the mean of the energy density per level for each condition. Shaded bands indicate the range from minimum to maximum of the energy density per level for each condition. P-value indicates two-sided Kolmogoroff-Smirnov test comparing the averaged energy curve in untreated and WGA-treated cells. B. Maximum intensity projections (left) and surface projections (right) of an MV3 melanoma cell, expressing GFP-AktPH, a marker of PI3K activity, before (top) and after (bottom) PI3K inhibition. C. Energy spectra of PI3K activity on the same cell before (blue) and after (red) PI3K inhibition. Inset: Area under the energy spectra curve of PI3K activity for 13 cells before (blue) and after (red) PI3K inhibition. D. Energy density spectra of PI3K activity before (blue) and after (red) PI3K inhibition. The dashed line indicates the median frequency level of the energy density spectra. E. Median energy density of PI3K activity between untreated and PI3K-inhibited cells (n=13 cells). Cells exhibiting a nonpositive shift after PI3K inhibition treatment, which deviates from the generally positive shifts, are indicated by red lines. F. The differences curve of energy spectra between untreated and PI3K-inhibited cells (gray curve is for a single cell, purple curve is averaged across 13 cells). Scale bar: 2 μm.
Polarized cell signaling is often accompanied by polarized cell morphology. Our framework allows the disentangling of morphology-driven from signaling-driven polarization. For example, PI3-Kinase activity is known to be polarized in migrating melanoma cells that themselves have polarized morphologies37. We measured PI3K activity via a fluorescent biosensor (GFP-AktPH) both before and after treatment with a PI3K inhibitor (PI3Kα Inhibitor). This biosensor reports PI3K activity by localizing to PI3K effector products PIP2 and PIP3. Even when the effects of a polarized morphology were excluded by applying cellular harmonics as the base functions, the high energy at low frequency levels indicated significant polarization of the PI3K activity. Upon PI3K inhibition, the overall energy spectra are reduced (Fig. 5B,C), indicating that the spatial organization of the PI3K signal is governed at least in part by the PI3K activation level. The area under the energy curve for 13 cells demonstrates the energy reduction after PI3K inhibition for individual cells (Fig. 5C inset). Moreover, even on a relative scale the energy density at low frequencies is suppressed, showing that PI3K inhibition abrogates polarity in signaling (Fig. 5D, Supplementary Video 4). Calculating the median frequency level of energy density spectra (dashed lines in Fig. 5D) before and after treatment, we found the trend of PI3K inhibition raising the frequency level of the energy density distribution (Fig. 5E). Among the 13 cells analyzed, 9 exhibited a shift towards higher frequencies, indicating that for the majority of cells, the signaling became less polarized. This observation is consistent with conclusions drawn previously37. We also computed the averaged difference between the curves before and after treatment over 13 cells (Fig. 5F). The biggest difference occurs at low frequency levels, confirming that PI3K inhibition abrogates primarily the polarity in signaling but less so the fine-grained organization (purple arrow in Fig. 5F).
Discussion
Elucidating the organization of molecular distributions and signaling activities on cell surfaces in 3D is confounded by the complexity of relating surface patterns to a reference that allows comparative analyses across cell populations with widely variable morphologies. Here we introduce cellular harmonics to disentangle the differences in surface signal organization from differences in cell morphology. We implemented the Laplace-Beltrami operator (LBO) on individual cell shapes to define a complete basis that spans spatial frequencies and is well adapted to the morphological structures of the cell surface. To parameterize a molecular cell surface pattern, we generated spectra that capture the spatial scale signatures of the pattern.
Previous approaches to quantifying molecular cell surface patterns in the face of cell morphological variation relied on a few global features to represent cell shape or constrained cell shape on micro-patterns11–13. Our work introduces a mathematical construction to characterize the signal organization in a functional space that captures the full range of natural scales relevant to the regulation of molecular processes. Thus, our framework is suitable to experimental conditions, including in vivo imaging, that preclude external control over cell shape. The isometry invariant property of the LBO is often desired in shape matching, preserving the eigenvalue spectrum. Surfaces that change shape via folding without stretching are expected to be isometric across time, rending our framework particularly well-suited for evaluating molecular patterning on individual cells over time (Supplementary Video 1 & 4). In general, the spectral decomposition of surface data enables the measurement and interpretation of the spatial organization of molecular distributions ranging from simulated data, such as signaling distributions on the cell surface, to larger scale phenomena, such as cytoskeletal distributions on embryo surfaces. The framework also provides a mathematically tractable, yet complete, representation to power downstream analyses including generative modeling and machine learning.
The spatial scale of molecular organization is measured by the relative distances between aggregates. However, the spectra are non-informative of the aggregate sizes. This may be a limitation for certain biological applications. The accuracy of the spatial scales depends on the imaging resolution and measurement of marker signal intensity at the mesh surface. All image data presented in this work was Nyquist sampled (voxel side length of 160 nm with an isotropic optical resolution of generally 390 nm after deconvolution)44. Our default segmentation process generates a mesh surface with a number of nodes high enough to preserve the input imaging resolution. Using our framework, we can calculate the LBO for a mesh with ~100K nodes. However, as shown in Supplementary Fig.s 7 and 8A, the energy spectra of a molecular organization are robust in presence of spatial noise in the signal and down-sampling of the mesh. Thus, the proposed method is applicable to diverse image data sets, likely also of lower quality than those illustrated here.
The u-signal3D framework is made available as a collection of MATLAB functions bundled into a user-friendly interface. Underlying the implementation of u-signal3D is a robust computational pipeline for mesh triangulation and determination of LBO eigenvectors using algorithms that cope with both manifold and non-manifold cell geometries24,35,36. The LBO is critical to many computer graphics algorithms. The resources and validation provided by this work will aid the microscopy community in further adapting tools from the computer graphics field.
Methods
Cell culture and imaging.
To validate our workflow, we used movie collections that were generated for previously published studies of various cellular processes. All cells were imaged via high resolution light-sheet microscopy with isotropic resolution40,44. The cell preparation and imaging conditions for the CyOFP-tractin40, NRAS-GFP39, pBOB-Septin2-GFP39, and PI3K activity (GFP-AktPH)37 datasets are available in the previously published papers. To simulate the polka dot patterns on observed cell geometries, we also used 67 cell surfaces from Driscoll et al34. These cell surfaces included 29 dendritic cells expressing Lifeact-GFP, 27 MV3 melanoma cells expressing tractin-GFP, and 11 human bronchial epithelial (HBEC) cells expressing tractin-GFP.
Cell surface generation.
The pipeline embeds the cell surface generation modules from our previously published u-shape3D analysis framework34. 3D raw images of cells were deconvolved using either a Wiener filter with the Wiener parameter set to 0.018 (for CyOFP-tractin, NRAS-GFP and pBOB-Septin2-GFP localization) or a Richardson-Lucy algorithm (for PI3K activity). To reduce deconvolution artifacts, images were apodized, as previously described40. The apodization height parameter set to 0.06 for all data except the PI3K dataset. Then we smoothed the deconvolved images with a 3D Gaussian kernel (only for the PI3K dataset with pixels) and applied a gamma correction (for the PI3K and septin dataset of 0.7, for the NRAS datasets of 0.6, and for CyOFP-tractin of 1). For the segmentation of melanoma cells in the PI3K, septin, and NRAS data sets, we used the ‘twoLevelSurface’ segmentation mode, which combines a blurred image of the cell interior with an automatically thresholded image of the cell surface. For melanoma cells labeled with CyOFP-tractin, cells were segmented at the intensity value specified by the Otsu threshold45. Finally, the triangle mesh representing the cell surface was smoothed using curvature flow smoothing46.
Mesh characterization and validation.
Triangle surface meshes generated from 3D microscopy images are prone to artifacts that adversely impact the Laplace-Beltrami operator output. One such artifact is a multi-component mesh, which often has isolated sets of disconnected triangles that do not correspond to the actual cell geometry (Supplementary Fig. 1A, black arrows), and thus can be safely removed. Connected components of a mesh are identified by a list of mesh faces that share an edge. Smaller components are filtered out by a threshold defined on volume or surface area. For our data, we set the threshold to keep only the largest component of the cell surface. We used the ‘remove_small_components’ function from a public GitHub repository of the geometry processing toolbox [https://github.com/alecjacobson/gptoolbox].
For further processing, the cell surface must be represented as a closed 2-manifold mesh satisfying two conditions: i) each edge is incident to only two faces and ii) at each vertex of a face the face is embedded in a fan (Supplementary Fig. 1B). Since some workflows may generate non-manifold meshes, as an option, we include a state-of-the-art LBO algorithm24 that first creates a manifold mesh, termed a tufted mesh, from the non-manifold mesh, before applying the LBO. In practice, we have not encountered a non-manifold mesh generated by our framework, thus we use the standard approach to compute the LBO, described below, by default.
Intensity measurement.
We measured the fluorescence intensity local to each mesh vertex from the raw image. The cytosolic background noise was first removed by subtracting the median pixel intensity inside the cell. Then, at each vertex, the average pixel intensity was computed within a sampling radius of 1 μm over the pixels inside the cell. Finally, we normalized each cell’s surface intensity to a mean of one.
Laplace-Beltrami calculation.
The cell surface geometry is defined by vectors of N triangle mesh vertices in a Cartesian coordinate system. The mesh vertices are connected in triangles to form mesh faces. To create a set of basis functions for a cell, we applied the Laplace-Beltrami operator (LBO) to the mesh. The LBO is a second-order differential operator defined as the divergence of the gradient of a function. On a triangle mesh, it computes the geometrical variation of the surface from a sphere. Mathematically, we aim to solve the following eigendecomposition equation to obtain the eigenvectors and eigenvalues of the LBO on a given mesh:
| (1) |
Here denotes the i-th eigenvector corresponding to the i-th eigenvalue, , of the Laplacian operator,.
The Laplacian operator acting on an arbitrary discrete mesh has been extensively studied15,23,35,36,46–49. Most computational approaches are based on the cotangent scheme35,36, which is a form of first order finite element method applied to the Laplacian operator on a surface. In the cotangent formula (C), the LBO is an NxN symmetric matrix:
| (2) |
where are the two angles relative to edge as indicated in Supplementary Fig. 1Bii. For the matrix element , the index runs over all vertices connected to vertex through an edge .
To obtain the LBO eigenvectors and eigenvalues, we used the function eigs() in MATLAB. The eigenvectors are frequency-based hierarchical functions that follow the protrusions of the 3D shape, respecting their symmetries. For example, for a sphere the eigenvalues of the first frequency level () are identical and correspond to three eigenvectors oriented in three orthogonal directions in 3D space. When the LBO is applied to an ellipsoid, where the symmetry is broken in one direction, the eigenvalue has higher magnitude in the short ellipsoid axis direction. Eigenvectors at the higher frequency levels follow the symmetry breaks of the ellipsoid to capture the shape variation relative to a sphere. In analogy, for a complex shape, the LBO eigenvectors follow the variation of the surface relative to a sphere (Fig. 2C).
Computation time depends on the number of LBO eigenvectors, which determines the frequency upper limit. Measuring the energy spectra up to L = 50 requires a few minutes. For raw images, additional time is needed for the cell segmentation process.
Representation of cell surface signals using LBO eigenvectors.
Eigenvectors () of the Laplacian constitute an orthogonal complete basis set. Thus, we can extend a surface signal in this basis,
| (3) |
where is the number of Laplacian eigenvectors and is the Laplacian eigenprojection of the i-th eigenvector. The eigenprojections determine the contribution of each cell geometry defined eigenvector in parameterizing the signal . Based on the LBO eigenvectors and eigenprojections of a signal, the signal can be recreated (). To do so, we summed up the eigenprojections, multiplying each by the corresponding eigenvector in order to reconstruct the signal. To assess the reconstructed signal with its original values, we computed the absolute error ratio given by,
| (4) |
LB frequency level measurement.
Application of the LBO (equation (1)) to a perfect sphere yields the spherical harmonics, , as shown in a frequency level pyramid with the first levels shown in Fig. 2B. In spherical coordinates, the spherical harmonics are given by
| (5) |
in which, define the colatitude and longitude, respectively; the indices and indicate the degree and order of the function in frequency-based levels; and are the Legendre polynomials. The LBO encodes both the spatial angular frequency and its orientation over the eigenvectors.
Each frequency level has eigenvectors with similar spatial angular frequency. As an example, the second level () of spherical harmonics has three identical eigenvectors corresponding to three harmonics, capturing three orthogonal spatial direction (Fig. 2B). Higher level basis functions capture a greater number of pseudo-orientations with equal spatial scale. To quantify the spatial angular scale of a signal on a mesh surface, we collapsed the measurements from individual eigenvectors (frequency index) to a single value per level (frequency level), as we explain in the next section. Seeking to separate scale and pseudo-orientational information, we turned to a quantum mechanical interpretation of the spherical harmonics. The electron orbitals of an atom are simply described by the spherical harmonics pyramid shown in Fig. 2B, with each level of the pyramid corresponding to a distinct electron energy. Indeed, mathematically all orbitals belonging to the same level have the same spatial angular frequency.
Although for complicated 3D shapes with lower symmetry compared to a sphere, eigenvectors at the same frequency levels have different eigenvalues, it is still reasonable to smooth the measurement over each level () to extract the spatial scale signature of a given molecular organization.
Dirichlet energy calculation.
In computer geometry and shape analysis, the Dirichlet energy is often used as a metric of the smoothness of a function defined in a region50. The Dirichlet energy is given by
| (6) |
where is a function defined on the region in three dimensions . Integration by parts yields,
| (7) |
The first term on the right hand side is the Laplacian of the in the region, and the second term relates to the boundary conditions. For a closed surface, such as a segmented cell, this term vanishes.
Substituting for subject to equation (1) and under consideration of the orthogonality of the LBO eigenvectors, the energy term equation (7) turns into,
| (8) |
The Dirichlet energy in (8) is a scalar parameter. In our framework, the energy is computed per spatial angular frequency level to obtain an energy spectra. The energy per frequency level follows
| (9) |
where is the first index of the eigenvector at frequency level . Similar to quantum physics, the term gives the probability of the i-th eigenvector contributing to the signal function while is the eigenvalue corresponding to the eigenvector . As mentioned above, the eigenprojections per level indicate the dominant spatial scale of a given molecular organization without regard to shape symmetry variation. Since fluorescence expression can vary from cell to cell, we normalized the energy spectra to 1 by dividing by the total energy ( in equation (8)) to define an energy density spectra for each cell that can be compared across a cell population.
Polka dot generation.
We simulated polka dot patterns to validate the spatial scale of the measured signal distribution on a given mesh. As shown in Supplementary Fig. 5A, to generate uniform polka dot distributions, dot centers, or seeds, were first found by maximizing the minimum pairwise Euclidean distance amongst seeds. We used the ‘farthest_point’ function from a public GitHub repository of the geometry processing toolbox [https://github.com/alecjacobson/gptoolbox/external/toolbox_fast_marching]. Then we calculated the geodesic distance of all vertices from the closest seed using the fast marching method51. The polka dot pattern was then created by thresholding the surface over the list of geodesic distances, such that the fraction of total surface area occupied by polka dots was maintained across patterns. For the presented data, we found that 30% of the entire cell surface area has a higher energy peak magnitude for the polka dot surface area (Supplementary Fig. 3C). We set the edge mode parameter in the framework to ‘sharp’ for binary patterns and ‘smooth’ for gray patterns (Supplementary Fig. 3).
The generation of patchy polka dot patterns was similar to that of uniform polka dot patterns, except we kept only one quarter of the pattern on one side of the cell surface. For non-uniform polka dot patterns, we randomly chose mesh vertices for dot centers and grew the seeds as mentioned above.
Noise generation.
We generated two kinds of noise, i) intensity noise and ii) spatial noise. In the first case, we added a random intensity value to each mesh node drawn from a uniform distribution in the range of zero to a variable upper limit. We adjusted the noise level by changing the upper limit to a factor of the maximum intensity of either the polka dot pattern or the molecular organization. For the spatial noise, we translocated the mesh node values of painted area to a random node in a predefined neighborhood. The number of iteration for translocating each mesh node value was randomly selected from a Gaussian distribution with a standard deviation proportional to dot size. We controlled the noise level by changing the standard deviation of gaussian distribution.
Measuring the upper limit of the frequency level.
The Laplace-Beltrami operator is scale invariant. To measure the average distance between molecular aggregations on the cell surface, we painted the cell with various uniform polka dot distributions. The distance between dot centers was next calculated as the square root of surface area divided by the number of polka dots (Supplementary Fig. 8C). Depending on the cell surface, the energy peak levels vary with the number of polka dots, which corresponds to the distance between dots.
Texture mapping.
We mapped the molecular (NRAS) organization from one melanoma cell surface to another using a texture mapping algorithm, orbifold-Tutte embeddings42. First, we chose four positional constraints on each mesh at top and bottom of the mesh by choosing from the minimum and maximum mesh node coordinates. Then we used the ‘Parallelogram’ mode for finding the mapping matrix. Finally, we mapped a pattern from the mapped mesh to the primary mesh using the transpose of the mapping matrix.
Polka dot clustering.
We constructed four polka dot patterns with 16, 64, 256, and 1024 dots respectively on each of the 67 cell morphologies. For each pattern, we compiled a feature vector composed of the energy density spectra and then performed principal component (PC) analysis. The first three components contributed 58% of the total variance in the 77-dimensional feature space. To cluster the polka dot patterns, we employed the k-means algorithm in the 3D PC space. The number of clusters was optimized to four using the silhouette distance. We calculated the mean of silhouette distances for each data point across each cluster, obtained by k-means clustering for cluster numbers ranging from 2 to 10.
Statistical analysis of drug inhibition.
We used the two-sided Kolmogorov-Smirnov (KS) test to evaluate the septin energy spectra under WGA treatment. We calculated the p-value between the averaged energy spectra of untreated and treated cells.
To quantify the redistribution of PI3K activity after PI3K inhibition, we compared the energy spectra of individual cells before and after inhibition. We measured the median frequency level of each curve because the value of the energy spectra at higher frequencies is dominant by noise and the distribution is more skewed rather than a normal distribution. We then computed the difference in the median before and after inhibition for 13 cells (Fig. 5E). Additionally, to evaluate the energy spectra over the entire frequency range, we averaged the difference curves between the before and after inhibition conditions for the 13 cells (Fig. 5F).
Visualization
3D surface renderings of single cells were generated with ChimeraX version 1.2.552 and some schematics were adapted from “Cancer Cells” by BioRender.com (2022). ImageJ/Fiji was employed to prepare the MIP and slice images53.
Supplementary Material
Supplementary Fig. 1. Triangle mesh representation. A. Surface renderings of a human bronchial epithelial cell (HBEC). The cell surface was generated from the tractin-GFP-signal visualizing cortical actin filament structures (data not shown). Multiple mesh components are visible. They are automatically filtered by the u-signal3D software. B.i. Manifold and non-manifold edges and vertices in a triangle mesh. B.ii. Two faces of a triangle mesh. and are the angles corresponding to the i-th and j-th vertices in the cotangent Laplacian method.
Supplementary Video 1. Molecular distribution over time. Surface rendering of an MV3 melanoma cell expressing GFP-AktPH, a marker of PI3K activity. Red color indicates regions of high signaling activity and yellow color regions of low activity (see the color bar in Fig. 1B).
Supplementary Fig. 2. Reconstructing surface signal data from the spectral decomposition. A.i. PI3K activity biosensor intensity (GFP-AktPH) projected onto MV3 melanoma cells. A.ii. LBO eigenvectors () corresponding to the shown PI3K activity are organized hierarchically from low frequency level () to high frequency level. A.iii. Color scale is adjusted for visualizing the high-frequency variations (L =10). B. Absolute error ratio between the reconstructed surface signal distributions and the original PI3K activity biosensor intensity as a function of the number of frequency levels included in the reconstruction. C. PI3K activity (GFP-AktPH) projected onto the MV3 melanoma cell in (A) with the original data (i) shown compared to the low-pass filtered signal up to level L=10 (ii).
Supplementary Video 2. 3D molecular organization of cytosol marker and CyOFP-tractin at the surface of an MV3 melanoma cell. Surface rendering of an MV3 melanoma cell expressing cytosolic GFP and CyOFP-tractin (see Fig 4A).
Supplementary Video 3. 3D raw image of cytosol marker and CyOFP-tractin on an MV3 melanoma cell. Maximum intensity projection along the y-axis of raw volumetric of cytosolic GFP and CyOFP-tractin signals onto the cell surface(see Fig 4A).Both signals display patchy organization, however the CyOFP-tractin signal is more structured, as expected.
Supplementary Video 4. PI3K activity redistribution on an MV3 melanoma cell under PI3K inhibition. Surface rendering of an MV3 melanoma cell expressing GFP-AktPH, a marker of PI3K activity, after adding PI3K inhibitor (left). Energy density spectra of the PI3K activity redistribution under PI3K inhibition.
Supplementary Fig. 3. Polka dot pattern generation. A. Surface rendering of an MV3 melanoma cell (top). The same cell surface painted with centers for 64 dots (middle); the dots are grown radially from the centers until they cover30% of the cell surface area (bottom). B. Surface rendering of the N = 64 polka dot pattern with a sharp edge (left), 25% (middle) and 50 % (right) smoothed edges (top). Corresponding energy density spectra (bottom). C. Surface rendering of the N = 64 polka dot pattern painting 10%, 30%, 50%, 60% of the total surface area (top). Corresponding energy density spectra (bottom). Inset shows energy spectra of patterns covering 2.5%, 5%, 7.5 % of total surface area. D. Polka dot patterns with 64 dots applied to a sphere (left) and two ellipsoids with eccentricity e = 0.75 (middle) and e = 0.5 (right) (top). Corresponding energy density spectra (bottom).
Supplementary Fig. 4. The Laplace-Beltrami operator (LBO) on symmetric shapes. A. Examples of LBO eigenvectors of a sphere at frequency level L=4 in back and front views. The number of peaks in the eigenvector magnitude is 3 (left) and 4 (right). B. Examples of LBO eigenvectors of a sphere (back and front visualization) that have 4 peaks in magnitude, at frequency levels L = 4 (left) and 5 (right).
Supplementary Fig. 5. Cell surface library. Surface renderings of MV3 melanoma cells with blebs (1–27), dendritic cells with lamellipodia (28–56), and HBEC cells with filopodia (57–67). The cell surfaces were generated from the tractin-GFP (MV3 cells, HBEC) or Lifeact-GFP intensity (dendritic cells).
Supplementary Fig. 6. Non-homogenous polka dot patterns. A. Patchy polka dot patterns. A.i. Patterns with 64 dots homogenously distributed on the cell (left), on one quarter of the back side (middle) and on one quarter of the front side (right) with 16 dots. A.ii. Corresponding energy density spectra (left). Ratio of energy density spectra between full cell and quarter cell region patterns (right). B. Combination of two polka dot patterns. B.i. Combined patterns with 16 and 1024 dots covering 30% of the total surface area (left), and individual patterns with N = 16 (middle) and N =1024 (right) dots. B.ii. Energy density spectra of combined pattern (top) and individual patterns (bottom). C. Randomly distributed polka dot patterns. C.i. Polka dots are randomly painted on the cell surface; patterns with N = 128, 256, 512, and 1024 dots. C.ii. Energy density spectra of patterns with random (top) and homogenous (bottom) dot distributions. Shaded bands are the minimum and maximum energy spectra for each level across 20 sets of random dot centers for each pattern. Bold curves indicate the mean of the energy density per level for each pattern across 20 repetitions with random dot centers.
Supplementary Fig. 7. Noise on polka dot pattern. A. Random signal with values sampled from a homogenous distribution in the interval 0 to 1 on an MV3 melanoma cell surface (top). Corresponding energy density spectra (bottom). B. Homogenous pattern of N = 64 dots on the same cell surface with intensity noise sampled from a homogenous random distribution with a range 0% (left), 50% (middle) and 100% (right) of the polka dot value (top). Corresponding energy density spectra (bottom). C.i. Smooth homogenous pattern of N= 64 dots on the same cell surface with intensity noise sampled from a homogenous random distribution with a maximum, from left to right, of 0, 2, 6 and 10 times the polka dot value. C.ii. Standard deviation of intensity for the total pattern (blue) and homogenous random noise (red). C.iii. Corresponding energy density spectra. D. Smooth homogenous pattern of N= 1024 dots on the same cell surface with intensity noise sampled from a random distribution with, from left to right, a maximum of 0, 2, 6, 10 times the maximum polka dot value (top). Corresponding energy density spectra (bottom). E. GFP-AKtPH signal perturbed by intensity noise sampled from a uniform random distribution with a maximum, from left to right, of 0, 0.25, 0.75, and 1 times the range of the fluorescent signal. F. Homogenous pattern of N= 64 dots on the same cell surface perturbed by random translocation of the value of a mesh node to another node within a circular neighborhood of radius, from left to right, 0, 0.018, 1.8, and 18 times the dot size (top) and corresponding energy density spectra(bottom).
Supplementary Fig. 8. Molecular organization on MV3 cell population. A. Mesh resolution. Triangle mesh representing the surface of an MV3 melanoma cell, expressing GFP-AktPH (left). Mesh vertices are reduced by a factor of 10 (right). Energy density spectra of PI3K activity on the original mesh surface (blue) and on the mesh surface reduced by a factor of 10 (red) and 100 (yellow). B. Energy density spectra of a cytosolic marker (blue curve), CyOFP-tractin (red curve), and the binary on-/off-bleb distribution (yellow) for five melanoma cells imaged under identical experimental conditions. Bold curves indicate the mean of the five individual spectra. Shaded bands are the minimum and maximum energy spectra for each level across five cells. C. Geodesic distance between the polka dots on the surface of MV3 melanoma cells (presented in Fig. 4, number of cells = 11) as a function of energy peak level. The polka dots painted on each mesh, are 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, or 1024. Star markers indicate the averaged peak levels across 11 cells. The dashed line illustrates the 1 μm sampling radius for surface signals. D. Energy density spectra of NRAS localization (blue curve) and the binary on-/off-bleb distribution (red) for six melanoma cells imaged under identical experimental conditions. Bold curves indicate the mean of the six individual spectra. Shaded bands are the minimum and maximum energy spectra for each level across six cells.
Supplementary Fig. 9. NRAS-GFP localization and bleb distribution. Surface rendering of six MV3 melanoma cells, showing NRAS-GFP signal and bleb distribution segmented by u-shape3D software (left). Blebs are shown dark gray with white areas in between. Energy density spectra of NRAS signal and bleb distribution (middle). Ratio of NRAS to bleb spectra (right).
Supplementary Fig. 10. Pattern mapping. A. Polka dot pattern on an MV3 melanoma cell with N = 16 dots (left). Polka dot pattern mapped onto a new MV3 melanoma cell surface (right) using an orbifold Tutte embedding texture mapper. Energy density spectra of original (blue) and mapped (red) patterns (bottom). B. NRAS localization on five MV3 melanoma cells (left) mapped onto the surface of five new MV3 melanoma cells (middle). Energy density spectra of the original (blue) and mapped signal distributions (red).
Acknowledgments
We would like to thank Maks Ovsjanikov, Jungsik Noh, Felix Zhou, and Jaewon Huh for fruitful discussions. We would like to thank Andrew Weems, Erik Welf, Reto Fiolka, and Kevin Dean for data collection. This work was supported by the following grants: K99GM123221 to MKD; R35GM136428 and RM1GM145399 to GD.
Footnotes
Ethics declarations
The authors declare no competing interests.
Code Availability
All analysis was performed in a custom software package (u-signal3D) written in MATLAB (Mathworks), which is available as a frozen version in a Zenodo repository (https://doi.org/10.5281/zenodo.8222824)55 and as an updated repository at (https://github.com/DanuserLab/u-signal3D).
Data Availability
All image data that support the findings of this study are available in a Zenodo repository (https://doi.org/10.5281/zenodo.8166238)54. This repository comprises a collection of high-resolution 3D cell images captured using light sheet microscopy. These images have been previously published, and the origin of the dataset is referenced in the Methods section. Source data for Figs 2–5 are provided with this manuscript.
References
- 1.Jordan JD, Landau EM & Iyengar R Signaling networks: the origins of cellular multitasking. Cell 103, 193–200 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kholodenko BN Cell-signalling dynamics in time and space. Nature reviews Molecular cell biology 7, 165–176 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Neves SR et al. Cell shape and negative links in regulatory motifs together control spatial information flow in signaling networks. Cell 133, 666–680 (2008). 10.1016/j.cell.2008.04.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jaqaman K & Ditlev JA Biomolecular condensates in membrane receptor signaling. Current Opinion in Cell Biology 69, 48–54 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Edidin M Patches, posts and fences: proteins and plasma membrane domains. Trends Cell Biol 2, 376–380 (1992). 10.1016/0962-8924(92)90050-w [DOI] [PubMed] [Google Scholar]
- 6.Schmick M & Bastiaens PIH The interdependence of membrane shape and cellular signal processing. Cell 156, 1132–1138 (2014). 10.1016/j.cell.2014.02.007 [DOI] [PubMed] [Google Scholar]
- 7.Driscoll MK & Danuser G Quantifying Modes of 3D Cell Migration. Trends Cell Biol 25, 749–759 (2015). 10.1016/j.tcb.2015.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Elliott H et al. Myosin II controls cellular branching morphogenesis and migration in three dimensions by minimizing cell-surface curvature. Nat Cell Biol 17, 137–147 (2015). 10.1038/ncb3092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.O’Shaughnessy EC et al. Software for lattice light-sheet imaging of FRET biosensors, illustrated with a new Rap1 biosensor. J Cell Biol 218, 3153–3160 (2019). 10.1083/jcb.201903019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Peng HC Bioimage informatics: a new area of engineering biology. Bioinformatics 24, 1827–1836 (2008). 10.1093/bioinformatics/btn346 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schauer K et al. Probabilistic density maps to study global endomembrane organization. Nature Methods 7, 560–U111 (2010). 10.1038/Nmeth.1462 [DOI] [PubMed] [Google Scholar]
- 12.Biot E et al. Strategy and software for the statistical spatial analysis of 3D intracellular distributions. Plant J 87, 230–242 (2016). 10.1111/tpj.13189 [DOI] [PubMed] [Google Scholar]
- 13.Pecot T, Zengzhen L, Boulanger J, Salamero J & Kervrann C A quantitative approach for analyzing the spatio-temporal distribution of 3D intracellular events in fluorescence microscopy. Elife 7 (2018). 10.7554/eLife.32311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Peng T & Murphy RF Image-derived, three-dimensional generative models of cellular organization. Cytometry Part A 79, 383–391 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Taubin G in Proceedings of the 22nd annual conference on Computer graphics and interactive techniques. 351–358. [Google Scholar]
- 16.Vallet B & Lévy B in Comput Graph Forum. 251–260 (Wiley Online Library; ). [Google Scholar]
- 17.Reuter M, Wolter F-E & Peinecke N Laplace–Beltrami spectra as ‘Shape-DNA’of surfaces and solids. Computer-Aided Design 38, 342–366 (2006). [Google Scholar]
- 18.Ducroz C, Olivo-Marin JC & Dufour A Characterization of Cell Shape and Deformation in 3d Using Spherical Harmonics. 2012 9th Ieee International Symposium on Biomedical Imaging (Isbi), 848–851 (2012). [Google Scholar]
- 19.Cammarasana S & Patane G Localised and shape-aware functions for spectral geometry processing and shape analysis: A survey & perspectives. Comput Graph-Uk 97, 1–18 (2021). 10.1016/j.cag.2021.03.006 [DOI] [Google Scholar]
- 20.Choukroun Y, Shtern A, Bronstein A & Kimmel R Hamiltonian Operator for Spectral Shape Analysis. Ieee T Vis Comput Gr 26, 1320–1331 (2020). 10.1109/Tvcg.2018.2867513 [DOI] [PubMed] [Google Scholar]
- 21.Melzi S, Rodola E, Castellani U & Bronstein MM Localized Manifold Harmonics for Spectral Shape Analysis. Comput Graph Forum 37, 20–34 (2018). 10.1111/cgf.13309 [DOI] [Google Scholar]
- 22.Neumann T, Varanasi K, Theobalt C, Magnor M & Wacker M Compressed Manifold Modes for Mesh Processing. Comput Graph Forum 33, 35–44 (2014). 10.1111/cgf.12429 [DOI] [Google Scholar]
- 23.Belkin M, Sun J & Wang YS Discrete Laplace Operator on Meshed Surfaces. Proceedings of the Twenty-Fourth Annual Symposium on Computational Geometry (Sgg’08), 278–287 (2008). 10.1145/1377676.1377725 [DOI] [Google Scholar]
- 24.Sharp N & Crane K A Laplacian for Nonmanifold Triangle Meshes. Comput Graph Forum 39, 69–80 (2020). 10.1111/cgf.14069 [DOI] [Google Scholar]
- 25.Petronetto F, Paiva A, Helou ES, Stewart DE & Nonato LG Mesh-Free Discrete Laplace-Beltrami Operator. Comput Graph Forum 32, 214–226 (2013). 10.1111/cgf.12086 [DOI] [Google Scholar]
- 26.Angenent S, Haker S, Tannenbaum A & Kikinis R On the Laplace-Beltrami operator and brain surface flattening. IEEE transactions on medical imaging 18, 700–711 (1999). [DOI] [PubMed] [Google Scholar]
- 27.Klein A et al. Mindboggling morphometry of human brains. PLoS computational biology 13, e1005350 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Graichen U et al. SPHARA--a generalized spatial Fourier analysis for multi-sensor systems with non-uniformly arranged sensors: application to EEG. PLoS One 10, e0121741 (2015). 10.1371/journal.pone.0121741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Huang SG, Chung MK, Qiu A & Alzheimer’s Disease Neuroimaging I Fast mesh data augmentation via Chebyshev polynomial of spectral filtering. Neural Netw 143, 198–208 (2021). 10.1016/j.neunet.2021.05.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Qiu A, Bitouk D & Miller MI Smooth functional and structural maps on the neocortex via orthonormal bases of the Laplace-Beltrami operator. IEEE Trans Med Imaging 25, 1296–1306 (2006). 10.1109/tmi.2006.882143 [DOI] [PubMed] [Google Scholar]
- 31.Ruan X & Murphy RF Evaluation of methods for generative modeling of cell and nuclear shape. Bioinformatics 35, 2475–2485 (2019). 10.1093/bioinformatics/bty983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shen L, Farid H & McPeek MA Modeling Three-Dimensional Morphological Structures Using Spherical Harmonics. Evolution 63, 1003–1016 (2009). 10.1111/j.1558-5646.2008.00557.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Viana MP et al. Integrated intracellular organization and its variations in human iPS cells. Nature 613, 345–354 (2023). 10.1038/s41586-022-05563-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Driscoll MK et al. Robust and automated detection of subcellular morphological motifs in 3D microscopy images. Nat Methods 16, 1037–1044 (2019). 10.1038/s41592-019-0539-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pinkall U & Polthier K Computing discrete minimal surfaces and their conjugates. Experimental mathematics 2, 15–36 (1993). [Google Scholar]
- 36.Ovsjanikov M et al. in SIGGRAPH ASIA 2016 Courses 1–60 (2016). [Google Scholar]
- 37.Driscoll MK et al. Proteolysis-free cell migration through crowded environments via mechanical worrying. bioRxiv, 2020.2011. 2009.372912 (2022). [Google Scholar]
- 38.Ronchi V Forty years of history of a grating interferometer. Applied optics 3, 437–451 (1964). [Google Scholar]
- 39.Weems AD et al. Blebs promote cell survival by assembling oncogenic signalling hubs. Nature 615, 517–525 (2023). 10.1038/s41586-023-05758-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Welf ES et al. Quantitative Multiscale Cell Imaging in Controlled 3D Microenvironments. Dev Cell 36, 462–475 (2016). 10.1016/j.devcel.2016.01.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Charras G & Paluch E Blebs lead the way: how to migrate without lamellipodia. Nature reviews Molecular cell biology 9, 730–736 (2008). [DOI] [PubMed] [Google Scholar]
- 42.Aigerman N & Lipman Y Orbifold tutte embeddings. ACM Trans. Graph. 34, 190:191–190:112 (2015). [Google Scholar]
- 43.Charras GT, Coughlin M, Mitchison TJ & Mahadevan L Life and times of a cellular bleb. Biophys J 94, 1836–1853 (2008). 10.1529/biophysj.107.113605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dean KM, Roudot P, Welf ES, Danuser G & Fiolka R Deconvolution-free subcellular imaging with axially swept light sheet microscopy. Biophysical journal 108, 2807–2815 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Otsu N A threshold selection method from gray-level histograms. IEEE transactions on systems, man, and cybernetics 9, 62–66 (1979). [Google Scholar]
- 46.Desbrun M, Meyer M, Schroder P & Barr AH Implicit fairing of irregular meshes using diffusion and curvature flow. Comp Graph, 317–324 (1999). [Google Scholar]
- 47.Demanet L Painless, highly accurate discretizations of the Laplacian on a smooth manifold. (Technical report, Stanford University, 2006). [Google Scholar]
- 48.Mayer UF Numerical solutions for the surface diffusion flow in three space dimensions. Computational and Applied Mathematics 20, 361–379 (2001). [Google Scholar]
- 49.Xu G Discrete Laplace–Beltrami operators and their convergence. Computer aided geometric design 21, 767–784 (2004). [Google Scholar]
- 50.Solomon J, Guibas L & Butscher A in Comput Graph Forum. 197–206 (Wiley Online Library; ). [Google Scholar]
- 51.Sethian JA Fast marching methods. SIAM review 41, 199–235 (1999). [Google Scholar]
- 52.Goddard TD et al. UCSF ChimeraX: Meeting modern challenges in visualization and analysis. Protein Science 27, 14–25 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Schneider CA, Rasband WS & Eliceiri KW NIH Image to ImageJ: 25 years of image analysis. Nat Methods 9, 671–675 (2012). 10.1038/nmeth.2089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mazloom-Farsibaf H, Zou Q, Hsieh R, Driscoll MK & Danuser G Data repository supporting “Cellular Harmonics for the Morphology-invariant Analysis of Molecular Organization at the Cell Surface”. Zenodo (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zou Q DanuserLab/u-signal3D. Zenodo (2023). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Fig. 1. Triangle mesh representation. A. Surface renderings of a human bronchial epithelial cell (HBEC). The cell surface was generated from the tractin-GFP-signal visualizing cortical actin filament structures (data not shown). Multiple mesh components are visible. They are automatically filtered by the u-signal3D software. B.i. Manifold and non-manifold edges and vertices in a triangle mesh. B.ii. Two faces of a triangle mesh. and are the angles corresponding to the i-th and j-th vertices in the cotangent Laplacian method.
Supplementary Video 1. Molecular distribution over time. Surface rendering of an MV3 melanoma cell expressing GFP-AktPH, a marker of PI3K activity. Red color indicates regions of high signaling activity and yellow color regions of low activity (see the color bar in Fig. 1B).
Supplementary Fig. 2. Reconstructing surface signal data from the spectral decomposition. A.i. PI3K activity biosensor intensity (GFP-AktPH) projected onto MV3 melanoma cells. A.ii. LBO eigenvectors () corresponding to the shown PI3K activity are organized hierarchically from low frequency level () to high frequency level. A.iii. Color scale is adjusted for visualizing the high-frequency variations (L =10). B. Absolute error ratio between the reconstructed surface signal distributions and the original PI3K activity biosensor intensity as a function of the number of frequency levels included in the reconstruction. C. PI3K activity (GFP-AktPH) projected onto the MV3 melanoma cell in (A) with the original data (i) shown compared to the low-pass filtered signal up to level L=10 (ii).
Supplementary Video 2. 3D molecular organization of cytosol marker and CyOFP-tractin at the surface of an MV3 melanoma cell. Surface rendering of an MV3 melanoma cell expressing cytosolic GFP and CyOFP-tractin (see Fig 4A).
Supplementary Video 3. 3D raw image of cytosol marker and CyOFP-tractin on an MV3 melanoma cell. Maximum intensity projection along the y-axis of raw volumetric of cytosolic GFP and CyOFP-tractin signals onto the cell surface(see Fig 4A).Both signals display patchy organization, however the CyOFP-tractin signal is more structured, as expected.
Supplementary Video 4. PI3K activity redistribution on an MV3 melanoma cell under PI3K inhibition. Surface rendering of an MV3 melanoma cell expressing GFP-AktPH, a marker of PI3K activity, after adding PI3K inhibitor (left). Energy density spectra of the PI3K activity redistribution under PI3K inhibition.
Supplementary Fig. 3. Polka dot pattern generation. A. Surface rendering of an MV3 melanoma cell (top). The same cell surface painted with centers for 64 dots (middle); the dots are grown radially from the centers until they cover30% of the cell surface area (bottom). B. Surface rendering of the N = 64 polka dot pattern with a sharp edge (left), 25% (middle) and 50 % (right) smoothed edges (top). Corresponding energy density spectra (bottom). C. Surface rendering of the N = 64 polka dot pattern painting 10%, 30%, 50%, 60% of the total surface area (top). Corresponding energy density spectra (bottom). Inset shows energy spectra of patterns covering 2.5%, 5%, 7.5 % of total surface area. D. Polka dot patterns with 64 dots applied to a sphere (left) and two ellipsoids with eccentricity e = 0.75 (middle) and e = 0.5 (right) (top). Corresponding energy density spectra (bottom).
Supplementary Fig. 4. The Laplace-Beltrami operator (LBO) on symmetric shapes. A. Examples of LBO eigenvectors of a sphere at frequency level L=4 in back and front views. The number of peaks in the eigenvector magnitude is 3 (left) and 4 (right). B. Examples of LBO eigenvectors of a sphere (back and front visualization) that have 4 peaks in magnitude, at frequency levels L = 4 (left) and 5 (right).
Supplementary Fig. 5. Cell surface library. Surface renderings of MV3 melanoma cells with blebs (1–27), dendritic cells with lamellipodia (28–56), and HBEC cells with filopodia (57–67). The cell surfaces were generated from the tractin-GFP (MV3 cells, HBEC) or Lifeact-GFP intensity (dendritic cells).
Supplementary Fig. 6. Non-homogenous polka dot patterns. A. Patchy polka dot patterns. A.i. Patterns with 64 dots homogenously distributed on the cell (left), on one quarter of the back side (middle) and on one quarter of the front side (right) with 16 dots. A.ii. Corresponding energy density spectra (left). Ratio of energy density spectra between full cell and quarter cell region patterns (right). B. Combination of two polka dot patterns. B.i. Combined patterns with 16 and 1024 dots covering 30% of the total surface area (left), and individual patterns with N = 16 (middle) and N =1024 (right) dots. B.ii. Energy density spectra of combined pattern (top) and individual patterns (bottom). C. Randomly distributed polka dot patterns. C.i. Polka dots are randomly painted on the cell surface; patterns with N = 128, 256, 512, and 1024 dots. C.ii. Energy density spectra of patterns with random (top) and homogenous (bottom) dot distributions. Shaded bands are the minimum and maximum energy spectra for each level across 20 sets of random dot centers for each pattern. Bold curves indicate the mean of the energy density per level for each pattern across 20 repetitions with random dot centers.
Supplementary Fig. 7. Noise on polka dot pattern. A. Random signal with values sampled from a homogenous distribution in the interval 0 to 1 on an MV3 melanoma cell surface (top). Corresponding energy density spectra (bottom). B. Homogenous pattern of N = 64 dots on the same cell surface with intensity noise sampled from a homogenous random distribution with a range 0% (left), 50% (middle) and 100% (right) of the polka dot value (top). Corresponding energy density spectra (bottom). C.i. Smooth homogenous pattern of N= 64 dots on the same cell surface with intensity noise sampled from a homogenous random distribution with a maximum, from left to right, of 0, 2, 6 and 10 times the polka dot value. C.ii. Standard deviation of intensity for the total pattern (blue) and homogenous random noise (red). C.iii. Corresponding energy density spectra. D. Smooth homogenous pattern of N= 1024 dots on the same cell surface with intensity noise sampled from a random distribution with, from left to right, a maximum of 0, 2, 6, 10 times the maximum polka dot value (top). Corresponding energy density spectra (bottom). E. GFP-AKtPH signal perturbed by intensity noise sampled from a uniform random distribution with a maximum, from left to right, of 0, 0.25, 0.75, and 1 times the range of the fluorescent signal. F. Homogenous pattern of N= 64 dots on the same cell surface perturbed by random translocation of the value of a mesh node to another node within a circular neighborhood of radius, from left to right, 0, 0.018, 1.8, and 18 times the dot size (top) and corresponding energy density spectra(bottom).
Supplementary Fig. 8. Molecular organization on MV3 cell population. A. Mesh resolution. Triangle mesh representing the surface of an MV3 melanoma cell, expressing GFP-AktPH (left). Mesh vertices are reduced by a factor of 10 (right). Energy density spectra of PI3K activity on the original mesh surface (blue) and on the mesh surface reduced by a factor of 10 (red) and 100 (yellow). B. Energy density spectra of a cytosolic marker (blue curve), CyOFP-tractin (red curve), and the binary on-/off-bleb distribution (yellow) for five melanoma cells imaged under identical experimental conditions. Bold curves indicate the mean of the five individual spectra. Shaded bands are the minimum and maximum energy spectra for each level across five cells. C. Geodesic distance between the polka dots on the surface of MV3 melanoma cells (presented in Fig. 4, number of cells = 11) as a function of energy peak level. The polka dots painted on each mesh, are 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, or 1024. Star markers indicate the averaged peak levels across 11 cells. The dashed line illustrates the 1 μm sampling radius for surface signals. D. Energy density spectra of NRAS localization (blue curve) and the binary on-/off-bleb distribution (red) for six melanoma cells imaged under identical experimental conditions. Bold curves indicate the mean of the six individual spectra. Shaded bands are the minimum and maximum energy spectra for each level across six cells.
Supplementary Fig. 9. NRAS-GFP localization and bleb distribution. Surface rendering of six MV3 melanoma cells, showing NRAS-GFP signal and bleb distribution segmented by u-shape3D software (left). Blebs are shown dark gray with white areas in between. Energy density spectra of NRAS signal and bleb distribution (middle). Ratio of NRAS to bleb spectra (right).
Supplementary Fig. 10. Pattern mapping. A. Polka dot pattern on an MV3 melanoma cell with N = 16 dots (left). Polka dot pattern mapped onto a new MV3 melanoma cell surface (right) using an orbifold Tutte embedding texture mapper. Energy density spectra of original (blue) and mapped (red) patterns (bottom). B. NRAS localization on five MV3 melanoma cells (left) mapped onto the surface of five new MV3 melanoma cells (middle). Energy density spectra of the original (blue) and mapped signal distributions (red).
Data Availability Statement
All image data that support the findings of this study are available in a Zenodo repository (https://doi.org/10.5281/zenodo.8166238)54. This repository comprises a collection of high-resolution 3D cell images captured using light sheet microscopy. These images have been previously published, and the origin of the dataset is referenced in the Methods section. Source data for Figs 2–5 are provided with this manuscript.


