Abstract
Partly interval-censored data often occur in cancer clinical trials and have been analyzed as right-censored data. Patients’ geographic information sometimes is also available and can be useful in testing treatment effects and predicting survivorship. We propose a Bayesian semiparametric method for analyzing partly interval-censored data with areal spatial information under the proportional hazards model. A simulation study is conducted to compare the performance of the proposed method with the main method currently available in the literature and the traditional Cox proportional hazards model for right-censored data. The method is illustrated through a leukemia survival data set and a dental health data set. The proposed method will be especially useful for analyzing progression-free survival in multi-regional cancer clinical trials.
Keywords: partly interval-censored data, spatial frailty, proportional hazards model, conditionally autoregressive prior, Bayesian semiparametric
1. Introduction
Partly interval-censored data often occur in medical and epidemiological studies that include periodic examinations. With partly interval-censored data, the event times are exactly observed for some subjects, while only known to be within certain time intervals for the rest. It is a combination of exact event times and general interval-censored (Huang and Wellner 1997; Bogaerts, Komárek, and Lesaffre 2017, p.5) event times; or equivalently, a combination of exact, left-censored, interval-censored, and right-censored event times. For instance, in cancer clinical trials, progression-free survival, defined as time from study entry to disease progression or death due to any cause, is actually partly interval-censored. Also disease-free survival, defined as the length of time a patient stays free of a disease or cancer after a particular treatment, is also partly interval-censored. Some of the main methodological publications for partly interval-censored data are Huang (1999), Kim (2003), Komárek and Lesaffre (2007), Zhao et al. (2008), Gao, Zeng, and Lin (2017), and Zhou and Hanson (2018).
Depending on the type of geographic information available for each subject (geostatistical data vs. lattice data), the spatial dependency among them are commonly modeled in two ways: geostatistical models, when the exact geographic location (e.g. latitude and longitude) of the centroid of each area or of each subject is available; lattice models, when the adjacency of areas rather than any type of continuous distance metric is available (Banerjee, Wall, and Carlin 2003). For geostatistical data, the conventional model is a multivariate normal distribution whose variance-covariance matrix depends on the distances between locations through some function. For lattice data, which is the focus of this paper, the conventional model is the conditionally autoregressive (CAR) distribution which only uses the proximity information between areas, initially developed by Besag (1974). Some of the good references for CAR model are Besag (1974), Besag and Kooperberg (1995), Banerjee, Wall, and Carlin (2003), Carlin and Banerjee (2003), Hodges, Carlin, and Fan (2003), and Banerjee, Carlin, and Gelfand (2014).
Partly interval-censored data have been treated as right-censored data and analyzed with classic suvival analysis tools (e.g., Kaplan-Meier curve, log-rank test, and Cox proportional hazards model); and spatial dependency, if exists, is often ignored. Current literature for spatially correlated partly interval-censored data is very limited. The main method available is Zhou and Hanson (2018) who developed a unified approach that fits proportional hazards (PH), proportional odds, and accelerated failure time models to partly interval-censored and left-truncated spatial data. The R function that implements their method for partly interval-censored spatial data is survregbayes in the spBayesSurv package (Zhou, Hanson, and Zhang 2018).
The proposed method differs from Zhou and Hanson (2018) from the following perspectives: (1) The survregbayes function needs to obtain initial values either from its centering parametric frailty model by running an initial chain or from a parametric non-frailty model by the survreg function in the survival package (Therneau et al. 2020). While the proposed method does not rely on another function, but just simply sets noninformative initial values; (2) The survregbayes function performs standardization (subtracting sample mean and dividing by sample standard deviation) for all covariates together. While the proposed method allows one to choose which covariates to standardize so as to improve the Markov chain Monte Carlo (MCMC) mixing. This provides flexibility as standardizing a binary covariate does not quite make sense.
The remainder of the paper is outlined as follows. Section 2 describes the proposed method including spline approximation, data augmentation, CAR model, and posterior computation. Section 3 presents a simulation study that evaluates the performance of the proposed method and compares it with Zhou and Hanson (2018) and coxph in the survival package. In Section 4, we apply the proposed method, Zhou and Hanson (2018), and coxph to the spatial leukemia survival data contained in the spBayesSurv package and the spatial dental health data in the bayesSurv package (Komárek 2020). Finally Section 5 provides conclusions and discussions.
2. Statistical method
2.1. Data
Let there be i = 1, …, I spatial areas. In area i, suppose failure times are exactly known for the first ni1 subjects, denoted as Tij, j = 1, …, ni1. But failure times are only known to be within a time interval for the other ni − ni1 subjects, denoted as (Lij, Rij], j = ni1 + 1, …, ni. Here Lij can be 0 and Rij can be ∞. We assume that failure time and examination times are independent given covariates.
2.2. Model
The Cox proportional hazards model with spatial frailty for the jth subject in the ith area (denoted as subject [i, j]) is:
| (1) |
where λ0(·) is the baseline hazard function, β the p × 1 regression coefficient vector, xij the covariate vector, and ϕi the spatial frailty for area i.
For an exact observation, Tij is directly observed, and its likelihood function is
| (2) |
where Λ0(·) is the cumulative baseline hazard function.
For a general interval-censored observation, (Lij, Rij] is the observed time interval, and its likelihood function is
| (3) |
where F(·|x) is the cumulative distribution function given x and δ1, δ2, δ3 are the left-, interval-, and right-censoring indicators.
So the overall likelihood function is:
| (4) |
2.3. Estimation of Λ0(t) and λ0(t)
Given that the cumulative baseline hazard function Λ0(t) is non-negative and non-decreasing, we approximate it with a linear combination of a set of basis I-splines which are non-negative, non-decreasing, and range from 0 to 1 (Ramsay 1988). Specifically, we model Λ0(t) as
| (5) |
where {γl} is a set of non-negative coefficients and {Il(t)} is a set of basis I-splines. The number of basis I-splines (K) equals the degree of each basis spline (1 = linear, 2 = quadratic, 3 = cubic, etc.) plus the number of interior knots.
For the baseline hazard function λ0(t), since it is the derivative of Λ0(t), we model it as
| (6) |
where {Ml(t)} is a set of basis M-splines. We are able to do so because a basis I-spline is the integral of its corresponding basis M-spline by definition in Ramsay (1988), i.e., .
2.4. Data augmentation
It would be difficult to draw MCMC samples from the posteriors derived directly based on the observed data likelihood (4). To facilitate posterior computation, we construct the following data augmentations in order to obtain more posterior distributions of standard forms.
2.4.1. Data augmentation 1
For the general interval-censored observations part, suppose {N(t): t > 0} is a non-homogeneous Poisson process with cumulative intensity function Λ0(t)exp(β′x + ϕ). Then T = inf{t: N(t) > 0}, time of the first occurrence in the Poisson process, follows our model in (1). Define two time points t1 < t2 wherein for left-censoring, t1 = R; for interval-censoring, t1 = L and t2 = R; and for right-censoring, t2 = L. Then two latent variables Z = N(t1) and W = N(t2) − N(t1) are independent Poisson random variables. Furthermore, decompose Z and W respectively into K independent Poisson latent variables {Zl} and {Wl}. Then the augmented data likelihood for a general interval-censored subject [i, j] is as below. A similar but more detailed derivation can be found in Pan, Cai, and Wang (2020).
2.4.2. Data augmentation 2
For the exact observations part, introduce latent variables so as to convert in (6) to . This enables us to extract the portion involving γl directly in its posterior computation.
2.5. CAR model
For the spatial frailty ϕi, we assume a conditionally autoregressive (CAR) prior (Besag 1974):
| (7) |
where wij = 1 if areas i and j are neighbors, 0 otherwise, and is the number of neighbors of area i. τ is the spatial precision parameter.
Then by Brook’s Lemma (Brook 1964), the joint distribution of ϕ = (ϕ1, …, ϕI)′ is:
| (8) |
where W is the adjacency matrix with elements (W)ij = wij and Dw is a diagonal matrix with diagonals (Dw)ii = wi+.
Note that (Dw − W)1 = 0, so Dw − W is singular. Theoretically, the impropriety in (8) can be remedied by either adding a sum-to-zero constraint or replacing Dw − W with nonsingular Dw − ρW, where ρ ∈ (0, 1) (Gelfand and Vounatsou 2013; Banerjee, Carlin, and Gelfand 2014, p.81). However, a consequential spatial correlation still requires ρ to be close to 1 (Besag and Kooperberg 1995; Banerjee, Carlin, and Gelfand 2014, p.82), so normally we would employ the improper prior with the sum-to-zero constraint.
To include the spatial precision parameter τ in the Bayesian analysis, we need to multiple the kernel in (8) by τκ for some κ. Hodges, Carlin, and Fan (2003) derived where g is the number of disconnected groups of areas. The more complete prior for ϕ thus becomes . For a map where all areas are connected, we have g = 1.
2.6. Posterior computation
For spline coefficients, an Exponential prior γl ~ Exp(η) and a Gamma hyperprior η ~ Ga(aη, bη) are assumed. This leads to conjugate posteriors for both γl and η. For βr of a numeric covariate, a Normal prior is assumed. The corresponding posterior is not conjugate and the Metropolis-Hastings algorithm (Hastings 1970) is used for sampling from the posterior. For a categorical covariate with c levels, we denote it using c − 1 dummy variables and sample the exponentiated parameter ζr = exp(βr) for each dummy variable. A Gamma prior ζr ~ Ga(aζ, bζ) delivers a conjugate posterior. Then we transform ζr back to βr. For spatial frailties ϕi, the CAR prior in (7) is assumed. The posterior is not conjugate and the Metropolis-Hastings algorithm is used. For spatial precision parameter, a Gamma prior τ ~ Ga(aτ, bτ) with mean and variance also leads to a conjugate posterior.
For detailed posterior formulations, please refer to Appendix.
3. A simulation study
We evaluate the performance of the proposed method through a simulation study. We fit the proposed method, Zhou and Hanson (2018) method with the survregbayes function in the spBayesSurv package, and the traditional Cox PH model for right-censored data with the coxph function in the survival package. For coxph, we convert the partly interval-censored data to right-censored data as conventionally done by practitioners, i.e. take right endpoints of finite time intervals (left-censored and interval-censored observations) as the observed event times. The purpose is to see how the conventional approach can introduce bias in the estimation of fixed effects and survival function.
A total of 100 data sets are generated. The spatial layout is based on the 46 counties in South Carolina, with ni = 20 subjects within each county. For each data set, failure times are generated from a PH model with spatial frailty:
where Λ0(t) = log(1 + t), β1 = β2 = 1, xij1’s ~ Bernoulli(0.5), and xij2’s ~ N(0, 0.52). The spatial precision parameter τ is set to be 4. The number of medical examinations performed for each person is generated from Poi(2) + 1. The gap times between adjacent examinations are generated from Exp(1). The observed intervals are the ones that contain the true failure times. In each data set, there are N = 920 subjects, around 20% of which are set to have exact event times observed.
We set the degree of basis I-splines as 2 and choose knots = (0, 2, 6, max(L, R, T)+1), where L, R, and T are observed timepoints. For hyperparameters, we set , aη = bη = 1, aζ = bζ = 1, and aτ = bτ = 0.1. Fast convergence and good mixing were observed for all key parameters. For fair comparison, we set aτ = bτ = 0.1 in survregbayes too. Other hyperparameters in survregbayes are set to their default values. For each MCMC chain of both methods, we set total number of iterations = 6,000, burn-in = 1,000, and thin = 1.
Table 1 summarizes the simulation results. For each parameter, the point estimate is the average of the 100 posterior means, SSD is the sample standard deviation of the 100 posterior means, ESE is the average of the 100 empirical standard errors, 95CP is the coverage probability of the 100 95% credible intervals, and ESS is the effective sample size computed using the coda package (Plummer et al. 2019). Two model selection criteria are considered: log psuedo marginal likelihood (LPML) (Geisser and Eddy 1979; Dey, Chen, and Chang 1997) and deviance information criterion (DIC) (Spiegelhalter et al. 2002, 2014). LPML is the sum of log conditional predictive ordinates and measures model cross-validation predictive performance and DIC equals posterior mean of deviance plus model effective number of parameters. Smaller absolute values of LPML and DIC indicate better model fit.
Table 1:
Simulation - Estimation of regression coefficients, ESS, LPML, and DIC based on the proposed method, survregbayes, and coxph.
| R function | True | Estimate | SSD | ESE | 95CP | ESS | LPML | DIC |
|---|---|---|---|---|---|---|---|---|
| Proposed method | β1 = 1 | 1.021 | 0.088 | 0.094 | 0.97 | 254 | −683 | 1364 |
| β2 = 1 | 1.020 | 0.087 | 0.090 | 0.96 | 380 | |||
| τ = 4 | 4.733 | 2.515 | 2.550 | 0.95 | 161 | |||
| survregbayes | β1 = 1 | 1.014 | 0.089 | 0.094 | 0.96 | 427 | −682 | 1362 |
| β2 = 1 | 1.018 | 0.091 | 0.089 | 0.94 | 208 | |||
| τ = 4 | 4.862 | 2.376 | 2.591 | 0.98 | 266 | |||
| coxph | β1 = 1 | 0.636 | 0.065 | 0.076 | 0.00 | −4068 | ||
| β2 = 1 | 0.672 | 0.074 | 0.078 | 0.01 |
As seen in Table 1, both the proposed method and survregbayes provide very good estimation for the regression coefficients, with small bias, sample standard deviation close to empirical standard error, and coverage probability close to nominal level. The overall model goodness-of-fits are similar too as indicated by the model selection criteria: LPML and DIC. The coxph function performs badly with large bias, coverage probability close to 0, and very small log-likelihood.
Figure 1 presents the true baseline survival function S0(t) versus the ones estimated using the proposed method, survregbayes, and coxph, averaged over the 100 simulated data sets. Both the proposed method and survregbayes provide very close approximations. However, the one from coxph differs from the true curve significantly.
Figure 1:
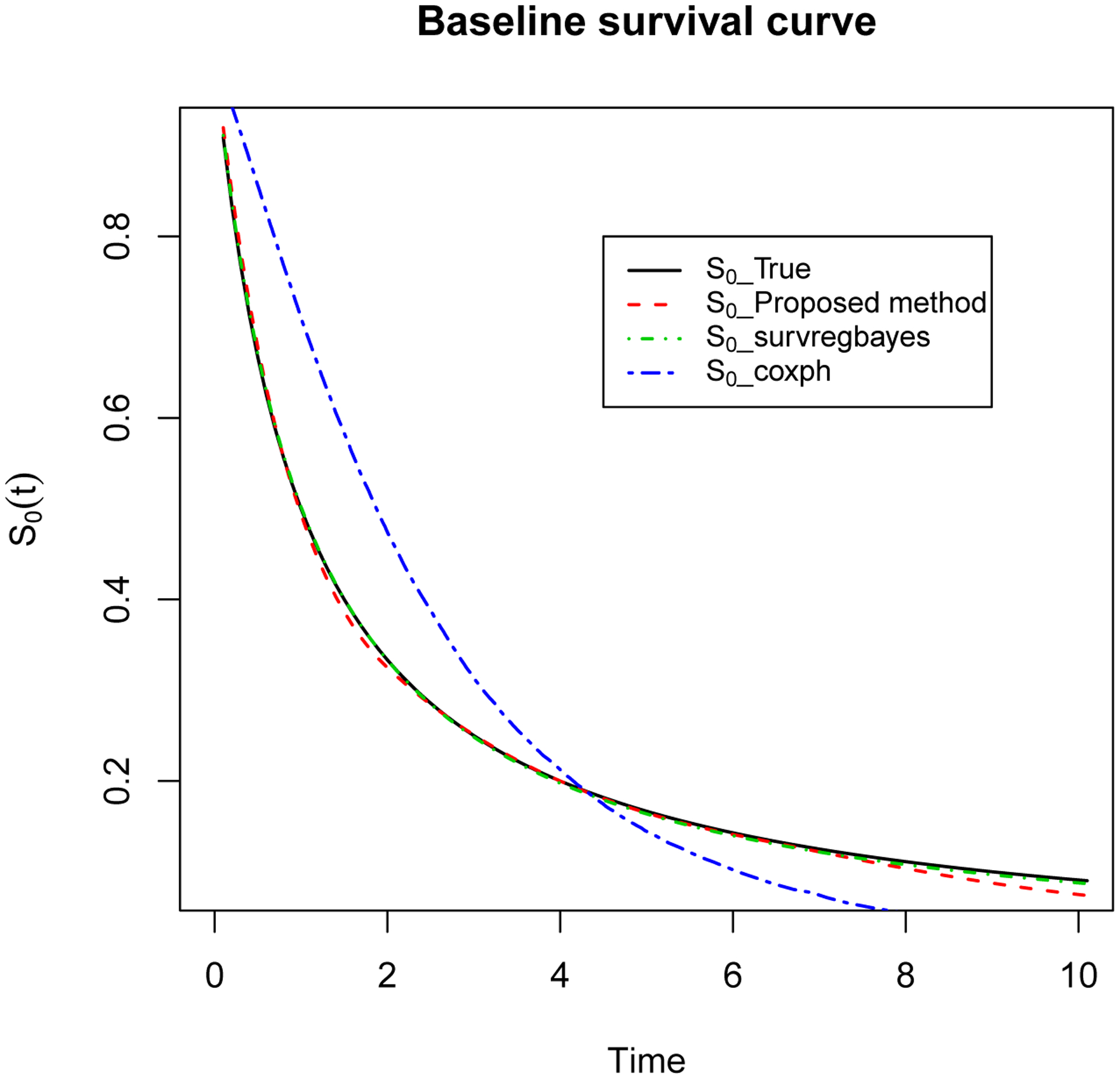
Simulation - Plot of estimated S0(t) based on 100 simulated data sets using the proposed method, survregbayes, and coxph, compared to true S0(t) curve.
To study the sensitivity of the model to the prior of τ, we further try the other two more informative priors: Ga(1, 1) and Ga(4, 4). The prior mean is kept as 1 but the prior variance decreases from 10 to 1 and 0.25 respectively. We find that the estimation for regression coefficients, baseline survival, and model fitting criteria remain virtually the same. However, the point estimate, sample standard deviation, empirical standard error, and coverage probability for τ itself change greatly. Especially, the coverage probability decreases from 0.95 to 0.81 for Ga(1, 1) and 0 for Ga(4, 4). This observation also holds true for the survregbayes function. The potential reason might be that Gamma priors are hyperpriors for τ, resulting in that τ updates do not directly use the data information. The sensitivity analysis confirms the robustness of the proposed method and informs our recommendation of using a noninformative prior for τ. Similarly, Hodges, Carlin, and Fan (2003) also tried priors τ ~ Ga(0.001, 0.001) and Ga(0.1, 0.1) for a periodontal data and noticed great differences in the estimation for τ. It is also of interest to note that Banerjee, Carlin, and Gelfand (2014, p.82) have pointed out that the magnitude of τ should not be viewed as quantifying the strength of spatial association. The reason is that if all ϕi’s are multiplied by a constant a, then τ becomes but the strength of spatial association stays the same.
4. Leukemia survival data
We apply the proposed method, survregbayes, and coxph to a data set maintained by the North West Leukemia Register in the UK on the survival of N = 1,043 acute myeloid leukemia patients where patients’ district information is available (Henderson, Shimakura, and Gorst 2002). The purpose of the analysis is to examine possible spatial variation in survival after accounting for known subject-specific prognostic factors. The data set contains observed survival time, censoring indicator, and four covariates: age, white blood cell count at diagnosis (wbc), Townsend deprivation index (tdi) for which higher values indicate more deprived areas, and sex (0 = F, 1 = M). The data set is actually right-censored with around 16% cases censored. There are 24 administrative districts.
Table 2 presents the estimation results. We choose the degree of basis I-splines as 2 and knots = (0, 1000, 3000, 5000). The hyperparameter values are the same as in the simulation study. We standardize the continuous covariates age, wbc, and tdi for the proposed method as it noticeably improves MCMC mixing. The regression coefficient estimation results from all three methods are quite similar. We can see that age, wbc, and tdi all have significant effects on survival in patients. The proposed method has higher ESS for regression coefficients and lower ESS for spatial precision parameter, compared to survregbayes. This is because the auto-correlation in the MCMC chains has been reduced and hence the efficiency of MCMC sampling improved after standardization.
Table 2:
Acute myeloid leukemia data - Estimation of regression coefficients, ESS, LPML, and DIC based on the proposed method, survregbayes, and coxph.
| R function | Estimate | SE | 95% CI | ESS | LPML | DIC | |
|---|---|---|---|---|---|---|---|
| Proposed method | age | 0.0349 | 0.0022 | (0.0306, 0.0394) | 808 | −6020 | 12030 |
| wbc | 0.0035 | 0.0005 | (0.0025, 0.0043) | 752 | |||
| tpi | 0.0342 | 0.0103 | (0.0140, 0.0544) | 454 | |||
| sex | 0.0718 | 0.0704 | (−0.0670, 0.2096) | 1460 | |||
| τ | 7.7090 | 4.1733 | (2.5611, 17.9981) | 368 | |||
| survregbayes | age | 0.0315 | 0.0021 | (0.0274, 0.0357) | 343 | −5945 | 11886 |
| wbc | 0.0031 | 0.0005 | (0.0023, 0.0040) | 300 | |||
| tpi | 0.0297 | 0.0091 | (0.0125, 0.0477) | 365 | |||
| sex | 0.0680 | 0.0674 | (−0.0726, 0.1949) | 311 | |||
| τ | 10.3457 | 5.7867 | (3.2822, 25.4528) | 539 | |||
| coxph | age | 0.0296 | 0.0021 | (0.0255, 0.0338) | −5326 | ||
| wbc | 0.0031 | 0.0004 | (0.0022, 0.0039) | ||||
| tpi | 0.0293 | 0.0090 | (0.0116, 0.0470) | ||||
| sex | 0.0522 | 0.0678 | (−0.0807, 0.1850) |
We also estimate the survival functions for female patients with wbc = 38.59, tdi = 0.3398, and age = 49, 65, and 74 as in Zhou, Hanson, and Zhang (2020). As seen in Figure 2, the three methods result in similar estimated survival curves for all of the three age groups.
Figure 2:
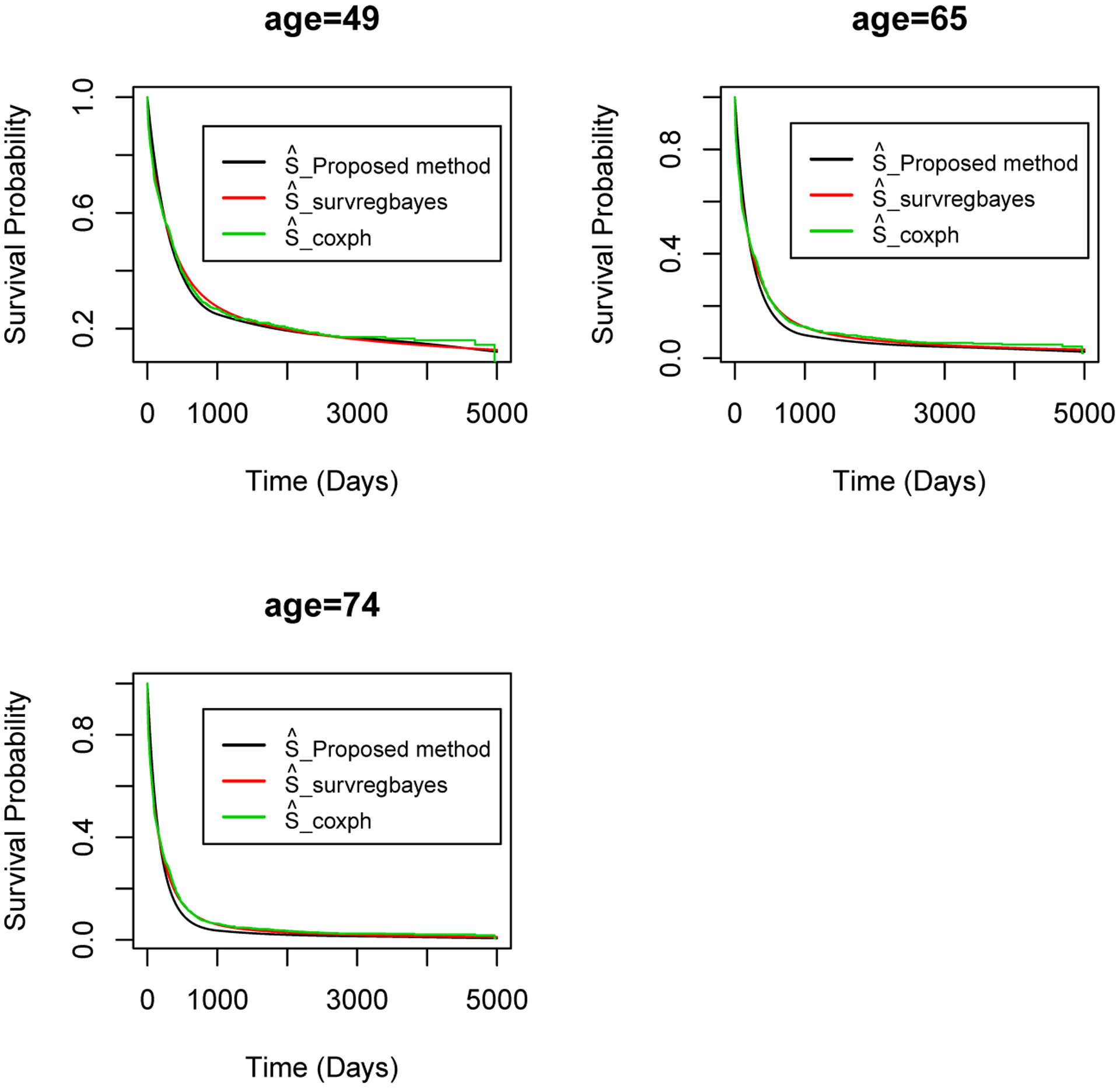
Acute myeloid leukemia data - Estimated survival curves using the proposed method, survregbayes, and coxph for female patients with wbc = 38.59, tdi = 0.3398, and age = 49, 65, 74.
To explore the residual spatial pattern, the posterior means of spatial frailty ϕi’s for the 24 districts from the proposed method and survregbayes are mapped (Figure 3). The spatial patterns detected by the two methods are the same. There are noticeable spatial patterns after accounting for the diagnostic factors age, wbc, tdi, and sex. For instance, the top north district shows a higher than average risk of dying from the disease, and the six districts below it show lower than average risks.
Figure 3:
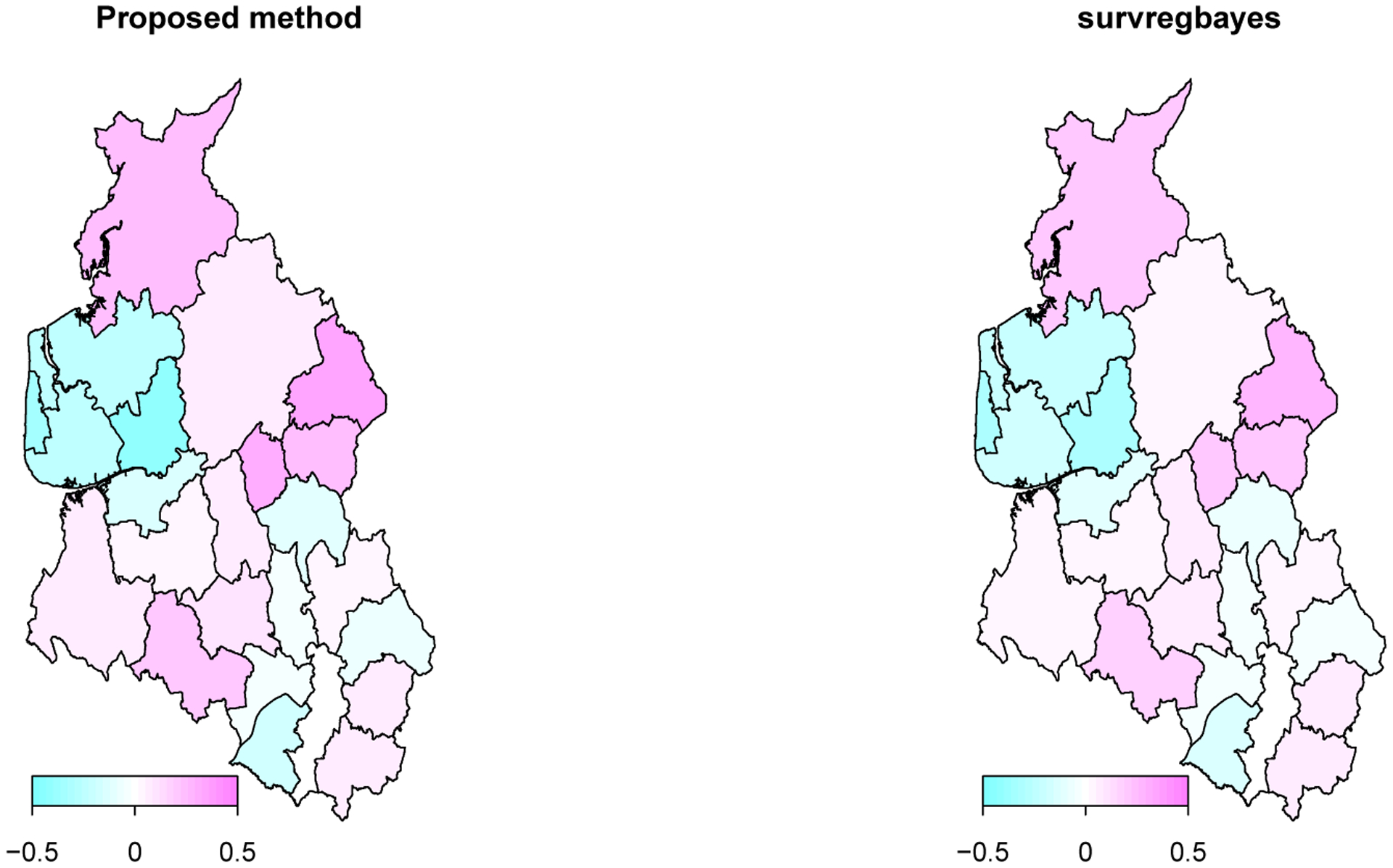
Maps of the posterior means of spatial frailty ϕi’s over the 24 districts in north west UK based on the proposed method and survregbayes.
For this data, coxph performs well for both fixed effects estimation and survival curve estimation, the reason is because the data itself is right-censored and we suspect the spatial variation is less strong here as the districts are small local authority units. This similarity in results on the other hand verifies that the proposed method and survregbayes perform well for right-censored data, even though they are designed for spatial partly interval-censored data.
As in the simulation study, besides Ga(0.1, 0.1), we try the other two priors for τ: Ga(1, 1) and Ga(4, 4), and observe the same phenomenon. The estimation for fixed effects, survival curves, and LPML and DIC are unaffected while the estimation for τ varies significantly with the prior. For example, the point estimate for τ changes from 7.71 for Ga(0.1, 0.1) to 3.86 for Ga(1, 1) and 2.17 for Ga(4, 4).
5. Dental health data
The Signal Tandmobiel study is a longitudinal dental study conducted in North Belgium on 4, 468 first-year school children born in 1989. Each child was examined annually by one of 16 trained dentists from age 7 to age 12 (i.e. from year 1996 to year 2001). The tandmob2 data set in the bayesSurv package contains interval-censored emergence time and caries time of each permanent tooth, some baseline covariates, and residential provinces for N = 4,430 children of the study (38 sampled children did not come to any of the designed dental examinations). We pick Tooth 16 (the permanent first molar in the upper right quadrant) and investigate how its caries time (T = age when caries appear) can be affected by STARTBR (the starting age of teeth brushing) and T55.DMF (1 if Tooth 55 was decayed or missing due to caries or filled, 0 if not). Tooth 55 is the deciduous second molar in the upper right quadrant. It sheds around age 10–12 and Tooth 16 emerges next to Tooth 55 around age 6–7. We include Tooth 55 to see if a permanent first molar’s condition would be affected by the deciduous molar next to it. Since the data set contains the five provinces in North Belgium: Antwerpen, Limburg, Oost-Vlaanderen, Vlaams Brabant, and West-Vlaanderen, we are able to treat the children as clustered by their residential provinces.
We fit the proposed model, survregbayes, and coxph (Table 3). The estimation results for the fixed effects are similar. Both starting age of teeth brushing and condition of Tooth 55 significantly affect the caries time of the permanent first molar Tooth 16. Interestingly, the log-likelihood from coxph is much smaller. This indicates the existence of spatial pattern, and the inclusion of spatial frailty has improved model fitting by accounting for a significant amount of unexplained variation in the failure time.
Table 3:
Signal Tandmobiel data - Estimation of regression coefficients, ESS, LPML, and DIC based on the proposed method, survregbayes, and coxph.
| R function | Estimate | SE | 95% CI | ESS | LPML | DIC | |
|---|---|---|---|---|---|---|---|
| Proposed method | STARTBR | 0.1109 | 0.0326 | (0.0473, 0.1741) | 112 | −3375 | 6751 |
| T55.DMF | 1.0128 | 0.0745 | (0.8685, 1.1602) | 870 | |||
| τ | 11.5778 | 8.4667 | (1.3079, 32.7055) | 2944 | |||
| survregbayes | STARTBR | 0.1243 | 0.0286 | (0.0655, 0.1776) | 70 | −3382 | 6763 |
| T55.DMF | 1.0490 | 0.0713 | (0.9155, 1.1992) | 272 | |||
| τ | 11.6408 | 8.8068 | (1.3688, 34.8549) | 4565 | |||
| coxph | STARTBR | 0.1179 | 0.0295 | (0.0601, 0.1756) | −6990 | ||
| T55.DMF | 1.0504 | 0.0722 | (0.9088, 1.1919) |
Figure 4 presents the survival curves for children who start brushing at age 4 and without caries in Tooth 55 versus with caries. We can see that a permanent first molar can have caries as early as around age 6–7, i.e. right after it erupts. If next to a decayed primary molar, Tooth 16 is obviously more likely to have caries. Also the estimated survival curves from coxph are somewhat different from the curves estimated by the proposed method and survregbayes.
Figure 4:
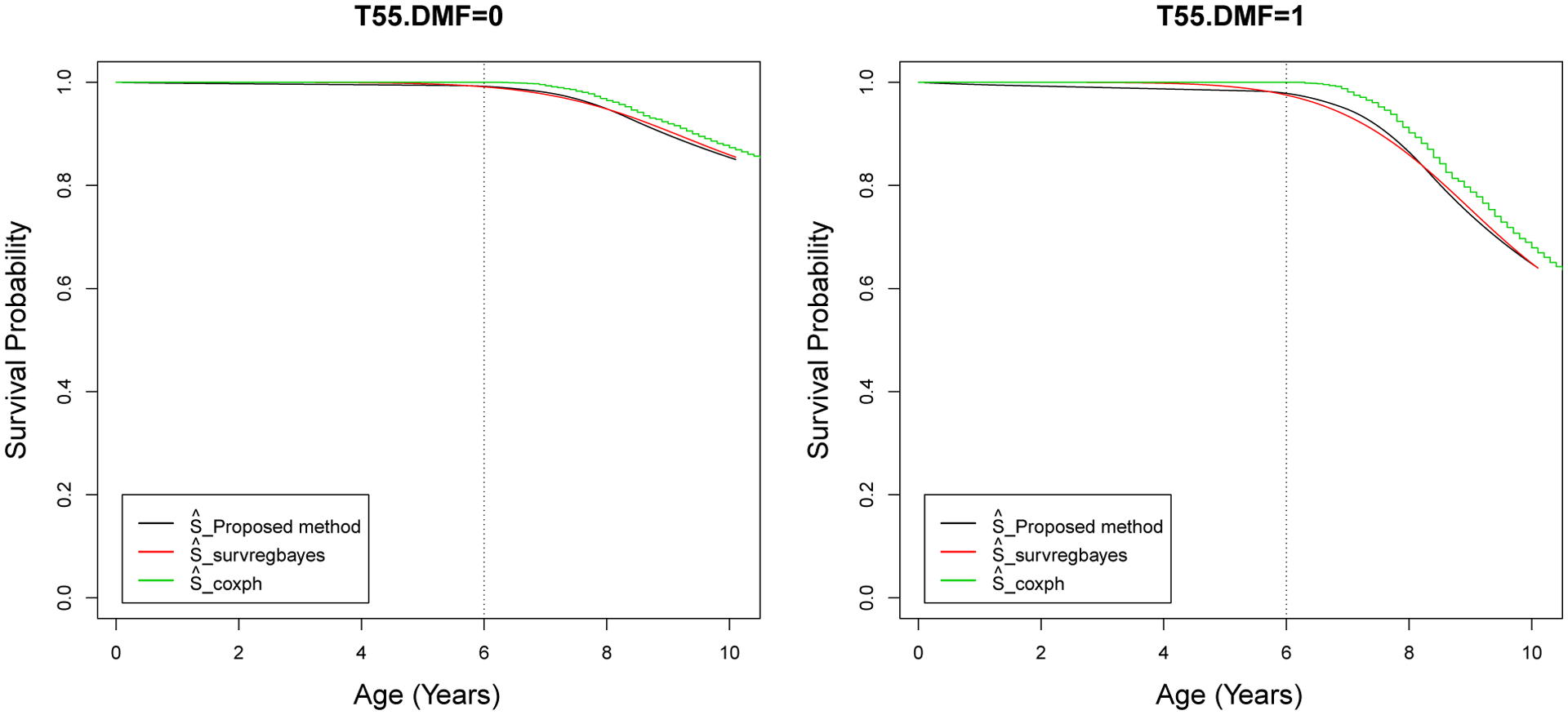
Signal Tandmobiel data - Estimated survival curves using the proposed method, survregbayes, and coxph for children with STARTBR = 4 and T55.DMF = 0, 1.
The estimated spatial frailty ϕi’s from the proposed method and survregbayes are plotted in Figure 5. The two methods detect the same spatial patterns. As we can see, children in Limburg have a significantly higher risk of cavities while children in West-Vlaanderen have a significantly lower risk, given the same teeth brushing age and primary second molar condition.
Figure 5:
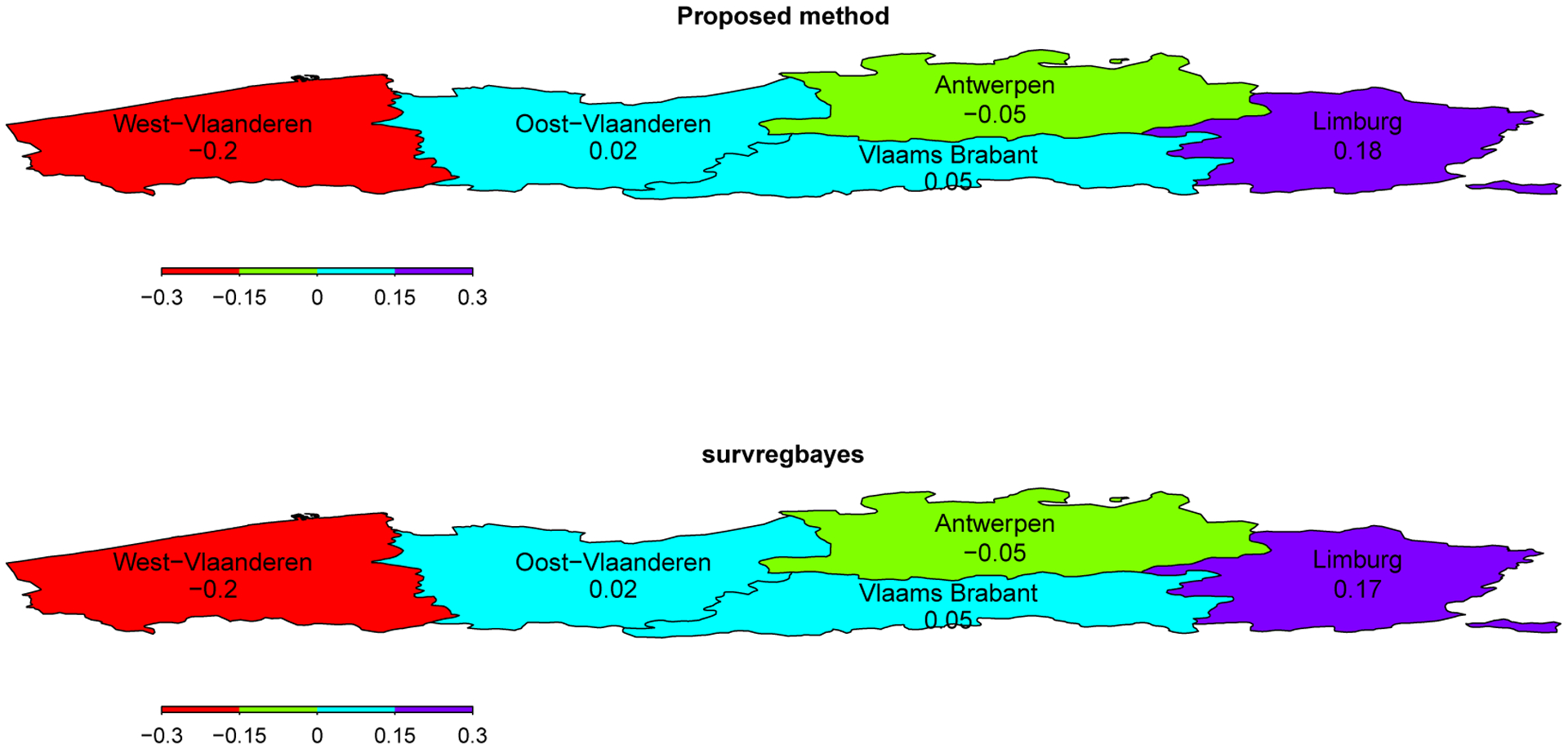
Maps of the posterior means of spatial frailty ϕi’s over the five provinces in North Belgium based on the proposed method and survregbayes.
Again we try different priors for τ: Ga(0.1, 0.1), Ga(1, 1) and Ga(4, 4). The corresponding point estimates for τ are 11.64, 2.66, and 1.46, while the estimation for fix effects, survival curves, and LPML and DIC do not change.
6. Conclusions
There has been exciting development for survival models with spatial frailty which mainly focused on right-censored data and later with additions for general interval-censored data during the past 20 years. Partly interval-censored data have received limited attention, even though they occur as often as general interval-censored data, for instance, progression-free survival and disease-free survival which are important endpoints in clinical trials. There might be unexplained heterogeneity in the data, after accounting for certain risk factors (fixed effects). With geographic information recorded for patients/subjects, the inclusion of spatial frailty can (1) improve model fitting by acting as a surrogate of unmeasured characteristics that vary by region (e.g. socioeconomic status, health care quality, environmental exposure); (2) improve the precision of inference for fixed effects by reducing random error; (3) identify spatial pattern that can inform us of differences in clinical practice among medical centers or inform further epidemiological studies.
Our simulation and real data analysis show that the proposed method performs comparably well as Zhou and Hanson (2018) for the fixed effects and survival curve estimation. Both methods significantly outperform the conventional approach when the data are partly interval-censored and with spatial dependency. This gives us the motivation to consider these new methods when analyzing progression-free survival from cancer clinical trials which are commonly conducted in multiple regions (e.g., states, nations). The inclusion of spatial frailty is especially important when the regions differ greatly while there are no predictors in the data to account for such differences.
Acknowledgment
We thank Dr. Emmanuel Lesaffre and Dr. Dominique Declerck for allowing us to use the Signal Tandmobiel data and reviewing the analysis result. We also greatly appreciate the Editor-in-Chief for his suggestion of investigating the sensitivity of the proposed method to the prior specification of the spatial precision parameter, which helped improve the manuscript.
Funding
The first author’s work was supported by the National Institute of Health under Award Number SC2GM135078.
Appendix
After initializing values for the parameters, the proposed MCMC algorithm proceeds in the following steps.
-
Let Zij = 0 and Wij = 0 for all i and j, Zijl = 0 and Wijl = 0 for all i, j, and l. If δ1ij = 1, then sampleIf δ2ij = 1, then sample
Sample (uij1, …, uijK) ~ Multinomial(1; γ1M1(tij), …, γKMK(tij)).
- For βr corresponding to a numeric covariate, use the Metropolis-Hastings algorithm to sample from its full conditional distribution
-
For βr corresponding to a binary covariate, let ζr = exp(βr), sample ζr from
where β−r = {βk : k ≠ r} and xij,−r = {xijk : k ≠ r}.
- Sample γl, l = 1, …, K, from
Sample η from .
- Sample ϕi, i = 1, …, I, using the Metropolis-Hastings algorithm from its full conditional distribution
Sample τ from .
References
- Banerjee S, Carlin BP, and Gelfand AE. 2014. Hierarchical modeling and analysis for spatial data. 2nd ed. Boca Raton, FL: Chapman Hall/CRC. [Google Scholar]
- Banerjee S, Wall M, and Carlin BP. 2003. Frailty modeling for spatially correlated survival data, with application to Q1 infant mortality in Minnesota. Biostatistics 4 (1): 123–42. doi: 10.1093/biostatistics/4.1.123. [DOI] [PubMed] [Google Scholar]
- Besag J 1974. Spatial interaction and the statistical analysis of lattice systems (with discussion). Journal of the Royal Statistical Society. Series B (Methodological) 36 (2): 192–236. [Google Scholar]
- Besag J, and Kooperberg C. 1995. On conditional and intrinsic autoregression. Biometrika 82 (4): 733–46. doi: 10.2307/2337341. [DOI] [Google Scholar]
- Bogaerts K, Komárek A, and Lesaffre E. 2017. Survival analysis with interval-censored data: A practical approach with examples in R, SAS, and BUGS. 1st ed. Boca Raton, FL: Chapman Hall/CRC. [Google Scholar]
- Brook D 1964. On the distinction between the conditional probability and the joint probability approaches in the specification of nearest-neighbour systems. Biometrika 51 (3/4): 481–3. [Google Scholar]
- Carlin BP, and Banerjee S. 2003. Hierarchical multivariate CAR models for spatio-temporally correlated survival data (with discussion). In Bayesian Statistics 7, edited by Bernardo JM, Bayarri MJ, Berger JO, Dawid AP, Heckerman D, Smith AFM, and West M, 45–63. Oxford: Oxford University Press. [Google Scholar]
- Dey DK, Chen M-H, and Chang H. 1997. Bayesian approach for nonlinear random effects models. Biometrics, 53 (4), 1239–52. doi: 10.2307/2533493. [DOI] [Google Scholar]
- Gao F, Zeng D, and Lin DY. 2017. Semiparametric estimation of the accelerated failure time model with partly interval-censored data. Biometrics 73 (4): 1161–8. doi: 10.1111/biom.12700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geisser S and Eddy WF. 1979. A predictive approach to model selection. Journal of the American Statistical Association, 74 (365), 153–160. doi: 10.2307/2286745. [DOI] [Google Scholar]
- Gelfand AE, and Vounatsou P. 2003. Proper multivariate conditional autoregressive models for spatial data analysis. Biostatistics 4 (1): 11–25. doi: 10.1093/biostatistics/4.1.11. [DOI] [PubMed] [Google Scholar]
- Hastings WK 1970. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57 (1): 97–109. doi: 10.2307/2334940. [DOI] [Google Scholar]
- Henderson R, Shimakura S, and Gorst D. 2002. Modeling spatial variation in leukemia survival data. Journal of the American Statistical Association 97 (460): 965–72. doi: 10.1198/016214502388618753. [DOI] [Google Scholar]
- Hodges JS, Carlin BP, and Fan Q. 2003. On the precision of the conditionally autoregressive prior in spatial models. Biometrics 59 (2): 317–22. doi: 10.1111/1541-0420.00038. [DOI] [PubMed] [Google Scholar]
- Huang J 1999. Asymptotic properties of nonparametric estimation based on partly interval-censored data. Statistica Sinica 9 (2): 501–19. [Google Scholar]
- Huang J, and Wellner JA. 1997. Interval censored survival data: A review of recent progress. In Proceedings of the First Seattle Symposium in Biostatistics, edited by Lin DY and Fleming TR, 123–69. New York: Springer. [Google Scholar]
- Kim JS 2003. Maximum likelihood estimation for the proportional hazards model with partly interval-censored data. Journal of the Royal Statistical Society: Series B (Methodological) 65 (2): 489–502. doi: 10.1111/1467-9868.00398. [DOI] [Google Scholar]
- Komárek A, and Lesaffre E. 2007. Bayesian accelerated failure time model for correlated interval-censored data with a normal mixture as an error distribution. Statistica Sinica 17 (2): 549–69. [Google Scholar]
- Komárek A 2020. bayesSurv: Bayesian survival regression with flexible error and random effects distributions. https://cran.r-project.org/package=bayesSurv. R package version 3.3.
- Pan C, Cai B, and Wang L. 2020. A Bayesian approach for analyzing partly interval-censored data under the proportional hazards model. Statistical Methods in Medical Research 29 (11): 3192–204. doi: 10.1177/0962280220921552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plummer M, Best N, Cowles K, Vines K, Sarkar D, Bates D, Almond R, and Magnusson A. 2019. coda: Output analysis and diagnostics for MCMC. https://cran.r-project.org/package=coda. R package version 0.19–3.
- Ramsay JO 1988. Monotone regression splines in action. Statistical Science 3 (4): 425–41. [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, and van der Linde A. 2002. Bayesian measures of model complexity and fit (with discussion). Journal of the Royal Statistical Society: Series B (Methodological) 64 (4): 583–679. doi: 10.1111/1467-9868.00353. [DOI] [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, and van der Linde A. 2014. The deviance information criterion: 12 years on. Journal of the Royal Statistical Society. Series B (Methodological) 76 (3): 458–93. doi: 10.1111/rssb.12062. [DOI] [Google Scholar]
- Therneau TM, Lumley T, Elizabeth A, and Cynthia C. 2020. survival: Survival Analysis. https://cran.r-project.org/package=survival. R package version 3.2–7.
- Zhao X, Zhao Q, Sun J, and Kim JS. 2008. Generalized log-rank tests for partly interval-censored failure time data. Biometrical Journal. 50 (3): 375–85. doi: 10.1002/bimj.200710419. [DOI] [PubMed] [Google Scholar]
- Zhou H, and Hanson T. 2018. A unified framework for fitting Bayesian semiparametric models to arbitrarily censored survival data, including spatially-referenced data. Journal of American Statistical Association 113 (522): 571–81. doi: 10.1080/01621459.2017.1356316. [DOI] [Google Scholar]
- Zhou H, Hanson T, and Zhang J. 2020. spBayesSurv: Fitting Bayesian spatial survival models using R. Journal of Statistical Software 92 (9): 1–33. doi: 10.18637/jss.v092.i09. [DOI] [Google Scholar]
- Zhou H, Hanson T, and Zhang J. 2018. spBayesSurv: Bayesian modeling and analysis of spatially correlated survival data. https://cran.r-project.org/package=spBayesSurv. R package version 1.1.3.


