Abstract
Individualized treatment rules (ITRs) recommend treatments that are tailored specifically according to each patient’s own characteristics. It can be challenging to estimate optimal ITRs when there are many features, especially when these features have arisen from multiple data domains (e.g., demographics, clinical measurements, neuroimaging modalities). Considering data from complementary domains and using multiple similarity measures to capture the potential complex relationship between features and treatment can potentially improve the accuracy of assigning treatments. Outcome weighted learning (OWL) methods that are based on support vector machines using a predetermined single kernel function have previously been developed to estimate optimal ITRs. In this paper, we propose an approach to estimate optimal ITRs by exploiting multiple kernel functions to describe the similarity of features between subjects both within and across data domains within the OWL framework, as opposed to preselecting a single kernel function to be used for all features for all domains. Our method takes into account the heterogeneity of each data domain and combines multiple data domains optimally. Our learning process estimates optimal ITRs and also identifies the data domains that are most important for determining ITRs. This approach can thus be used to prioritize the collection of data from multiple domains, potentially reducing cost without sacrificing accuracy. The comparative advantage of our method is demonstrated by simulation studies and by an application to a randomized clinical trial for major depressive disorder that collected features from multiple data domains. Supplemental materials for this article are available online.
Keywords: Multiple Kernel Learning, Precision Medicine
1. Introduction
When making a treatment decision for an individual patient, it is crucial to assign the treatment that is most likely to be most effective specifically for each patient. Patients manifest heterogeneous response to treatments and tailoring clinical decisions to patients’ individual characteristics, rather than a “one size fits all” approach, is termed precision medicine. Precision medicine can be aided by recent technology advances that provide accessibility to comprehensive data domains of patients’ characteristics such as clinical evaluations, neuroimaging measurements, genomics data, and mobile health data. Improvements in making precise treatment decisions for complex diseases can be achieved by exploiting these data appropriately.
Several methods have been developed to estimate an individualized treatment rule (ITR) for precision medicine that depend on each individual’s characteristics. A popular approach to estimating ITR’s is to use regression-based methods. For example, Q-learning is meant to estimate the mean of clinical outcomes, conditional on an individual’s prognostic variables and treatment received, and then determine the ITR by maximizing the predicted conditional mean (Qian and Murphy, 2011; Zhang et al., 2012b; Kang et al., 2014). An alternative general approach to estimating ITRs is classification-based, i.e., directly maximizing the marginal mean of the outcome by solving a classification problem (Zhang et al., 2012a; Zhao et al., 2012). Outcome weighted learning (OWL; Zhao et al., 2012) solves the classification problem with outcomes serving as weights by implementing a kernel-based support vector machine (SVM) (Hastie et al., 2009). The kernel function in OWL is used to measure the similarity between the features of each pair of subjects. Augmented outcome-weighted learning (AOL; Liu et al., 2018) improves OWL by allowing negative outcome weights and reducing the variability of outcome weights in order to achieve higher accuracy. These state of the art classification-based methodologies model the association between a treatment and an individual subject’s features by using a pre-determined single kernel function. This approach is limited in that it can be inefficient when a kernel is not optimally specified or when the association between treatment and subject characteristics is too complex to be measured using only a single kernel.
In many precision medicine scenarios, the available data for each subject are quite complex, perhaps including data that are gathered from each of several domains (e.g., genomics, neuroimaging, clinical, behavioral, etc.). In such a situation, a classification-based approach that relies on a single kernel to account for the relationship between the baseline data and the treatment will likely not be adequate to provide optimal treatment decisions. Multiple kernel learning (MKL) has been extensively used in classification problems (Bach et al., 2004; Lanckriet et al., 2004a; Bach, 2008; Rakotomamonjy et al., 2008; Gönen and Alpayd in, 2011). It has been successfully applied to problems such as protein functional classifications using multiple types of data (Lanckriet et al., 2004c) and classifying proteins based on various types of genome-wide measurements (Lanckriet et al., 2004b). To date, however, this powerful approach has yet to be explored in the realm of precision medicine to develop ITRs.
Several recent works have estimated ITRs from multiple data sources (Shi et al., 2018; Wu et al., 2020). However, those works consider data sources from multiple studies with different subjects, such as studies conducted at multiple centers (Shi et al., 2018), a randomized clinical trial and an observational study (Wu et al., 2020). In contrast, we are interested in subjects from a single study, but their measurements are collected across multiple domains (e.g., neuroimaging, clinical, etc.).
In this paper, we propose a novel method for estimating ITRs within the MKL framework. We use multiple kernel functions to allow a variety of similarity relationships between pairs of subjects. Data domain knowledge may be incorporated in order to group variables from the same data domain (those that might be expected to be more biologically similar) by using separate kernels for each data domain.
2. Methods
We begin by reviewing OWL and AOL, approaches that are based on the choice of a single kernel. Subsequently, we will describe an approach for using multiple kernels to estimate ITRs.
2.1. Outcome Weighted Learning (OWL)
We consider a single stage two-arm clinical trial. Let A denote the treatment assignment variable: A ∈ 𝒜 = {−1, 1}. Let Y denote the observed clinical outcome (where we assume larger values are more beneficial). Let x ∈ 𝒳 denote a subject’s characteristics measured at baseline. The ITR 𝒟 maps X to A. The marginal mean of an observed outcome under an ITR 𝒟 is referred to as the value function and is defined as (Qian and Murphy, 2011), where π(A) is the treatment assignment probability (which would typically be known in a randomized clinical trial and could potentially be estimated for an observational study). π(A) could depend on X in some cases. Here, we ignore X in notations. The optimal treatment rule 𝒟* is a rule that maximizes 𝒱(𝒟) over choices of 𝒟. Maximizing 𝒱(𝒟) is equivalent to minimizing over 𝒟.
Suppose that we observe independent and identically distributed (i.i.d.) data (Xi, Ai, Yi), i = 1, …, n. The optimal rule 𝒟* can be estimated by minimizing . Since 𝒟(Xi) can always be represented by sign (f(Xi)) for some decision function f ∈ ℋ, e.g., ℋ is a reproducing kernel Hilbert space (RKHS, Berlinet and Thomas-Agnan, 2011), this criterion is equivalent to minimizing
| (1) |
over f (Hastie et al., 2009, Chapter 5). Let f* be the optimal f, then the optimal treatment rule 𝒟* = sign (f*(Xi)). OWL (Zhao et al., 2012) estimates the optimal treatment rule by replacing the 0–1 loss in (1) by a hinge loss and solving a weighted classification problem with a penalty on f:
| (2) |
where [x]+ = max(x, 0), and ∥·∥ is a norm defined in a metric space. When the decision function is a linear function of X, then f(X) = ωTX + β0 with ∥ f ∥2 defined as ωTω. This linear decision function may not perform well when the optimal decision depends on a complex relationship between treatments and data. As an alternative, a nonlinear decision function f can be used and represented by , where k : 𝒳 × 𝒳 → ℛ is a positive definite kernel function, and the corresponding space of functions ℋ is a RKHS. Common choices of kernel functions include the linear kernel, the Gaussian kernel, and polynomial kernels. The norm of f in ℋ is induced by inner product, and , where K is a n × n matrix of k (Xi, Xj) for all pairs (i, j) and ω = (ω1, …, ωn)T (Berlinet and Thomas-Agnan, 2011, Chapter 1).
AOL (Liu et al., 2018) replaces Yi in (2) by the residual Ri obtained by regressing out the main effects in order to reduce the variability in outcome. The AOL objective minimizes
| (3) |
over f, where Aisign(Ri) is the class label and is the outcome weight. In the spirit of the SVM approach (e.g., Hastie et al., 2009, Chapter 12) that solves a classification problem by finding the decision hyperplane f(X) = 0 that best separates the sample points for class 1 and −1 while allowing for some tolerable overlap, the weighted classification problem (3) can be rewritten in the primal form of the SVM problem by introducing a slack variable ξi which represents the tolerance of misclassification. This leads to solving the following optimization problem:
| (4) |
subject to
where C is the cost parameter. The dual problem of (4) is
| (5) |
subject to
where αi, i = 1, …, n, are Lagrange multipliers and C > 0 is the classifier margin. The values of αi, denoted that solve (5), determine the optimal decision function given by, , where β0 is obtained by solving Aisign(Ri) f (Xi) = 1 for any Xi given αi and the estimated optimal rule 𝒟*(X) is sign (f*(X)) (e.g., Hastie et al., 2009, Chapter 12).
2.2. Multiple Kernel Outcome-weighted Learning
The kernel function k (Xi, Xj) provides a measure of similarity between the i-th subject and j-th subject. AOL and OWL both rely on a single pre-determined kernel function to capture this similarity. However, in many modern applications, using a single kernel may not be optimal. Observed data often include measures arising from multiple data domains, and thus a single kernel function may not be sufficient for the purpose of optimizing ITRs. To address this, we propose to apply a multiple kernel approach for two reasons: to allow a different kernel for each data domain; and also to allow for multiple measures of similarity within each domain. Our approach lets the learning process itself select among the multiple candidate kernels:
| (6) |
where kl is a kernel function in a RKHS ℋl, l = 1, …, L, and ηl is the kernel weight of the l-th kernel function. It can be shown that kη is also a RKHS kernel function (Aronszajn, 1950). We require that ηl ≥ 0, l = 1, …, L and also that . In this formulation, ηl represents the relative importance of the l-th kernel.
Suppose that we have M different data domains (or sources or modalities). Let , where denotes the predictors in the m-th data domain.
where is the l-th kernel function used for the m-th data domain, l = 1, …, Lm, and ηm,l are the corresponding kernel weights. For example, in the application to be described in Section 4, the data domains are: demographic characteristics, clinical, behavioral performance, and neuroimaging predictors.
We start with a set of candidate kernel functions km,l. Our aim is to find the optimal treatment rule with respect to kernel weights ηm,l and Lagrange multipliers α.
We solve the optimization problem:
| (7) |
subject to
The estimated decision function is then
where is obtained by solving Aisign (Ri) f (Xi) = 1 for any Xi for . The estimated decision rule is . The constraints on ηm,l (i.e., ηm,l ≥ 0 and ) induces model sparsity and enables us to both identify informative data domains and select appropriate kernels (i.e., those with ) for each data domain. When M = 1, L1 = 1, and , this approach reduces to (5). To solve (7), we use the MKL algorithm in Rakotomamonjy et al. (2008). We call the resulting method Outcome Weighted Multiple Kernel Learning (OWMKL).
3. Simulation Studies
We evaluated our method through several simulation scenarios with sample sizes of n = 150, 200, 400, 800, 1000 for the training data set. For each simulated dataset, we compared the empirical value function on a validation set of size 100,000 with: 1) OWL using the Gaussian kernel; 2) AOL using the Gaussian kernel; 3) OWL using the linear kernel; 4) AOL using the linear kernel; and 5) Q-learning based on regressing the outcome on X, A, and the interaction term between them X × A.
3.1. Simulation Settings
We model the data for our simulation studies on the structure of the depression data to be described in the next section. To do this, we generate a 50-dimensional vector of Xi for each subject with the 50 total predictors derived from seven data domains of continuous predictors generated from a multivariate normal distribution M V N (0, Σ) where the covariance matrix Σ and distribution of predictors amongst data domains is described in Figure 1. In addition, we generate data from two additional data domains each consisting of a single binary predictor generated from Bernoulli(0.5). The treatment Ai ∈ {−1, 1} is generated independently of Xi with P(Ai = 1) = 0.5.
Fig. 1.
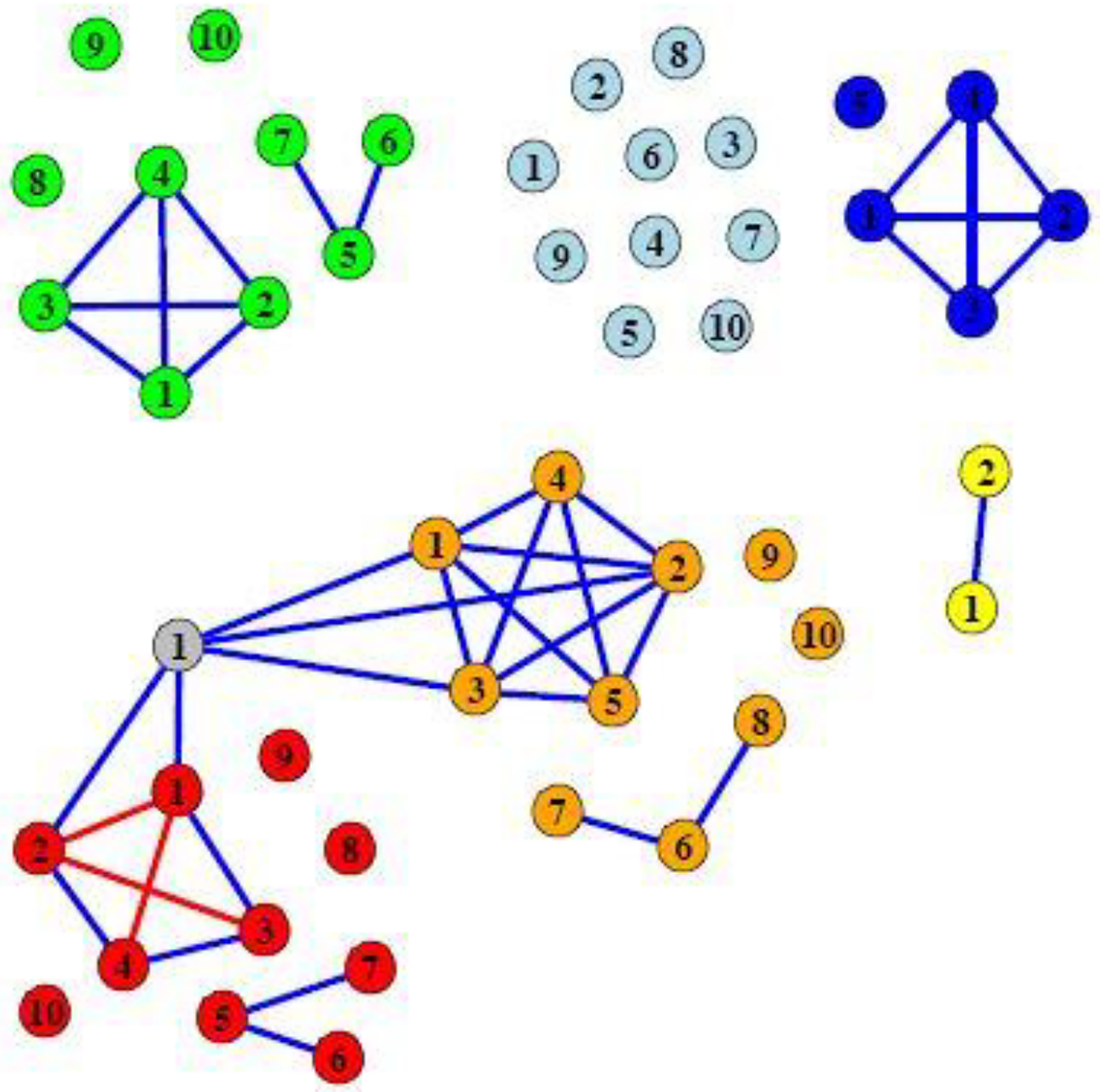
A representation of the covariance matrix Σ of the continuous predictors in the simulations. Each node represents one predictor. An edge between two predictors indicates that the covariance between the two predictors is 0.3. If there is no edge between two predictors, the pair is independent. The diagonal elements of Σ are 1. The node color indicates data domain membership. Orange: Data domain 1; Red: Data domain 2; Light blue: Data domain 3; Green: Data domain 4; Blue: Data domain 5; Yellow: Data domain 6; Grey: Data domain 7.
The outcome was generated from . We generated the Ti terms according to six different scenarios, described in Table 1. Thus Ti × Ai is the interaction term between predictors and treatment. Also, ϵi is the error term generated independently of all other variables from a N(0, 1) distribution. In order to assess how well our approach is able to discriminate between data domains that are useful for treatment determination from those who are not, in all settings, Ti depends only on data domain 1 and data domain 2 .
Table 1.
Simulation Settings. The last column refers to the percentage of the population for whom Treatment 1 would be more beneficial than Treatment −1
| Setting | T i | Treatment 1 benefit |
|---|---|---|
| 1 (linear) | 60% | |
| 2 (quadratic) | 60% | |
| 3 (quadratic, more predictors) | 80% | |
| 4 (quadratic, weak signal) | 60% | |
| 5 (two-way interaction) | 50% | |
| 6 (exponential) | 70% |
For our implementation of OWMKL, we used four kernels for each of the data domains which included multiple continuous predictors. The four kernels are: a linear kernel ; a quadratic kernel, ; a cubic kernel, ; and a Gaussian kernel . A linear kernel and a Gaussian kernel were used for which included a single continuous predictor. Indicator kernels were used for and which included a binary predictor (Daemen and De Moor, 2009). The bandwidth d in Gaussian kernel function in OWMKL, OWL using the Gaussian kernel, and AOL using the Gaussian kernel is predetermined by the median heuristic (the median of ) (Fukumizu et al., 2009; Caputo et al., 2002). The only tuning parameter in the algorithm is C which was chosen by a two-fold cross-validation that maximizes the empirical value function
| (8) |
on the training set in OWMKL, AOL, and OWL. A grid search was used to determine C in OWMKL from the grid (22, 23, …, 210); the grid searches for AOL and OWL were over (2−15, 2−14, …, 215). Simulations were repeated 100 times for each setting. We calculated the empirical value function (8) under the estimated optimal treatment rule for each method on the validation set.
3.2. Simulation Results
Figure 2 shows the results of the simulation experiment. The performance of OWL and AOL using the Gaussian kernel is not better than that of using the linear kernel. Thus, we provide boxplots of the empirical value functions for OWL using the linear kernel, AOL using the linear kernel, Q-learning, and OWMKL. For reference, we also indicate the results of three alternative treatment rules: all subjects are assigned treatment 1; all subjects are assigned treatment −1; and subjects are assigned each treatment on the basis of a fair coin toss. We also indicate the “true” optimal bound that would assign the treatment with larger Ti × Ai to subject i if the true Ti were known.
Fig. 2.
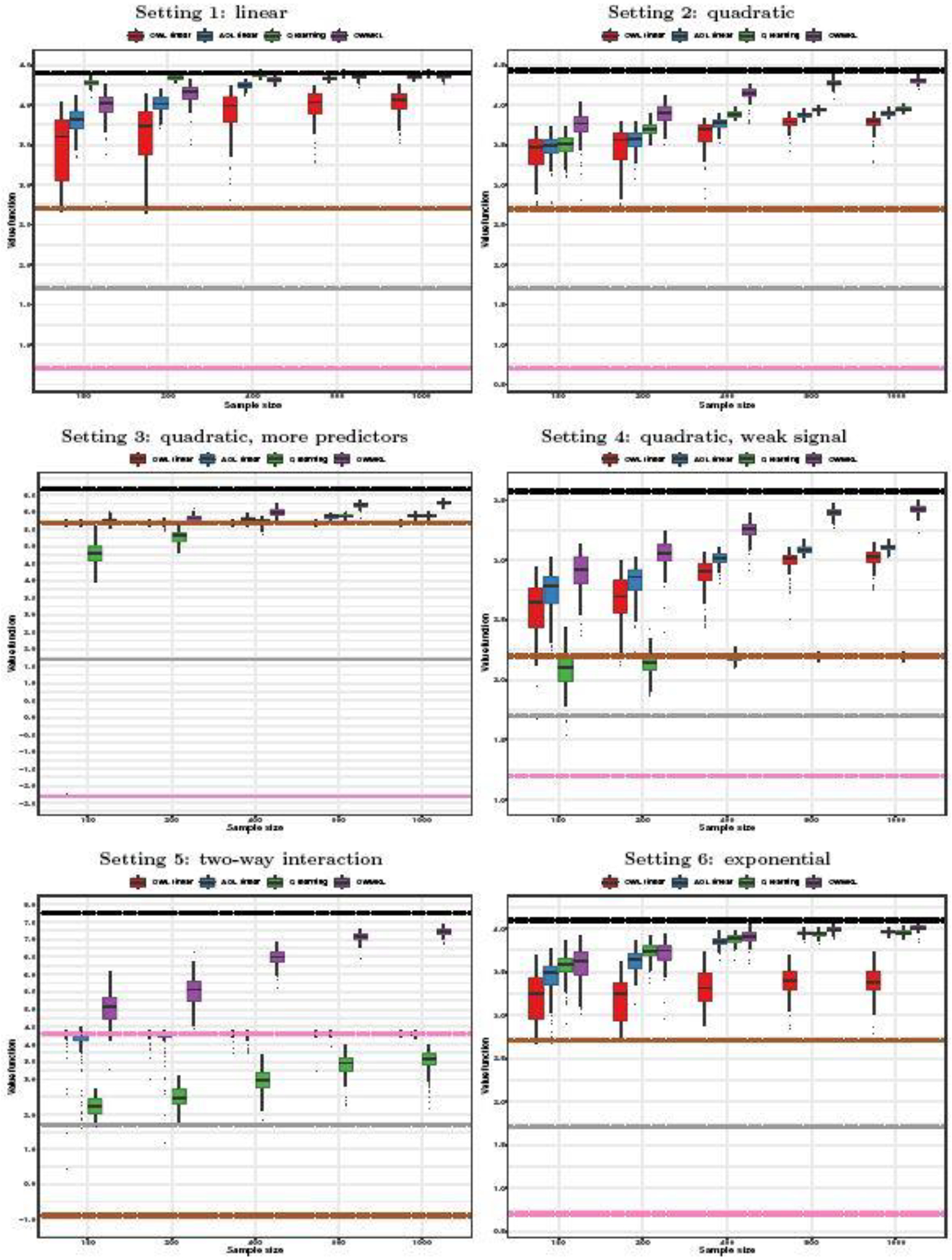
Boxplots of empirical value function in simulations. Black lines: true optimal bound; Grey lines: coin toss; Brown lines: all treatment 1; Pink lines: all treatment −1; Solid line: median of value function across simulations; Upper dash line: 75% quantile of value function across simulations; Lower dash line: 25% quantile of value function across simulations.
For Setting 1 in which Ti is a linear function of Xi, as would be expected, the Q-learning approach performed the best among those considered. Among the rest, OWMKL came out ahead of the others in terms of larger median empirical value function and smaller standard deviation. When the sample size increased to n = 800 and n = 1000, results for OWMKL were nearly as good as those for Q-learning.
For Settings 2–6, OWMKL tended to perform well relative to the other methods. For Settings 2–4 in which Ti included the quadratic terms of Xi, OWMKL resulted in the largest empirical value function, which increased at a faster rate for larger n, and nearly reached the optimal bound for large sample sizes. The empirical value functions of OWL, AOL, and Q-learning tended to increase more slowly for larger n. Q-learning performed the worst when the sample size was small in Setting 3. Its performance was even worse than assigning all subjects to treatment 1 in Setting 4 and was not improved much when the sample size was increased. In Setting 5 when Ti included two-way interaction terms of Xi, OWMKL had much larger empirical value function than the other methods, while the performances of OWL and AOL were almost the same as the policy of assigning all subjects to treatment −1 and did not improve much with increasing sample size.
In addition, OWMKL tended to correctly identify the relevant data domains (i.e., those that contribute to determination of optimal treatment) while the other methods are not intended to be able to do this. To illustrate this point, we calculated the data domain kernel weight for each data domain, m = 1, …, 9 and summarized the average data domain kernel weights across 100 simulations in Table 2. The kernel weights of data domains 1 and 2 were the top two largest and were much larger compared to the kernel weights of other data domains.
Table 2.
Average data domain kernel weights across 100 simulations from OWMKL.
| Data | Data | Data | Data | Data | Data | Data | Data | Data | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Setting | n | domain 1 | domain 2 | domain 3 | domain 4 | domain 5 | domain 6 | domain 7 | domain 8 | domain 9 |
| Setting 1 | 150 | 0.258 | 0.416 | 0.086 | 0.086 | 0.064 | 0.082 | 0.004 | 0.002 | 0.002 |
| 200 | 0.294 | 0.443 | 0.064 | 0.064 | 0.067 | 0.062 | 0.003 | 0.001 | 0.001 | |
| 400 | 0.335 | 0.391 | 0.068 | 0.068 | 0.086 | 0.050 | 0.001 | 0.001 | 0.001 | |
| 800 | 0.372 | 0.442 | 0.048 | 0.047 | 0.053 | 0.036 | 0.000 | 0.000 | 0.000 | |
| 1000 | 0.370 | 0.427 | 0.057 | 0.054 | 0.054 | 0.037 | 0.000 | 0.000 | 0.000 | |
| Setting 2 | 150 | 0.346 | 0.269 | 0.089 | 0.078 | 0.103 | 0.083 | 0.030 | 0.001 | 0.002 |
| 200 | 0.377 | 0.285 | 0.093 | 0.067 | 0.080 | 0.066 | 0.028 | 0.002 | 0.002 | |
| 400 | 0.358 | 0.363 | 0.072 | 0.066 | 0.072 | 0.052 | 0.017 | 0.000 | 0.000 | |
| 800 | 0.332 | 0.452 | 0.056 | 0.055 | 0.054 | 0.037 | 0.013 | 0.000 | 0.000 | |
| 1000 | 0.332 | 0.483 | 0.046 | 0.045 | 0.045 | 0.036 | 0.012 | 0.000 | 0.000 | |
| Setting 3 | 150 | 0.249 | 0.180 | 0.149 | 0.146 | 0.121 | 0.148 | 0.005 | 0.001 | 0.002 |
| 200 | 0.283 | 0.183 | 0.148 | 0.129 | 0.145 | 0.108 | 0.003 | 0.001 | 0.001 | |
| 400 | 0.280 | 0.267 | 0.100 | 0.120 | 0.156 | 0.072 | 0.004 | 0.001 | 0.001 | |
| 800 | 0.284 | 0.275 | 0.106 | 0.113 | 0.159 | 0.062 | 0.001 | 0.000 | 0.000 | |
| 1000 | 0.253 | 0.270 | 0.109 | 0.125 | 0.169 | 0.072 | 0.001 | 0.000 | 0.000 | |
| Setting 4 | 150 | 0.395 | 0.268 | 0.076 | 0.069 | 0.096 | 0.073 | 0.020 | 0.001 | 0.002 |
| 200 | 0.424 | 0.275 | 0.067 | 0.069 | 0.092 | 0.058 | 0.013 | 0.002 | 0.001 | |
| 400 | 0.441 | 0.278 | 0.065 | 0.064 | 0.089 | 0.051 | 0.010 | 0.000 | 0.001 | |
| 800 | 0.513 | 0.291 | 0.051 | 0.049 | 0.051 | 0.036 | 0.007 | 0.000 | 0.001 | |
| 1000 | 0.520 | 0.298 | 0.047 | 0.046 | 0.050 | 0.032 | 0.006 | 0.000 | 0.000 | |
| Setting 5 | 150 | 0.229 | 0.362 | 0.110 | 0.111 | 0.098 | 0.080 | 0.005 | 0.003 | 0.003 |
| 200 | 0.281 | 0.372 | 0.073 | 0.083 | 0.115 | 0.070 | 0.005 | 0.001 | 0.001 | |
| 400 | 0.321 | 0.279 | 0.093 | 0.076 | 0.162 | 0.067 | 0.001 | 0.001 | 0.000 | |
| 800 | 0.401 | 0.282 | 0.084 | 0.081 | 0.098 | 0.053 | 0.001 | 0.000 | 0.000 | |
| 1000 | 0.434 | 0.285 | 0.080 | 0.079 | 0.074 | 0.048 | 0.001 | 0.000 | 0.000 | |
| Setting 6 | 150 | 0.458 | 0.189 | 0.087 | 0.095 | 0.085 | 0.075 | 0.006 | 0.003 | 0.003 |
| 200 | 0.467 | 0.197 | 0.088 | 0.078 | 0.099 | 0.063 | 0.006 | 0.001 | 0.002 | |
| 400 | 0.478 | 0.309 | 0.049 | 0.045 | 0.075 | 0.037 | 0.005 | 0.001 | 0.002 | |
| 800 | 0.458 | 0.341 | 0.044 | 0.048 | 0.073 | 0.032 | 0.004 | 0.001 | 0.000 | |
| 1000 | 0.454 | 0.351 | 0.051 | 0.052 | 0.059 | 0.029 | 0.002 | 0.000 | 0.001 |
The computational time of OWMKL was about twice of that of AOL approach in our simulation studies since we used 28 kernel functions in total. For instance, the average running time of one simulation when sample size was 1000 was 70 seconds on an Intel Core i9 3.6 GHz processor. In practice, the users can specify a fewer number of candidate kernel functions to reduce computational burden.
4. Application
Major Depressive Disorder (MDD) is a common mental disorder and a leading cause of disability as indicated by the Global Burden of Disease. MDD patients display large heterogeneity in their clinical symptoms, course of illness, and response to treatment (Fava and Kendler, 2000; Belmaker and Agam, 2008). Establishing Moderators and Biosignatures of Antidepressant Response in Clinical Care (EMBARC) was a clinical trial that recruited patients who had recurrent and early onset MDD (Trivedi et al., 2016). In this study, patients were randomly assigned to receive either sertraline or placebo for 8 weeks with π(A) = 0.5. Study investigators collected a comprehensive set of clinical, behavioral, and neuroimaging predictors for each patient. We used 43 predictors in this illustration (Appendix Table A1). The clinical outcome is the change score of the Hamilton Depression scale (HAMD17) between baseline visit and at Week 8. (Larger change scores correspond to better outcomes.) Missing predictors were imputed using multivariate imputation by chained equations (MICE) (Petkova et al., 2017; van Buuren and Groothuis-Oudshoorn, 2011) before the analysis. A total of 242 patients were included in the analysis.
An indicator kernel was used for the binary variables gender and hypersomnia. Linear and Gaussian kernels were used for age which was treated as a single continuous variable. We followed the variable category conventions of Petkova et al. (2017) defining the first tier baseline characteristics to group the variables as follows: 16 clinical variables; 8 behavioral performance variables; 2 structural magnetic resonance imaging (sMRI) variables; 10 functional MRI variables including both resting state and task-based predictors; 3 electroencephalography (EEG) variables; and 1 diffusion tensor imaging (DTI) variable. A linear kernel, a quadratic kernel, a cubic kernel, and a Gaussian kernel were used for each data domain.
We randomly selected two thirds of the subjects as our training set (161 subjects) and left the remaining one third as the validation data (81 subjects). The only tuning parameter C was chosen within the training set by 10-fold cross validation with searching grid from 22 to 215. We repeated the analysis 100 times by randomly assigning observations to the training and validation data sets. We compared the OWMKL approach with OWL, AOL, and Q-learning. Also, for reference we considered the policies of assigning all patients to sertraline; assigning all patients to placebo; and random assignment. The bandwidth for the Gaussian kernel in OWMKL, OWL using the Gaussian kernel, and AOL using the Gaussian kernel was calculated before the analysis by the heuristic median (Fukumizu et al., 2009; Caputo et al., 2002) based on the full data; the searching grid for C in OWL and AOL was from 2−15 to 215.
The empirical value functions of each method across the 100 bootstrap samples are shown in Figure 3. In terms of the mean and median value of empirical value functions, OWMKL outperformed all the other methods. Standard deviations of all methods were similar (Table 3). Figure 4 visualizes the proportion subjects assigned to sertraline by each method across 100 bootstrap samples. Both OWL using the Gaussian kernel and AOL using the Gaussian kernel assigned all subjects to the same treatment group in each bootstrap and more frequently assigned subjects to sertraline, matching the ‘one-size-fits-all’ policy. The Q-learning policy was more similar to the coin toss policy, with the proportion of subjects assigned to sertraline ranging from 0.42 to 0.74 with a median 0.58. In contrast, the OWMKL policy varied across 100 bootstrap samples which, suggesting that the OWMKL treatment rules are more reflective of each subject’s characteristics.
Fig. 3.
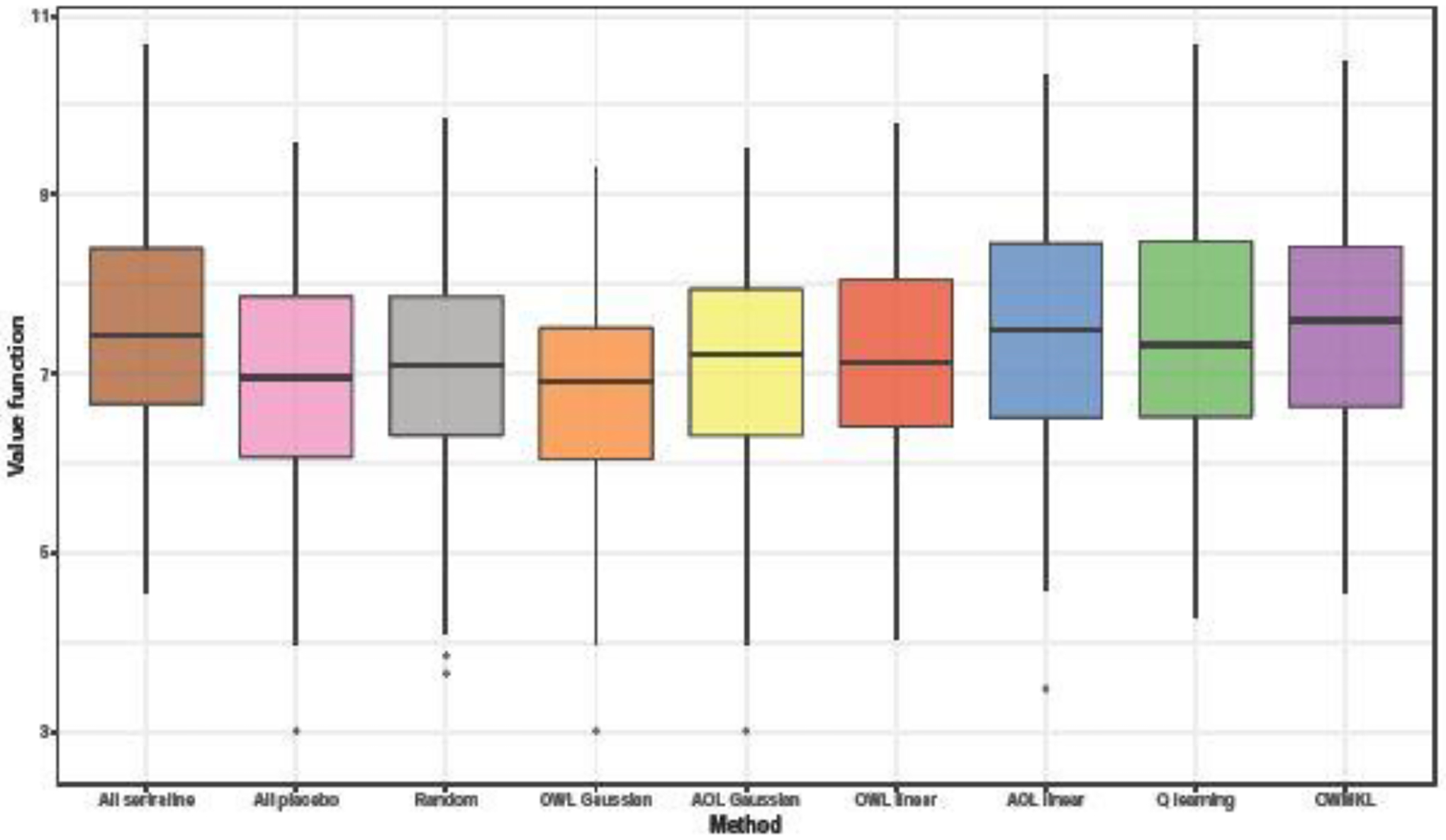
Boxplots of empirical value function across 100 bootstrap samples in EMBARC study.
Table 3.
Summary of empirical value functions over 100 bootstrap samples.
| All | All | OWL | AOL | OWL | AOL | Q | |||
|---|---|---|---|---|---|---|---|---|---|
| sertraline | placebo | Random | Gaussian | Gaussian | linear | linear | learning | OWMKL | |
| Mean | 7.437 | 6.912 | 7.020 | 6.787 | 7.083 | 7.186 | 7.451 | 7.486 | 7.535 |
| Median | 7.420 | 6.963 | 7.086 | 6.914 | 7.210 | 7.136 | 7.494 | 7.321 | 7.593 |
| Standard deviation | 1.202 | 1.269 | 1.314 | 1.204 | 1.256 | 1.152 | 1.244 | 1.324 | 1.295 |
Fig. 4.
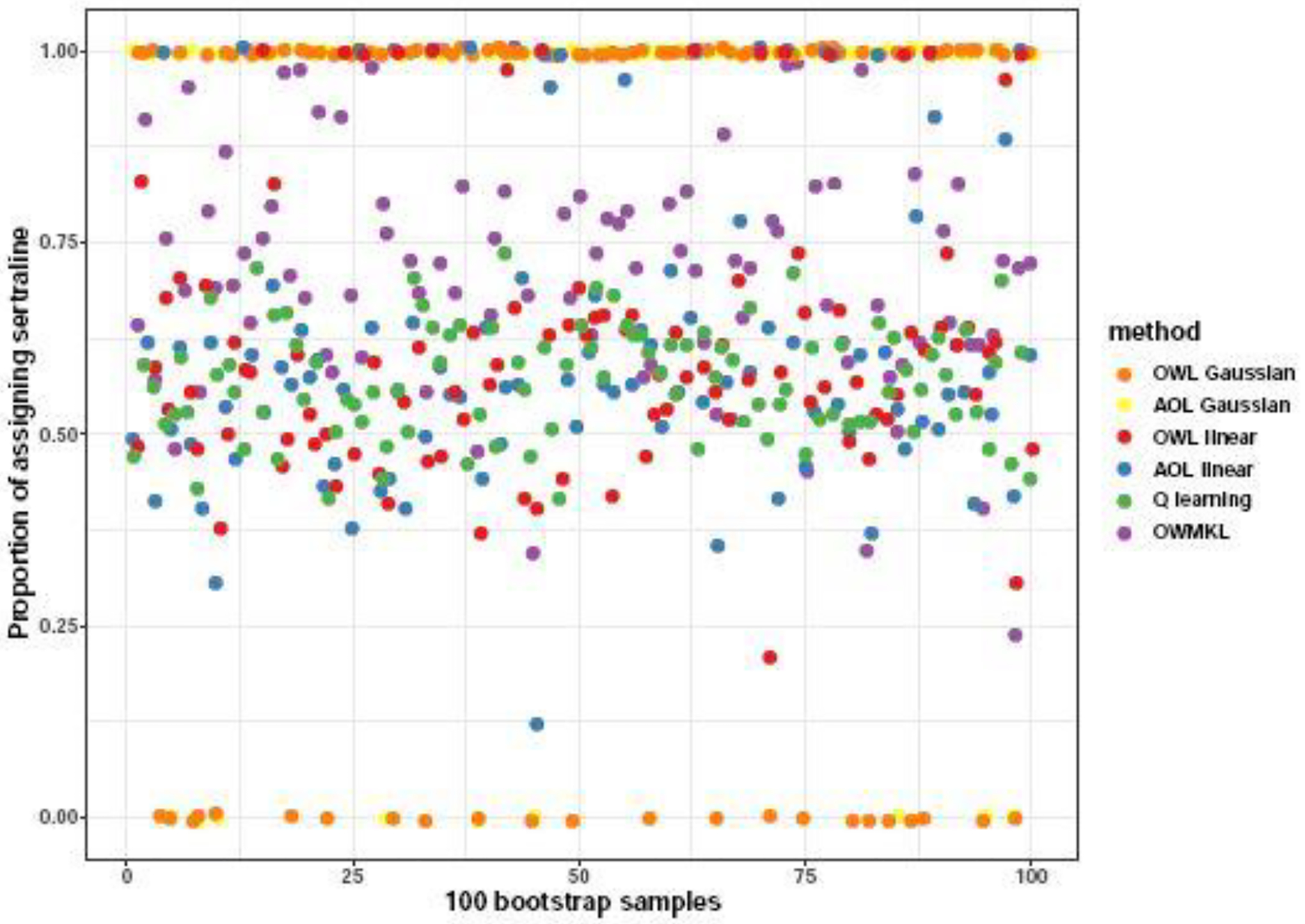
The proportion of subjects assigned to sertraline by each method across 100 bootstrap samples in the EMBARC study.
In order to assess the relative importance of the different data domains, we calculated the data domain kernel weights (Table 4). In this table, we report, for each data domain, the average weights across the 100 bootstrap samples and the weights obtained from applying the procedure once to the entire dataset, where tuning parameter was chosen based on the average 10-fold cross validation value function across 100 bootstrap samples of the entire dataset. The clinical data domain had the largest average kernel weight over 100 bootstrap samples followed by the behavioral performance data domain. Thus, the clinical and behavior data domains contributed the most to determining the optimal treatment for patients. The kernel weights of neuroimaging data domains were relatively small, especially DTI. Since it is somewhat expensive to collect neuroimaging predictors, these results suggest that we may not need to measure DTI in order to make treatment decisions. If a data domain kernel weight threshold is set at 0.1, sMRI, EEG, and fMRI predictors will be additionally utilized in the ITR. In terms of time and resource utilization, it is not much more difficult to measure all 10 fMRI measures than just to measure one or two of them. Thus, we emphasize that for clinical applications, it is sometimes more important to identify data domains instead of individual variables.
Table 4.
Estimated data domain kernel weights from OWMKL.
| Data | Number | Average kernel weights | Kernel weights |
|---|---|---|---|
| domain | of variables | over 100 bootstrap samples | on entire data |
| Gender | 1 | 0.001 | 0 |
| Hypersomnia | 1 | 0 | 0 |
| Age | 1 | 0.005 | 0.006 |
| Clinical | 16 | 0.368 | 0.827 |
| Behavioral Performance | 8 | 0.244 | 0.043 |
| sMRI | 2 | 0.123 | 0.039 |
| fMRI | 10 | 0.122 | 0.042 |
| EEG | 3 | 0.120 | 0.036 |
| DTI | 1 | 0.016 | 0.007 |
When applying the procedure once to the entire dataset, the clinical data domain still had the largest kernel weight 0.827 while behavioral performance, sMRI, fMRI, and EEG had similar kernel weight around 0.04. We further investigated the data domain importance by only using clinical data and one of behavioral performance, sMRI, fMRI, and EEG data. The kernel weight of clinical data domain was 1 when using it with behavioral performance, or sMRI, or EEG. When using clinical data with fMRI, the kernel weight of clinical data domain was 0.16 and that of fMRI was 0.84. In clinical practice, we recommend only collecting clinical data considering the fMRI brain scan cost.
5. Discussion
In this work, we proposed OWMKL to estimate ITRs by using multiple kernels to model the relationships between baseline data domains and an outcome variable. The multiple kernel functions can be regarded as a set of basis kernel functions that represent different notions of similarity measures across multiple data domains. Our method finds a composite kernel function in an optimal fashion that can better accommodate the similarity of predictors within data domains rather than choosing any single specific kernel function (a single similarity representation). When multiple data domains are available, our method integrates prior data domain knowledge to group predictors that are within the same data domain and takes into account the heterogeneity across different data domains. The choice of kernels is flexible and can be determined based on the types of data domains. In addition, some predictors may not be useful for choosing an optimal treatment rule. Our approach introduces sparsity to handle high-dimensional variables that can distinguish informative data domains from non-informative data domains. This can result in a significant savings in terms of time and expense for patients by eliminating the collection of non-informative data domains. In addition, since the cost and time of measuring several neuroimaging measures from the same data domain is about the same as that of extracting a single measure from the domain, it is most important to identify useful data domains as opposed to single measures from the domains. If one is interested in selecting specific predictors that may be important rather than identifying entire data domains, our approach can be adapted to use separate kernel functions for the specific predictors.
The application of OWMKL to the EMBARC depression study illustrated that the clinical data domain is most informative for choosing an optimal treatment rule. These OWMKL results suggest that it may be sufficient for clinicians to collect data only from the one easily obtained and inexpensive data domain and avoid the collection from the more expensive neuroimaging data domains.
Several extensions can be considered. For instance, it would be interesting to explore which type of kernels are optimal for various data domains (e.g., scalar, matrix-valued, functional data). In our simulation experiment and in our depression example, only scalar data domains were used. Also, we only considered a two-arm clinical trial in this work. In trials with more treatment arms, our method can be easily generalized to a weighted multi-group classification problem under the MKL framework (Rakotomamonjy et al., 2008). We could also extend our method for a continuous treatment variable, such as dose level, by solving a weighted regression problem with multiple kernels (Rakotomamonjy et al., 2008). Furthermore, we can consider extending our method from the single-stage decision making setting to estimate dynamic treatment regimes.
Supplementary Material
Acknowledgments
This work was partially supported by National Institute of Mental Health Grant 5 R01 MH099003. Xie was also supported by the Center of Statistical Research and the Joint Lab of Data Science and Business Intelligence at the Southwestern University of Finance and Economics, and the Guanghua talent project of Southwestern University of Finance and Economics.
Footnotes
SUPPLEMENTARY MATERIAL
Matlab toolbox for OWMKL: Matlab toolbox OWMKL containing code to perform OWMKL, AOL, and OWL described in the article. The toolbox also contains the simulation examples in the article. A ‘readme’ file describes the instructions. (Matlab-OWMKL.zip)
Appendix Table A1: Predictors used in EMBARC analysis as mentioned in Section 4. (OWMKL-Appendix.pdf)
Contributor Information
Shanghong Xie, School of Statistics, Southwestern University of Finance and Economics; Department of Biostatistics, Mailman School of Public Health, Columbia University.
Thaddeus Tarpey, Division of Biostatistics, Department of Population Health, New York University.
Eva Petkova, Division of Biostatistics, Department of Population Health, New York University.
R. Todd Ogden, Department of Biostatistics, Mailman School of Public Health, Columbia University.
References
- Aronszajn N (1950). Theory of reproducing kernels. Transactions of the American Mathematical Society, 68(3):337–404. [Google Scholar]
- Bach FR (2008). Consistency of the group lasso and multiple kernel learning. Journal of Machine Learning Research, 9:1179–1225. [Google Scholar]
- Bach FR, Lanckriet GR, and Jordan MI (2004). Multiple kernel learning, conic duality, and the SMO algorithm. In Proceedings of the Twenty-first International Conference on Machine Learning, page 6. ACM. [Google Scholar]
- Belmaker R and Agam G (2008). Major depressive disorder. New England Journal of Medicine, 358(1):55–68. [DOI] [PubMed] [Google Scholar]
- Berlinet A and Thomas-Agnan C (2011). Reproducing kernel Hilbert spaces in probability and statistics. Springer Science & Business Media. [Google Scholar]
- Caputo B, Sim K, Furesjo F, and Smola A (2002). Appearance-based object recognition using SVMs: which kernel should I use? Procedings of NIPS Workshop on Statistical Methods for Computational Experiments in Visual Processing and Computer Vision, 2002. [Google Scholar]
- Daemen A and De Moor B (2009). Development of a kernel function for clinical data. In Annual International Conference of the IEEE Engineering in Medicine and Biology Society, pages 5913–5917. [DOI] [PubMed] [Google Scholar]
- Fava M and Kendler KS (2000). Major depressive disorder. Neuron, 28(2):335–341. [DOI] [PubMed] [Google Scholar]
- Fukumizu K, Gretton A, Lanckriet GR, Schölkopf B, and Sriperumbudur BK (2009). Kernel choice and classifiability for RKHS embeddings of probability distributions. In Advances in Neural Information Processing Systems, pages 1750–1758. [Google Scholar]
- Gönen M and Alpayd in E (2011). Multiple kernel learning algorithms. Journal of Machine Learning Research, 12:2211–2268. [Google Scholar]
- Hastie T, Tibshirani R, and Friedman J (2009). The elements of statistical learning: data mining, inference, and prediction. Springer Science & Business Media. [Google Scholar]
- Kang C, Janes H, and Huang Y (2014). Combining biomarkers to optimize patient treatment recommendations. Biometrics, 70(3):695–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanckriet GR, Cristianini N, Bartlett P, Ghaoui LE, and Jordan MI (2004a). Learning the kernel matrix with semidefinite programming. Journal of Machine Learning Research, 5:27–72. [Google Scholar]
- Lanckriet GR, De Bie T, Cristianini N, Jordan MI, and Noble WS (2004b). A statistical framework for genomic data fusion. Bioinformatics, 20(16):2626–2635. [DOI] [PubMed] [Google Scholar]
- Lanckriet GR, Deng M, Cristianini N, Jordan MI, and Noble WS (2004c). Kernel-based data fusion and its application to protein function prediction in yeast. Pacific Symposium on Biocomputing, 9:300–311. [DOI] [PubMed] [Google Scholar]
- Liu Y, Wang Y, Kosorok MR, Zhao Y, and Zeng D (2018). Augmented outcome-weighted learning for estimating optimal dynamic treatment regimens. Statistics in Medicine, 37(26):3776–3788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkova E, Ogden RT, Tarpey T, Ciarleglio A, Jiang B, Su Z, Carmody T, Adams P, Kraemer HC, Grannemann BD, et al. (2017). Statistical analysis plan for stage 1 EMBARC (establishing moderators and biosignatures of antidepressant response for clinical care) study. Contemporary Clinical Trials Communications, 6:22–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian M and Murphy SA (2011). Performance guarantees for individualized treatment rules. Annals of Statistics, 39(2):1180–1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakotomamonjy A, Bach FR, Canu S, and Grandvalet Y (2008). SimpleMKL. Journal of Machine Learning Research, 9:2491–2521. [Google Scholar]
- Shi C, Song R, Lu W, and Fu B (2018). Maximin projection learning for optimal treatment decision with heterogeneous individualized treatment effects. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 80(4):681–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trivedi MH, McGrath PJ, Fava M, Parsey RV, Kurian BT, Phillips ML, Oquendo MA, Bruder G, Pizzagalli D, Toups M, Cooper C, Adams P, Weyandt S, Morris DW, Grannermann BD, Ogden RT, Buckner R, Mclnnis M, Kraemer HC, Petkova E, Carmody TJ, and Weissman MM (2016). Establishing moderators and biosignatures of antidepressant response in clinical care (EMBARC): rationale and design. Journal of Psychiatric Research, 78:11–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Buuren S and Groothuis-Oudshoorn K (2011). mice: Multivariate imputation by chained equations in R. Journal of Statistical Software, 45(3):1–67. [Google Scholar]
- Wu P, Zeng D, Fu H, and Wang Y (2020). On using electronic health records to improve optimal treatment rules in randomized trials. Biometrics, 76(4):1075–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B, Tsiatis AA, Davidian M, Zhang M, and Laber E (2012a). Estimating optimal treatment regimes from a classification perspective. Stat, 1(1):103–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B, Tsiatis AA, Laber EB, and Davidian M (2012b). A robust method for estimating optimal treatment regimes. Biometrics, 68(4):1010–1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Zeng D, Rush AJ, and Kosorok MR (2012). Estimating individualized treatment rules using outcome weighted learning. Journal of the American Statistical Association, 107(499):1106–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


