Abstract
Motivation
Over the last decade, more diverse populations have been included in genome-wide association studies. If a genetic variant has a varying effect on a phenotype in different populations, genome-wide association studies applied to a dataset as a whole may not pinpoint such differences. It is especially important to be able to identify population-specific effects of genetic variants in studies that would eventually lead to development of diagnostic tests or drug discovery.
Results
In this paper, we propose PopCluster: an algorithm to automatically discover subsets of individuals in which the genetic effects of a variant are statistically different. PopCluster provides a simple framework to directly analyze genotype data without prior knowledge of subjects’ ethnicities. PopCluster combines logistic regression modeling, principal component analysis, hierarchical clustering and a recursive bottom-up tree parsing procedure. The evaluation of PopCluster suggests that the algorithm has a stable low false positive rate (∼4%) and high true positive rate (>80%) in simulations with large differences in allele frequencies between cases and controls. Application of PopCluster to data from genetic studies of longevity discovers ethnicity-dependent heterogeneity in the association of rs3764814 (USP42) with the phenotype.
Availability and implementation
PopCluster was implemented using the R programming language, PLINK and Eigensoft software, and can be found at the following GitHub repository: https://github.com/gurinovich/PopCluster with instructions on its installation and usage.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
In many genetic association studies, the phenotype is a binary variable indicating the presence or absence of a trait, and logistic regression is a popular model used to test the associations between single nucleotide polymorphisms (SNPs) and the phenotype. The model can be used to adjust the association between each SNP and the phenotype by various covariates, including genome-wide principal components that describe the genetic architecture of different ethnic groups (Solovieff et al., 2010).
While non-European ethnicities have been under-represented in genome-wide association studies (GWAS), the number of diverse ethnicities is increasing (Petrovski and Goldstein, 2016; Popejoy and Fullerton, 2016). Comparison of the ancestry distribution of the GWAS catalog from 2009 to 2016 shows, e.g. that the percentage of subjects of European and Jewish ancestry has decreased from 96 to 81%, and the number of subjects of Asian descent has increased from 3 to 14% (Need and Goldstein, 2009; Popejoy and Fullerton, 2016). Although some other ethnic groups are still highly under-represented, their inclusion continues to increase (Mathew et al., 2017).
Population stratification can challenge genetic association studies when the magnitude and/or direction of the effects of the allele as well as the allele frequency vary according to ethnicity (Popejoy and Fullerton, 2016; The PLOS Medicine Editors et al., 2016; Torkamani et al., 2012). For example, the apolipoprotein E (APOE) e4 allele, which is a known risk factor of Alzheimer’s disease, has different allele frequencies and effects in Europeans, Africans and Hispanics (Campos et al., 2013; Corbo and Scacchi, 1999; Hendrie et al., 2014; Liu et al., 2013). Similarly, it has been shown that for 25% of the SNPs associated with BMI, type 2 diabetes and lipid levels in Europeans, the strength of association varies substantially in at least one non-European population (Carlson et al., 2013). Even though a large number of these SNPs may be in linkage disequilibrium (LD) with causal SNPs, it is important to investigate whether any of the associations are due to true population differences rather than differences in LD between populations.
If the association between a SNP and a trait is tested in a group of subjects in which the genetic effect of the SNP varies with ethnicity, ignoring the interaction between the genetic effect and the ethnicity may produce either a false positive (FP) or a false negative (FN) result. For example, if the effects of the SNP are in opposite directions in some ethnic groups, ignoring these antagonistic effects may result in a FN result. An alternative and common situation is when the genetic effect is significant only in a particular genetic background that is over-represented in the analysis. Ignoring the ethnicity effect may produce a FP association in ethnicities in which there is no association between the SNP and phenotype.
In this paper, we introduce PopCluster—an algorithm that finds sub-populations of study subjects in which the genetic effects of a SNP are different. We thoroughly evaluated the false and true positive rates (TPRs) of PopCluster using real and simulated genetic data. We also applied the algorithm to real data from four studies of extreme longevity (EL) and the Health and Retirement Study (HRS). We conclude by reviewing usefulness and limitations of PopCluster, and suggest potential applications.
2 Materials and methods
2.1 Methodology
The algorithm takes the following variables as its input: genome-wide genotype data for each subject, a list of SNPs of interest to test, phenotype information for each subject and a list of covariates to be included in the model, e.g. sex and age. PopCluster takes this information to discover ethnic-specific effects of the list of SNPs of interest by performing the following analyses, which are described in detail in the next sub-sections. First, PopCluster performs principal component analysis (PCA) of the genome-wide genotype data and hierarchical clustering of the most informative principal components to discover a set of nested clusters of genetic ethnicity. Next, genome-wide principal components are recalculated in each cluster of subjects, followed by test of the associations between the phenotype and SNPs in each cluster. The final step of PopCluster is pruning of redundant clusters to generate the final list of SNPs and clusters with varying genetic effects on the phenotype.
2.1.1 Cluster generation
The cluster generation step is depicted in Figure 1. First, PopCluster computes genome-wide principal components using the EIGENSOFT package on the genome-wide genotype data (Price et al., 2006). Next, hierarchical clustering is performed on subjects using the most informative number of principal components. Scree plot is a good way to decide on how many principal components to use (Solovieff et al., 2010). Typically, six principal components are sufficient to characterize the major European ethnic groups, while up to 20 principal components may be needed to characterize more heterogeneous ethnic groups. Since the dendrogram associated with hierarchical clustering is a binary tree, each node (cluster) has at most two children nodes, one parent node and one sibling node, while the ancestors of a node are the parent node and the recursive set of parent nodes. Therefore, a set of nested clusters is generated by sequentially cutting all edges of the dendrogram that describe the agglomerative clustering procedure. Only the clusters with more than 100 subjects, and with a sibling node cluster with more than 100 subjects are included in the subsequent analyses. Figure 1 contains an example of a dendrogram showing hierarchical clusters of 500 subjects. Each node in the dendrogram represents a cluster and the number at each node is the size of the cluster. Clusters 110, 240, 350, 150, 500 above the red, dashed line have over 100 subjects and have a sibling node with over 100 subjects and are used in the next step of the algorithm. We chose 100 as the default minimum number of subjects in a cluster to be taken in the next step of the analysis in order to have an average of 25 observations in a 2 × 2 table for allelic association. This threshold can be easily set to a different value if needed in the input argument list to PopCluster.
Fig. 1.
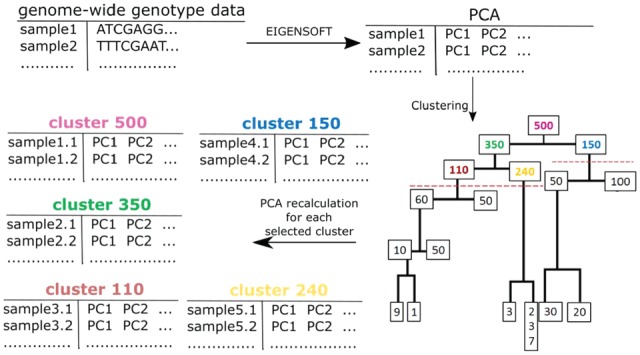
Generation of clusters using genome-wide principal components. (top left-to-right arrow): PopCluster calculates principal components from the genome-wide genotype data using the EIGENSOFT software. (middle top-to-down arrow): subjects are clustered based on a set of principal components using the hierarchical clustering. (bottom left-to-right arrow): PopCluster recalculates principal components for each selected cluster
In each selected cluster, PopCluster recalculates new principal components using the EIGENSOFT package (Price et al., 2006) in order to more specifically describe the genetic structure of the individuals in every new sub-cluster. In our example in Figure 1, PopCluster recalculates the new principal components for clusters: 500, 150, 350, 110 and 240.
2.1.2 Test of the associations between the phenotype and SNPs
Next, PopCluster fits logistic regression models to test the associations between the phenotype and each SNP in every cluster:
| (1) |
where P is the probability of a subject having the phenotype usually expressed as 0 for its absence and 1 for presence; are model parameters; and the variable SNP is typically coded by the number of coded alleles in the genotypes, i.e. additive genetic model. The model is adjusted by PC1,…, PCn and additional covariates x1,…, xm. The statistics from the logistic regression models, such as parameter estimates, standard errors and P-values, are saved by PopCluster for further analysis. The summary of this step is shown in Figure 2.
Fig. 2.
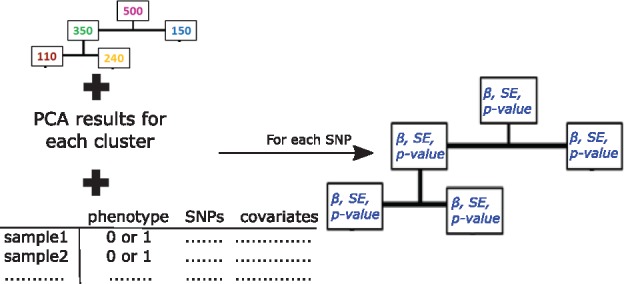
Test of the associations between the phenotype and SNPs in each cluster. Logistic regression models are fit for each SNP-cluster combinations, and the respective statistics from the models are saved for the next step of PopCluster
2.1.3 Pruning of redundant clusters
PopCluster was developed to identify SNPs that have varying effects in different ethnic groups, or sub-populations. Therefore, the core of PopCluster is a recursive algorithm to discover such clusters by comparing the genetic effect of each SNP in the sub-populations represented by two sibling clusters. PopCluster recursively parses the dendrogram bottom-up for every SNP under investigation by comparing the genetic effects of each pair of sibling clusters that have no children (Fig. 3).
Fig. 3.
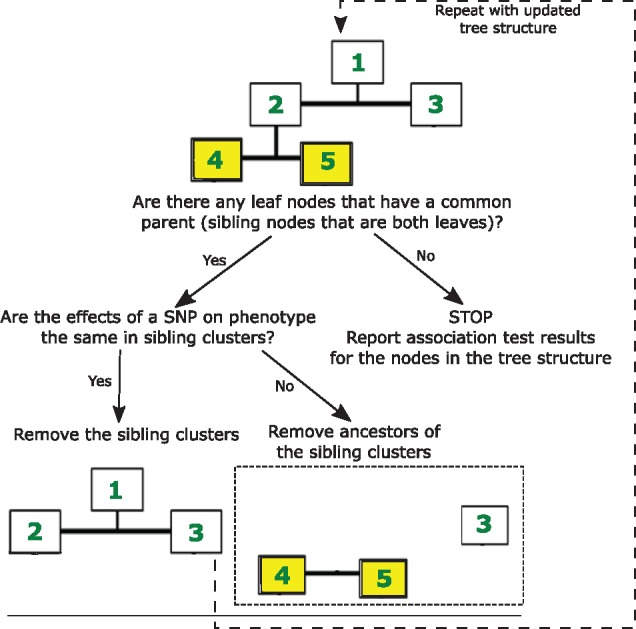
A schematic of the recursive pruning of redundant clusters. The dendrogram describing the final cluster in Figure 2 is recursively parsed bottom-up to identify clusters in which the genetic effects are not statistically different. Here, numbers in the dendrogram (1, 2, 3, 4 and 5) are simply labels to distinguish between different clusters
The algorithm first checks the following conditions for each pair of sibling clusters that have no children: (i) each cluster has at least five cases and five controls; (ii) the minor allele frequency (MAF) of a SNP in each cluster is >0.05; (iii) one or both of the phenotype-SNP associations are statistically significant (P-value <0.05). All of these conditions are user defined input parameters. If at least one of these conditions does not hold, PopCluster removes these sibling nodes from the list of clusters. Otherwise, PopCluster compares the SNPs’ effects in the two sub-populations by calculating the statistic:
| (2) |
where and are SNP effect estimates for two sibling clusters using the logistic regression model in Equation (1), and and are their standard errors. Under the assumption of at least 100 observations per cluster, the estimates and are approximately normally distributed and independent and therefore under the null hypothesis of no difference of the genetic effects.
Therefore, if , where is the percentile of the standard normal distribution, then we fail to reject the null hypothesis. In this case, β1.1 is statistically equivalent to β1.2, thus implying that the effects of the tested SNP in the two sibling clusters are equivalent, and PopCluster merges these nodes into their parent cluster, and removes them from the dendrogram. If then β1.1 ≠ β1.2, and the results from the sibling nodes are included in the list of final results, and all the ancestors of these nodes are removed from the dendrogram.
The procedure parses the dendrogram until there are no sibling nodes that are both leaf nodes. The procedure is repeated separately for each SNP, and the output of PopCluster is a list of clusters for each SNP with all the relevant statistics. These clusters are non-overlapping, meaning no cluster has subjects that are in another cluster and each of the subjects of the initial dataset is included in one of the clusters. If no population-specific effects are identified, the algorithm returns the original top cluster.
Reported SNP–phenotype associations are considered significant if the association between a SNP and the phenotype [β1 in the Equation (1)] in a cluster has a P-value less than a threshold α:
| (3) |
where M is the total number of clusters that was reported by PopCluster for the SNP and N is the number of SNPs tested. By dividing 0.05 by M and N, we adjust the result for multiple comparisons.
2.2 Genotype and phenotype data
We used two different phenotypes and two distinct genome-wide genotype datasets to evaluate our algorithm. The first dataset is compiled from four case-control studies of EL: the New England Centenarian Study (Sebastiani and Perls, 2012), the Southern Italian Centenarian Study (Malovini et al., 2011), the Longevity Gene Project (LGP) (Atzmon et al., 2004) and the Long Life Family Study (LLFS) (Newman et al., 2011) (Table 1). LLFS data are available via dbGaP (dbGaP Study Accession: phs000397.v1.p1). The genotype data for all studies were generated using Illumina SNP arrays (Sebastiani et al., 2012) and imputed to the 1000 Genomes haplotypes phase I using IMPUTE2 following the standard protocol and quality control (Howie et al., 2012). All subjects provided informed consent approved by the study institutional review boards. The combined datasets contain several European ethnicities that have been well characterized. See Supplementary Figure S1 in Sebastiani et al. (2017b) for a characterization of European ethnicities in this dataset using PCA. Cases are defined as individuals who lived past the one percentile survival age from the 1900 birth year cohort based on US Social Security Administration cohort life tables (Bell and Miller, 2005), i.e. age 96 and greater for males, and 100 years and greater for females. The details of the genotype data and the phenotype of EL are presented in Sebastiani et al. (2017b), Andersen et al. (2012) and Sebastiani et al. (2016a,b, 2017c).
Table 1.
Summary of studies of EL included in the analysis
| Study | Cases (median age, range) | Controls |
|---|---|---|
| SICS | 174 (100, 96–109) | 540 |
| LGP | 308 (102, 96–113) | 621 |
| LLFS | 572 (100, 96–111) | 2560 |
| NECS | 1084 (103, 96–119) | 3102 |
| Total | 2138 | 6823 |
In this dataset we used PopCluster to analyze a list of 371 SNPs that were previously found to be associated with EL with P-value ¡ 5E-05 (Sebastiani et al., 2017b). To limit the problem of multiple comparisons, we also used PopCluster to re-analyze the association between the 11 SNPs in Table 2 that have been associated with EL with genome-wide significance (P-value ¡ 5E-07) in Sebastiani et al. (2017b).
Table 2.
Subset of SNPs associated with EL
| SNP | Chr | Pos (hg38) | Ref/Alt | Genes |
|---|---|---|---|---|
| rs2008465 | 2 | 10 014 127 | A/G | GRHL1, KLF11 |
| rs28391193 | 4 | 110 236 842 | G/A | ELOVL6, HSBP1P2 |
| rs72834698 | 6 | 26 176 289 | G/A | HIST1H2BD, HIST1H2BE |
| rs3764814 | 7 | 6 150 149 | T/C | USP42 |
| rs7976168 | 12 | 83 044 780 | A/G | TMTC2 |
| rs7185374 | 16 | 48 416 457 | A/C | SIAH1 |
| rs5882 | 16 | 44 888 997 | A/G | CETP |
| rs6857 | 19 | 44 888 997 | C/T | APOE |
| rs59007384 | 19 | 44 893 408 | G/T | TOMM40 |
| rs405509 | 19 | 44 905 579 | T/G | TOMM40, APOE |
| rs769449 | 19 | 44 906 745 | G/A | APOE |
Note: Chr: chromosome; Pos (hg38): position of a SNP in the Genome Reference Consortium Human Reference 38; Ref/Alt: reference and alternative alleles; Genes: closest gene/genes [annotation was done using SnpEff (Cingolani et al., 2012)].
In addition, we applied PopCluster to the multi-ethnic HRS (Sonnega et al., 2014) on the SNPs from Table 2 to search for ethnic-specific genetic effects on surviving past age 90. The HRS includes self-identified ‘White/Caucasian’, ‘Black or African-American’ and a few different groups of ‘Hispanic’ subjects. Controls were subjects with age at last contact ¡ 81. With this definition of cases and controls, the HRS dataset included 866 cases and 8469 controls. The HRS dataset is available through the HRS website (http://hrsonline.isr.umich.edu/) and dbGaP (dbGaP Study Accession: phs000428.v1.p1).
2.3 Evaluation
We evaluated PopCluster using a combination of real and simulated datasets. Here we outline the datasets and metrics used for the evaluation.
2.3.1 FP rate
We used genotype data of SNPs in Table 2 from EL studies (Table 1) as one of the input parameters to PopCluster to evaluate its FP rate (FPR). This list is a subset of the 371 SNPs described in Section 2.2.
In each simulation, we reshuffled the original labels of cases and controls or randomly generated the case/control labels before applying PopCluster. Therefore, by design, all significant associations detected are FPs. Specifically, we used four versions of the original dataset: the original dataset (8961 subjects) with (i) either the same number of cases and controls as in the original data (2138 cases and 6823 controls), and the case/control labels randomly reshuffled in each run, or (ii) a randomly assigned even number of case and control labels: 4480 cases and 4481 controls. In addition, from the original dataset of 8961 subjects, related subjects from the same families were removed by selecting only one case and one control for each family resulting in 7689 subjects. This reduced dataset was used with (iii) either the same number of cases and controls as in the original data (1961 cases and 5728 controls), and the case/control labels randomly reshuffled in each run, or (iv) a randomly assigned even number of case and control labels: 3844/3845 cases and controls. In addition to permuting case/control status in the overall datasets, we also performed two additional simulations in which the permutation of phenotype labels was done within each cluster in (i) the original dataset (8961 subjects), and (ii) the reduced dataset without related individuals (7689 subjects).
We calculated the FPR for a simulation run as
| (4) |
where FP is the number of FPs, TN is the number of true negatives, N is the number of SNPs provided to the algorithm (11 in the case of our particular evaluation), si is the number of clusters (sub-populations) that were detected by PopCluster to have significant associations between a phenotype and an i-th SNP (FP), ki is the total number of clusters detected by PopCluster for an i-th SNP (FP + TN). Correction for multiple comparisons was incorporated in the FPR evaluation by dividing the nominal significance level α by the total number of clusters detected by PopCluster for each SNP [ki in Equation (4)].
2.3.2 TPR
To estimate the TPR of PopCluster, we simulated two scenarios with (i) a true association only in a selected subpopulation of subjects, and (ii) a true association in the whole dataset. We compared the performances of PopCluster and traditional analysis without clustering in both simulated datasets.
In the first scenario, we simulated an allele A to be associated with EL in the selected group of 1905 subjects with 503 cases and 1402 controls characterized by two first genome-wide principal components calculated with the data of the studies in Table 1: and . For the rest of the subjects, the allele was simulated not to be associated with the phenotype (Supplementary Fig. S1). Specifically, for the subjects with and different allele probabilities were assigned to cases and controls as
| (5) |
where P1 is the probability of allele A in cases; P2 is the probability of allele A in controls. The probabilities of allele dosages were generated assuming Hardy–Weinberg equilibrium. Various combinations of probabilities P1 and P2 [Equation (5)] were tested to evaluate sensitivity and specificity of the algorithm to different risk differences. We chose to cover various scenarios with sufficient power with our sample size. For each P1 value, we set the probability of allele A in controls to be , where g is the difference in the allele frequency between cases and controls and . Varying P1 and g resulted in 20 different combinations of probabilities P1 and P2. For the rest of the subjects [ or ( and )], the allele A was simulated to be associated with PC1 and PC2, but not with the phenotype by setting
| (6) |
with , and such that probabilities P3 are not too extreme. The probabilities of allele dosages were again calculated assuming Hardy–Weinberg equilibrium.
Using the simulated allele data, we estimated the rate of PopCluster to discover the true clusters using the proportion of times the algorithm returned at least one cluster with more than 80% subjects from the region of association. In these cases, we evaluated the TPR of PopCluster for each of the simulation sets as
| (7) |
where TP is the number of true associations that PopCluster predicted to be significant (positive). FN is the number of true associations that PopCluster found to be insignificant (negative). We define an association in a cluster to be true if more than 80% of subjects in the cluster are from the region of association. An association was significant if the P-value was less than a threshold α [Equation (3)]. We also compared the true effect size β and the estimated parameter value in each simulated dataset to evaluate the precision of PopCluster.
To compare the performance of PopCluster with the traditional analysis, we also analyzed each simulated dataset using logistic regression adjusted for sex and the four principal components, and we calculated the proportion of associations found significant for each of the parameters combinations. Note that each significant association found with the traditional analysis is a TP association in the subpopulation in which we simulated a true association, but a FP association in the remaining subset.
In the second scenario, we simulated an allele A to be associated with EL in the whole dataset using the probabilities P1 and P2 [Equation (5)]. We conducted this analysis to compare the TPR of PopCluster and the traditional analysis when there is no heterogeneity in the association between the SNP and the phenotype in different clusters. To evaluate PopCluster’s performance, we calculated the proportion of times PopCluster returned exactly one top cluster, and how often this cluster was identified as significant. In addition, for the rest of the results, when PopCluster returned more than one cluster, we calculated the average proportion of the clusters that were identified as significant. We calculated the TPR of the traditional analysis as the proportion of significant associations detected in the simulated datasets.
3 Results
3.1 Evaluation results
3.1.1 FPR
Figure 4 summarizes the results of the FPR evaluation. Each simulation was run 1000 times. On average, the estimated FPR in all six different simulations was . This low FPR shows that the correction for multiple comparisons incorporated in Equation (4) is sufficient to bound the family-wise error rate by the level of significance used in the algorithm. For additional details on this evaluation, see Supplementary Table S1.
Fig. 4.
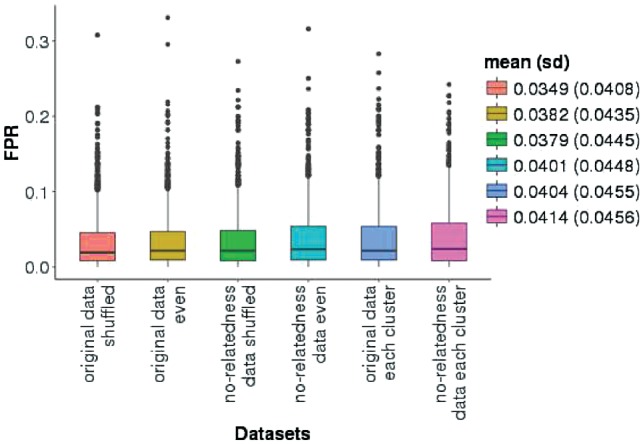
Boxplots of the FPR in six different simulations. Mean FPR and standard deviations (in parentheses) for each of the simulations are shown on the right of the Figure. ‘Original data shuffled’: original dataset with random reshuffling of cases and controls in a whole dataset. ‘Original data even’: original dataset with equal number of cases and controls randomly generated. ‘No-relatedness data shuffled’: as ‘original data shuffled’ after we removed related individuals. ‘No-relatedness data even’: as ‘original data even’ after we removed related individuals. ‘Original data each cluster’: original dataset with random reshuffling of cases and controls in each cluster. ‘No-relatedness data each cluster’: as ‘original data each cluster’ after we removed related individuals
We also evaluated the FPR of PopCluster on a homogeneous subset of our data—LGP (Table 1). We did this to verify the FPR when there are no clusters in the study populations. In 100% of simulations, PopCluster returned one cluster—the whole LGP dataset—as a final result, and the FPR in this case is equivalent to the FPR of a traditional analysis that adjust for the population structure. On average, the estimated FPR in this evaluation was .
3.1.2 TPR
The boxplots in Figure 5 summarize the results of the evaluation of the PopCluster’s TPR for all the combinations of probabilities of allele A in cases and controls when allele A was simulated to be associated with phenotype only in selected region (scenario 1). For each combination of parameters, simulations were run 1000 times. The percent of simulation runs that returned at least one cluster with more than 80% subjects in the region of association was 97.6% (Supplementary Table S2), and the average number of these ‘true association’ clusters was 2.6 (Supplementary Table S3). The TPR of PopCluster increases with the increase in difference in allele frequencies between cases and controls. High TPR values in the simulations with larger differences in allele frequencies suggest that the algorithm can detect clusters of significant association. Low TPR values for smaller differences in allele frequencies indicate that the dataset does not have enough power to detect those fine associations. In addition, we find that the differences between true effect size β and estimated are symmetrically distributed around 0 as expected (Supplementary Fig. S2). The black circles with white centers on boxplots in Figure 5 depict the proportion of general associations found by the traditional analysis. These proportions are comparable to the TPR of PopCluster; however they represent only TPR for finding a general association, but every TP in this case is a FP for a group of subjects in which allele A was simulated not to be associated with a phenotype.
Fig. 5.
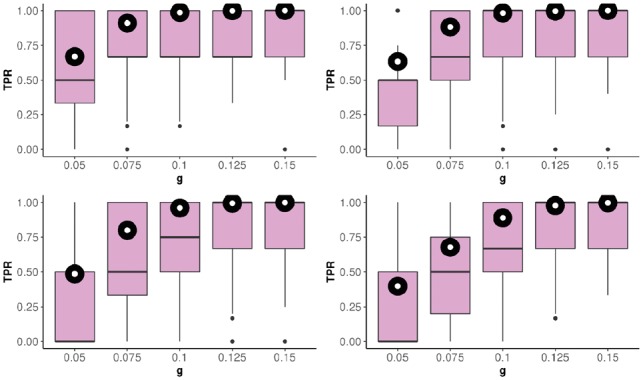
Boxplots of the TPR for various combinations of probabilities of allele A in cases and controls. g is the difference in allele probabilities between cases and controls. P(A) denotes the probability of allele A in cases. (A): . (B): . (C): . (D): . Black circles with white centers represent how often the traditional analysis finds a general association to be significant
The average TPR of the traditional analysis in datasets simulated to have an association between allele A and phenotype in the whole dataset (scenario 2) was 100%, meaning all of the runs returned an association as significant. The average number of times PopCluster returned only one cluster as a result was 30% (Supplementary Table S4). Among those single clusters, 100% of them were found to have a significant association between the simulated allele and phenotype. For the simulation runs that returned more than one cluster as a result, the average number of clusters that were found significant was 58%. We evaluated PopCluster’s performance in the case of allele–phenotype association simulated in the whole dataset in three more additional simulation set-ups that are presented in Supplementary Tables S5–S7.
3.2 Application to real data
We used PopCluster to re-analyze the association of the set of 371 SNPs with EL in the data summarized in Table 1. We assessed whether the algorithm could detect more significant associations than the analysis that adjusts for population structure, and identify sub-populations in which the associations were not significant. The analysis identified 14 SNPs in the APOE region that reached genome-wide level of significance in at least one cluster and although none of these cluster-specific associations was more significant than the results in the meta-analysis in Sebastiani et al. (2017b), the analysis suggests that the effect of APOE on EL may vary with ethnicity. In addition, PopCluster identified a large cluster of 7401 subjects in which the association between SNP rs2008465 (Table 2) and EL was more significant than in the meta-analysis, and smaller clusters comprising mainly North East Europeans in which the association between rs2008465 and EL was not significant. For complete results returned by PopCluster on the analysis of 371 SNPs and EL see Supplementary Table S9 and Figures S3–S12. To interpret ethnic groups from PCA plots, please refer to Supplementary Figure S13.
Below we present an example of SNP, rs3764814, with ethnic-specific effect on EL in sub-populations of Europeans. It also appeared to have an ethnic-specific effect on surviving past age 90 in the HRS dataset. To account for the varying sample sizes of clusters, we computed the power to detect significant associations in clusters using the G*Power software (Faul et al., 2009).
3.2.1 rs3764814 and EL
This SNP is a coding SNP in the gene USP42 which is located on chromosome 7. We recently found this SNP to be very strongly associated with EL in Europeans ignoring population-specific effects (Sebastiani et al., 2017b). The global MAF of rs3764814 is 0.28, but it becomes much rarer in Europeans: 0.07. The MAF of rs3764814 in our dataset is 0.09 and it increases 1.5 times in centenarians as compared to controls: 0.12 in cases and 0.08 in controls. Table 3 summarizes the results of PopCluster analysis for rs3764814 on EL. Supplementary Figure S14 presents a hierarchical tree of this dataset with the clusters returned for this SNP as highlighted in yellow [visualized with Cytoscape (Shannon et al., 2003)]. PopCluster identified two clusters (clusters 249 and 583 in Table 3 and black dots in Fig. 6) in which the association of rs3764814 did not reach statistical significance. Since clusters 249 and 583 are not sibling clusters, we can only conclude that there is no significant association of rs3764814 and EL in these two groups. Note that this is different than saying the effects are the same. In Figure 6, the highlighted subjects belong to clusters for which the association between SNP rs3764814 and EL is significant or borderline significant. Using partially known information on subjects’ ancestry, such as birth places and native languages of grandparents (Solovieff et al., 2010), we identified the subjects without an association as being enriched of Danish descent(Sebastiani et al., 2017a).
Table 3.
Complete list of clusters for rs3764814 and EL
| Cluster | OR | 95% CI | P-value | MAF | Power, % |
|---|---|---|---|---|---|
| 828 | 2.24 | [1.49, 3.36] | 9.87E-05 | 0.086 | 100 |
| 316 (583) | 2.89 | [1.61, 5.17] | 0.0004 | 0.085 | 100 |
| 721 | 1.91 | [1.31, 2.79] | 0.0007 | 0.093 | 100 |
| 805 (2971) | 2.22 | [1.37, 3.60] | 0.001 | 0.088 | 100 |
| 611 | 2.03 | [1.23, 3.35] | 0.006 | 0.075 | 100 |
| 2971 (805) | 1.3 | [1.07, 1.57] | 0.009 | 0.089 | 100 |
| 1145 | 1.47 | [1.08, 1.99] | 0.01 | 0.105 | 100 |
| 126 | 3.75 | [1.28, 11.00] | 0.02 | 0.075 | 100 |
| 606 | 1.61 | [1.07, 2.42] | 0.02 | 0.094 | 100 |
| 249 | 1.3 | [0.63, 2.71] | 0.48 | 0.064 | 50 |
| 583 (316) | 0.85 | [0.49, 1.49] | 0.57 | 0.071 | 47 |
Note: Cluster: label for the cluster which reflect cluster size, e.g. cluster labeled 583 consists of 583 subjects (if in the final dendrogram structure, a cluster has a sibling, it is reported here in parentheses).
OR: odds ratio for EL in carriers of the allele; 95% CI: 95% confidence interval for the OR; P-value: P-value of the association; MAF: minor allele frequency in the cluster; Power, %: power of detecting a given OR with a given number of subjects.
Fig. 6.
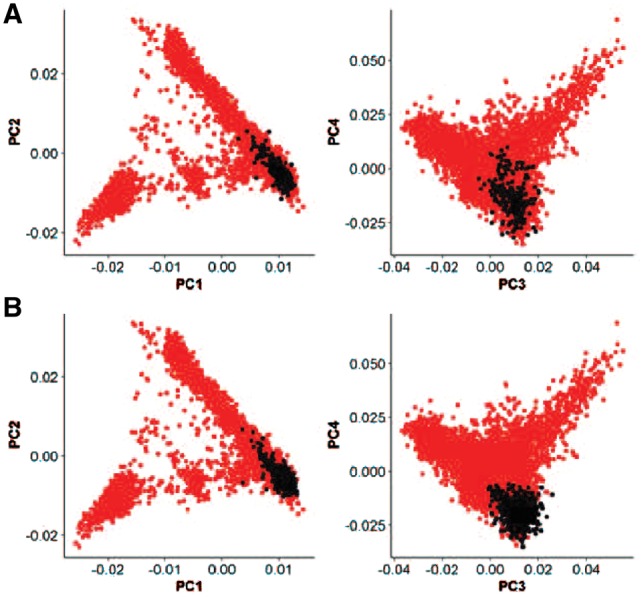
Ethnic groups in which the effects of SNP rs3764814 on EL did not reach statistical significance. The scatter plots display the principal components PC1-PC4 calculated using genome-wide genotype data of all subjects in the study of EL. Subjects colored in black belong to (Panel A): cluster 249, (Panel B): cluster 583 as defined in Table 3
3.2.2 rs72834698 and survival past age 90
We used PopCluster to analyze the association between SNP rs72834698 and surviving past the age of 90 in the HRS dataset. The analysis identified one large cluster of 8128 subjects in which this SNP had a significant association with survival past age 90 (cluster 8128 in Table 4 and highlighted subjects in Fig. 7). Note that this association is not significant after correction for multiple testing. Based on self-reported ethnicity labels provided with HRS dataset, the group of subjects that is not in this cluster (black dots in Fig. 7) is enriched of ‘Hispanic, Mexican’ subjects. Supplementary Figure S15 presents a hierarchical tree with clusters returned for rs72834698 in yellow. For more results on this analysis, see Supplementary Table S8 and Figure S16.
Table 4.
Complete list of clusters for rs72834698 returned as an output from PopCluster run on HRS dataset with phenotype of surviving past age 90
| Cluster | OR | 95% CI | P-value | MAF | Power, % |
|---|---|---|---|---|---|
| 8128 (236) | 1.26 | [1.06, 1.50] | 0.008 | 0.098 | 100 |
| 236 (8128) | 0.34 | [0.10, 1.16] | 0.09 | 0.083 | 100 |
| 811 | 0.64 | [0.31, 1.28] | 0.21 | 0.075 | 100 |
| 160 | 1.01 | [0.50, 2.01] | 0.99 | 0.181 | 5 |
Fig. 7.
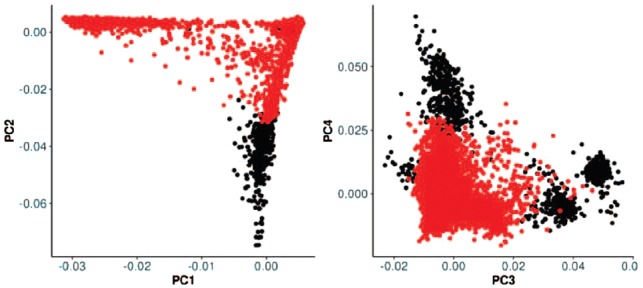
The scatter plots display the principal components PC1-PC4 calculated using genome-wide genotype data of all subjects in HRS study. Highlighted subjects are the 8128 subjects from the cluster that is defined in Table 4
4 Discussion
Currently most of the genetics studies are based on data generated in subjects of specific European ancestry, and sometimes the results of the genetic association studies do not generalize to other populations (Martin et al., 2017). The issue of underrepresentation of non-European populations in genetic studies is slowly being addressed (Popejoy and Fullerton, 2016); and it is important to adapt current techniques to account for the different allele frequencies and genetic effects in those populations. There are methods that have been proposed to account for the heterogeneity of variants and phenotype associations in different populations. For example, the generalized linear mixed model association test accounts for population stratification and varying binary phenotype frequencies in different populations (Chen et al., 2016). The generalized linear mixed model association test corrects P-values and effect estimates in the genetic association studies in the presence of non-constant mean-variance relationship for a binary phenotype; however, it does not identify the varying effect sizes in the populations. Another approach, XP-BLUP, predicts individual genetic risk scores for heterogeneous subjects by incorporating multi- and trans-ethnic information in the analysis (Coram et al., 2017). The novelty of PopCluster is to provide a heuristic search to discover heterogeneous effects when the sub-populations are unknown.
There are many consequences of not being able to identify the varying genetic effects in the studies that consist of only or a majority of European samples. This problem is particularly important in genetic association studies that aim to discover new drug targets. Currently there are several high-selling medications that do not help or even hurt the majority of people who take them (Schork, 2015). Another area that would benefit the delineation of population-specific genetic effects is genetic risk prediction. When a genetic marker for a trait is identified using predominantly European populations, using this marker for prediction of disease risk in non-Europeans may result in a higher FP diagnostic rate (Manrai et al., 2016; The PLOS Medicine Editors et al., 2016).
Various factors, such as genetics, diet, lifestyle and endemic infectious diseases, contribute to varying allele frequencies and genetic effects in different populations (Kelly et al., 2017; Petrovski and Goldstein, 2016; Rosenberg et al., 2002). In addition, different genetic markers can be associated with the same disease phenotype in different populations (Schork, 1997). PopCluster performs the association studies in populations with varying genetic effects on a phenotype to account for the diverse ancestry and environmental backgrounds.
PopCluster can also be used as a step before performing meta-analysis when working with multi- and trans-ethnic studies. The algorithm facilitates identification of populations with heterogeneous genetic effects. Subsequently, separate GWAS can be performed on the detected sub-populations, and the results can be combined using tools such as trans-ethnic meta-analysis (Morris, 2011).
In the evaluation we tested datasets with a small number of related individuals (∼14%) and the algorithm worked well in those cases. However, when the number of related individuals is large, proper corrections for relatedness are important. In our implementation of the algorithm, we use the R geeglm function from the geepack package (Hojsgaard et al., 2006) to fit the regression model. If the dataset includes related individuals, PopCluster can use a generalized estimating equation to adjust for within-family correlation (Wang et al., 2013). In our examples we only used a binary phenotype. However, in the implementation of PopCluster, there is an option to choose the probability distribution of the outcome in the regression model so the algorithm can be used to analyze continuous phenotypes.
PopCluster has several limitations that we outline below. One of the limitations of our algorithm is that even though it finds ethnicity-specific associations that otherwise would have been missed, breaking the dataset into smaller clusters makes the association testing less powerful. Additionally, if the initial dataset has a small number of samples that belong to genetically very different group compared to the rest of the samples, PopCluster might not be able to identify the presence of ethnicity-dependent effects as it would not process clusters below the root node of the dendrogram (Fig. 1). In such situation, we recommend to remove these distinct samples from the dataset, and re-run PopCluster on the updated set of samples. In situations when genetic variants do not have heterogeneous associations with a phenotype in different populations, PopCluster might lead to overfitting and identify differential associations between clusters. Thus, it is important to have a replication for all the findings. Another constraint is that PopCluster accepts the data with quality control performed beforehand. For example, systematic differences in genotyping of the data could bias the PCA. In our examples, we performed quality control on genome-wide genotype data so that highly polymorphic regions and SNPs in high LD are removed, and that the strand direction is consistent for all the studies, etc. However, some additional sources of bias may always be possible and it might be useful to verify that the clusters represent ethnical differences if appropriate label data for some of the subjects are known. In our examples, we verified that the clusters represent European ethnicities using subjects and their parents’ places of birth, or mother tongue. This step is not necessary, but it is an addition to validating the results.
PopCluster could be extended in a few different ways. For example, we applied hierarchical clustering to identify different populations because of its deterministic nature; however, other clustering approaches could be used in a similar manner on a set of principal components inferred from the genome-wide genetics data (Solovieff et al., 2010). The current implementation of PopCluster is not designed to analyze genome-wide genotype data and can be used to re-analyze the associations between the SNPs that reach a certain level of significance in a standard GWAS. For future work, we would like to optimize the implementation of PopCluster to become applicable to big genetic data and apply PopCluster to large datasets with various populations and to test it in regards to different phenotypes. We are hopeful that the use of the PopCluster’s methodology will contribute to more precise estimate of genetic associations in the presence of population heterogeneity and ultimately better use of genetic findings in precision medicine.
Funding
This work was supported by the National Institute on Aging [U01AG023755, U19AG023122, R21AG056630]; the William M. Wood Foundation; the Paulette and Marty Samowitz Family Foundation; the Longevity Genes Project [R01AG618381, R01AG042188, R01AG046949, P01AG021654]; the Einstein Nathan Shock Center grant [P30AG038072]; and the Einstein Glenn Center for the Biology of Human Aging. The Health and Retirement Study genetic data are sponsored by the National Institute on Aging [U01AG009740, RC2AG036495, RC4AG039029] and was conducted by the University of Michigan.
Conflict of Interest: none declared.
Supplementary Material
References
- Andersen S.L., et al. (2012) Health span approximates life span among many supercentenarians: compression of morbidity at the approximate limit of life span. J. Gerontol. A Biol. Sci. Med. Sci., 67A, 395–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atzmon G., et al. (2004) Clinical phenotype of families with longevity. J. Am. Geriatr. Soc., 52, 274–277. [DOI] [PubMed] [Google Scholar]
- Bell F., Miller M. (2005) Life tables for the United States Social Security area 1900–2100. Actuarial Study, 116, 2005. SSA Pub. No. 120. SSA Pub. No. 11–11536. [Google Scholar]
- Campos M., et al. (2013) An exploratory study of APOE-e4 genotype and risk of Alzheimer’s disease in Mexican Hispanics. J. Am. Geriatr. Soc., 61, 1038–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlson C.S., et al. (2013) Generalization and dilution of association results from European GWAS in populations of non-European ancestry: the PAGE study. PLoS Biol., 11, e1001661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H., et al. (2016) Control for population structure and relatedness for binary traits in genetic association studies via logistic mixed models. Am. J. Hum. Genet., 98, 653–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cingolani P., et al. (2012) A program for annotating and predicting the effects of single nucleotide polymorphisms, SnpEff: SNPs in the genome of Drosophila melanogaster strain w1118; iso-2; iso-3. Fly, 6, 80–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coram M.A., et al. (2017) Leveraging multi-ethnic evidence for risk assessment of quantitative traits in minority populations. Am. J. Hum. Genet., 101, 218–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbo R.M., Scacchi R. (1999) Apolipoprotein E (APOE) allele distribution in the world. Is APOE*4 a ‘thrifty’ allele? Ann. Hum. Genet., 9, 301–310. [DOI] [PubMed] [Google Scholar]
- Faul F., et al. (2009) Statistical power analyses using G*Power 3.1: tests for correlation and regression analyses. Behav. Res. Methods, 41, 1149–1160. [DOI] [PubMed] [Google Scholar]
- Hendrie H.C., et al. (2014) APOE e4 and the risk for Alzheimer disease and cognitive decline in African Americans and Yoruba. Int. Psychogeriatr., 26, 977–985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hojsgaard S., et al. (2006) The R Package geepack for Generalized Estimating Equations. J. Stat. Softw., 15, 1–11. [Google Scholar]
- Howie B., et al. (2012) Fast and accurate genotype imputation in genome-wide association studies through pre-phasing. Nat. Genet., 44, 955–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly D.E., et al. (2017) Global variation in gene expression and the value of diverse sampling. Curr. Opin. Syst. Biol., 1, 102–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C.-C., et al. (2013) Apolipoprotein E and Alzheimer disease: risk, mechanisms, and therapy. Nat. Rev. Neurol., 9, 106–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malovini A., et al. (2011) Association study on long-living individuals from Southern Italy identifies rs10491334 in the CAMKIV gene that regulates survival proteins. Rejuvenation Res., 14, 283–291. [DOI] [PubMed] [Google Scholar]
- Manrai A.K., et al. (2016) Genetic misdiagnoses and the potential for health disparities. N. Engl. J. Med., 375, 655–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin A.R., et al. (2017) Human demographic history impacts genetic risk prediction across diverse populations. Am. J. Hum. Genet., 100, 635–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathew S.S., et al. (2017) Inclusion of diverse populations in genomic research and health services: genomix workshop report. J. Community Genet., 8, 267–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris A.P. (2011) Transethnic meta-analysis of genomewide association studies. Genet. Epidemiol., 35, 809–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Need A.C., Goldstein D.B. (2009) Next generation disparities in human genomics: concerns and remedies. Trends Genet., 25, 489–494. [DOI] [PubMed] [Google Scholar]
- Newman A.B., et al. (2011) Health and function of participants in the Long Life Family Study: a comparison with other cohorts. Aging, 3, 63–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrovski S., Goldstein D.B. (2016) Unequal representation of genetic variation across ancestry groups creates healthcare inequality in the application of precision medicine. Genome Biol., 17, 157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popejoy A.B., Fullerton S.M. (2016) Genomics is failing on diversity. Nature, 538, 161–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price A.L., et al. (2006) Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet., 38, 904–909. [DOI] [PubMed] [Google Scholar]
- Rosenberg N.A., et al. (2002) Genetic structure of human populations. Science, 298, 2381–2385. [DOI] [PubMed] [Google Scholar]
- Schork N.J. (1997) Genetics of complex disease: approaches, problems, and solutions. Am. J. Respir. Crit. Care Med., 156, S103–S109. [DOI] [PubMed] [Google Scholar]
- Schork N.J. (2015) Personalized medicine: time for one-person trials. Nature, 520, 609–611. [DOI] [PubMed] [Google Scholar]
- Sebastiani P., Perls T.T. (2012) The genetics of extreme longevity: lessons from the New England Centenarian Study. Front. Genet., 3, 277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebastiani P., et al. (2012) Genetic signatures of exceptional longevity in humans. PLoS One, 7, 1–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebastiani P., et al. (2016a) Familial risk for exceptional longevity. N. Am. Actuar. J., 20, 57–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebastiani P., et al. (2016b) Increasing sibling relative risk of survival to older and older ages and the importance of precise definitions of “aging” “life span”, and “longevity”. J. Gerontol. A Biol. Sci. Med. Sci., 71, 340–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebastiani P., et al. (2017a) Assortative mating by ethnicity in longevous families. Front. Genet., 8, 186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebastiani P., et al. (2017b) Four genome-wide association studies identify new extreme longevity variants. J. Gerontol. A Biol. Sci. Med. Sci., 72, 1453–1464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebastiani P., et al. (2017c) Limitations and risks of meta-analyses of longevity studies. Mech. Ageing Dev., 165, 139–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon P., et al. (2003) Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res., 13, 2498–2504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solovieff N., et al. (2010) Clustering by genetic ancestry using genome-wide SNP data. BMC Genetics, 11, 108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonnega A., et al. (2014) Cohort Profile: the Health and Retirement Study (HRS). Int. J. Epidemiol., 43, 576–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The PLOS Medicine Editors et al (2016) Towards equity in health: researchers take stock. PLoS Med., 13, e1002186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torkamani A., et al. (2012) Clinical implications of human population differences in genome-wide rates of functional genotypes. Front. Genet., 3, 211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., et al. (2013) GEE-based SNP set association test for continuous and discrete traits in family-based association studies. Genet. Epidemiol., 37, 778–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


