Abstract
Optimal superposition of protein structures or other biological molecules is crucial for understanding their structure, function, dynamics and evolution. Here, we investigate the use of probabilistic programming to superimpose protein structures guided by a Bayesian model. Our model THESEUS-PP is based on the THESEUS model, a probabilistic model of protein superposition based on rotation, translation and perturbation of an underlying, latent mean structure. The model was implemented in the probabilistic programming language Pyro. Unlike conventional methods that minimize the sum of the squared distances, THESEUS takes into account correlated atom positions and heteroscedasticity (ie. atom positions can feature different variances). THESEUS performs maximum likelihood estimation using iterative expectation-maximization. In contrast, THESEUS-PP allows automated maximum a-posteriori (MAP) estimation using suitable priors over rotation, translation, variances and latent mean structure. The results indicate that probabilistic programming is a powerful new paradigm for the formulation of Bayesian probabilistic models concerning biomolecular structure. Specifically, we envision the use of the THESEUS-PP model as a suitable error model or likelihood in Bayesian protein structure prediction using deep probabilistic programming.
Index Terms—: protein superposition, Bayesian modelling, deep probabilistic programming, protein structure prediction
I. Introduction
In order to compare biomolecular structures, it is typically necessary to superimpose them onto each other in an optimal way. The standard method minimizes the sum of the squared distances (root mean square deviation, RMSD) between the matching atom pairs. This can be easily accomplished by shifting the centre of mass of the two proteins to the origin and obtaining the optimal rotation using singular value decomposition [1] or quaternion algebra [2], [3]. These methods however typically assume that all atoms have equal variance (heteroscedasticity) and are uncorrelated. This is potentially problematic, for example in the case of proteins with flexible loops or flexible terminal regions, which correspond to atoms positions with high variance. Here we present a Bayesian model that is based on the previously reported THESEUS model [4], [5]. The THESEUS model is a probabilistic model of protein superposition that allows for regions with low and high variance, corresponding respectively to conserved and variable regions [4], [5]. THESEUS assumes that the structures which are to be superimposed are translated, rotated and perturbed observations of an underlying latent, mean structure M.
In contrast to the THESEUS model which features maximum likelihood parameter estimation using iterative expectation maximization, we formulate a Bayesian model (THESEUS-PP) and perform maximum a-posteriori parameter estimation. We provide suitable prior distributions over the rotation, the translations, the variances and the latent, mean model. We implement the entire model in the probabilistic programming language Pyro [6], and make use of its automated inference features.
The results indicate that deep probabilistic programming readily allows the implementation, estimation and deployment of advanced non-Euclidean models relevant to structural bioinformatics. Specifically, we envision that THESEUS-PP can be adapted for use as a likelihood function in Bayesian protein structure prediction using deep probabilistic programming, due to its support for heteroscedasticity.
II. Methods
A. Overall model
According to the THESEUS model, each protein structure Xi is a noisy observation of a rotated and translated latent, mean structure M,
| (1) |
where Ri is a rotation matrix, ti is a three-dimensional translation and ϵi is the error. Another way of representing the model is seeing Xi as distributed according to a matrix-normal distribution with mean M and covariance matrices U and V - one concerning the rows and the other the columns.
The matrix-normal distribution can be considered as an extension of the standard multivariate normal distribution from vector-valued to matrix-valued random variables. Consider a random variable X distributed according to a matrix-normal distribution with mean M, which in our case is an N×3 matrix where N is the number of atoms. In this case, the matrix-normal distribution is further characterized by an N × N row covariance matrix U and a 3 × 3 column covariance V. Then, will be distributed according to
| (2) |
where Q is an N × 3 matrix with elements distributed according to the standard normal distribution.
To ensure identifiability, one (arbitrary) protein X1 is assumed to be a noisy observation of the translated - but not rotated - mean structure M:
| (3) |
The other protein X2 is assumed to be a noisy observation of the rotated as well as translated mean structure M:
| (4) |
Thus, the model uses the same covariance matrices U and V for the matrix-normal distributions of both X1 and X2.
B. Bayesian posterior
The graphical model of THESEUS-PP is shown in Figure 1. The corresponding Bayesian posterior distribution is
| (5) |
where I3 is the three-dimensional identity matrix. Below, we specify how each of the priors and the likelihood function is formulated and implemented.
Fig. 1:
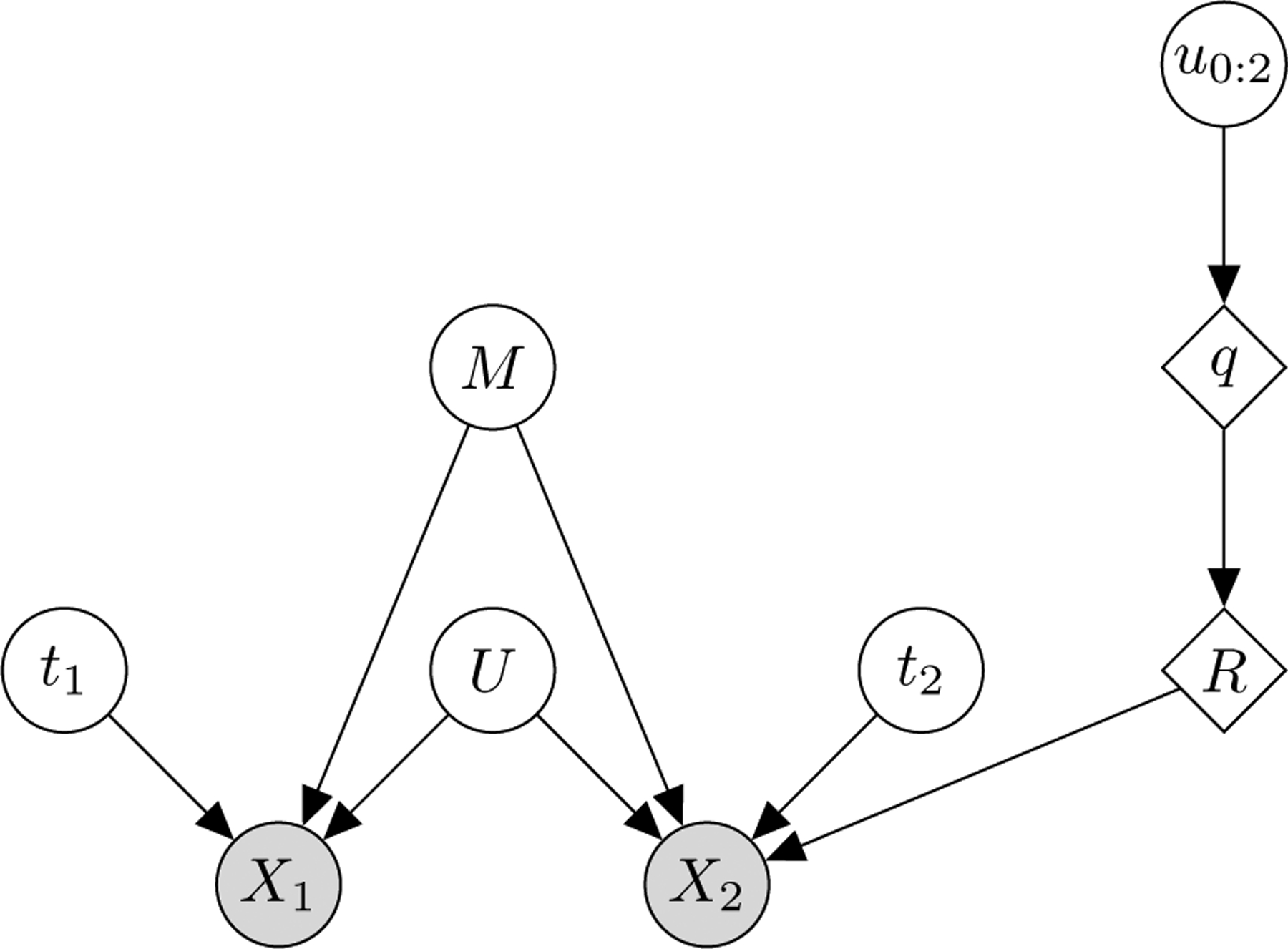
The THESEUS-PP model as a Bayesian graphical model. M is the latent, mean structure, which is an N-by-3 coordinate matrix, where N is the number of atoms. t1 and t2 are the translations. q is a unit quaternion calculated from three random variables u0:2 sampled from the unit interval and R is the corresponding rotation matrix. U is the among-row variance matrix of a matrix-normal distribution; X1 and X2 are N-by-3 coordinate matrices representing the proteins to be superimposed. Circles denote random variables; squares denote deterministic transformations of random variables. Shaded circles denote observed variables. Capital and small letters represent matrices and vectors respectively.
C. Prior for the mean structure M
Recall that according to the THESEUS-PP model, the atoms of the structures to be superimposed are noisy observations of a mean structure, M = {m0, …, mN−1}, where N is the number of atoms considered in the superposition. Typically, only Cα atoms are considered and in that case, N corresponds to the number of amino acids. Hence, we need to formulate a prior distribution over the latent, mean structure M. We use an uninformative prior for M. Each element of M is sampled from a univariate normal distribution with mean 0 and variance σM. We set σM to the maximum distance of a Cα atom to the center of its structure. Finally, M is translated so its center-of-mass lies at the origin.
D. Prior over the rotation R
In the general case, we have no a priori information on the optimal rotation. Hence, we use a uniform prior over the space of rotations. There are several ways to construct such a uniform prior. We have chosen a method that makes use of quaternions [7]. Quaternions are the 4-dimensional extensions of the better known 2-dimensional complex numbers. Unit quaternions form a convenient way to represent rotation matrices. For our goal, the overall idea is to sample uniformly from the space of unit quaternions. Subsequently, the sampled unit quaternions are transformed into the corresponding rotation matrices, which establishes a uniform prior over rotations.
A unit quaternion q = (w, x, y, z) is sampled in the following way. First, three independent random variables are sampled from the unit interval,
| (6) |
Then, four auxiliary deterministic variables (θ1, θ2, r1, r2) are calculated from u1, u2, u3,
| (4a) |
| (4b) |
| (4c) |
| (4d) |
The unit quaternion q is then obtained in the following way,
| (7) |
Finally, the unit quaternion q is transformed into its corresponding rotation matrix R as follows,
| (8) |
E. Prior over the translations t1 and t2
For the translations, we use a standard trivariate normal distribution,
| (9) |
where I3 is the identity matrix. This prior assumes that X1, X2 and M are centered at the origin before the translations are applied (see below).
F. Prior over U
The matrix-normal distribution has two covariance matrices, one concerning the rows (U) and another concerning the columns (V). V can be set to the identity matrix I3. The N diagonal elements of U are sampled from the half-normal distribution with standard deviation set to 0.01,
G. Likelihood
In our case, the matrix-normal likelihood can be formulated as a product of univariate normal distributions. Below, we have used trivariate Gaussian distributions with diagonal covariance matrices for ease of notation. The likelihood can thus be written as
| (10) |
where the product runs over the matrix rows that contain the x, y, z coordinates of X1, X2 and the rotated and translated latent, mean structure M.
H. Algorithm

I. Initialization
Convergence of the MAP estimation can be greatly improved by selecting suitable starting values for certain variables and by transforming the two structures in a suitable way. First, we superimpose the two structures using conventional least-squares superposition. Therefore, the starting rotation can be initialized close to the identity matrix (ie., no rotation). This is done by setting the vector u to (0.9,0.1,0.9).
Optimization can be further enhanced by initializing the mean structure M to the average of the two input structures X1 and X2.
J. Maximum a-posteriori optimization
We performed MAP estimation using Pyro’s AutoDelta guide. For optimization, we used AdagradRMSProp [8], [9] with the default parameters for the learning rate, momentum and step size modulator. For some proteins, optimization sometimes fails to converge due to numerical instabilities (data not shown). We are investigating means to reparameterise the model in order to avoid this.
Convergence was detected using Earlystop from Pytorch’s Ignite library (version 0.2.0) [10]. This method evaluates the stabilization of the error loss and stops the optimization according to the value of the patience parameter. The patience value was set to 100.
III. Materials
Proteins
The algorithm was tested on several proteins from the RCSB protein database [11] that were obtained from Nuclear Magnetic Resonance (NMR) experiments. Such structures typically contain several models of the same protein. These models represent the structural dynamics of the protein in an aqueous medium and thus typically contain both conserved and variable regions. This makes them challenging targets for conventional RMSD superposition. We used the following structures: 1ADZ, 1AHL, 1AK7, 2KHI and 2LKL.
IV. Results
The algorithm was executed 10 times on each protein (see Table I).
TABLE I:
Results of applying THESEUS-PP to the test structures. First column: PDB identifier. Second column: the number of Cα atoms used in the superposition. Third column: the model identifiers. Fourth column: mean convergence time and standard deviation. Last column: Number of iterations.
| PBD ID | Length (Amino Acids) | Protein Models | Average Computational Time (seconds) | Iterations |
|---|---|---|---|---|
| 1ADZ | 71 | 0 and 1 | 3.3 ± 0.95 | 663 ±121 |
| 1AHL | 49 | 0 and 2 | 3.75± 0.42 | 626 ±59 |
| 1AK7 | 174 | 0 and 1 | 4.2± 0.35 | 626 ±109 |
| 2KHI | 95 | 0 and 1 | 8.95±9.59 | 952±1121 |
| 2LKL | 81 | 0 and 8 | 8.05± 7.13 | 1403±1354 |
The resulting superimposed structures are shown in Figure 2. For comparison, conventional RMSD superpositions, obtained using Biopython [12], are shown on the left. THESEUS-PP superpositions are shown on the right. Note how the former fail to adequately distinguish regions with high from regions with low variance, resulting in poor matching of conserved regions.
Fig. 2:
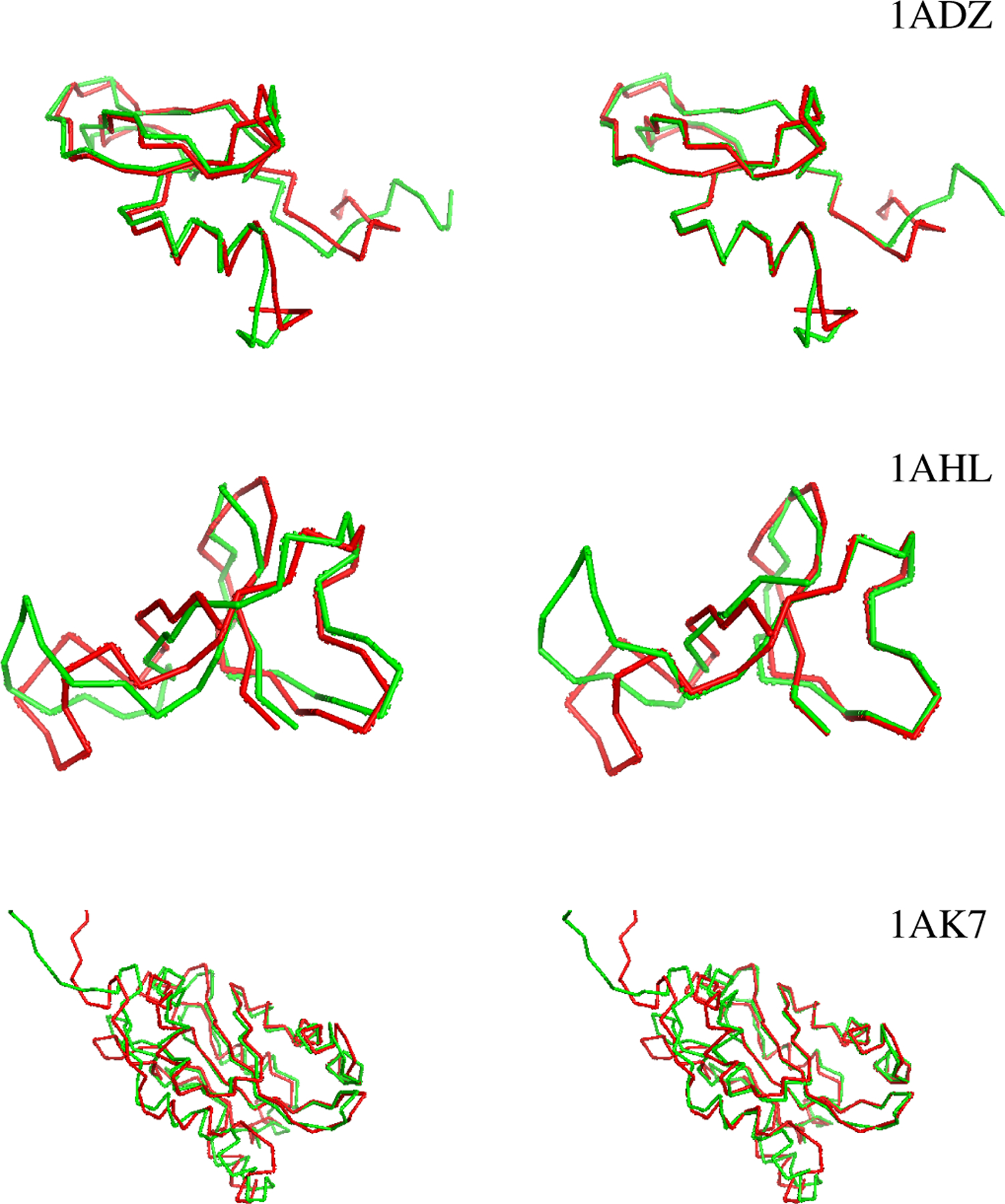
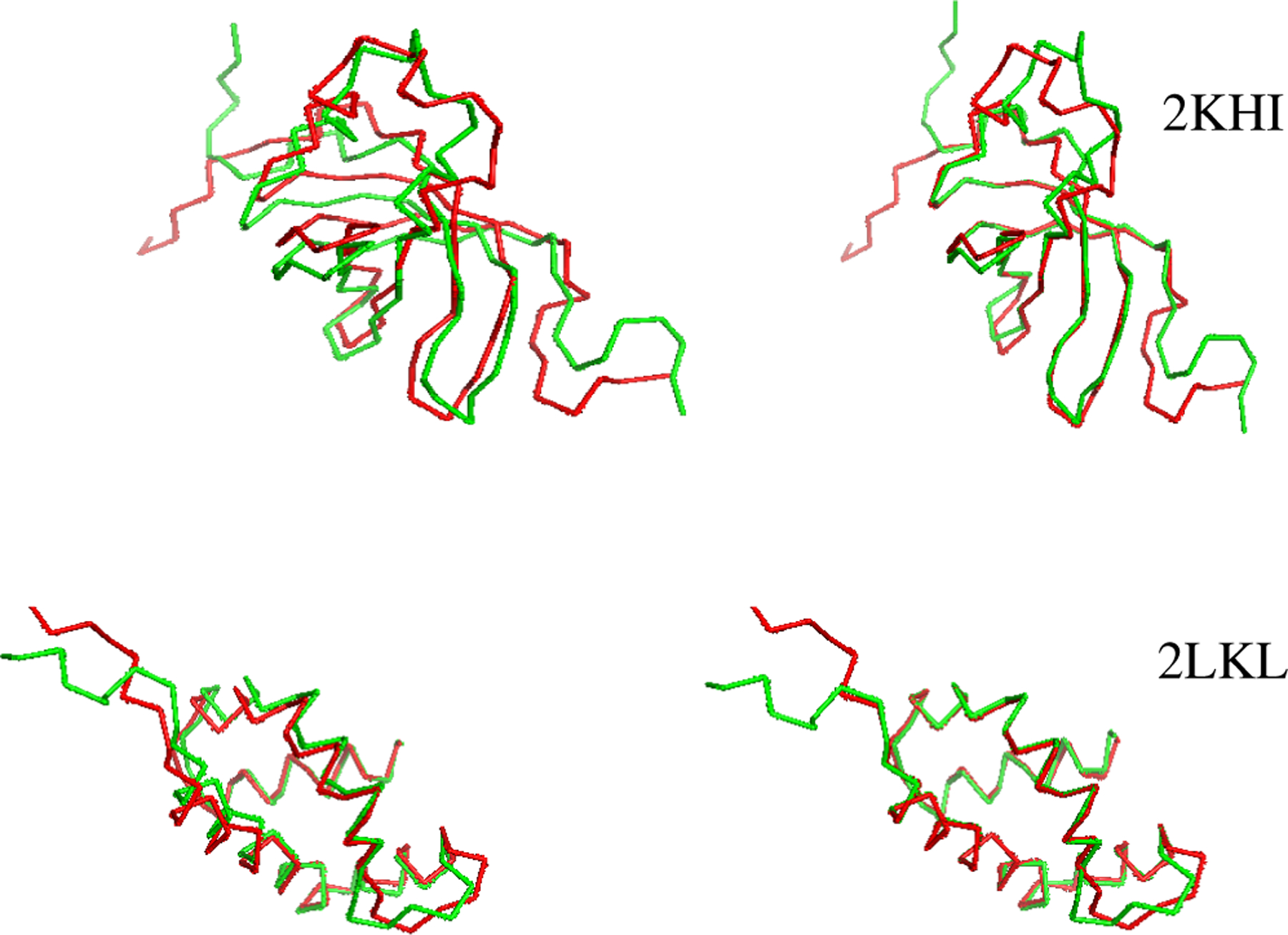
Protein pairs obtained with conventional RMSD superimposition (left) and with THESEUS-PP (right).The protein in green is rotated (X2). The images are generated with PyMOL [13].
V. Conclusion
Probabilistic programming is a powerful, emerging paradigm for probabilistic protein structure analysis, prediction and design. Here, we present a Bayesian model for protein structure superposition implemented in the deep probabilistic programming language Pyro and building on the previously reported THESEUS maximum likelihood model. MAP estimates of its parameters are readily obtained using Pyro’s automated inference engine. Recently, end-to-end protein protein structure prediction using deep learning methods has become possible [14]. We envision that Bayesian protein structure prediction will soon be possible using a deep probabilistic programming approach, which will lead to protein structure predictions with associated statistical uncertainties. In order to achieve this goal, suitable error models and likelihood functions need to be developed and incorporated in these models. The THESEUS-PP model can potentially serve as such an error model, by interpreting M as the predicted structure and a single rotated and translated X as the observed protein structure. During training of the probabilistic model, regions in M that are wrongly predicted can be assigned high variance, while correctly predicted regions can be assigned low variance. Thus, it can be expected that an error model based on THESEUS-PP will make estimation of these models easier, as the error function can more readily distinguish between partly correct and entirely wrong predictions, which is notoriously difficult for RMSD-based methods [15].
Fig. 3:
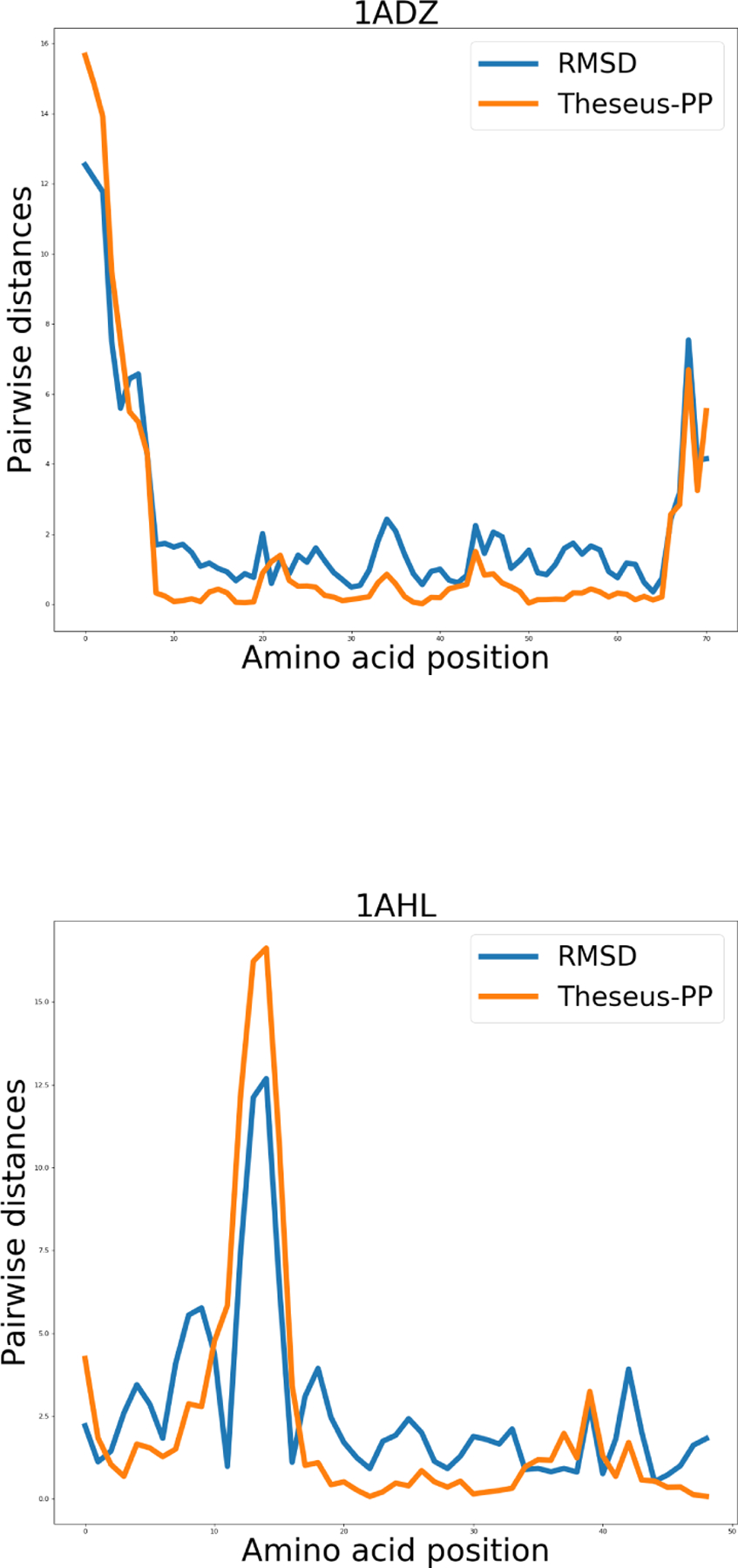
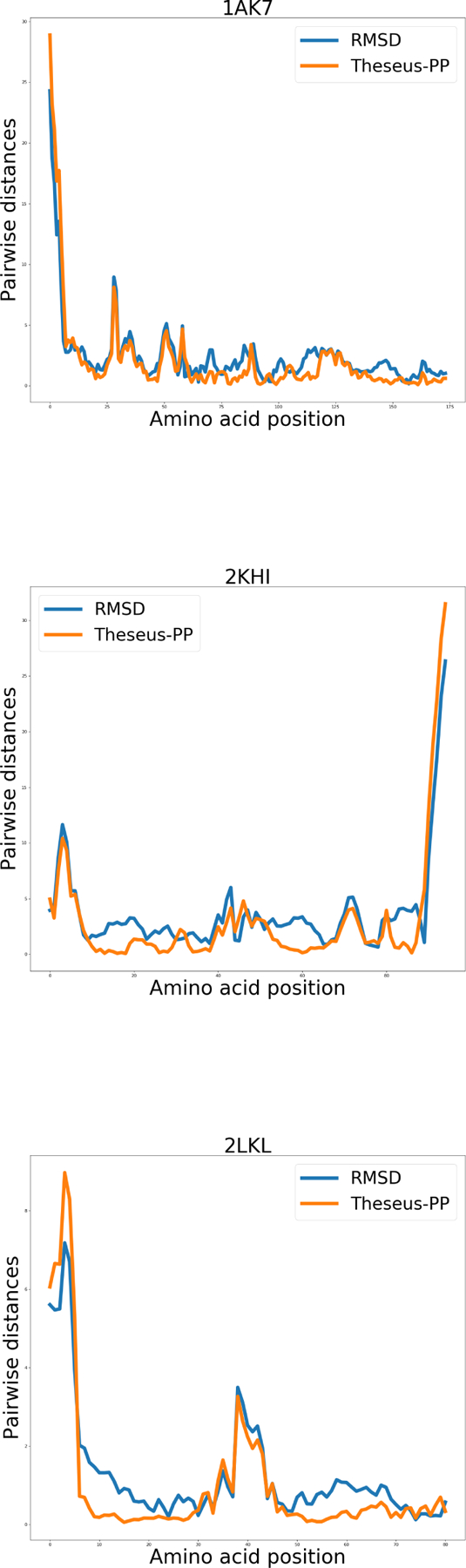
Graphs showing the pairwise distances (in Å) between the Cα coordinates of the structure pairs. The blue and orange lines represent RMSD and THESEUS-PP superposition, respectively.
Contributions and Acknowledgements
Implemented algorithm in Pyro: LSM. Contributed code: ASA, AM. Wrote article: LSM, TH, ASA. Prototyped algorithm in pyMC3: TH, WB, BNR. Performed experiments: LSM. Designed experiments: TH, DT. LSM and ASA acknowledge funding from the Independent Research Fund Denmark (DFF-FTP) and Innovationsfonden, respectively.
References
- [1].Kabsch W, “A discussion of the solution for the best rotation to relate two sets of vectors,” Acta Cryst. A, vol. 34, pp. 827–828, 1978. [Google Scholar]
- [2].Horn B, “Closed-form solution of absolute orientation using unit quaternions,” J. Opt. Soc. Am. A, vol. 4, pp. 629–642, 1987. [Google Scholar]
- [3].Coutsias E, Seok C, and Dill K, “Using quaternions to calculate rmsd,” J. Comp. Chem, vol. 25, pp. 1849–1857, 2004. [DOI] [PubMed] [Google Scholar]
- [4].Theobald DL and Wuttke DS, “Empirical Bayes hierarchical models for regularizing maximum likelihood estimation in the matrix Gaussian Procrustes problem,” PNAS, vol. 103, pp. 18521–18527, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Theobald DL and Steindel PA, “Optimal simultaneous superpositioning of multiple structures with missing data,” Bioinformatics, vol. 28, pp. 1972–1979, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Bingham E, Chen JP, Jankowiak M, Obermeyer F, Pradhan N, Karaletsos T, Singh R, Szerlip P, Horsfall P, and Goodman ND, “Pyro: Deep Universal Probabilistic Programming,” Journal of Machine Learning Research, 2018. [Google Scholar]
- [7].Perez-Sala X, Igual L, Escalera S, and Angulo C, “Uniform sampling of rotations for discrete and continuous learning of 2D shape models,” in Robotic Vision: Technologies for Machine Learning and Vision Applications. IGI Global, 2013, pp. 23–42. [Google Scholar]
- [8].Duchi J, Hazan E, and Singer Y, “Adaptive subgradient methods for online learning and stochastic optimization,” Journal of Machine Learning Research, vol. 12, no. July, pp. 2121–2159, 2011. [Google Scholar]
- [9].Graves A, “Generating sequences with recurrent neural networks,” arXiv preprint arXiv:1308.0850, 2013. [Google Scholar]
- [10].Paszke A, Gross S, Chintala S, Chanan G, Yang E, DeVito Z, Lin Z, Desmaison A, Antiga L, and Lerer A, “Automatic differentiation in pytorch,” in NIPS-W, 2017. [Google Scholar]
- [11].Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, and Bourne PE, “The protein data bank,” Nucleic acids research, vol. 28, no. 1, pp. 235–242, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Cock PJ, Antao T, Chang JT, Chapman BA, Cox CJ, Dalke A, Friedberg I, Hamelryck T, Kauff F, Wilczynski B et al. , “Biopython: freely available python tools for computational molecular biology and bioinformatics,” Bioinformatics, vol. 25, no. 11, pp. 1422–1423, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Schrödinger LLC, “The PyMOL molecular graphics system, version 1.8,” November 2015.
- [14].AlQuraishi M, “End-to-end differentiable learning of protein structure,” Available at SSRN; 3239970, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Kufareva I and Abagyan R, “Methods of protein structure comparison,” in Homology Modeling. Springer, 2011, pp. 231–257. [DOI] [PMC free article] [PubMed] [Google Scholar]


