Abstract
Cardiac Cine Magnetic Resonance (CMR) Imaging has made a significant paradigm shift in medical imaging technology, thanks to its capability of acquiring high spatial and temporal resolution images of different structures within the heart that can be used for reconstructing patient-specific ventricular computational models. In this work, we describe the development of dynamic patient-specific right ventricle (RV) models associated with normal subjects and abnormal RV patients to be subsequently used to assess RV function based on motion and kinematic analysis. We first constructed static RV models using segmentation masks of cardiac chambers generated from our accurate, memory-efficient deep neural architecture – CondenseUNet – featuring both a learned group structure and a regularized weight-pruner to estimate the motion of the right ventricle. In our study, we use a deep learning-based deformable network that takes 3D input volumes and outputs a motion field which is then used to generate isosurface meshes of the cardiac geometry at all cardiac frames by propagating the end-diastole (ED) isosurface mesh using the reconstructed motion field. The proposed model was trained and tested on the Automated Cardiac Diagnosis Challenge (ACDC) dataset featuring 150 cine cardiac MRI patient datasets. The isosurface meshes generated using the proposed pipeline were compared to those obtained using motion propagation via traditional non-rigid registration based on several performance metrics, including Dice score and mean absolute distance (MAD).
Index Terms—: Condensation-optimization network, right ventricle segmentation and propagation, image registration, displacement field reconstruction, patient-specific modeling
I. INTRODUCTION
According to the recent report from the American Heart Association, one-third of all deaths in the U.S. are caused by cardiovascular diseases (CVDs), some associated with compromised function of the right ventricle [1]. Important examples of such heart diseases include right ventricle (RV) ischemia and hypertrophy which may lead to abnormal RV motion. An efficient method that can accurately estimate the motion of the RV from cardiac images with the overall goal to study the RV kinematics could be used as a viable indicator of the progression of the disease and evaluation of cardiac function at an early stage.
The goal of cardiac motion estimation is to compute the optical flow representing the displacement vectors between consecutive 3D frames of a 4D cine CMR dataset, an image registration problem. To date, a number of approaches for motion estimation from cine MRI have been studied, including optical flow-based registration methods [2] and techniques based on feature tracking [3]. Metaxas et al. [4] proposed a physics-based framework for reconstructing the motion of the LV and RV from MRI-SPAMM (Spatial Modulation of Magnetization) data. Here, the authors deform the computed dynamic models with forces computed from the automatically segmented boundary data-points. Similarly, Park et al. [5] presented the use of finite element methods (FEM) to recover the right ventricle (RV) motion using parameter functions.
Recent approaches involve integrating anatomical data into a consistent framework to build patient-specific models. Hoogendoorn et al. [6] proposed a bilinear model for the extrapolation of cardiac motion assuming that the motion of the heart is independent of its shape. Xi et al. [7] proposed a bi-ventricular computational model to analyze ventricular mechanics in a pulmonary arterial hypertension patient from cine cardiac MRI images.
Although cardiac cine MRI has provided a non-invasive method for studying global and regional function of the heart, most of these studies have been centered on the LV. In light of the thin wall structure of the RV and its asymmetric geometry, there have only been very few research endeavors exploring the kinematics of RV, including the extraction of the RV motion and generation of patient-specific RV anatomical models. The goal of this work is to develop an approach for extracting the RV motion from cine cardiac MR image sequences and generate deformable endocardial RV models that can be later used to study RV kinematics as a biomarker for studying RV-related cardiac disease.
In this work, we propose a deep learning-based approach for extracting the frame-to-frame RV motion from cine cardiac images, and using this motion, along with segmented isosurface meshes at ED, to generate dynamic, deformable models of the RV. Here, we illustrate the potential of the CNN-based 4D deformable registration technique to build dynamic patient-specific RV models across subjects with normal and abnormal RVs. We used the segmented mask of the RV endocardium at all cardiac frames generated via our previously proposed CondenseUNet [8], which substitutes the concept of both standard convolution and group convolution (G-Conv) with learned group-convolution (LG-Conv). Following segmentation of the ED cardiac frame, we generate isosurface meshes, which we then propagate through the cardiac cycle using the CNN-based registration fields. Lastly, we compare these propagated isosurface meshes to those generated directly from the segmentation masks obtained from CondenseUNet [8].
II. Methodology
A. Imaging Data
For this study, we used the Automated Cardiac Diagnosis Challenge (ACDC) dataset1, consisting of short-axis cardiac cine-MR images acquired for 150 patients divided into 5 subgroups: normal (NOR), myocardial infarction (MINF), dilated cardiomyopathy (DCM), hypertrophic cardiomyopathy (HCM), and abnormal right ventricle (ARV), available through the 2017 MICCAI ACDC challenge [9]. The MRI images were acquired using two different MRI scanners of 1.5 T and 3.0 T magnetic strength. The series of short axis slices cover the LV from base to apex such that one image is captured every 5 mm to 10 mm with a spatial resolution of 1.37 mm2/pixel to 1.68 mm2/pixel. The image intensity values are normalized such that the pixel values lie in between 0 and 1.
B. Segmentation
The segmentation of the MR images is the first step towards extracting anatomical information for incorporation into geometric models. In this study, we used our previously proposed CondenseUNet [8] framework, which substitutes the concept of both standard convolution and group convolution (G-Conv) with learned group convolution (LG-Conv). Our network learns the group convolution automatically during training through a multi-stage scheme. The capability of our network to learn the group structure allows multiple groups to re-use the same features via condensed connectivity. Moreover, the efficient weight-pruning methods lead to high computational savings without compromising segmentation accuracy [10].
C. Slice Misalignment Correction
One of the main challenges with cardiac image acquisition is to account for cardiac motion due to respiration, which can lead to severe artifacts that manifest themselves by an overall misalignment of the 2D image slices. Numerous techniques for motion compensation have been proposed for preprocessing as well as post-processing the cardiac images. We leverage the slice misalignment correction method proposed by Dangi et al. [11] where we train a modified version of the U-Net model [12] to segment the cardiac chambers, namely the – LV blood-pool, LV myocardium and RV blood-pool, from 2D cardiac MRI images. We identify the LV blood-pool center, i.e., the centroid of the predicted segmentation mask, and stack the 2D cardiac MRI slices such that the LV blood-pool centers from each slice are collinear, hence correcting for any slice misalignment. This technique results in a set of correctly aligned image slice stack that faithfully represents the cardiac geometry and reduces the presence of stair-step artifacts that appear at the edges of the segmented features.
D. Deformable Registration Framework
Here we use a deep learning registration approach that employs the VoxelMorph [13] framework, as illustrated in Fig. 1. We focus on the deformable registration of 3D cardiac images after slice misalignment correction, as described in Section II-C. We follow the approach as described in [14], [15] and a convolutional neural network (CNN), G(f, m) with parameters θ is used to map the fixed and moving images to the parameters of the transformation.
Fig. 1.
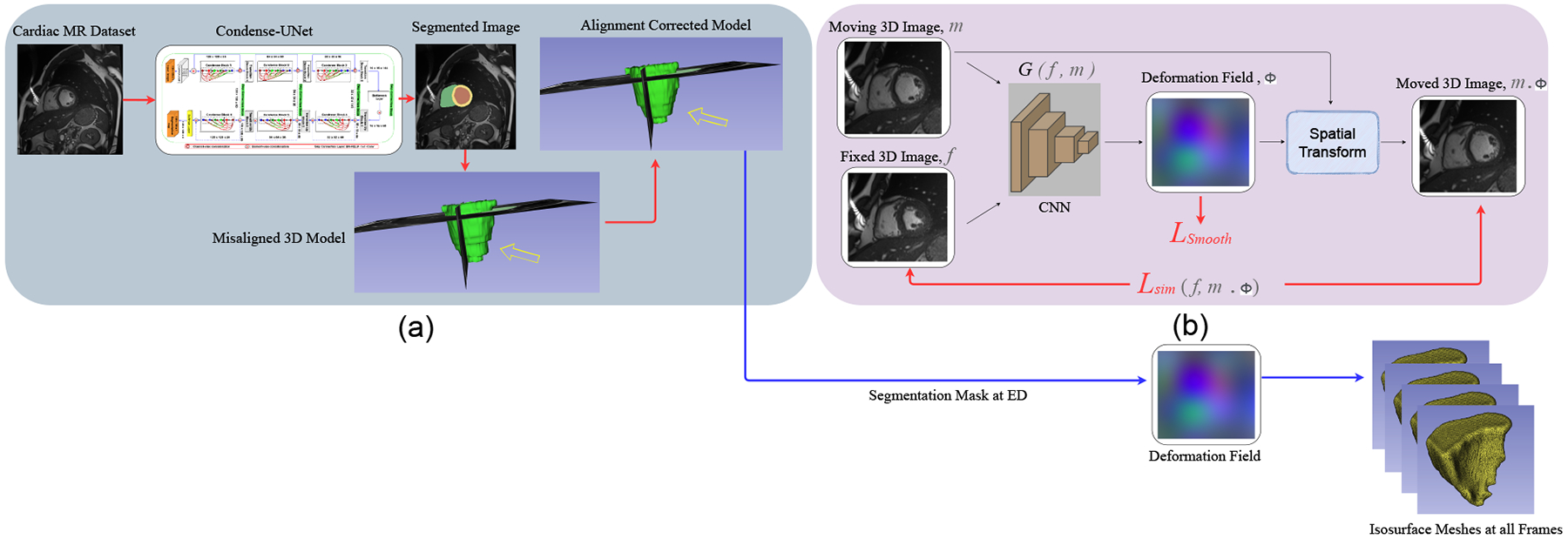
Image segmentation and deformable registration pipeline: a) ED frame segmentation and slice misalignment correction; b) deep learning registration framework. The CNN G(f, m) learns to predict the deformation field and register the moving 3D image to the fixed 3D image to generate the transformed image using the spatial transformation function.
During training, a sequence of cardiac 3D MR image pairs , where NT is the total number of frames, and mED is the end-diastole image frame, are passed to the CNN to generate the deformation field ϕ. The moving ED frame mED is then warped using the deformation field ϕ to obtain the transformed 3D image mED ◦ ϕ, which is then used to compute the similarity loss , with f being the fixed / target image. We iterate over pairs of fixed-moving images in a training dataset to find the network parameters that minimize the similarity loss , which is additionally constrained with a smoothing loss . Formally the overall objective function is written as:
| (1) |
where is the mean squared error (MSE), λ is the regularization parameter, and is a regularization on the deformation field ϕ to further enforce smoothness spatially as given by
| (2) |
where Δ is the Laplacian operator that takes into consideration both global as well as local properties of the objective function, as inspired by Zhu et al. [16]. We found that our model performs best with λ = 10 3.
E. Isosurface Mesh Extraction
The surface mesh generation pipeline contains two main tasks: surface mesh generation and smoothing. The predominant algorithm for isosurface extraction from original 3D data is marching cubes [17], which produces a triangulation within each cube to approximate the isosurface by using a look-up table of edge intersections. For this purpose, we used the segmentation map of all the frames in a cardiac cycle generated by our CondenseUNet model. Since the slice thickness was large and ranged from 5 mm to 10 mm, we re-sampled the dataset to achieve a 1 mm consistent slice thickness. After extracting the isosurface models using the Lewiner marching cubes [17] algorithm implemented using the scikit-image library [18] in the Python programming language, our next task was to remove the surface noise by applying smoothing operations. In order to smooth the isosurface meshes, we used the joint smoothing technique in 3D Slicer 4.10.2 [19], with the smoothing factor in the range of 0.15 to 0.2. This mesh smoothing operation significantly improves mesh appearance as well as shape, by moving mesh vertices without modifying topology.
Besides the RV isosurface meshes generated from the individual cardiac image frame segmentations following marching cubes and smoothing, which served as ground truth, we generated three additional sets of meshes by propagating the isosurface mesh at the ED phase to all the subsequent cardiac frames using the registration field estimated using the proposed VoxelMorph registration, as well as two traditional nonrigid image registration methods: the B-spline free form deformation (FFD) [20] algorithm and the fast symmetric force Demon’s algorithm [21], [22], as detailed in Section II-F.
F. Baseline Comparisons:
The results obtained using the proposed deep learning registration framework were compared to those obtained using traditional iterative image registration methods, including the FFD [20] algorithm and the fast symmetric force Demon’s algorithm [22]. The FFD registration method was implemented in SimpleElastix [23]. The FFD algorithm was set to use the adaptive stochastic gradient descent method as the optimizer, MSE as the similarity measure, binding energy as the regularization function, and was optimized in 500 iterations. The Demon’s algorithm was implemented in SimpleITK [24]. The standard deviations for the Gaussian smoothing of the total displacement field was set to 1 and optimized in 500 iterations. These algorithms are trained using manually tuned parameters on an Intel(R) Core(TM) i9-9900K CPU.
III. Results and Discussion
To evaluate the registration performance of the FFD, Demon’s and VoxelMorph methods, the isosurface of the right ventricle (RV) generated from the segmentation map in the ED frame is propagated to all the subsequent cardiac frames using the registration field. We then compare the registration accuracy by measuring the overlap between the isosurfaces directly generated by segmenting all cardiac image frames using our CondenseUNet model [8] (i.e., “silver standard”) and those propagated by FFD, Demon’s and VoxelMorph using Dice score and mean absolute distance (MAD).
Table I summarizes the registration performance between these propagated and “silver standard” isosurfaces, for both normal and abnormal RV. Fig. 2 illustrates the MAD between the propagated and segmented isosurfaces for one patient each with normal and abnormal RV. It can be observed that the CNN-propagated isosurfaces are closer to the segmented isosurfaces than the FFD-propagated isosurfaces; they are comparable to the Demon’s-propagated isosurfaces.
TABLE I.
RV Endocardium Mean (std-dev) Dice score (%) and mean absolute distance (MAD) between FFD and segmentation (FFD-SEG), Demon’s and segmentation (Dem-SEG), CNN and segmentation (CNN-SEG), ffd and CNN (FFD-CNN), and Demon’s and CNN (Dem-CNN) results. Statistically significant differences were confirmed via t-test between FFD-SEG and Dem-SEG, and FFD-SEG and CNN-SEG (* p < 0.1 and ** p < 0.05).
| Methods | Normal RV | Abnormal RV | ||
|---|---|---|---|---|
| Dice | MAD | Dice | MAD | |
| FFD-SEG | 75.47 (5.71) | 4.37 (1.23) | 81.72 (3.32) | 2.39 (0.62) |
| Dem-SEG | 79.49 (4.77)** | 3.52 (0.93) | 84.54 (4.75)** | 2.14 (0.46) |
| CNN-SEG | 79.51 (4.93)** | 3.34 (0.82)* | 83.61 (4.96)** | 2.44 (0.63) |
| FFD-CNN | 80.15 (5.86) | 1.69 (1.02) | 87.31 (3.45) | 1.03 (0.56) |
| Dem-CNN | 84.91 (5.58) | 1.08 (0.91) | 90.64 (2.55) | 0.78 (0.31) |
Fig. 2.
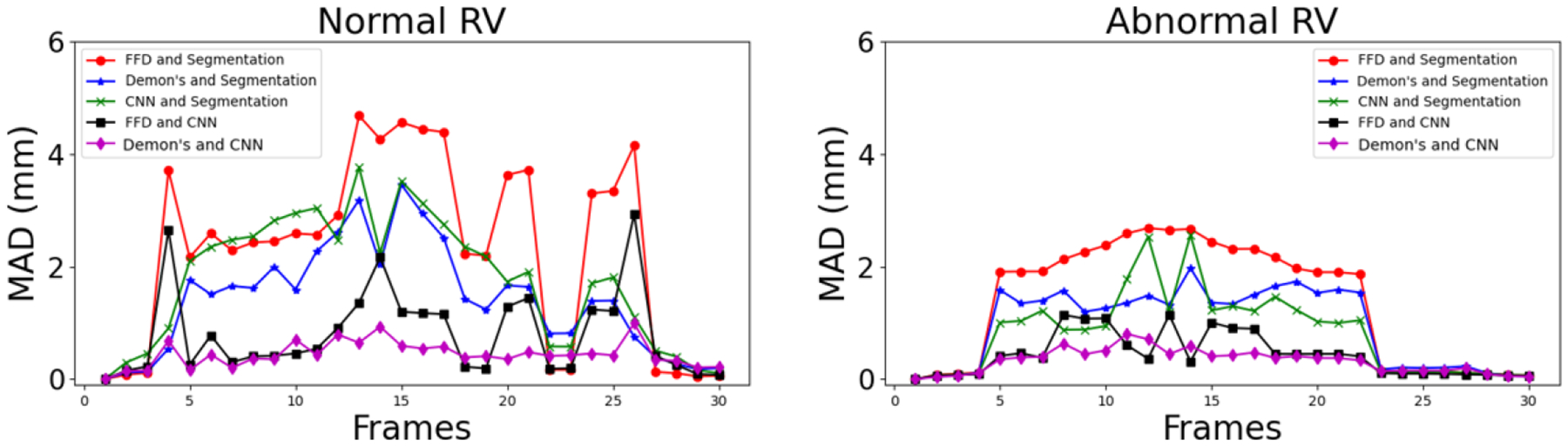
Mean absolute distance (MAD) between FFD-, Demon’s- and CNN-propagated and segmented (i.e., “silver standard”) masks at all cardiac frames for patients with normal and abnormal RVs.
As mentioned in Section II-E, we generate four sets of isosurface meshes at each frame of the cardiac cycle for one patient with a normal RV and one patient with an abnormal RV. Fig. 3 shows the mean nearest neighbor (NN) distance between the three sets of the registration-propagated isosurface meshes and the isosurface meshes generated directly from the segmented masks at each frame of the cardiac cycle for both the normal and abnormal RV subjects. It can be observed that the isosurface meshes are in close agreement with one another in the subjects with both a normal and an abnormal RV. Fig. 4 illustrates the model-to-model distance at the end-systole (ES) frame between the three registration-propagated isosurface meshes and the isosurface meshes generated directly from the segmented masks for both the normal and abnormal RV subjects.
Fig. 3.
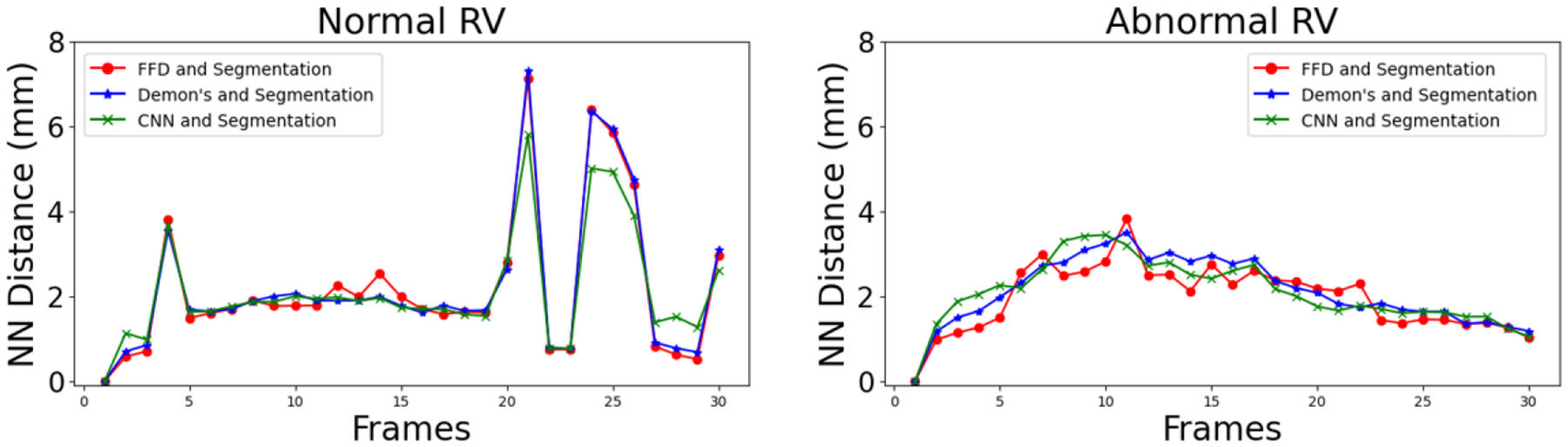
Nearest neighbor (NN) distance between FFD-, Demon’s- and CNN-propagated and segmented (i.e., “silver standard”) isosurface meshes at all cardiac frames for patients with normal and abnormal RVs.
Fig. 4.
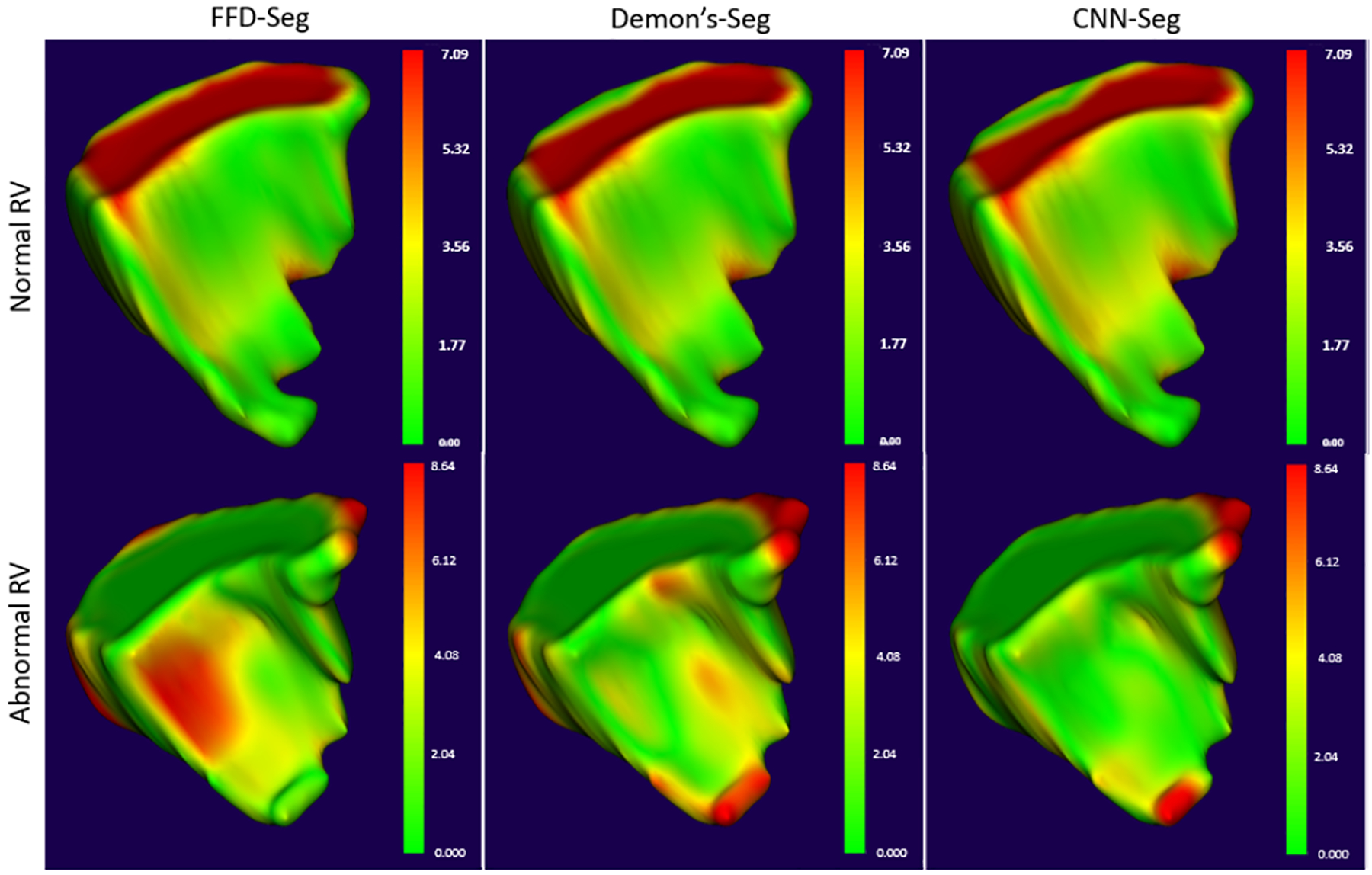
Model-to-model distance between the isosurface mesh at end-systole (ES) frame generated from segmentation and propagated using FFD, Demon’s and CNN-based deformable registration methods (left to right) for a patient with normal RV (top) and a patient with abnormal RV (bottom).
The proposed CNN-based cardiac motion extraction can be used to generate isosurface meshes at all the cardiac phases, which are in close agreement with the isosurface meshes propagated using traditional iterative image registration algorithms, as well as the meshes generated from the direct segmentation of the cardiac image frames.
One of the major advantages of the proposed CNN-based framework over the traditional nonrigid image registration techniques is the significantly faster computing time. For example, it takes around 40 seconds to propagate the isosurface mesh at the ED frame to the other frames of the cardiac cycle using a trained VoxelMorph model, compared to 135 and 160 seconds using the FFD and Demon’s registration methods, respectively. Similarly, the advantage of using mesh propagation rather than direct mesh generation from individual cardiac image frame segmentation is point correspondence across meshes at different frames, as well as an overall smoother mesh animation over sequential frames, since the individual frame segmentation is accompanied by inherent uncertainty. One area of improvement is to impose diffeomorphic restrictions to the CNN-based image registration method in order to prevent mesh tangling and maintain high mesh quality.
IV. Conclusion
This paper presents an unsupervised deep learning-based deformable image registration technique to generate individualized anatomically detailed RV models from high resolution cine cardiac MR images. The cardiac motion estimation was formulated as a 4D image registration problem, which constrains the smoothness of the estimated motion fields concurrently with the image registration procedure. The performance of this 4D registration method for cardiac applications has been evaluated by qualitative, as well as quantitative validation using cardiac cine MR images. In addition, our method is not restricted to only the RV geometry and can be extended to bi-ventricular models. Thus, it can be used potentially for improving early diagnosis and treatment planning of cardiomyopathies. As part of future work, we will use the deformable endocardial RV models to characterize the kinematics of the RV endocardium and study the displacement, velocity and acceleration, as well as shape changes and use these quantities as potential biomarkers across various RV-specific cardiac diseases, such as pulmonary hypertension or other cardiac conditions resulting from RV malfunction.
Acknowledgments
This work was supported by grants from the National Science Foundation (Award No. OAC 1808530, OAC 1808553 & CCF 1717894) and the National Institutes of Health (Award No. R35GM128877).
Footnotes
References
- [1].Benjamin et al. Heart disease and stroke statistics—2019 update: a report from the American Heart Association. Circulation, 139(10):e56–e528, 2019. [DOI] [PubMed] [Google Scholar]
- [2].Gao et al. Estimation of cardiac motion in cine-MRI sequences by correlation transform optical flow of monogenic features distance. Physics in Medicine & Biology, 61(24):8640, 2016. [DOI] [PubMed] [Google Scholar]
- [3].Moody et al. Comparison of magnetic resonance feature tracking for systolic and diastolic strain and strain rate calculation with spatial modulation of magnetization imaging analysis. Journal of Magnetic Resonance Imaging, 41(4):1000–1012, 2015. [DOI] [PubMed] [Google Scholar]
- [4].Metaxas et al. Automated segmentation and motion estimation of LV/RV motion from MRI. In Proceedings of the Second Joint 24th Annual Conference and the Annual Fall Meeting of the Biomedical Engineering Society][Engineering in Medicine and Biology, volume 2, pages 1099–1100. IEEE, 2002. [Google Scholar]
- [5].Park et al. A finite element model for functional analysis of 4D cardiac-tagged MR images. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 491–498. Springer, 2003. [Google Scholar]
- [6].Hoogendoorn et al. Bilinear models for spatio-temporal point distribution analysis. International Journal of Computer Vision, 85(3):237–252, 2009. [Google Scholar]
- [7].Xi et al. Patient-specific computational analysis of ventricular mechanics in pulmonary arterial hypertension. Journal of Biomechanical Engineering, 138(11), 2016. [DOI] [PubMed] [Google Scholar]
- [8].Kamrul Hasan SM and Linte Cristian A. CondenseUNet: A memory-efficient condensely-connected architecture for bi-ventricular blood pool and myocardium segmentation. In Medical Imaging 2020: Image-Guided Procedures, Robotic Interventions, and Modeling, volume 11315, page 113151J. International Society for Optics and Photonics, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Bernard et al. Deep learning techniques for automatic MRI cardiac multi-structures segmentation and diagnosis: Is the problem solved? IEEE Transactions on Medical Imaging, 37(11):2514–2525, 2018. [DOI] [PubMed] [Google Scholar]
- [10].Kamrul Hasan SM and Linte Cristian A. L-CO-Net: Learned condensation-optimization network for segmentation and clinical parameter estimation from cardiac cine MRI. In 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), pages 1217–1220. IEEE, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Dangi et al. Cine cardiac MRI slice misalignment correction towards full 3D left ventricle segmentation. In Medical Imaging 2018: Image-Guided Procedures, Robotic Interventions, and Modeling, volume 10576, page 1057607. International Society for Optics and Photonics, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Ronneberger et al. U-Net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 234–241. Springer, 2015. [Google Scholar]
- [13].Balakrishnan et al. VoxelMorph: A learning framework for deformable medical image registration. IEEE Transactions on Medical Imaging, 38(8):1788–1800, 2019. [DOI] [PubMed] [Google Scholar]
- [14].Upendra et al. A convolutional neural network-based deformable image registration method for cardiac motion estimation from cine cardiac MR images. In 2020 Computing in Cardiology, pages 1–4. IEEE, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Upendra et al. CNN-based cardiac motion extraction to generate deformable geometric left ventricle myocardial models from cine MRI. In International Conference on Functional Imaging and Modeling of the Heart, page TBD. Springer, 2021. arXiv preprint https://arxiv.org/abs/2103.16695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Zhu et al. New loss functions for medical image registration based on VoxelMorph. In Medical Imaging 2020: Image Processing, volume 11313, page 113132E. International Society for Optics and Photonics, 2020. [Google Scholar]
- [17].Lewiner et al. Efficient implementation of marching cubes’ cases with topological guarantees. Journal of Graphics Tools, 8(2):1–15, 2003. [Google Scholar]
- [18].van der Walt Stéfan et al. Scikit-image: Image processing in Python. PeerJ, 2:e453, 6 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Fedorov et al. 3D Slicer as an image computing platform for the quantitative imaging network. Magnetic Resonance Imaging, 30(9):1323–1341, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Rueckert et al. Nonrigid registration using free-form deformations: Application to breast MR images. IEEE Transactions on Medical Imaging, 18(8):712–721, 1999. [DOI] [PubMed] [Google Scholar]
- [21].Pennec Xavier, Cachier Pascal, and Ayache Nicholas. Understanding the “Demon’s algorithm”: 3D non-rigid registration by gradient descent. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 597–605. Springer, 1999. [Google Scholar]
- [22].Dru Florence and Vercauteren Tom. An ITK implementation of the symmetric log-domain diffeomorphic Demons algorithm. 2009.
- [23].Marstal et al. SimpleElastix: A user-friendly, multi-lingual library for medical image registration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pages 134–142, 2016. [Google Scholar]
- [24].Yaniv et al. SimpleITK image-analysis notebooks: A collaborative environment for education and reproducible research. Journal of Digital Imaging, 31(3):290–303, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]


