Abstract
Deep learning algorithms are emerging as powerful alternatives to compressed sensing methods, offering improved image quality and computational efficiency. Unfortunately, fully sampled training images may not be available or are difficult to acquire in several applications, including high-resolution and dynamic imaging. Previous studies in image reconstruction have utilized Stein’s Unbiased Risk Estimator (SURE) as a mean square error (MSE) estimate for the image denoising step in an unrolled network. Unfortunately, the end-to-end training of a network using SURE remains challenging since the projected SURE loss is a poor approximation to the MSE, especially in the heavily undersampled setting. We propose an ENsemble SURE (ENSURE) approach to train a deep network only from undersampled measurements. In particular, we show that training a network using an ensemble of images, each acquired with a different sampling pattern, can closely approximate the MSE. Our preliminary experimental results show that the proposed ENSURE approach gives comparable reconstruction quality to supervised learning and a recent unsupervised learning method.
Keywords: Unsupervised learning, SURE, parallel MRI
1. INTRODUCTION
MRI is a non-invasive imaging modality that gives excellent soft-tissue contrast. Several acceleration methods have been introduced to overcome the slow nature of MRI acquisition, thus improving patient comfort and reducing costs. Compressed sensing (CS) [1] can reconstruct MR images from fewer k-space samples using a computational algorithm. Recently, deep learning based techniques were introduced to minimize the computational complexity of the reconstruction algorithms by several orders of magnitude. Most of the current methods learn the parameters of the network from a large dataset of fully-sampled and noise-free images. Unfortunately, fully sampled and noise-free training data is not available or difficult to be acquired in several MR applications, such as high-resolution MRI.
The main focus of this work is on unsupervised deep learning, where fully-sampled noise-free images are not needed for training. The proposed unsupervised framework is broadly applicable to both model-based methods, which explicitly ensures the data-consistency during reconstruction [2–8], as well as direct-inversion methods [9, 10]. As compared to supervised, unsupervised training for image reconstruction is more challenging and less studied. The deep image prior (DIP) [11] uses a CNN that is trained only using the measured data from the specific subject, where the structure of the CNN serves as an implicit regularizer. However, DIP requires early stopping by manually observing the images, while resulting in a sub-optimal reconstruction quality compared to supervised learning methods. A recent work, in [12], proposes a CycleGAN based method for dynamic contrast enhancement in MR angiography. Self-supervised learning via data undersampling (SSDU) [13] suggests partitioning the measured k-space into two disjoint sets. The first set is used in the data consistency step, and another set is used for measuring the MSE loss.
The Stein’s unbiased risk estimate (SURE) [14] of mean-square-error (MSE) has been widely used to find regularization parameters in denoising problems [15] and recently to train deep denoisers [16]. The generalized SURE (GSURE) approach extended SURE to inverse problems, where an estimate of the projection of the MSE to the range of the measurement operator was considered [17]; this approach is also used to determine regularization parameters of inverse problems. A challenge in directly using GSURE to train deep image reconstruction algorithm in an end-to-end fashion is the poor approximation of the MSE by the projected MSE, especially in compressed sensing applications [16]. Hence, the LDAMP-SURE [16] algorithm relies on training different denoisers at each iteration in a message-passing iterative algorithm using the SURE loss [16, 18].
In this work, we propose an ensemble SURE (ENSURE) loss for the end-to-end training of image reconstruction algorithms. We first show that a weighted loss metric obtained from an ensemble of images, each acquired with a different sampling pattern, is an unbiased estimate for the MSE. We illustrate the proposed approach in the special cases of single-channel and multichannel MRI. The preliminary experiments demonstrate that proposed ENSURE approach can give comparable results to supervised training in both direct-inversion and model-based settings, while improving upon [13].
2. BACKGROUND
2.1. Inverse problems
We consider the case where an image ρ is only known through its measurements from the acquisition operator parameterized by the random vector s. The vector s can be viewed as the k-space sampling mask. The forward model representing the measurement process is given by
| (1) |
We assume the noise n to be Gaussian distributed with zero mean and covariance matrix C such that n ~ N(0, C). The probability density of ys is given by .
Deep learning methods have been introduced to reconstruct fully sampled image from noisy and undersampled measurements ys. The recovery using a deep neural network fΦ with trainable parameters Φ can be represented as
| (2) |
Here fΦ can be a direct-inversion or a model-based deep neural network. Most of the current deep learning solutions rely on supervised training, where fully sampled images are used as ground truth. However, it is challenging to acquire fully sampled data in many cases.
2.2. Unsupervised learning for denoising
The unsupervised learning of denoising algorithms (i.e, when ) have been extensively studied, resulting in popular schemes such as Noise2Noise [19] and Noise2Void [20]. Recently, several researchers have adapted the Stein’s unbiased risk estimate (SURE) [14] for the unsupervised training of deep image denoisers [16, 18]. When , SURE methods use an unbiased estimate of the mean-square error (MSE) as
| (3) |
This scheme has been demonstrated in [16,18] for the training of deep learned denoisers.
2.3. Unsupervised learning for inverse problems
SURE methods has been extended to inverse problems in [17] with rank deficient operators, where the original MSE is approximated by the projected MSE as
| (4) |
where is the projection operator to the range space of . This extension was considered for the training of deep learned inverse problems in [16]. However, in applications involving heavily undersampled measurements, MSEs is a poor approximation of MSE; current methods report poor results from end-to-end learning using SURE [16]. The LDAMP-SURE algorithm in [16] instead relies on layer-by-layer training of deep learning denoisers, assuming the noise at each iteration to be Gaussian distributed. This approach suffers from some deficiencies. First, this approach relies on approximate message passing algorithm and is not directly applicable to general model-based or direct inversion algorithms. Second, LDAMP-SURE was implemented for small images with Gaussian measurement matrices. Finally, we note that the end-to-end supervised training offers improved performance than layer-by-layer training strategies; we expect to obtain improved performance by end-to-end unsupervised training, provided improved loss functions were available. The proposed ENSURE approach is applicable to any direct-inversion and model-based unrolled networks. In this work, we evaluate our proposed approach on more general measurement matrices with complex-valued parallel MR images.
3. PROPOSED ENSEMBLE SURE (ENSURE)
To overcome the poor approximation of the MSE by MSEs, we consider the sampling of each image by a different operator. In the MRI context, we assume the k-space sampling mask s to be a random vector drawn from the distribution S. Note that this acquisition scheme is realistic and can be implemented in many applications. For instance, it may be difficult to acquire a specific image in a fully sampled fashion due to time constraints. However, one could use a different undersampling mask for each image , the image manifold.
Instead of the projected MSE in (4), we first consider the expectation of the projected MSE, computed over different sampling patterns and images. If is the sufficient statistic for the model in (1), we have
| (5) |
Using properties of expectation operator and projection matrices, (5) simplifies to weighted MSE term
| (6) |
The derivation is detailed in [21]. If the sampling distribution S is chosen appropriately, one can guarantee that W = is a full-rank matrix with high probability. In the single channel MRI setting, W corresponds to weighting the k-space data by the density of the samples. Depending on the probability distribution of the operators S, some subspace components may be weighted more than others. To compensate for this weighting, we now consider the weighted version of the projected MSE using the matrix W−1. We hence consider a weighted version of (6), denoted by
| (7) |
Specifically, we choose the operator Ws =W−1Ps depending on the sampling pattern. The expression in (7) allows estimating the true MSE from only the undersampled measurements. It is impossible to compute (7) since it depends on the ground truth images . We hence approximate it by its unbiased ENSURE estimate.
Lemma 1 Let denote a family of sampling operators measuring images ρ ∈ I, and let fϕ be a weakly differentiable reconstruction network. Then the loss in (7) is equal to
| (8) |
where
| (9) |
is the least-square solution of (1). represents the divergence of the network fΦ with respect to its input us.
Proof is shown in [21]. We now consider two special cases of single-channel and multi-channel MRI.
3.1. Single-channel MRI
In the single-channel setting , where is the Fourier transform and S is the sampling matrix. Here, . We assume the probability of a specific k-space sample to be acquired as a Bernoulli distribution with a probability ωi, which may be varying spatially; a variable density distribution with higher density in the center of k-space is a common choice in compressed sensing application. The expectation of the projection operators Ps in this case yields . In this case, the data term in (8) simplifies to
| (10) |
We evaluate the divergence term using Monte-Carlo SURE approach [22].
3.2. Multichannel MRI
In the context of parallel MRI, the sampling operator is given by , where C denotes the coil sensitivity weighting, denotes the Fourier transform and S denotes the multichannel sampling matrix. Here, we rely on computed using the conjugate gradient based SENSE algorithm, which solves
| (11) |
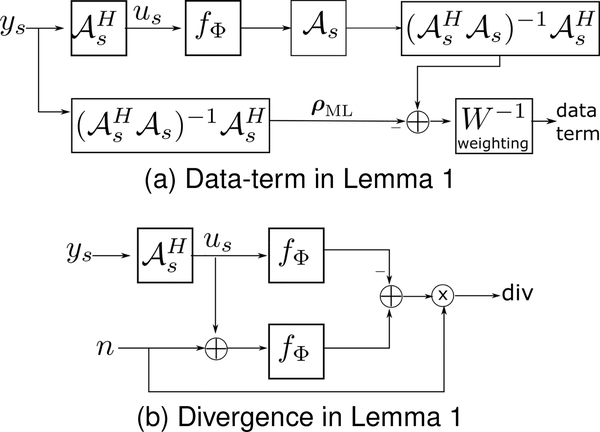
with λ → 0. The projection Psρ of ρ onto the range space of is obtained by solving (11). In this work, we choose for simplicity, which will undo the low-pass weighting of the MSE introduced by the averaging in (4). The outline of the data term and the divergence term are shown in Fig. 1.
Fig. 1.
Visual representation of the computation of the data and divergence terms in the proposed ENSURE estimate in (8). Here, ⨁ and ⊗ represent the addition and inner-product, respectively.
We note that for each sampling pattern, the data term involves the difference between the reconstructed image and the corresponding CG-SENSE solution. However, we only compare the projection of the errors onto the range space of the measurement operator, evaluated using CG-SENSE of the measurements of the errors. An additional weighting is used to compensate for the non-uniform density of the sampling patterns in k-space. The divergence term may be viewed as a network regularization, which serves to minimize noise amplification. We compute the divergence term using Monte-Carlo approximation [22]. Note that the use of the data term alone will result in overfitting, similar to observations in deep image prior methods as the number of epochs increase. As shown by the theory, the averaging of the sum of the error measures and divergence terms over a variety of sampling patterns closely approximate the MSE, without requiring ground truth images [21].
4. EXPERIMENTS AND RESULTS
We consider a parallel MRI brain data obtained using a 3-D T2 CUBE sequence with Cartesian readouts using a 12-channel head coil at the University of Iowa on a 3T GE MR750w scanner. The matrix dimensions were 256 × 232 × 208 with a 1 mm isotropic resolution. Fully sampled multichannel brain images of nine volunteers were collected, out of which data from five subjects were used for training, while the data from two subjects were used for testing and the remaining two for validation.
We compare the proposed ENSURE approach with a supervised learning approach named MoDL [3] and a recent unsupervised learning approach named SSDU [13]. We also compare the performance in direct-inversion and model-based frameworks. The direct inversion approach had a standard 18-layer ResNet architecture with 3×3 filters and 64 feature maps at each layer. Both SSDU and MoDL had the same architecture with 5-repetitions of ResNet and data consistency with shared weights. For SSDU, we used 60% of measured k-space for data consistency step and 40% for MSE estimation, as suggested in the [13]. The real and imaginary components of complex data were used as channels in all the experiments.
Table 1 shows results of proposed ENSURE approach on the test dataset at six-fold acceleration and noise of standard deviation σ = 0.01. It also shows comparison of SSDU [13] with the proposed ENSURE approach. The proposed approach results in higher peak signal to noise ratio (PSNR) and structural similarity index (SSIM) as compared to SSDU.
Table 1.
Comparison of PSNR and SSIM values in the direct-inversiona and model-based framework at six-fold acceleration in the presence of Gaussian noise of std=0.01.
| Framework | Direct-Inversion | Model-Based | ||
|---|---|---|---|---|
| Algorithm | PSNR | SSIM | PSNR | SSIM |
| SSDU [13] | 31.85 | 0.79 | 37.89 | 0.94 |
| ENSURE | 32.67 | 0.88 | 38.44 | 0.96 |
| Supervised | 34.85 | 0.95 | 39.31 | 0.98 |
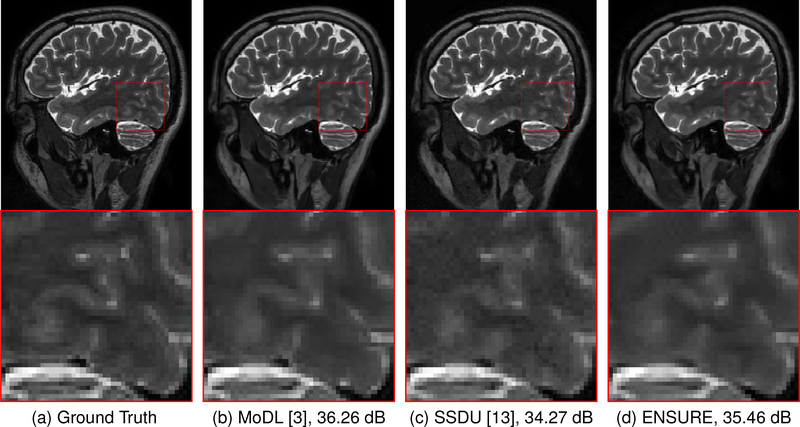
Figure 2 compares the visual quality obtained from the proposed unsupervised learning using the ENSURE approach with a supervised learning and an existing unsupervised learning (SSDU) approach at six-fold acceleration and noise std=0.03. It is clear from the zoomed region that the proposed ENSURE approach provides cleaner reconstruction than the existing SSDU approach.
Fig. 2.
Reconstruction results at 6x acceleration and noise std=0.03 in the model-based framework. The proposed ENSURE estimate of the MSE can reach the performance of supervised training (in (b)) where MSE is used as loss function.
5. CONCLUSIONS
We proposed an unsupervised learning approach for linear inverse problems with non-trivial measurement operator. We showed that projected MSE is equivalent to weighted MSE when expected over an ensemble of sampling operators. We further derive an unbiased estimate, ENSURE, for the inverse weighted MSE. Here, we omitted the proof of Lemma 1 due to space constraints. The current experiments are limited to a relatively small dataset as a proof of concept.
Acknowledgments
This work is supported by 1R01EB019961-01A1. This work was conducted on an MRI instrument funded by 1S10OD025025-01
6. REFERENCES
- [1].Candes Emmanuel and Romberg Justin, “Sparsity and incoherence in compressive sampling,” Inverse problems, vol. 23, no. 3, pp. 969, 2007. [Google Scholar]
- [2].Hammernik Kerstin, Klatzer Teresa, Kobler Erich, Recht Michael P., Sodickson Daniel K., Pock Thomas, and Knoll Florian, “Learning a Variational Network for Reconstruction of Accelerated MRI Data,” Magnetic resonance in Medicine, vol. 79, no. 6, pp. 3055–3071, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Aggarwal Hemant K, Mani Merry P, and Jacob Mathews, “MoDL: Model based deep learning architecture for inverse problems,” IEEE Trans. Med. Imag, vol. 38, no. 2, pp. 394–405, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Pramanik Aniket, Aggarwal Hemant, and Jacob Mathews, “Deep generalization of structured low-rank algorithms (Deep-SLR),” IEEE Transactions on Medical Imaging, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Adler Jonas and Öktem Ozan, “Learned primal-dual reconstruction,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1322–1332, 2018. [DOI] [PubMed] [Google Scholar]
- [6].yang yan, Sun Jian, Li Huibin, and Xu Zongben, “Deep ADMM-Net for compressive sensing MRI,” in Advances in Neural Information Processing Systems 29, 2016, pp. 10–18. [Google Scholar]
- [7].Yang Guang, Yu Simiao, Dong Hao, Slabaugh Greg, Dragotti Pier Luigi, Ye Xujiong, Liu Fangde, Arridge Simon, Keegan Jennifer, Guo Yike, et al. , “DAGAN: Deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1310–1321, 2017. [DOI] [PubMed] [Google Scholar]
- [8].Schlemper Jo, Caballero Jose, Hajnal Joseph V, Price Anthony N, and Rueckert Daniel, “A deep cascade of convolutional neural networks for dynamic MR image reconstruction,” IEEE Trans. Med. Imag, vol. 37, no. 2, pp. 491–503, 2018. [DOI] [PubMed] [Google Scholar]
- [9].Han Yoseob, Sunwoo Leonard, and Ye Jong Chul, “k-space deep learning for accelerated MRI,” IEEE Trans. Med. Imag, 2019. [DOI] [PubMed] [Google Scholar]
- [10].Ronneberger Olaf, Fischer Philipp, and Brox Thomas, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI). Springer, 2015, pp. 234–241. [Google Scholar]
- [11].Ulyanov Dmitry, Vedaldi Andrea, and Lempit-sky Victor, “Deep image prior,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 9446–9454. [Google Scholar]
- [12].Cha Eunju, Chung Hyungjin, Kim Eung Yeop, and Ye Jong Chul, “Unpaired training of deep learning tmra for flexible spatio-temporal resolution,” IEEE Transactions on Medical Imaging, 2020. [DOI] [PubMed] [Google Scholar]
- [13].Yaman Burhaneddin, Hosseini Seyed Amir Hossein, Moeller Steen, Ellermann Jutta, Kâmil Uğurbil, and Akçakaya Mehmet, “Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data,” Magnetic resonance in medicine, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Stein Charles M, “Estimation of the mean of a multivariate normal distribution,” The annals of Statistics, pp. 1135–1151, 1981. [Google Scholar]
- [15].Blu Thierry and Luisier Florian, “The sure-let approach to image denoising,” IEEE Transactions on Image Processing, vol. 16, no. 11, pp. 2778–2786, 2007. [DOI] [PubMed] [Google Scholar]
- [16].Metzler Christopher A, Mousavi Ali, Heckel Reinhard, and Baraniuk Richard G, “Unsupervised learning with stein’s unbiased risk estimator,” arXiv preprint arXiv:1805.10531, 2018. [Google Scholar]
- [17].Eldar Yonina C, “Generalized sure for exponential families: Applications to regularization,” IEEE Transactions on Signal Processing, vol. 57, no. 2, pp. 471–481, 2008. [Google Scholar]
- [18].Zhussip Magauiya, Soltanayev Shakarim, and Chun Se Young, “Training deep learning based image denoisers from undersampled measurements without ground truth and without image prior,” in IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 10255–10264. [Google Scholar]
- [19].Lehtinen Jaakko, Munkberg Jacob, Hasselgren Jon, Laine Samuli, Karras Tero, Aittala Miika, and Aila Timo, “Noise2noise: Learning image restoration without clean data,” in International Conference on Machine Learning, 2018, pp. 2965–2974. [Google Scholar]
- [20].Krull Alexander, Buchholz Tim-Oliver, and Jug Florian, “Noise2void-learning denoising from single noisy images,” in IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 2129–2137. [Google Scholar]
- [21].Aggarwal Hemant Kumar, Pramanik Aniket, and Jacob Mathews, “ENSURE: Ensemble Stein’s Unbiased Risk Estimator for Unsupervised Learning,” in arXiv, 2021, https://arxiv.org/abs/2010.10631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Ramani Sathish, Blu Thierry, and Unser Michael, “Monte-carlo sure: A black-box optimization of regularization parameters for general denoising algorithms,” IEEE Transactions on image processing, vol. 17, no. 9, pp. 1540–1554, 2008. [DOI] [PubMed] [Google Scholar]