Abstract
We introduce a novel image regularization termed as multiple degree total variation (MDTV). This type of regularization combines the first and second degree directional derivatives, thus providing a good balance between preservation of edges and region smoothness. In order to solve the resulting optimization problem, we proposed a fast majorize minimize algorithm. We demonstrate the utility of the MDTV regularization in the context of image denoising and compressed sensing. We compare the proposed method with standard TV, and the state of the art higher degree methods, including higher degree total variation (HDTV) and total generalized variation (TGV) based schemes. Numerical results indicate that MDTV penalty provides improved image recovery performance.
I. Introduction
Image recovery from their noisy partial measurements has been a significant research topic in a wide range of imaging applications including medical imaging, remote sensing, and microscopy. The common approach is to formulate the image recovery problem as an optimization problem which is the combination of data consistency and regularization term. Total variation (TV) is one of the most commonly used regularization penalty in many inverse problems [1]. The main reason for the good performance of TV regularization is due to its capability to preserve sharp edges in the image. However, the main limitation of TV penalty is that it generates patchy or staitcasing artifacts in the reconstructed images since TV promotes gradient sparsity. To overcome the problem associated with TV penalty, researchers have proposed different modifications of TV promoting higher order derivatives sparsity. Among them there are regularizations using derivatives of a single higher order degree. For example, the Laplacian penalty [2], [3], the anisotropic second order regularization [4], [5], the Hessian Schatten-norm regularizations [6]. However, the L1 norm of the Laplacian has a high-dimensional null space [7], which tends to preserve pointlike features rather than sharp edges. The anisotropic second order penalty is not rotation invariant, which makes it not ideal for the regularization of the image recovery problem. Moreover, it has been proved that many of the second degree TV penalties are special cases or equal to the HDTV regularization [8]. Another family of functionals involve image derivatves of different degrees, including the infimal-convolution functional which combines TV with higher order derivatives [9], and total generalized variation (TGV) [10].
We recently proposed a family of convex functionals named higher degree TV (HDTV), which are defined as the L1-Lp norm (p ≥ 1) of the nth degree directional derivatives [8], [11]. HDTV penalties possess the desirable properties of TV, such as rotation invariance, preservation of edges. Moreover, HDTV scheme overcomes the problems associated with TV, while enhances the line like features of an image. Numerical experiments have demonstrated that HDTV penalties provide desirable image reconstruction results and improve the image quality significantly compared with TV. However, since HDTV focuses on derivatives of a single degree, it still has some limitations in accurately recovering an image.
In this work, we propose a family of image regularizations which combine the first and second degree directional derivative to improve the performance of HDTV penalties. The novel type of image regularizations are termed as multiple degree TV (MDTV), which are defined as the L1-Lp (p ≥ 1) norm of all rotations of the weighted norm of the 1st and 2nd degree derivative operator. The MDTV penalties have the similar properties as TV and HDTV, such as rotation invariance, translation invariance, convexity, and scale covariance. Furthermore, by balancing the weights of the first and second degree directional derivatives, MDTV selectively regularizes the image based on various features, which lead to a more natural recovery of the images. In order to solve the resulting optimization problem, we propose an iteratively reweighted majorize minimize algorithm similar as in [11], which successively approximates the optimal solution by minimizing a sequence of quadratic surrogate functions. We demonstrate the utility of MDTV in the context of image denoising and compressed sensing. Numerical results show that the proposed method yields improved image quality over standard TV penalty, the state of the art HDTV regularization, and the TGV scheme.
II. Background
A. Regularized inverse problems for image recovery
We consider the recovery of a continuously differential complex image from its noisy measurments b. Here, Ω is the spatial support of the complex image f. The measurements b is modeled as: , where n is the Gaussian distributed white noise and is a linear operator representing the image acquisition process. Under most practical scenarios, the operator is ill-conditioned. In such cased, in order to make the problem well-posed, the image recovery problem is generally formulated as a constrained optimization problem:
| (1) |
where represents data fidelity, is the regularization term, and we choose the parameter α to obtain the optimal solution, i.e., the maximized signal to noise ratio.
B. Generalized higher degree total variation
We have shown in [11] that by reinterpreting the standard two-dimensional total variation (TV) regularization as a mixed norm of image directional derivatives, we could obtain higher degree total variation (HDTV) regularizations, defined as
| (2) |
where fθ,n(r) is the nth degree directional derivative of f along the direction uθ = (cos(θ), sin(θ)), defined as
| (3) |
The HDTV penalty (2) is termed as isotropic and anisotropic HDTV, when p = 2 and p = 1, respectively.
According to the property of rotation steerability of the directional derivative, fθ,n(r) can be expressed as
| (4) |
where sn(θ) is the vector of trigonometric polynomials, and gn(r) is the vector of nth degree partial derivatives.
III. Multiple degree total variation (MDTV) regularized image restoration
A. MDTV regularization
We use the combination of the first and second order derivative to obtain a new type of regularization penalty, termed as MDTV penalty, which is defined as
| (5) |
where fθ,1(r), fθ,2(r) are the first and second order directional derivative separately, and λ1, λ2 are the weighting coefficients for balancing the first and second order directional derivatives. For simplicity purpose, we define λ1 + λ2 = 1.
Note that the MDTV penalty is the L1-L1 norm of the directional derivatives similar as the anisotropic type of HDTV penalties proposed in [11]. However, instead of using a single higher degree derivative, MDTV uses the combined weighted L2 norm of the first and second degree directional derivatives. By tuning λ1 and λ2, the optimal performance of MDTV penalty can be achieved for image recovery. The tuning of the balancing parameters will be discussed in the later section. According to the definition of MDTV (5), TV and HDTV penalties are two special cases of the MDTV regularization. When λ1 = 1, λ2 = 0, MDTV becomes standard TV penalty. Similarly, when λ1 = 0, λ2 = 1, MDTV becomes the HDTV penalty.
Therefore, the MDTV regularized image recovery scheme is specified by
| (6) |
B. Numerical algorithm
We apply the fast majorize minimze algorithm to solve the optimization problem [11]. In the first step, the original optimization function is majorized as:
| (7) |
where and represent the first and second degree derivative majorization terms separately. Specifically,
| (8) |
| (9) |
where ω(m)(r, θ) is the weighting matrix, which is computed at each iteration using the values of (n = 1, 2) at the current mth iteration.
| (10) |
The small constant ϵ is included to ensure that the weighting matrix is finite in smooth image regions where the directional derivatives tend to be zeros. Using the steerability of the directional derivatives (4), in (8) and (9) can be rewritten as
| (11) |
Here, the spatially varying weighting matrix could be defined as
| (12) |
The first and second degree derivative majorization terms (11) thus become
| (13) |
Substituting (13) and (7) in (6), and ignoring the constant terms, we could solve for the following majorization cost function iteratively to obtain the optimal image recovery results:
| (14) |
We propose to use conjugate gradient algorithm to solve (14), with the corresponding gradient expressed as
| (15) |
C. Discretization of the derivative operator
The above introduced MDTV penalties are defined for continuous images. In practical implementations, The derivatives are approximated using finite difference. For example, the derivative of the 2D signal along the x dimension is approximated as q[k, l] = f[k+1, l]−f[k, l] = Δ1 ∗ f, which can be viewed as the convolution of f by , where ψ(x) = ∂β1(x)/∂x and β1(x) is the first degree B-spline function [12]. In order to further obtain discrete operators that are approximately rotation steerable, we approximate the nth degree partial derivatives as follows:
| (16) |
for all , where denotes the nth order derivative of the dth (d = n1 + n2) degree B-spline and δ is chosen based on the following rule:
| (17) |
The shift δ is chosen so that the image derivatives are evaluated at the intersection of the pixels instead of the midpoint of the pixels. Since B-spline functions approximate Gaussian functions as the degree increases, the tensor product of B-spline functions are approximately rotation steerable.
D. Choice of the parameters
MDTV regularized optimization problem requires optimized regularization parameters to ensure ideal image recovery results. In addition, MDTV needs a proper balancing between the first and second order directional derivatives. For each noise level and operator, we determine the optimal parameters to obtain the optimized signal to noise ratio (SNR), which is computed as
| (18) |
where is the reconstructed image, forig is the original image, and ∥ · ∥F is the Frobenius norm.
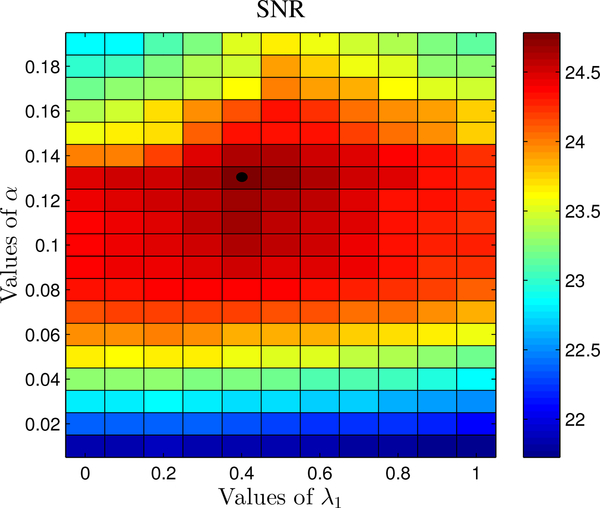
In order to check how the SNR values of the recovered images behave as a function of the regularization parameter α and the weighting parameters λ1 and λ2, we plot the parameters optimization results in Fig. 1. Specifically, we tuned for the parameters for the denoising of the Lena image with additive Gaussian noise with standard deviation σ = 0.04. We choose α = 0.01, 0.02, 0.03, …, 0.19 and λ1 = 0, 0.1, 0.2, …, 1. Note that λ2 = 1, 0.9, …, 1 correspondingly. The plot indicates that the SNR has a global maximum for different values of the parameters. We also observe that the optimal parameters are mostly dependent on each setting, but not much on the specific image.
Fig. 1.
SNR values of the denoised Lena image as function of the parameters α and λ1. The original image was contaminated with Gaussian white noise with standard deviation σ = 0.04. The dotted region corresponds to the maximum SNR value, where the optimal parameters were chosen, i.e.,λ1 = 0.4, α = 0.13. Note that the first and the last column corresponds to HDTV denoising and TV denoising, respectively.
IV. Results
The performance of the proposed MDTV regularized method is investigated in the context of image denoising and compressed sensing. We use the signal to noise ratio (SNR) to assess the quality of the recovered images.
A. Denoising
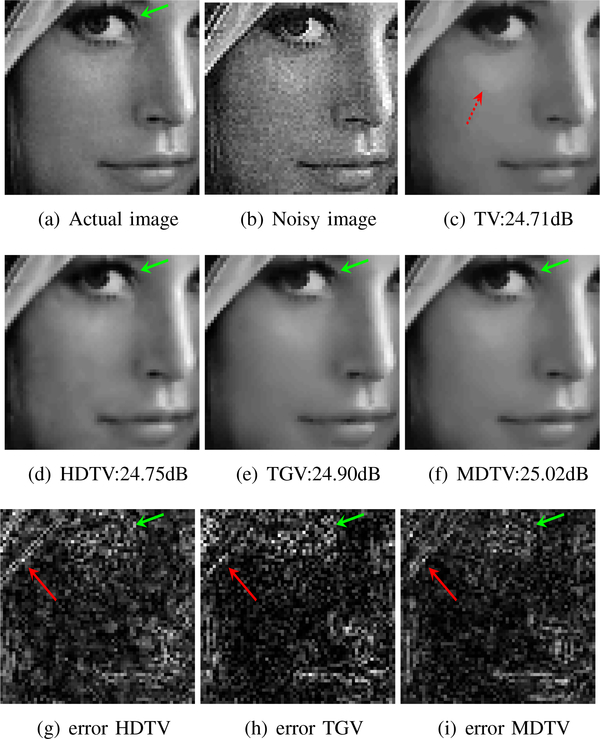
We compare the denoising performance of MDTV method with standard TV, HDTV, and TGV regularized schemes using the Lena image in Fig. 2. The image is corrupted with additive Gaussian whilte noise of standard deviation of σ = 0.04. We show the zoomed image for better visual comparison. The results show that TV leads to patchy recovered image, indicated in red dotted arrow. The HDTV method overcomes the patchy artifacts and preserves more details. Compared with HDTV, TGV scheme provides smoother and more natural recovered image. The proposed MDTV method preserves most of the details, indicated in green arrow. The red arrows in the error images show that MDTV scheme is capable of preserving the linelike features, compared with the other methods.
Fig. 2.
Denoising results of the Lena image. (a) and (b) show the actual image and the noisy version containing Gaussian white noise of standard deviation σ = 0.04. (c)-(f): Denoised images using TV, HDTV, TGV, and MDTV methods, respectively. (g)-(i): Error images of the denoised results using HDTV, TGV, and MDTV schemes.
The denoising results on four 256 × 256 images using TV, HDTV, TGV, and the proposed MDTV methods with different noise levels are reported in Table I. The standard deviation of the noise is chosen to be 0.02–0.06. We observe from the results that the proposed methods consistently outperforms the other methods with an improvement of the SNR around 0.5dB.
TABLE I.
Comparison of denoising algorithms
| Lena | Peppers | |||||
| σ | 0.02 | 0.04 | 0.06 | 0.02 | 0.04 | 0.06 |
| TV | 29.02 | 24.71 | 22.28 | 31.42 | 27.18 | 24.89 |
| HDTV | 29.10 | 24.75 | 22.39 | 31.85 | 27.42 | 25.27 |
| TGV | 29.22 | 24.90 | 22.59 | 31.91 | 27.61 | 25.21 |
| MDTV | 29.31 | 25.02 | 22.58 | 32.05 | 27.73 | 25.40 |
| Cameraman | Microscopy | |||||
| σ | 0.02 | 0.04 | 0.06 | 0.02 | 0.04 | 0.06 |
| TV | 31.58 | 26.60 | 24.27 | 33.26 | 28.10 | 26.78 |
| HDTV | 31.73 | 26.72 | 24.46 | 33.49 | 28.38 | 26.95 |
| TGV | 31.80 | 26.68 | 24.56 | 33.65 | 28.42 | 26.12 |
| MDTV | 31.98 | 27.05 | 24.70 | 33.75 | 28.61 | 26.29 |
B. Compressed sensing
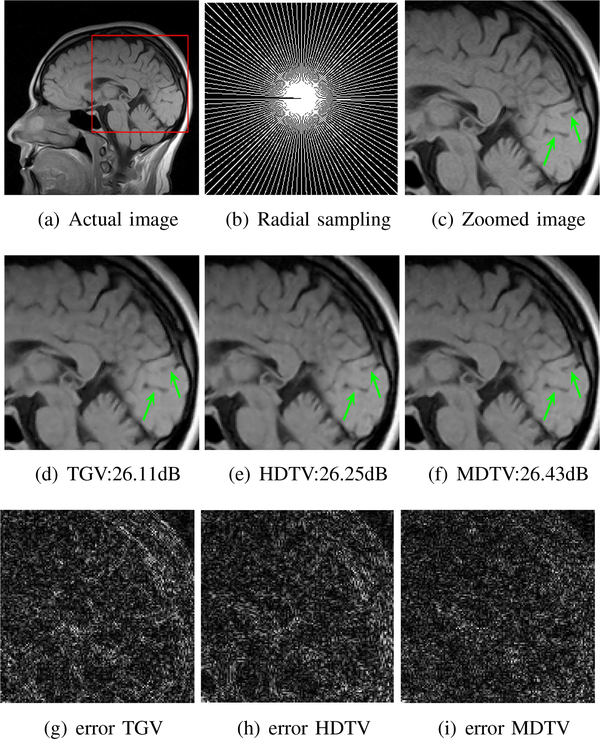
In this section, we consider the reconstruction of MR images from incomplete compressed sensing measurements. We use four MR images, including brain, wrist, angiography, and ankle MR image to validate the proposed method. In the experiments, we assume that the measurements are acquired using radial undersampling pattern. Fig. 3 shows the reconstructions of the brain MR image using HDTV, TGV, and the proposed MDTV methods from 60 radial sampling lines. We observe that the proposed method is capable of recovering the details and the linelike features most accurately compared with HDTV and TGV schemes, indicated by the green arrows.
Fig. 3.
Recovery of the brain MR image from the undersampled measurements. (a)-(c): The actual image, the radial undersampling pattern, and the zoomed version of the original image. (d)-(f): Reconstructions using HDTV, TGV, and the proposed MDTV method. (g)-(i): Error images.
The SNRs of the reconstructed images using TV, HDTV, TGV, and MDTV methods with different number of radial lines are showed in Table II. One can see that the propose MDTV methods consistently provides results with highest SNR among all of the algorithms.
TABLE II.
Comparison of compressed sensing algorithms
| Brain | Angiography | |||||
| Lines | 40 | 60 | 100 | 40 | 60 | 100 |
| TV | 22.38 | 25.93 | 30.96 | 19.35 | 23.31 | 28.60 |
| HDTV | 22.66 | 26.25 | 31.30 | 19.61 | 23.46 | 28.87 |
| TGV | 22.53 | 26.11 | 31.23 | 19.50 | 23.32 | 28.81 |
| MDTV | 22.76 | 26.33 | 31.35 | 19.73 | 23.68 | 28.95 |
| Wrist | Ankle | |||||
| Lines | 40 | 60 | 100 | 40 | 60 | 100 |
| TV | 20.35 | 23.70 | 28.89 | 17.55 | 20.03 | 24.30 |
| HDTV | 20.65 | 23.86 | 29.12 | 17.59 | 20.01 | 24.35 |
| TGV | 20.59 | 23.73 | 29.03 | 17.80 | 20.15 | 24.51 |
| MDTV | 20.75 | 24.07 | 29.25 | 17.74 | 20.32 | 24.64 |
V. Conclusion
We proposed a MDTV regularization penalty for image recovery, which is the L1-L1 norm of the balanced combination of the first and the second degree directional derivatives. We used an efficient majorize minimize algorithm to solve the resulting optimization problem. Numerical comparisons of the proposed method with the standard TV, HDTV, and TGV regularization schemes show that MDTV regularized method leads to an improved image recovery performance.
Acknowledgments
This work is supported by NSF awards CCF-0844812 and CCF-1116067.
Contributor Information
Yue Hu, School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin, China.
Mathews Jacob, Department of Electrical and Computer Engineering, University of Iowa, IA, USA.
References
- [1].Rudin LI, Osher S, and Fatemi E, “Nonlinear total variation based noise removal algorithms,” Physica D: Nonlinear Phenomena, vol. 60, no. 1, pp. 259–268, 1992. [Google Scholar]
- [2].Chan T, Marquina A, and Mulet P, “High-order total variation-based image restoration,” SIAM Journal on Scientific Computing, vol. 22, no. 2, pp. 503–516, 2000. [Google Scholar]
- [3].You Y-L and Kaveh M, “Fourth-order partial differential equations for noise removal,” Image Processing, IEEE Transactions on, vol. 9, no. 10, pp. 1723–1730, 2000. [DOI] [PubMed] [Google Scholar]
- [4].Lysaker M, Lundervold A, and Tai X-C, “Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time,” Image Processing, IEEE Transactions on, vol. 12, no. 12, pp. 1579–1590, 2003. [DOI] [PubMed] [Google Scholar]
- [5].Esedoglu S and Osher SJ, “Decomposition of images by the anisotropic rudin-osher-fatemi model,” Communications on pure and applied mathematics, vol. 57, no. 12, pp. 1609–1626, 2004. [Google Scholar]
- [6].Lefkimmiatis S, Ward JP, and Unser M, “Hessian schatten-norm regularization for linear inverse problems,” Image Processing, IEEE Transactions on, vol. 22, no. 5, pp. 1873–1888, 2013. [DOI] [PubMed] [Google Scholar]
- [7].Kybic J, Blu T, and Unser M, “Generalized sampling: A variational approach,” in Proc. 2001 Intl Conf. Sampl. Theory and Appl, 2001, pp. 151–154. [Google Scholar]
- [8].Hu Y, Ongie G, Ramani S, and Jacob M, “Generalized higher degree total variation (HDTV) regularization,” Image Processing, IEEE Transactions on, vol. 23, no. 6, pp. 2423–2435, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Chambolle A and Lions P-L, “Image recovery via total variation minimization and related problems,” Numerische Mathematik, vol. 76, no. 2, pp. 167–188, 1997. [Google Scholar]
- [10].Bredies K, Kunisch K, and Pock T, “Total generalized variation,” SIAM Journal on Imaging Sciences, vol. 3, no. 3, pp. 492–526, 2010. [Google Scholar]
- [11].Hu Y and Jacob M, “Higher degree total variation (HDTV) regularization for image recovery,” Image Processing, IEEE Transactions on, vol. 21, no. 5, pp. 2559–2571, 2012. [DOI] [PubMed] [Google Scholar]
- [12].Unser M and Blu T, “Wavelet theory demystified,” Signal Processing, IEEE Transactions on, vol. 51, no. 2, pp. 470–483, 2003. [Google Scholar]