Abstract
We introduce a novel compartmental low rank algorithm for high resolution MR spectroscopic imaging. We model the field inhomogeneity compensated MRSI dataset as the sum of a lipid dataset and a metabolite dataset using the spatial compartmental information obtained from water reference data. Both these datasets are modeled as low-rank subspaces, and are assumed to be orthogonal to each other. We formulate the recovery of the dataset from spiral measurements as a low-rank recovery problem. Experiments using numerical phantom and in-vivo data demonstrates the ability of the algorithm to provide improved spatial resolution and nuisance signal free spectra.
Keywords: Magnetic resonance spectroscopic imaging, low rank modeling, nuisance removal, constrained reconstruction
1. INTRODUCTION
Magnetic resonance spectroscopic imaging (MRSI) is a popular imaging tool used to estimate the spatial distribution of various brain metabolites, which are of immense significance in characterizing neurological, psychiatric and metabolic diseases [1]. Unfortunately, the clinical potential of MRSI is thwarted by low signal to noise ratio(SNR) of metabolites, long scan times due to encoding in both chemical shift and spatial dimensions, as well as low resolution. Another challenge is the spectral leakage from the large unwanted nuisance signal from the subcutaneous lipid layer. Since the lipid signals are several orders of magnitude higher than the metabolites of interest, they often heavily corrupt the metabolite signals.
Several acquisition schemes were introduced to overcome the above challenges. For example, time-varying gradients have been introduced to improve spatial resolution and coverage in a specified scan time. Since these methods trade signal to noise ratio to extend the k-space coverage, the improvement in spatial resolution is hence fundamentally limited by the available SNR. Several methods to suppress lipids such as outer volume suppression, inversion recovery, inner volume excitation, and acquisition with longer echo times do exist. However, these methods often do not provide perfect suppression of lipids and are associated with partial loss of brain coverage or reduced SNR. Advanced image reconstruction schemes that rely on spatial priors [2, 3, 4, 5], sparsity priors[6], and spectral priors have been used to overcome the limited k-space coverage of MRSI. The central idea is to use high resolution spatial information from water reference data and spectral priors to constrain the reconstructions. A key problem with pre-determined priors is the risk of biasing the reconstruction, as well as loss in performance when the assumptions are violated. Recently, low-rank models [7, 8, 9] which learn the spatial/spectral basis functions from the measured MRSI data have been introduced to overcome this limitation. These powerful class of methods have the potential to significantly improve the recovery of MRSI data. A challenge in using global low-rank models is the high dynamic range of the MRSI signal; the lipid and residual water signal will dominate the basis functions, thus potentially attenuating the metabolite signals.
We introduce a compartmentalized low-rank algorithm for reconstruction of high resolution MRSI data with removal of residual nuisance signals. We model the field inhomogeneity compensated dataset as the sum of low-rank lipid and metabolite compartments. Inspired by [10], we exploit the orthogonality between metabolites and lipid basis functions to minimize lipid leakage artifacts. This enables us to recover the subspaces without imposing any prior knowledge about the spectral support of the metabolites or lipid signals. The low-rank penalty on the metabolites enables us to recover the higher resolution metabolite maps with minimal noise amplification. The proposed method has conceptual similarities to recent two-step low-rank based MRSI reconstruction scheme [11, 12], which rely on specialized processing steps on low-resolution MRSI data to extract the metabolite and lipid signals using their assumed spectral support; these basis functions are then used to recover the dataset from undersampled acquisitions. By contrast, the proposed approach automatically estimates the lipid and metabolite subspace from the measured data. Hence our approach is robust to line broadening of metabolites and lipids; the explicit use of the spectral location of the metabolite and fat peaks may be violated in practical applications with large field variations near the skull.
We compare the performance of the proposed scheme against the method described in [13] which penalizes compartmentalized smoothness to reduce noise, inhomogeneity distortions, and spectral leakage. Experimental data is collected using a spiral sequence with a matrix size 60 × 60 as described in [14] with 8 outer volume suppression bands for lipid suppression. Phantom simulations are also performed. The experiments show that the proposed method with low-rank regularization of metabolites produces superior quality maps with high resolution details while achieving denoising and nuisance removal. By contrast, the spatial details are smoothed out with the classical smoothness penalty regularization.
2. THEORY
We propose to estimate the spatial support of the brain (denoted by M) and the extra cranial lipid regions (denoted by L) from the water reference data. We model the spatio-temporal MRSI signal as the linear combination of metabolite and lipid signals:
| (1) |
where r is the spatial dimension and t is the temporal dimension. Here, XM is signal restricted to the spatial regions corresponding to the brain, and XL is the lipid compartment restricted to the support of the lipid region. We assume that the residual water signal is removed using pre-processing methods like HSVD [15]. We observe that the dynamic range of the signals in the respective compartments L and M are small, while the combined signal often has a very high dynamic range. The modeling of the entire dataset X(r, t) as a single low-rank subspace as in [8] may be counter-productive due to the huge dynamic range between the lipid and metabolite signals; the subspace will be dominated by lipid basis functions.
We denote the Casorati matrix corresponding to the signals XM and XL by XM and XL, respectively. Since the dynamic range of the signals within each spatial compartment is small and are contributed by finite number of distinct anatomic regions, we propose to model XM and XL as low-rank matrices. Even with the spatial separation, the high dynamic range between the signals will result in cross talk between XM and XL. We observe that the spectral signatures of metabolites and lipids are highly dissimilar. To minimize the cross-talk, we propose to exploit the orthogonality between the temporal/spectral profiles of XM and XL (rows of XM and XL, respectively).
We formulate the recovery as the optimization problem:
| (2) |
Here, is the forward model accounting for the non-uniform Fourier transform, field inhomogeneity distortion, and coil sensitivity encoding. b is the measured k-space data after water removal. In this work p is assumed to be 1.
2.1. Algorithm
We propose to use the iterative least square algorithm [16], originally introduced for nuclear norm minimization, to solve (2). This results in an iterative algorithm that alternates between the weighted least square problem:
| (3) |
and updating the weights
| (4) |
Here and . Here, Γε(Σ) is a stabilizing operator to prevent the singular values from becoming too small; every jth singular value of Σ = diag(σ1, σ2, …) is boosted by ε>0 if they become too small, as
| (5) |
Note that (3) has an intuitive justification. If the singular vectors of XM and XL decay rapidly, QM and QL can be viewed as the projection operators to the subspaces of XM and XL with insignificant singular values, respectively. Similarly, QO is a projection operator to the signal subspace of XL. Hence, solving (3) can be viewed as denoising the data by penalizing the null space projections of XL and XM, respectively. The last term constrains the signal spaces of lipids and metabolites to be orthogonal to each other. This prevents the huge lipid signals from dominating the metabolite signal subspace.
3. EXPERIMENTAL METHODS
We compare the proposed scheme of compartmentalized low rank with orthogonality, motivated by [10] against compartmentalized smoothness penalty as described in [13]. Compartmentalized smoothness prior also reduces cross-talk between different spatial regions.
We also process the data using the conventional pipeline, consisting of an inverse Fourier transform & field inhomogeneity compensation to demonstrate the benefit in using orthogonality priors and denoising. We evaluate the performance of the low-rank method and smoothness promoting method on simulated data and experimental data.
3.1. Numerical phantom
A digital brain phantom containing different compartments for CSF, white matter and gray matter is constructed on a 512 × 512 grid size. Each compartment is assigned a spectra containing NAA, Creatine, and Choline, based on known chemical shift locations. The intensities of the metabolites in CSF, white matter and gray matter are chosen as reported in literature for normal subjects. Lipid peaks, using standard six peak model, are added to an additional lipid layer to simulate residual lipid after suppression methods are used. All the basis sets are also broadened spectrally to simulate decay, using Gaussian damping. A B0 inhomogeneity map is simulated using fourth order polynomial in both the spatial dimensions.
We compute the Fourier samples of the phantom on the spiral trajectory as described in [14] at a matrix size of 60×60. Random Gaussian white noise is added to simulate measurement noise resulting in metabolite SNR of 18 dB.
3.2. Experimental data
Data is acquired with the same spiral trajectory as the numerical phantom, with matrix size 60 × 60 with 256 temporal frames [14]. A healthy volunteer was scanned at a Siemens 3T scanner with a 12 channel receiver headcoil. Eight fat saturation bands were used to suppress extra cranial lipids. The first repetition of the sequence is used to acquire water reference data. An axial slice of FOV= 240 mm2 was collected at TR/TE = 1500/55 ms and the scan time was 7.2 mins to collect 12 averages. The water data was processed to obtain high resolution field inhomogeneity maps and lipid and brain masks that characterize the spatial compartments as described in [17].
4. RESULTS
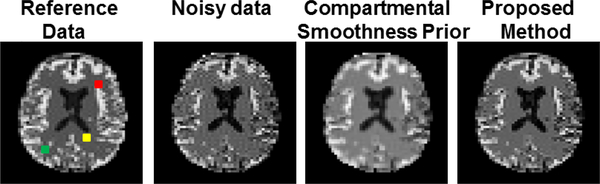
The results with the numerical phantom reconstructed at a grid size of 60×60 are shown in Fig. 1 and Fig. 2. The reference data is reconstructed using inverse Fourier transform of the spiral data before adding any noise or lipids or inhomogeneity distortion. The noisy data is reconsructed using the conventional pipeline of inverse Fourier transform and field inhomogeneity compensation. We observe that the algorithm with smoothness priors results in blurred edges. By contrast, the low rank prior preserves most of the fine details. This is due to the high frequency information being suppressed along with noise. Low rank prior performs with minimal loss of high frequency edge information. The spectra are denoised in both the methods but the compartmental smoothness prior still has some residual lipid peaks though it is reduced by penalizing cross talk between compartments.
Fig. 1.
NAA Maps of the simulated phantom are shown for the two methods. The noisy data is obtained by using the conventional pipeline of inverse Fourier transform & field inhomogeneity compensation. The RMSE of the maps for the noisy data, compartmental smoothness prior method and the proposed method are 5.08%, 7.2% and 2.8% respectively.
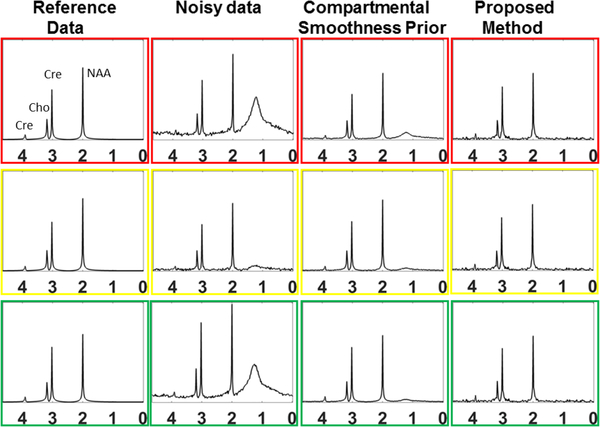
Fig. 2.
Spectra at 3 different pixels marked in the Fig 1 are shown for both the methods. The horizontal axis is in ppm. The noisy data obtained by the conventional pipeline shows lipid leakage and added noise.
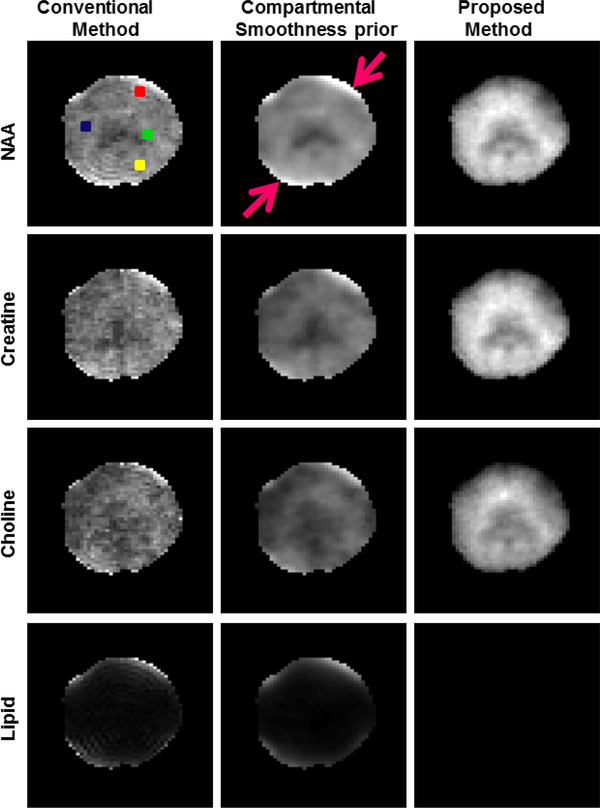
The results for the experimental data reconstructed at a grid size of 60 × 60 are shown in Fig. 3 and Fig. 4. The regularization parameters for both the regularized recovery methods were manually tuned to achieve denoising with as little smoothing of the maps as possible. The peak integral maps of NAA, Creatine, Choline, and Lipid are shown in Fig. 3 for both the methods. The data processed using the conventional pipeline (inverse Fourier transform & field inhomogeneity compensation) is shown in the first column for comparisons. We observe that this data is noisy and some of the pixels near the skull have considerable residual lipid leakage. The smoothness prior method also suffers form lipid leakage as expected, as marked by the arrows in the Fig. 3. The proposed method achieves better denoising and generates considerably improved spatial maps with spatial details, while the smoothness penalty is observed to oversmooth the data. The lipid maps show minimal lipid leakage artifacts for the proposed method. The spectra at four representative voxels marked in the reference image is shown in Fig. 4. The voxels close to the skull show lipid leakage in the conventional inverse Fourier transform reconstruction and the smoothness prior method.
Fig. 3.
Metabolite and lipid maps for the different methods are shown. The conventional method appears to be noisy whereas spatial details are lost with smoothness prior. Both these methods have lipid leakage in regions close to skull as pointed out by the arrows. The proposed method however gives superior quality maps without lipid artifacts.
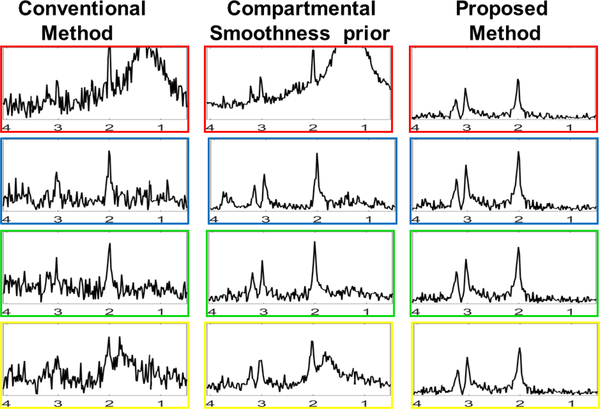
Fig. 4.
Spectra at 4 different pixels marked in the NAA map in Fig. 3 are shown.The horizontal axis is in ppm. Smoothness prior achieves denoising but the pixels close to the skull have lipid leakage.The spectra obtained from the proposed method are denoised and lipid leakage is removed.
5. CONCLUSION
In this paper we proposed a novel reconstruction scheme for low-rank recovery of MRSI data. We introduced a technique to learn the metabolite subspaces efficiently without imposing any prior spectral knowledge. We further demonstrated the improvement of low rank modeling of metabolite data over more popular smoothness constraint. High resolution maps are achieved while achieving denoising. This would be immensely beneficial for SNR deficient low resolution metabolic imaging.
Acknowledgments
This work is supported by grants ACS RSG-11-267-01-CCE, NSF CCF-1116067, and ONR-N000141310202.
6. REFERENCES
- [1].Posse S, Otazo R, Dager SR, and Alger J, “MR spectroscopic imaging: principles and recent advances.” J. Magn. Reson. Imaging, vol. 37, no. 6, pp. 1301–25, 2013. [DOI] [PubMed] [Google Scholar]
- [2].Hu X, Levin DN, Lauterbur PC, and Spraggins T, “SLIM: Spectral localization by imaging,” Magn Reson Med, vol. 8, no. 3, pp. 314–322, 1988. [DOI] [PubMed] [Google Scholar]
- [3].Liang Z-P and Lauterbur PC, “A generalized series approach to MR spectroscopic imaging,” IEEE Trans Med Imaging, vol. 10, no. 2, pp. 132–137, 1991. [DOI] [PubMed] [Google Scholar]
- [4].Jacob M, Zhu X, Ebel A, Schuff N, and Liang Z-P, “Improved model-based magnetic resonance spectroscopic imaging,” IEEE Trans Med Imaging, vol. 26, no. 10, pp. 1305–1318, 2007. [DOI] [PubMed] [Google Scholar]
- [5].Eslami R and Jacob M, “Robust reconstruction of MRSI data using a sparse spectral model and high resolution MRI priors.” IEEE Trans Med Imaging, vol. 29, no. 6, pp. 1297–309, 2010. [DOI] [PubMed] [Google Scholar]
- [6].Chatnuntawech I, Gagoski B, Bilgic B, Cauley SF, Setsompop K, and Adalsteinsson E, “Accelerated (1) H MRSI using randomly undersampled spiral-based k-space trajectories.” Magn Reson Med, vol. 74, no. July 2014, pp. 13–24, Jul. 2014. [DOI] [PubMed] [Google Scholar]
- [7].Liang Z-P, “Spatiotemporal imagingwith partially separable functio ns,” in Biomedical Imaging: From Nano to Macro, 2007. ISBI 2007. 4th IEEE International Symposium on IEEE, 2007, pp. 988–991. [Google Scholar]
- [8].Kasten J, Lazeyras F, and Van De Ville D, “Data-driven MRSI spectral localization via low-rank component analysis.” IEEE Trans. Med. Imaging, vol. 32, no. 10, pp. 1853–63, Oct. 2013. [DOI] [PubMed] [Google Scholar]
- [9].Nguyen HM, Peng X, Do MN, and Liang Z-P, “Denoising MR spectroscopic imaging data with low-rank approximations.” IEEE Trans. Biomed. Eng, vol. 60, no. 1, pp. 78–89, Jan. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Bilgic B, Gagoski B, Kok T, and Adalsteinsson E, “Lipid suppression in CSI with spatial priors and highly undersampled peripheral k-space.” Magn Reson Med, vol. 69, no. 6, pp. 1501–11, Jun. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Lam F and Liang Z-P, “A subspace approach to high-resolution spectroscopic imaging.” Magn Reson Med, vol. 71, no. 4, pp. 1349–57, Apr. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Ma C, Lam F, Johnson CL, and Liang Z-P, “Removal of nuisance signals from limited and sparse (1) H MRSI data using a union-of-subspaces model.” Magn Reson Med, vol. 00, pp. 1–10, Mar. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Eslami R and Jacob M, “A sparse reconstruction algorithm for parallel spiral MR spectroscopic imaging,” in Biomedical Imaging: From Nano to Macro, 2011 IEEE International Symposium on IEEE, 2011, pp. 93–96. [Google Scholar]
- [14].Bhave S, Eslami R, and Jacob M, “Sparse spectral deconvolution algorithm for noncartesian MR spectroscopic imaging.” Magn Reson Med, vol. 71, no. 2, pp. 469–76, 2014. [DOI] [PubMed] [Google Scholar]
- [15].Barkhuijsen H, De Beer R, and Van Ormondt D, “Improved algorithm for noniterative time-domain model fitting to exponentially damped magnetic resonance signals,” J Magn Reson, vol. 73, no. 3, pp. 553–557, 1987. [Google Scholar]
- [16].Fornasier M, Rauhut H, and Ward R, “Low-rank matrix recovery via iteratively reweighted least squares minimization,” SIAM J Optimization, vol. 21, no. 4, pp. 1614–1640, 2011. [Google Scholar]
- [17].Cui C, Wu X, Newell JD, and Jacob M, “Fat water decomposition using globally optimal surface estimation (GOOSE) algorithm.” Magn Reson Med, vol. 73, no. 3, pp. 1289–1299, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]