Abstract
We propose a model-based deep learning architecture for the correction of phase errors in multishot diffusion-weighted echo-planar MRI images. This work is a generalization of MUSSELS, which is a structured low-rank algorithm. We show that an iterative reweighted least-squares implementation of MUSSELS resembles the model-based deep learning (MoDL) framework. We propose to replace the self-learned linear filter bank in MUSSELS with a convolutional neural network, whose parameters are learned from exemplary data. The proposed algorithm reduces the computational complexity of MUSSELS by several orders of magnitude, while providing comparable image quality.
Keywords: K-space Deep learning, Echo Planar Imaging, Convolutional Neural Network
1. INTRODUCTION
Diffusion-weighted imaging (DWI) is widely used in neuroscience applications to study the microstructural and connectivity changes in the brain. The long readouts in singleshot echo planar imaging scheme (ssEPI), which is the main workhorse for DWI, often causes geometric distortions and blurring artifacts in the presence of magnetic field inhomogeneity. Several researchers have hence introduced multi-shot EPI (msEPI) methods, where the k-space acquisition is segmented into multiple shots. However, a challenge with msEPI-based DWI acquisition scheme is the phase inconsistency between the shots. Specifically, subtle physiological motion (e.g. cardiac pulsation) during the diffusion encoding gradients will result in the phase inconsistencies between the k-space data of the shots. If uncorrected, these phase errors translate to ghosting artifacts. Approaches to correct for these phase errors include navigator based methods to measure and correct for the phase errors, as well as methods such as MUSE [1] that estimate the phase errors.
We have recently introduced a multi-shot sensitivity-encoded diffusion data recovery algorithm using structured low-rank matrix completion (MUSSELS) [2]. This scheme enables the navigator-free joint recovery of the k-space data from all the shots. While this scheme can offer state of the art results, the challenge is the high computational complexity. Despite the existence of fast structured low-rank algorithms, the reconstruction of the high-resolution data from different directions and slices is challenging due to the large data size and the need for matrix lifting.
To minimize the computational complexity, we introduce a novel deep learning framework. The proposed scheme is motivated by our recent work on model-based deep learning (MoDL) [3] and related algorithms [4]. The main benefit of MoDL is the significantly reduced run time during image recovery/testing. The use of the conjugate-gradient algorithm within the network to enforce data consistency in MoDL provides improved performance for a specified number of iterations. The sharing of network parameters across iterations enables MoDL to keep the number of learned parameters decoupled from the number of iterations, thus providing good convergence without increasing the number of trainable parameters; the low number of trainable parameters translate to significantly reduced training data in data constrained medical imaging applications.
We first bring MUSSELS to the MoDL setting by using an iterative reweighted least-squares algorithm (IRLS); this algorithm alternates between a data-consistency block and a residual convolutional denoising block. The learning of the denoising filter coefficients from the data using low-rank minimization in MUSSELS is associated with high computational complexity. To realize a computationally efficient solution, we propose to replace the linear convolutional denoiser with a convolutional neural network (CNN); the CNN parameters are learned in an end-to-end fashion from exemplary data. While the implementation is similar to MoDL, the main difference is the extension to multichannel settings and the learning in the Fourier domain (k-space) motivated by the MUSSELS IRLS formulation. Specifically, the k-space formulation allows us to exploit the convolutional annihilation properties resulting from the phase relations between shots.
The proposed framework has similarities to recent k-space deep learning strategy [5], which also exploits convolutional relations in the Fourier domain. However, this approach relies on a direct approach that jointly learns the inverse of the forward model and the phase relations; it requires a considerably larger network with significantly more parameters, which translates to higher training data demand. The use of the forward model within our algorithm allows us to work with the significantly smaller network, which translates to reduced training data demand. In addition, the use of the conjugate gradients based data consistency blocks facilitates the direct recovery of parallel MRI data, which is vital in the multishot setting.
2. DEEP LEARNED MUSSELS
Let ρ and represent an N shot diffusion weighted image and its Fourier transform respectively. Then the image acquisition model in the presence of Gaussian noise n can be represented as:
| (1) |
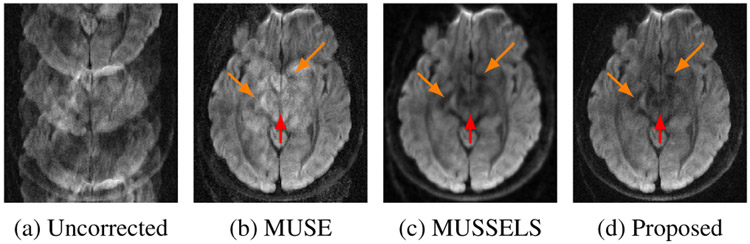
where . Here, , , and denotes the Fourier transform, sampling operation, and weighting with coil sensitivities, respectively. Note that the sampling indices of the different shots are complementary; the combination of the data from the different shots will result in a fully sampled image in the absence of phase errors. Unfortunately, the shots are often corrupted by phase errors, resulting from physiological motion during the diffusion encoding process. If uncorrected, the combination will exhibit severe ghosting artifacts as seen from Fig. 2(a).
Fig. 2.
Reconstructions using various methods corresponding to a given diffusion direction from the testing slice.
2.1. Brief Review of MUSSELS
MUSSELS capitalizes on the phase relations between the shots, as well as multichannel measurements, to fill in the missing data. The multiplicative phase relations translate to convolutional annihilation relations in Fourier domain (k-space), which are exploited by posing the joint recovery as a structured low-rank recovery scheme. Let ρ(r) represents the complex DW image where r represents the spatial location. The images corresponding to two different shots denoted by ρi(r) and ρj(r) differ by phase terms ϕi(r) and ϕj(r), respectively:
The key observation is that the above images satisfy an image domain annihilation relation [6]:
which can be represented in frequency domain as:
The above annihilation relation can also be expressed using the block-Hankel matrix representation as
where the matrix product correspond to 2-D convolution between and . These relations imply that the structured matrix , where is the matrix of multishot images, is low-rank. MUSSELS recovers the multi-shot images from their undersampled k-space measurements by solving:
| (2) |
where ‖ · ‖* denotes the nuclear norm. The above problem can be solved using iterative shrinkage algorithm [2].
2.2. IRLS reformulation of MUSSELS
To bring the MUSSELS framework to the MoDL setting, we first introduce an iterative reweighted least squares (IRLS) reformulation. The IRLS algorithm alternates between the enforcement of data consistency and a denoiser, which projects the k-space data to a constraint set. We note that the unrolled structure resembles MoDL, with the exception than the filters are estimated using low-rank matrix completion.
Using an auxiliary variable Z, we rewrite (2) as
| (3) |
We observe that (3) is equivalent to (2) as β → ∞. An alternating minimization algorithm to solve the above problem yields the following steps:
| (4) |
| (5) |
We now borrow from [7], where we majorize the nuclear norm term as where the weight matrix is specified by
| (6) |
Here, I is the identity matrix. Using the commutativity of convolution, T (Z) Q = G (Q) Z, where G (Q) is a structured block Hankel matrix formed from the columns of Q . The majorization of (5) yields
| (7) |
Differentiating the above expression and setting it equal to zero, we get . Using matrix inversion lemma and assuming λ << β, we approximate this step as
| (8) |
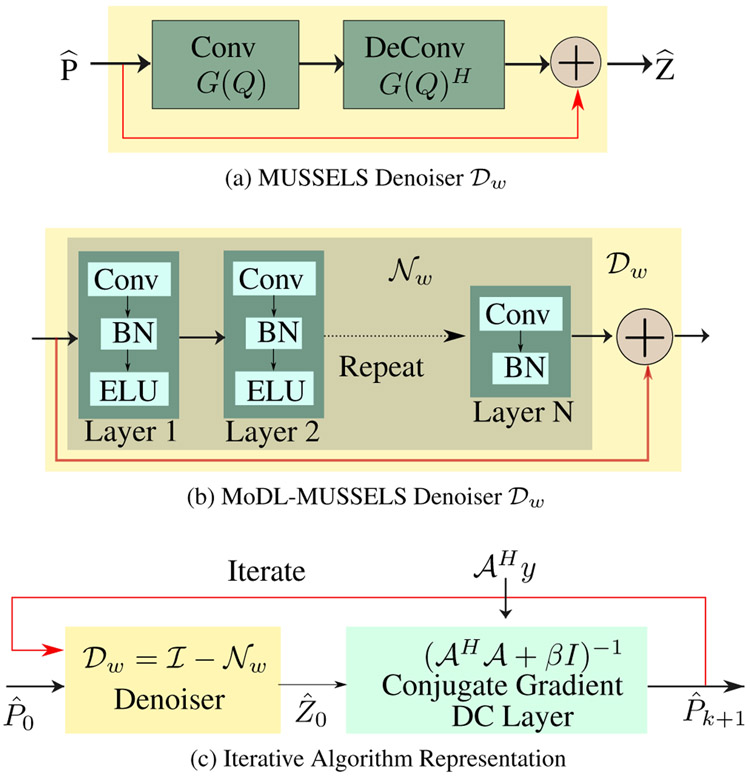
We note that (8) can be thought of as a residual block, which involves the convolution of the multishot signals with the columns of Q, followed by flipped convolutions (deconvolutions in deep learning context), and subtraction from as shown in Fig. 1a. One can think of Q as a surrogate the null-space of . Thus, the update (8) can be thought of as removing the components of in the null-space, which can be viewed as a denoising step.
Fig. 1.
(a). The representation of Eq. (8) as a convolutiondeconvolution network. (b) The Learnable denoiser. (c) The iterative algorithm where denoiser can be (a) for MUSSELS or (b) for MoDL-MUSSELS.
2.3. MoDL-MUSSELS
The MUSSELS scheme described above provides state of the art results [2]. However, the computational complexity of the structured low-rank algorithm is high, especially in the context of diffusion-weighted imaging where several directions need to be estimated for each slice. To minimize the computational complexity, we introduce a deep learning scheme where the denoising block specified by (8) is replaced by a residual learning based CNN block; see Fig. 1(b). The filter parameters of this non-linear block are learned from exemplary data. Our hypothesis is that the non-linear structure will facilitate the projection of the data orthogonal to the null space for an unseen dataset. The network alternates between the two steps
| (9) |
| (10) |
The data consistency step, specified by (9) is imposed as optimization block within the network as shown in Fig. 1c, implemented using conjugate gradient optimization scheme. Note from Fig. 1 that the structure of both algorithms is the same. The main difference from MUSSELS is that the self-learned Q filters are replaced by pre-learned residual deep convolutional block, denoted by . This framework is essentially a multi-channel extension of our model based deep learning scheme (MoDL); the main difference is that learning is performed in the Fourier domain instead of the image domain.
We use a N layer deep CNN with each layer having a convolution operation (conv) followed by batch normalization (BN) and a non-linear mapping. We use an exponential linear unit (ELU) non-linearity, specified by defined as
Note that the ReLU block attenuates the negative part of the input; the use of this non-linearity resulted in dc off-sets in k-space, which translates to a bright spot in the origin in the image. We empirically observe that the ELU block was less vulnerable to those errors. The input to the network is , which is the initial estimate of the reconstructed images obtained by solving the SENSE reconstruction.
3. EXPERIMENTS AND RESULTS
In-vivo diffusion data from a healthy volunteer (3T MRI scanner, 32-channel head coil) was used in the study. A dual spin-echo diffusion imaging sequence was used with a 4-shot EPI readout. A b-value of 1000 s/mm2 was used and measurements using 60 diffusion gradient were performed with NEX=2 to improve the SNR. The other imaging parameters were FOV= 210 × 210 mm, matrix size = 256 × 148 with partial Fourier oversampling of 20 lines, slice thickness= 4 mm and TE = 84 ms.
Data from 3 slices of this acquisition ( 3 × 60 × 2 = 360 datasets) distributed uniformly throughout the brain were used for training purposes of our experiments and the fourth slice was used as the testing data. Note that the phase errors associated with the various slices are very distinct due to the cardiac, pulsatile and respiratory motion affecting the different slices of the brain differently. Hence, the phase errors of the testing slice can be expected to be very different from the training slices, thus providing a valid test case for our experiments.
The model was trained with 5-layer CNN having 64 convolution filters of size 3 × 3 in each layer. The real and imaginary components of complex data were considered as channels in the denoising step whereas the data-consistency block worked explicitly with complex data. The training was performed for approximately two hours.
Fig. 2 shows a sample DWI reconstructed using various methods from the testing slice. The uncorrected reconstruction of the slice shows severe phase artifacts which is corrected to some extent by the MUSE method. The MUSSELS method provide a better reconstruction compared to MUSE. The MUSSELS reconstruction corresponding to the training slices were fed to MoDL-MUSSELS for deep learning. The resulting learned reconstruction for the testing slice is also shown in Fig 2. It is noted that the MoDL-MUSSELS reconstruction for the test slice is comparable to that of the MUSSELS reconstruction.
Table 1 shows the time taken by the proposed MoDL-MUSSELS and MUSSELS algorithm. Note that the computational complexity of MoDL-MUSSELS is around 450 fold lower than MUSSELS. The greatly reduced runtime is expected to facilitate the deployment of the proposed algorithm on clinical scanners.
Table 1.
Testing time in seconds to reconstruct one average of a single slice with 60 directions and 4 shots. MUSSELS was runs on CPUs with parallel processing.
| Algorithm: | MUSSELS | MoDL-MUSSELS |
|---|---|---|
| Time (sec): | 2700 | 6 |
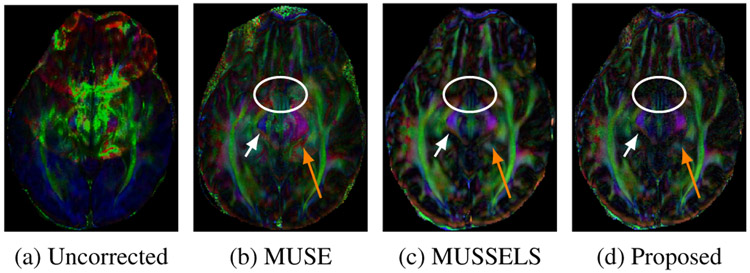
To further validate the reconstruction accuracy of all the DWIs corresponding to the test slice, we performed a tensor fitting using all the DWIs and compared the resulting fractional anisotropy (FA) maps and the fiber orientation maps. For this purpose, the DWIs reconstructed using various methods from the test slice were fed to a tensor fitting routine (FDT Toolbox, FSL ). FA maps were computed from the fitted tensors and the direction of the primary eigenvectors of the tensors was used to estimate the fiber orientation. The FA maps generated using the various reconstruction methods are shown in Fig. 3, which has been color-coded based on the fiber direction. It is noted that these fiber directions reconstructed by the MUSSELS method and the MoDL-MUSSELS match the true anatomy known for this brain region from a DTI white matter atlas.
Fig. 3.
The color-coded FA maps corresponding to various reconstructions from the testing slice. The fiber orientation along the left-right, anterior-posterior and inferior-superior directions are color-coded using red, green and blue colors, respectively. Proposed MoDL-MUSSELS show comparable recovery of fiber orientations to MUSSELS.
4. CONCLUSIONS
We introduced a model based deep learning framework for the compensation of phase errors in multishot diffusion-weighted MRI data. The proposed scheme alternates between CNN denoisers and conjugate gradient optimization algorithm to enforce data consistency. The CNN parameters are learned from exemplary data. The preliminary experiments show that the proposed scheme can yield the state-of-the-art results, while offering several orders of magnitude reduction in run-time.
Acknowledgments
This work is supported by NIH 1R01EB019961-01A1. H.K. Aggarwal acknowledges the Young Stars Estes travel award.
5. REFERENCES
- [1].Chen Nan-kuei, Guidon Arnaud, Chang Hing-Chiu, and Song Allen W, “A robust multi-shot scan strategy for high-resolution diffusion weighted mri enabled by multiplexed sensitivity-encoding (muse),” Neuroimage, vol. 72, pp. 41–47, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Mani Merry, Jacob Mathews, Kelley Douglas, and Magnotta Vincent, “Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS),” Mag. Reson. in Med, vol. 78, no. 2, pp. 494–507, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Aggarwal Hemant K, Mani Merry P, and Jacob Mathews, “Modl: Model based deep learning architecture for inverse problems,” IEEE Trans. Med. Imag, pp. 1–1, 2018, 10.1109/TMI.2018.2865356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Adler Jonas and Öktem Ozan, “Learned primal-dual reconstruction,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1322–1332, 2018. [DOI] [PubMed] [Google Scholar]
- [5].Lee Juyoung, Han Yoseob, and Ye Jong Chul, “k-space deep learning for reference-free epi ghost correction,” arXiv preprint arXiv:1806.00153, 2018. [DOI] [PubMed] [Google Scholar]
- [6].Morrison Robert L, Jacob Mathews, and Do Minh N, “Multi-channel estimation of coil sensitivities in parallel mri,” in IEEE Int. Symp. Bio. Imag IEEE, 2007, pp. 117–120. [Google Scholar]
- [7].Ongie Gregory, Biswas Sampurna, and Jacob Mathews, “Con-vex recovery of continuous domain piecewise constant images from non-uniform Fourier samples,” IEEE Trans. Signal Process, vol. 66, no. 1, pp. 236–250, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]