Abstract
Deep learning methods are emerging as powerful alternatives for compressed sensing MRI to recover images from highly undersampled data. Unlike compressed sensing, the image redundancies that are captured by these models are not well understood. The lack of theoretical understanding also makes it challenging to choose the sampling pattern that would yield the best possible recovery. To overcome these challenges, we propose to optimize the sampling patterns and the parameters of the reconstruction block in a model-based deep learning framework. We show that the joint optimization by the model-based strategy results in improved performance than direct inversion CNN schemes due to better decoupling of the effect of sampling and image properties. The quantitative and qualitative results confirm the benefits of joint optimization by the model-based scheme over the direct inversion strategy.
Index Terms: sampling, deep learning
1. INTRODUCTION
The slow acquisition rate is a primary limitation of magnetic resonance imaging (MRI) over other medical imaging modalities. Image recovery from heavily under-sampled measurements has witnessed extensive research in the past decade that has enabled dramatic reductions in the scan time. The quality of images recovered using computational algorithms heavily depends on the specific image property (e.g., sparsity, low-rank) as well as specific sampling pattern. The general practice is to use variable-density sampling patterns with high incoherence, based on the theoretical compressed sensing results. The optimization of the sampling patterns to recover images with specific properties has been a long-standing problem in MRI.
Several researchers have considered the optimization of sampling patterns assuming different image constraints, including known image support [1], parallel MR acquisition [2], and transform-domain sparsity [3, 4]. These methods can be broadly classified as reconstruction algorithm-dependent and algorithm-independent. For instance, the approaches [1–4] assume a specific image property and optimize the sampling patterns to improve the diversity of measurements for that class. The selection is independent of any specific image reconstruction algorithm or its hyper-parameters. By contrast, [5, 6] considers the optimization of the sampling pattern assuming specific reconstruction algorithms (e.g., TV or wavelet sparsity) for a class of exemplar images. These algorithms utilize a subset of discrete sampling locations using greedy or sparse optimization strategies so as to minimize the reconstruction error using a specific algorithm. The main challenge with these methods is the slow reconstruction algorithm, which restricts the optimization of the pattern to a large class of images. Further, these methods assume fixed reconstruction algorithm and its hyper-parameters during the optimization process.
Machine learning algorithms are now emerging as powerful alternatives for compressed sensing. These methods use learned-models instead of handcrafted priors such as transform-domain sparsity to recover the images. The non-linear convolutional neural networks (CNN) used in these schemes are far more efficient in capturing the non-linear redundancies that exist in images compared to the classical priors. The reconstruction performance of machine-learned models is not dependent on the incoherence of sampling patterns, as hinted by early studies [7].
The study of the dependence of the optimal sampling pattern on a specific network architecture is hence a key problem in deep learning based image recovery. Since the specific image property exploited by CNN approaches is not well understood, it is difficult to adapt the algorithm-independent optimization strategies (e.g., [1–4]) to this setting. At the same time, the fast reconstruction offered by machine learning algorithms makes it possible to extend the algorithm-dependent strategies (e.g., [6]) to a large class of images. Further, the learnable nature of the reconstruction algorithms can adapt its parameters to the sampling pattern.
The main focus of this work is to optimize for the sampling pattern jointly with the deep learned reconstruction algorithm to obtain the best performance over a class of images. The joint optimization strategy is expected to provide improved performance compared to the classical pseudo-random patterns as well as optimization strategies that learn the sampling pattern while assuming the algorithm and its hyperparameters to be fixed. Since the joint optimization problem is non-convex, it may be challenging to achieve the global minimum of the cost function. While the ability of stochastic gradient descent to achieve good performance in CNN training is reported, its use in the proposed setting is not studied. We study the utility of the proposed strategy with both direct inversion [8–10] and model-based methods [7,11].
The CNN based direct inversion schemes [8, 9] require fine-tuning according to a specific sampling pattern. The strong coupling between CNN parameters and the sampling pattern can make the optimization task more challenging. By contrast, model-based schemes use the information of the sampling pattern within the reconstruction algorithm, thus decoupling the CNN block from changes in sampling pattern. This improved decoupling between the parameters in model-based approaches is expected to offer improved performance. This work focuses on the single-channel MRI acquisition setting for simplicity while the future work will consider its extension to multichannel setting.
2. METHOD
2.1. Image Formation & Reconstruction
We consider the recovery of the complex image from its possibly non-Cartesian Fourier samples:
| (1) |
Here, Θ is a set of sampling locations and n[i] is the noise process. The mapping can be compactly represented as . A common approach for recovering images from heavily undersampled measurements such as (1) is model based strategies, which pose the reconstruction as an optimization problem of the form
| (2) |
Here, is a regularization penalty (e.g transform domain sparsity, when with Φ denoting the parameters of the regularizer and the transform. The notation for the solution of (2) denotes its dependence on the regularization parameters as well as sampling pattern.
2.2. Deep learning based image recovery
Recently, several authors have proposed to replace the above hand-crafted image regularization penalties in (2) with learned priors. For instance, model based deep learning (MoDL) [11] formulates the image recovery as
| (3) |
where is a residual learning based CNN that is designed to denoise x. The optimization problem specified by (3) is solved using an iterative algorithm, which alternates between and a data-consistency step , which is implemented using a conjugate gradients algorithm. This iterative algorithm is unrolled to obtain a deep network , where the weights of the CNN blocks and data consistency blocks are shared across iterations as shown in Fig. 1. Specifically, the solution to (3) is given by
| (4) |
Fig. 1.
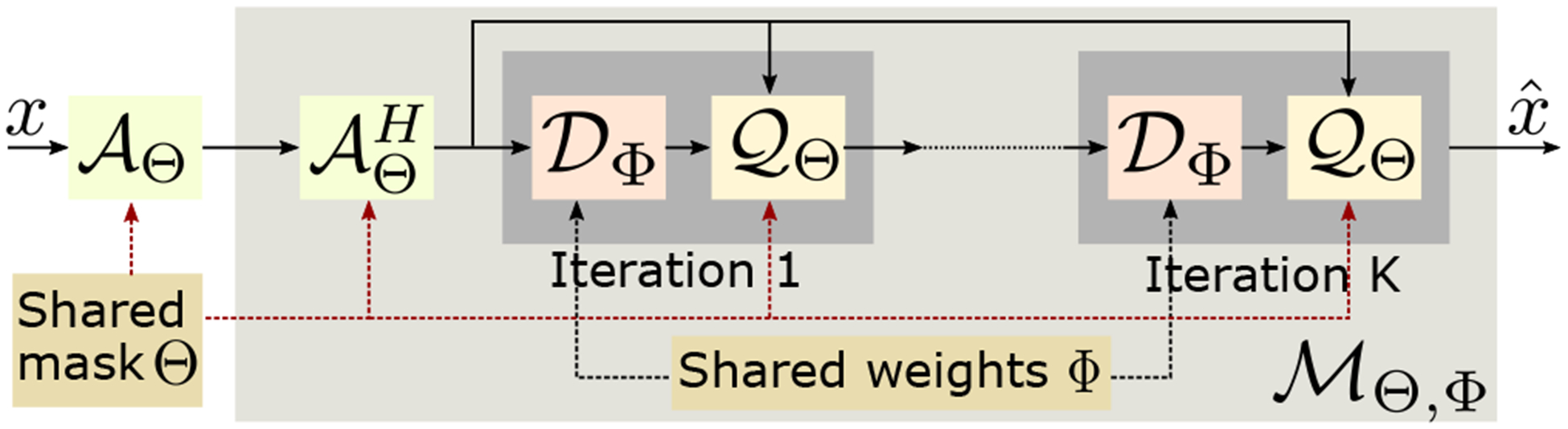
The proposed joint model based deep learning (J-MoDL) architecture and the training process. Each iteration consists of a CNN block and a data-consistency block . This architecture facilitates the decoupling of the image priors and the sampling pattern, thus allowing efficient optimization of the parameters Φ and Θ.
The parameters of the unrolled deep network are learned from a set of training images xi; i = 1, .., N, such that the training error
| (5) |
is minimized. An alternative to the above model-based strategy is direct inversion, which relies on a deep CNN to recover the images from ; the CNN learns to invert the class of images for the specific sampling pattern Θ. The key difference between this strategy and MoDL is the strong coupling between the CNN blocks and the sampling pattern; the CNN parameters need to be fine tuned to the specific sampling pattern. By contrast, the CNN parameters in MoDL are more decoupled from the sampling pattern, making the training easier. We note that the use of within the network enables MoDL to use the same learned DΦ block for different sampling patterns [11].
2.3. Joint Optimization
The main focus of this work is to jointly optimize both and blocks in the MoDL framework with the goal of improving the reconstruction performance. Specifically, we propose to jointly learn the sampling pattern Θ and the CNN parameter Φ from training data using
| (6) |
This proposed J-MoDL framework can be generalized to other error metrics such as perceptual error.
2.4. Parametrization of the sampling pattern
In this work, we restrict our attention to the optimization of the phase encoding locations in MRI, while the frequency encoding direction is fully sampled. Mathematically, we model the sampling set as the translates of a single pattern Γ.
| (7) |
Here Θ = {θi; i = 1, .., P} are the P phase encoding locations, while Γ is the set of samples on a line. In addition to reducing the parameter space, this approach also simplifies the implementation; the blocks can be implemented analytically in-terms of 1-D Fourier transforms. Note that this framework can be generalized to sample arbitrary trajectories (e.g. radial lines with arbitrary angles).
2.5. Network details and Initialization
The J-MoDL reconstruction network is shown in Fig. 1. In our experiments, we observe that a three iteration unfolding was sufficient in the single-channel setting. As seen from [11], more iterations are needed in the multichannel setting. The sampling operator is implemented using a 1-D discrete Fourier transform from the spatial locations to the continuous domain Fourier samples specified by Θ. The data-consistency block is implemented using conjugate gradients algorithm. The CNN block consists of a UNET with four pooling and unpoolong layers. The parameters of the blocks and are optimized to minimize (6).
We utilized publically available knee dataset in [7]. The training data constituted of 381 slices from 10 subjects, whereas test data had 80 slices from 2 subjects. A coil combination was performed to simulate single-coil images. For comparison, we also study the optimization of the sampling pattern in the context of direct inversion (i.e, when a UNET is used for image inversion). A UNET with same number of parameters was used in the study.
In our experiments, we trained the UNET and MoDL architecture with different random sampling masks to make the CNN parameters Φ relatively insensitive to the undersampling patterns. These CNNs were used as the initialization for the networks in the remaining experiments. Starting with this initialization, we first optimize for the sampling pattern Θ alone while keeping the reconstruction frameworks fixed. Second, we simultaneously optimized both the sampling patter Θ and the network parameters Φ in the two frameworks (UNET and MoDL).
3. EXPERIMENTS AND RESULTS
The results of the optimization are reported in Table 1, where we have reported the average PSNR and SSIM values obtained on the test data. The top row corresponds to the optimization of the network parameters Φ alone, assuming incoherent undersampling patterns. The MoDL framework provides an approximate 3.5 dB improvement in performance over a UNET scheme with the same number of parameters. The second row corresponds to the optimization of the sampling pattern Θ alone, while the network parameters are fixed as the above initialization. We note that the optimization of the sampling pattern provided a 1.5 dB improvement in performance with MoDL, while the performance of the UNET degraded. This deterioration is likely due to the close coupling between the UNET parameters and the sampling pattern in direct inversion schemes; when the sampling pattern differs from the ones that were used to train the UNET, it is not guaranteed to yield good performance. The last row corresponds to the joint optimization scheme, where both Θ and Φ are trained. The resulting J-MoDL scheme offers a 0.6 dB improvement in performance over the optimization of Θ alone, while the resulting J-UNET approach provides a 0.6 dB improvement over the initialization. The results demonstrate the benefit of the decoupling of sampling pattern and CNN parameters offered by MoDL in the joint optimization.
Table 1.
The average PSNR (dB) and SSIM values obtained over the test data of two subjects with total of 80 slices using different optimization strategies.
| PSNR | SSIM | |||
|---|---|---|---|---|
| Optimization | UNET | MoDL | UNET | MoDL |
| Φ alone | 30.00 | 33.42 | 0.84 | 0.85 |
| Θ Alone | 25.40 | 35.03 | 0.71 | 0.89 |
| Θ, Φ Joint | 30.61 | 35.69 | 0.87 | 0.90 |
Figure 2 shows the visual comparison of the reconstruction quality obtained by the joint optimization with UNET as well as the MoDL based strategies. The proposed J-MoDL method provides significantly improved results, as highlighted by the zoomed region.
Fig. 2.
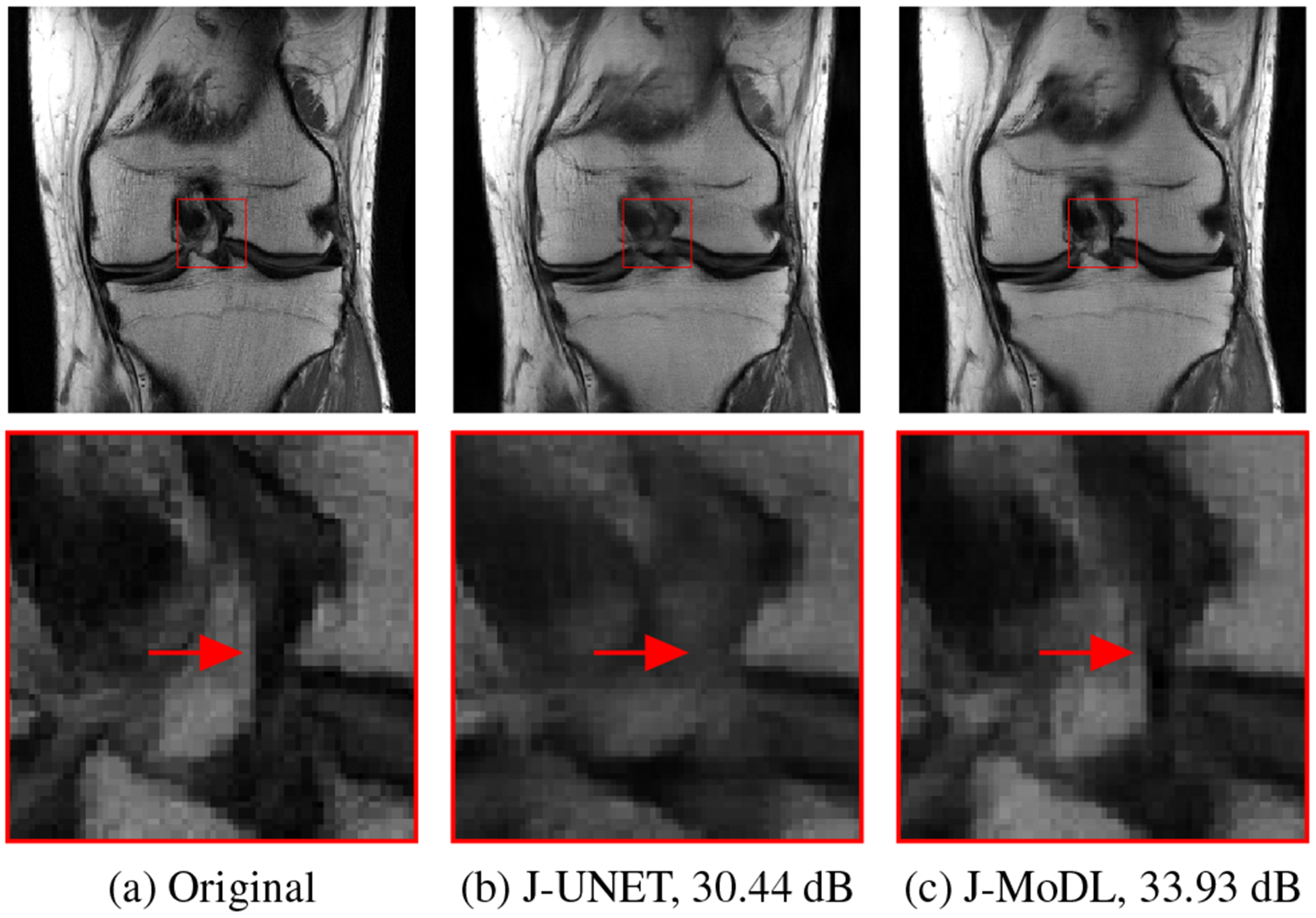
A visual comparison of the J-UNET and the J-MoDL approaches on a test slice. The joint learning using J-MoDL preserves the fine details as pointed by arrows in the zoomed area.
Figure 3 demonstrates the benefits of performing joint optimization of both the sampling pattern and the network parameters as compared to the network alone. The red arrows clearly show that the proposed J-MoDL architecture preserves the high-frequency details better than the MoDL architecture. Figure 4(b) shows the learned sampling mask by the J-MoDL approach while the initialization was done using the mask in Figure 4(a). The learned continuous values were rounded to nearest integer for display purpose.
Fig. 3.
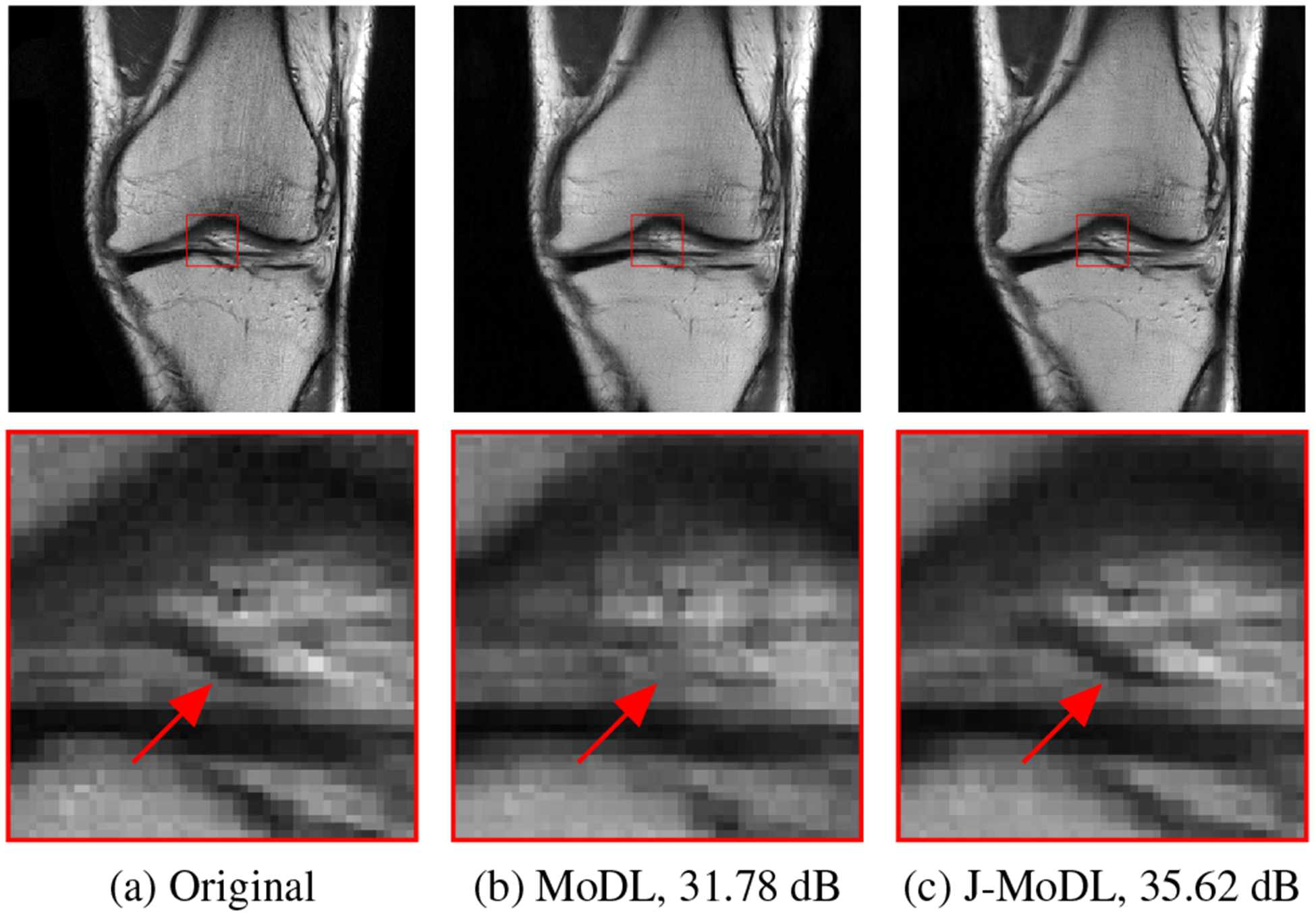
A visual comparison of the MoDL and the J-MoDL approachs shows that the joint optimization preserves the fine structures as shown by arrows.
Fig. 4.

The fixed mask used during testing and the learned mask using the J-MoDL approach. The learned phase encoding locations are continuous-valued that were discretized for display purposes.
4. CONCLUSIONS
This work shows how to jointly optimize the sampling pattern and the reconstruction network simultaneously while obeying the physics of MR acquisition. The proposed joint model-based deep learning framework (J-MoDL) has decoupled sampling and CNN blocks. This decoupling makes J-MoDL architecture relatively insensitive changes in sampling pattern as compare to a direct inverse based method. The experimental results show that the proposed J-MoDL produces better results than J-UNET architecture for the same acceleration factor.
5. REFERENCES
- [1].Gao Yun and Reeves Stanley J, “Optimal k-space sampling in mrsi for images with a limited region of support,” IEEE Trans. Med. Imag, vol. 19, no. 12, pp. 1168–1178, 2000. [DOI] [PubMed] [Google Scholar]
- [2].Xu D, Jacob M, and Liang ZP, “Optimal sampling of k-space with cartesian grids for parallel MR imaging,” in Proc Int Soc Magn Reson Med, 2005, vol. 13, p. 2450. [Google Scholar]
- [3].Levine Evan and Hargreaves Brian, “On-the-fly adaptive k-space sampling for linear MRI reconstruction using moment-based spectral analysis,” IEEE Trans. Med. Imag, vol. 37, no. 2, pp. 557–567, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Haldar Justin P and Kim Daeun, “OEDIPUS: An experiment design framework for sparsity-constrained MRI,” IEEE Trans. Med. Imag, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Sherry Ferdia, Benning Martin, De los Reyes Juan Carlos, Graves Martin J, Maierhofer Georg, Williams Guy, Schönlieb Carola-Bibiane, and Ehrhardt Matthias J, “Learning the sampling pattern for MRI,” arXiv preprint arXiv:1906.08754, 2019. [DOI] [PubMed] [Google Scholar]
- [6].Gözcü Baran,¨ Mahabadi Rabeeh Karimi, Li Yen-Huan, Ilıcak Efe, Çukur Tolga, Scarlett Jonathan, and Cevher Volkan, “Learning-based compressive MRI,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1394–1406, 2018. [DOI] [PubMed] [Google Scholar]
- [7].Hammernik Kerstin, Klatzer Teresa, Kobler Erich, Recht Michael P., Sodickson Daniel K., Pock Thomas, and Knoll Florian, “Learning a Variational Network for Reconstruction of Accelerated MRI Data,” Magnetic resonance in Medicine, vol. 79, no. 6, pp. 3055–3071, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Chen Hu, Zhang Yi, Kalra Mannudeep K., Lin Feng, Chen Yang, Liao Peixo, Zhou Jiliu, and Wang Ge, “Low-Dose CT with a Residual Encoder-Decoder Convolutional Neural Network,” IEEE Trans. Med. Imag, vol. 36, no. 12, pp. 2524–2535, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Han Yoseob, Sunwoo Leonard, and Jong Chul Ye, “k-space deep learning for accelerated mri,” IEEE Trans. Med. Imag, 2019. [DOI] [PubMed] [Google Scholar]
- [10].Bahadir Cagla Deniz, Dalca Adrian V, and Sabuncu Mert R, “Learning-based optimization of the under-sampling pattern in mri,” in International Conference on Information Processing in Medical Imaging. Springer, 2019, pp. 780–792. [Google Scholar]
- [11].Aggarwal Hemant K, Mani Merry P, and Jacob Mathews, “MoDL: Model based deep learning architecture for inverse problems,” IEEE Trans. Med. Imag, vol. 38, no. 2, pp. 394–405, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]


