Abstract
Elastic degree of anisotropy (DoA) is a diagnostically relevant biomarker in muscle, kidney, breast, and other organs. Previously, elastic DoA was qualitatively assessed as the ratio of peak displacements (PD) achieved with the long-axis of a spatially asymmetric Acoustic Radiation Force Impulse (ARFI) excitation point spread function (PSF) aligned along versus across the axis of symmetry (AoS) in transversely isotropic materials. However, to better enable longitudinal and cross-sectional analyses, a quantitative measure of elastic DoA is desirable. In this study, qualitative ARFI PD ratios are converted to quantitative DoA, measured as the ratio of longitudinal over transverse shear elastic moduli, using a model empirically derived from Field II and finite element method (FEM) simulations. In silico, the median absolute percent error (MAPE) in ARFI-derived shear moduli ratio (SMR) was 1.75%, and predicted SMRs were robust to variations in transverse shear modulus, Young’s moduli ratio, speed of sound, attenuation, density, and ARFI excitation PSF dimension. Further, ARFI-derived SMRs distinguished two materials when the true SMRs of the compared materials differed by as little as 10%. Experimentally, ARFI-derived SMRs linearly correlated with the corresponding ratios measured by Shear Wave Elasticity Imaging (SWEI) in excised pig skeletal muscle (R2 = 0.91, MAPE = 13%) and in pig kidney, in vivo (R2 = 0.99, MAPE = 5.3%). These results demonstrate the feasibility of using the ARFI PD to quantify elastic DoA in biological tissues.
Index Terms—: Anisotropy, ARFI, ultrasound elastography, shear wave, muscle, kidney
I. Introduction
The mechanical properties of soft tissues largely depend on the microscopic and macroscopic organization of their building blocks (i.e., fat, collagen, etc) [1]. Therefore, alterations in tissue structure and composition, such as those arising from disease and injury, are detectable by evaluating tissue mechanical properties. Both ultrasound elastography (UE) [2] and magnetic resonance elastography (MRE) [3] are used to measure the mechanical properties of soft tissues. Comparing these two imaging modalities, UE is beneficial in many cases because it is lower cost, real-time realizable, and readily accessible.
For assessing mechanical properties, tissues are assumed generally as isotropic, or that mechanical properties do not vary with direction [2]. However, the isotropic assumption does not hold [4] for many tissues, including muscle [5], tendon [6], kidney [7], and breast [8], which have organized structures. In these anisotropic tissues, mechanical properties vary with direction, and, hence, UE measurements depend on the orientation of the transducer relative to the material structure. If transducer orientation is not properly controlled, anisotropy confounds mechanical property assessments [9]–[11]. On the contrary, if transducer orientation is properly considered, the mechanical degree of anisotropy (DoA) can be exploited as a biomarker for diagnosing and monitoring diseases. For example, it has been demonstrated that malignant and aggressive breasts cancers have higher DoA than benign tumors [12], [13]; the DoA of lower limb muscles was higher in boys with versus without Duchenne muscular dystrophy [14]; and blood pressure modulation and renal inflammation and fibrosis changed DoA of renal medulla and cortex [7], [9], [15]–[17].
Mechanical DoA can be assessed by modeling tissue as a transversely isotropic (TI) material [4], [18], [19]. The TI model, the simplest anisotropic material model, is defined by a plane of isotropy (PoI) perpendicular to an axis of symmetry (AoS). Mechanical properties are the same in the PoI but different along versus across the AoS. Then, elastic DoA can be defined as the ratio of longitudinal (L, indicating the direction along the AoS) over transverse (T, indicating the direction across the AoS) Young’s or shear elastic moduli. In this manner, the ratio of shear moduli derived from shear wave velocities measured in longitudinal versus transverse directions has been used to assess shear elastic DoA [4], [12], [13]. Note that throughout this manuscript, shear elastic DoA and shear elastic moduli ratio are considered synonymous.
Although DoA can be assessed using shear wave approaches, the associated need to monitor shear wave propagation over a lateral range spanning millimeters outside of the region of excitation (ROE) limits applications in deep tissues and/or in stiff tissue because low ARF magnitudes yield low amplitude shear waves that quickly attenuate below measurement sensitivity outside of the ROE. This, combined with a loss of resolution due to spatial averaging and the confounding effects of out-of-plane shear wave reflections/distortions that can arise over the shear wave propagation distance, suggests the relevance of alternative DoA assessment methods that operate along the same A-line as, or “on-axis” with, the ARF excitation.
More recently, Hossain et al. developed a novel method to assess the DoA of mechanical properties in TI materials using ARFI-induced PD [17]. In this approach, DoA is assessed as the ratio of PDs achieved when the long axis of a spatially asymmetric ARF excitation PSF is aligned along versus across the AoS [17]. The advantage of this method is that DoA is assessed in the ARF ROE without observing shear wave propagation, so measurements are less susceptible to error due to shear wave attenuation and tissue inhomogeneities. The investigators applied this method to assess mechanical anisotropy in vivo in the human renal cortex [7], [15]–[17], and muscle [20], [21].
While it has been shown that ARFI PD ratios (PDRs) are proportional to shear moduli ratios (SMRs) in TI materials, PDRs are qualitative. The objective of this work is to achieve quantitative DoA measurement by empirically deriving a relationship between measured ARFI PDR and true SMRs [21] using the finite element method (FEM) and Field II simulations [22]–[25]. The robustness of the derived empirical model is examined in silico over a range of elasticities, acoustic properties, ARF PSF dimensions, and material densities. Finally, the derived empirical model is demonstrated for quantifying SMR ex vivo in pig skeletal muscles and in vivo pig renal medulla and cortex.
II. Materials and Methods
A. In Silico Model
The in silico model developed by Palmeri et al. [24], [25], was adapted to simulate ARFI imaging of an elastic TI solid using Field II [22], [23] and LS-DYNA3D (Livermore Software Technology Corp. Livermore, CA), a finite element method (FEM) solver. The adapted simulation methods are detailed in [19]. For this work, the ARF field was simulated using the parameters presented in Table I. The simulations were implemented with an FE mesh that spanned 7 to 42 mm, −8 to 8 mm, and −8 to 8 mm, in axial, lateral, and elevational dimensions, respectively. The isotropic element size was 0.2 × 0.2 × 0.2 mm3.
TABLE I.
Parameters Implemented for ARFI and/or SWEI
| Name | Value |
|---|---|
| Beam sequence parameters | |
| Transducer | 9L4 |
| Bandwidth | 55.38% |
| Sampling frequency | 40 MHz |
| Acoustic lens axial focus | 20 mm |
| ARF excitation duration | 300 cycle |
| ARF excitation center frequency | 4.0 MHz |
| ARF excitation F/# | 1.5 |
| Tracking center frequency | 6.0 MHz |
| Tracking transmit F/# | 1.5 |
| Tracking receive F/#* | 0.75 |
| Excitation and tracking focal depth | 20 mm |
| Tracking PRF | 13 KHz |
| Tracking ensemble length | 5.5 ms |
| Acoustic attenuation | 0.5 dBcm−1Mhz−1 |
| Sound speed | 1540 ms−1 |
| Normalized cross correlation parameters | |
| Interpolation factor | 4 |
| Kernel length | 512 μm |
| Search region | 80 μm |
Aperture growth and dynamic Rx focusing enabled
The LS-DYNA3D “MAT_ORTHOTROPIC_ELASTIC” material model was used to simulate TI elastic materials. Although TI elastic materials have five material constants [4], the incompressibility assumption reduced the number of material constants to three [4]: transverse shear modulus (μT), longitudinal shear modulus (μL), and longitudinal to transverse Young’s moduli ratio (YMR, EL/ET), with Poisson’s ratio in the plane of symmetry (νLT) = 0.499 [4], [17]. To derive the empirical relationship between PDR and SMR (μL/μT), different homogeneous, incompressible, linear, elastic, TI materials were simulated by varying μL/μT. Variation of μL/μT was achieved by changing μL and by keeping ET, EL, and μT fixed.
The materials were divided into two groups: train and test sets. For these sets, SMR was varied in steps of 0.25 from 0.15 to 6.65 (train) or 0.25 to 6.5 (test) with EL = 12.8 kPa, ET = 12.2 kPa, μT = 4.0 kPa, νLT = 0.499, and Poisson’s ratios in the plane of isotropy νTT = 0.52. In this manner, μL was varied from 0.6 to 26.6 kPa and YMR (EL/ET) was fixed to 1.05 in both train and test materials. The density (ρ) of all TI materials was fixed to 1.0 gcm−3. Note that train and test data sets were constructed such that no material in the train set had the same SMR as any material in the test set. Thus, empirical model performance was evaluated on materials that were not used to derive the model.
To assess anisotropy, the simulated materials were mechanically excited with the long axis of the ARF excitation PSF (measured in the c-plane at the focal depth) aligned along and then across the material AoS. The resulting FEM displacement estimates were used to direct scatterer motion in Field II simulations of ultrasound radiofrequency (RF) data using the parameters presented in Table I. The Field II simulations implemented 15 scatterers per resolution cell, with 20 independent scatter realizations. Each realization was generated using a unique random distribution of scatterers’ locations. White Gaussian noise was added to each RF line of the test materials using the awgn function in MATLAB (Mathworks Inc., Natick, MA, USA) to simulate system echo SNR of 40 dB to replicate the SNR of typical commercially available clinical ultrasound imaging systems.
Motion tracking was performed by one-dimensional axial normalized cross-correlation using the parameters listed in Table I [26]. After motion tracking, a 2-D (axial × time) dataset describing axial displacements over time was generated for each simulated TI material and each PSF orientation. From the displacement profiles, PD was identified. Then, for each scatterer realization, mean PD over a 3 mm axial range surrounding the focal depth (20 ± 1.5 mm) was measured after removing outliers, which were defined as values outside the 10th to 90th measurement percentiles.
B. Empirical Model Derivation
The derived mean PDs were evaluated as ratios of measurements made with the ARF PSF long-axis aligned along the material AoS (such that the result, denoted PDT, predominantly reflected the transverse shear elastic modulus) versus measurements made with the ARF PSF long-axis aligned across the material AoS (such that the result, denoted PDL, predominantly reflected the longitudinal shear elastic modulus [4], [17]. Because PD is inversely related to elastic modulus, the result (PDT/PDL) reflected μL/μT.
The relationship between PDT/PDL and μL/μT was empirically modeled by fitting a 3rd order polynomial function to the median (across scatterer realizations) PDT/PDL versus true μL/μT in the train materials. Then, the derived empirical model was applied to convert qualitative PDRs to quantitative DoA measures in the test materials and experimental data.
C. In Silico Evaluation of Empirical Model Robustness
The robustness of the derived empirical model to variations in mechanical properties, acoustic attenuation, speed of sound, material density, and ARF PSF dimension was evaluated.
To determine the robustness of the derived empirical model to variations in material constants, their values were varied between the train and test materials. For train materials, μT and EL/ET were fixed to 4 kPa and 1.05, respectively. However, for test materials, μT was varied to 2, 4, or 8 kPa while keeping EL/ET fixed to 1.05 and then, EL/ET was varied to 0.55, 1.5, or 2.0 while keeping μT = 4.0 kPa respectively. These values were selected to generally reflect the known properties of muscle and renal parenchyma [9], [10], [27]–[31].
In addition to mechanical parameters, the robustness of the empirical model to variations in acoustic properties was evaluated. Acoustic attenuation and sound speeds were 0.5 dBcm−1MHz−1 and 1540 ms−1, respectively, for train materials, while for test materials, acoustic attenuation was 0.25, 0.5, or 1.0 dBcm−1MHz−1 and sound speed was 1500, 1540, or 1580 ms−1. These ranges of acoustic attenuation and sound speed values were selected to be consistent with expectations for biological tissues. Note that acoustic attenuation and sound speed values varied in both ARF excitation and tracking pulses.
Beyond mechanical and acoustic properties, complex system inertia may impact empirical model performance. Considering a viscoelastic material as a series of individual mass-spring-damper units that are interconnected in three dimensions, the term “complex system inertia” describes the inertia that evolves as motion propagates from one mass-spring-damper unit to another [32]. The complex system inertia is minimal when the material is excited by an infinitely small point-force such that motion propagation across mass-spring-damper units is negligible [32]. Therefore, the magnitude and spatial expanse of complex system inertia depend on the size of the ARF excitation PSF as well as the mechanical properties and density of the material [32]. Thus, without a priori knowledge of the material properties, complex system inertia is unknown, yet it prolongs ARFI displacement profiles. To investigate the impact of complex system inertia on the described method’s estimates of SMRs, different material densities, and ARF excitation PSF dimensions were implemented between training and test materials, such that the complex system inertia that developed in the training materials was different from that which developed in testing materials.
The material density was 1.0 gcm−3 for train materials and 0.9, 1.0, or 1.1 gcm−3 for test materials. Young’s moduli ratio (1.05), transverse shear modulus (4.0 kPa), acoustic attenuation (0.5 dBcm−1MHz−1), and sound speed (1540 ms−1) were held constant for both train and test materials. To vary the spatial distribution of ARF, a matrix array with 192 × 192 elements was simulated to generate three different ARF focal configurations. The (lateral, elevational) F-numbers were set to (2.50, 4.25) for train materials and to (2.00, 3.40), (2.50, 4.25), and (3.00, 5.10) for test materials. Note that the spatial asymmetry ratio (elevational over lateral span) of the ARF excitation PSFs remained constant (at 1.7) despite differences in the overall ARF excitation PSF size. Although ARF excitation pulse F-numbers varied, both the lateral and elevational F-numbers of tracking pulses were held at 1.5 for train and test sets. A unique empirical model was derived to convert PDRs measured with the simulated matrix array to quantitative shear moduli ratios following the previously-described model derivation methods.
D. Experimental Demonstration: ARFI and SWEI Data Acquisition and Processing
For all experimental studies, ARFI and SWEI data were acquired in immediate succession so that SWEI-derived DoA outcomes could be compared to quantitative ARFI DoA measures. Data were acquired using a Siemens S3000 Helix imaging system with a 9L4 transducer (Siemens Healthineers, Ultrasound Division, Issaquah, WA, USA). The ARFI and SWEI beam sequences were implemented as previously described in [7]; the specific imaging parameters are listed in Table I. ARFI imaging and SWEI [33] were performed ex vivo in the lower limb skeletal muscles of 2 pigs and in vivo in the kidneys of 3 pigs.
For ex vivo muscle imaging, the legs of one female and one male pig (approximately 3 and 6 months old with body weights of 33 and 60 Kg, respectively) were disarticulated at the acetabulofemoral joint after completing terminal protocols under unrelated studies. Legs were kept refrigerated for 24 hours. Then, the legs were removed from the refrigerator and sat at room temperature for 2 hours before being placed in a room-temperature water bath for imaging on a motion isolation table (Newport, Irvine, California, USA). Under B-mode guidance, the tensor fasciae latae (N=1), biceps femoris (N=2), and gluteus superficial (N=2) muscles were interrogated.
For ARFI and SWEI data collection, the transducer was attached to a rotation stage (model: CONEX-NSR1, Newport, Irvine, California, USA) by a custom probe holder to enable precise control of transducer orientation with respect to muscle fiber alignment, where 0° and 90° corresponded to the lateral aspect of the transducer being oriented along and across the muscle fibers, respectively. Note that, for ARFI data acquisitions, aligning the lateral aspect of the transducer along the muscle fibers corresponded to the long-axis of the ARF PSF being oriented across the muscle fibers for PD measures that primarily reflect the longitudinal shear elastic modulus, μL. Similarly, aligning the lateral aspect of the transducer across muscle fibers resulted in PD measures that primarily reflect the transverse shear elastic modulus, μT. For SWEI data acquisitions, orienting the lateral aspect of the transducer along versus across the muscle fibers resulted in the observation of shear wave propagation along versus across muscle fibers, reflecting, μL and μT, respectively. Three repeated acquisitions were performed for each imaging modality by rotating the transducer from 0° to 90° and then bringing the transducer back to 0° before repeating the rotation two more times. The ARFI and SWEI focal depths were, respectively, 15 and 15 mm (tensor fasciae latae); 17 and 20 mm (biceps femoris); and 14 and 20 mm (gluteus superficial). Note that a unique empirical model was generated, using the methods described above, for each focal depth.
In vivo kidney imaging was performed under a protocol approved by the Institutional Animal Care & Use Committee at the University of North Carolina at Chapel Hill. Data were collected in 3 male pigs with an approximate bodyweight of 50–55 kg and the age of 5–6 months at the time of imaging. All pigs were anesthetized and sedated with telazol (2–3mg/kg IM), and respiration was spontaneous throughout the procedures.
The left or right kidney of each pig was chosen randomly and exposed via midline and lateral flank laparotomy incisions and the combination of sharp and blunt dissection. ARFI imaging and SWEI were performed at the superior pole, with the lateral aspect of the transducer oriented along and across nephron alignment in the medulla and cortex. The transducer was attached to a stereotactic clamp and was rotated manually with real-time feedback from an attached gyroscope (MTw Awinda, Xsens Technologies B.V., Netherlands). The imaging focal depth was maintained at 23 mm for all pigs and transducer orientations using acoustic standoff pads (AquaFlex, Civco, Iowa, USA). A unique empirical model was derived for a focal depth of 23 mm using the methods detailed above.
As for the in silico studies, experimental ARF-induced motion was measured by 1-D axial normalized cross-correlation [26] using the parameters listed in Table I. From the resulting displacement profiles, PD was identified and rendered into 2-D parametric PD images. Then, in 3.0 × 3.0 mm (axial × lateral) ROIs centered at the focal depth, median PD was calculated after removing outliers, which were defined as any PD value outside the 10th to 90th percentile value. Finally, PDRs (PDT/PDL) were calculated as the ratios of median PD achieved when the lateral aspect of the transducer was aligned at 90° versus 0° relative to the tissue AoS. These qualitative PDRs were converted to quantitative measures of SMR using the derived empirical models.
From the SWEI data, group shear wave velocity (SWV) was calculated using the methods described in [7], [33], [34]. Briefly, a moving average filter (movmean function in MATLAB) with a window size of 0.5 mm was applied axially to improve displacement SNR, and directional filtering [35] was used to reject right-to-left propagating shear waves. Next, time to peak (TTP) displacement was calculated at each pixel, and SWV was estimated at each pixel by fitting a straight line to lateral location versus TTP in laterally sliding windows of 2.5 mm length. If the R2 of the fit was less than 0.8, the calculated SWV was discarded. Shear modulus was estimated from group SWV(V) as μ = ρV2, where ρ is the density, which was assumed to be 1.0 gcm−3. From these shear modulus estimates, 2-D parametric shear modulus images were rendered, and median shear modulus was calculated (after removing outliers defined as values outside the 10th to 90th percentile values) in the same 3.0 × 3.0 mm (axial × lateral) ROIs used for median PD calculation. Finally, shear moduli ratios (μL/μT) were calculated as the ratio of median shear modulus values achieved with the lateral aspect of the transducer aligned at 0° versus 90° to the tissue AoS.
E. Statistical Analysis
All statistical analyses were carried out using MATLAB (Mathworks Inc., Natick, MA, USA). Using the Kruskal-Wallis test (kruskalwallis function), ARFI-derived SMR for a specific test material were compared across transverse shear moduli (2, 4, and 8 kPa), Young’s moduli ratios (0.55, 1.5, and 2.0), speed of sound (1500, 1540, and 1580 ms−1), attenuations (0.25, 0.5, and 1.0 dBcm−1MHz−1), material densities (0.9, 1.0, and 1.1 gcm−3), and ARF focal configurations (lateral F-number 2.0, 2.5, 3.0 and elevational F-number 3.4, 4.25, and 5.1) parameters. If statistical significance was found, the two-sample Wilcoxon rank-sum test (ranksum function) was used to find the parameter pair that yielded statistically different predicted SMR. The ability to differentiate TI materials by its SMR was evaluated by comparing the predicted SMRs of all possible pairings of the 26 simulated test materials using the Wilcoxon rank-sum test. In this manner, the ability to distinguish materials was evaluated separately for all test set mechanical properties, acoustic attenuations, sound speeds, material densities, and ARF excitation PSF dimensions. Finally, correlations between ARFI- and SWEI-derived SMRs of muscle, ex vivo and kidney, in vivo were evaluated by linear regression. Statistical significance was based on p ≤ 0.05.
III. Results
A. In Silico Performance
Fig. 1(a) shows a plot of PDR (PDT/PDL) versus true SMR (μL/μT) in the simulated train materials. Recall that no noise was added to the simulated RF data for the train materials. The derived empirical model resulting from the 3rd order polynomial fit was:
| (1) |
Fig. 1.
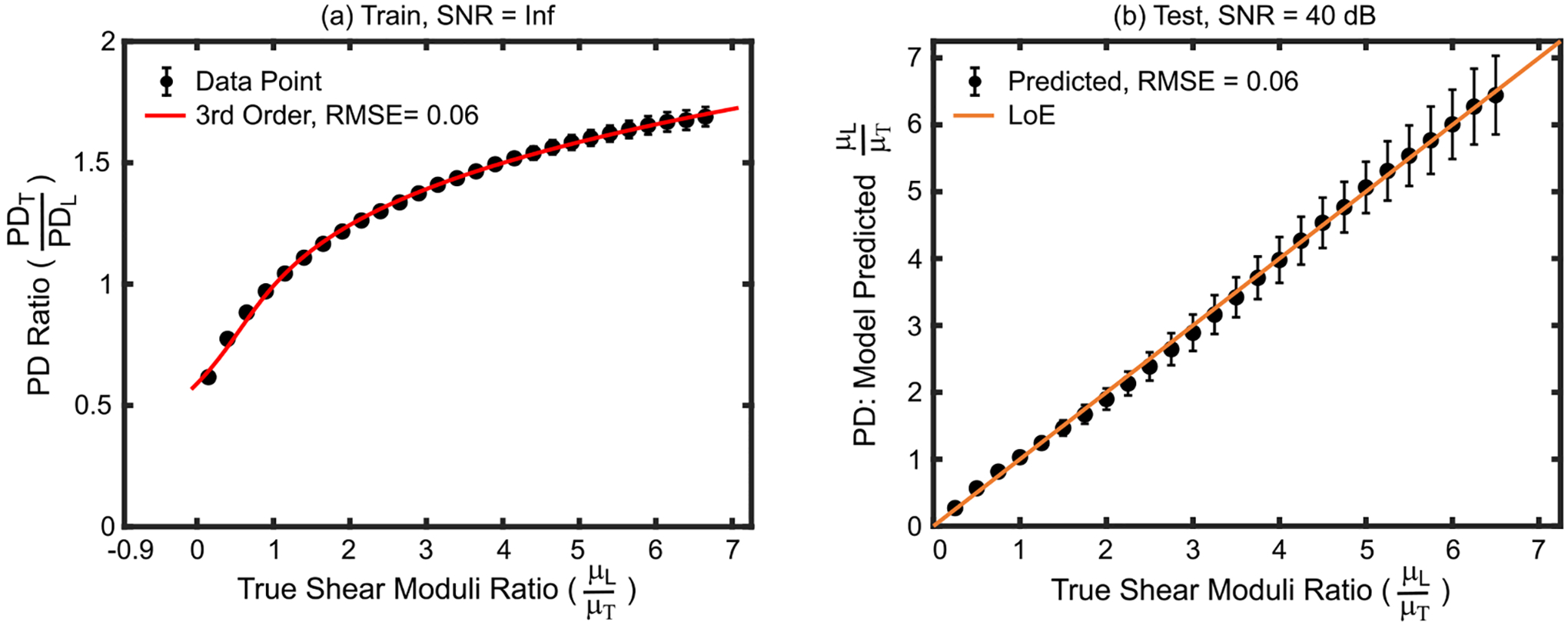
(a) PD ratio versus true shear moduli ratio in the train set materials. The 3rd order polynomial fit (red) indicates the empirical model that was derived to convert qualitative PD ratios to quantitative shear moduli ratios. (b) Shear moduli ratios predicted by the derived empirical model versus true shear moduli ratios for test set materials. Data are plotted as median ± 0.5×interquartile range over 20 independent speckle realizations. LoE = Line of equivalency, RMSE = root mean square error, SNR = signal-to-noise ratio.
Note that SMR and PDR values of 1 are expected for isotropic materials. By Equ. 1, when the PDR equals 1, the predicted SMR also equals 1; however, the fit was not constrained to meet this requirement. Fig. 1(b) shows that, despite adding noise to test materials to simulated a 40 dB system echo SNR, the derived empirical model predicted the SMRs of the test materials with root mean square error (RMSE) of 0.06 and a median absolute percent error (MAPE) of 1.75%.
B. In Silico Performance
Fig. 2 indicates that the empirical model predictions of true SMR are approximately the same whether the YMR (EL/ET, panel (a)) and transverse shear modulus (μT, panel (b)) of test materials were the same (black) or different (magenta and green) from those of the train materials. The Kruskal–Wallis one-way analysis of variance test suggests that predicted SMRs statistically differed from true values for the two materials with true SMRs of 0.25 and 0.50 (panel (a)). For the material with a true SMR of 0.25, the Wilcoxon rank-sum test suggests that predicted SMRs statistically differed between materials with YMRs of 1.05 versus 2.0 (p = 0.03) and 0.55 versus 2.0 (p = 0.003). For the material with 0.50 true SMRs, the predicted SMRs statistically differed between materials with YMRs of 0.55 and 2.0 (p = 0.006). For all test materials, the RMSE was 0.1 and the MAPE was 2.7% and 3.0% for YMRs of 0.55 and 2.0, respectively. When the transverse shear modulus in test materials deviated from that of train materials (panel (b)), the Kruskal–Wallis test suggested no statistical difference between predicted SMRs (p>0.05). For all test materials with μT = 2.0 kPa, the overall RMSE and MAPE were 0.09 and 2.65%, respectively. For test materials with μT = 8.0 kPa, the overall RMSE and MAPE were 0.2 and 5.10%, respectively.
Fig. 2.
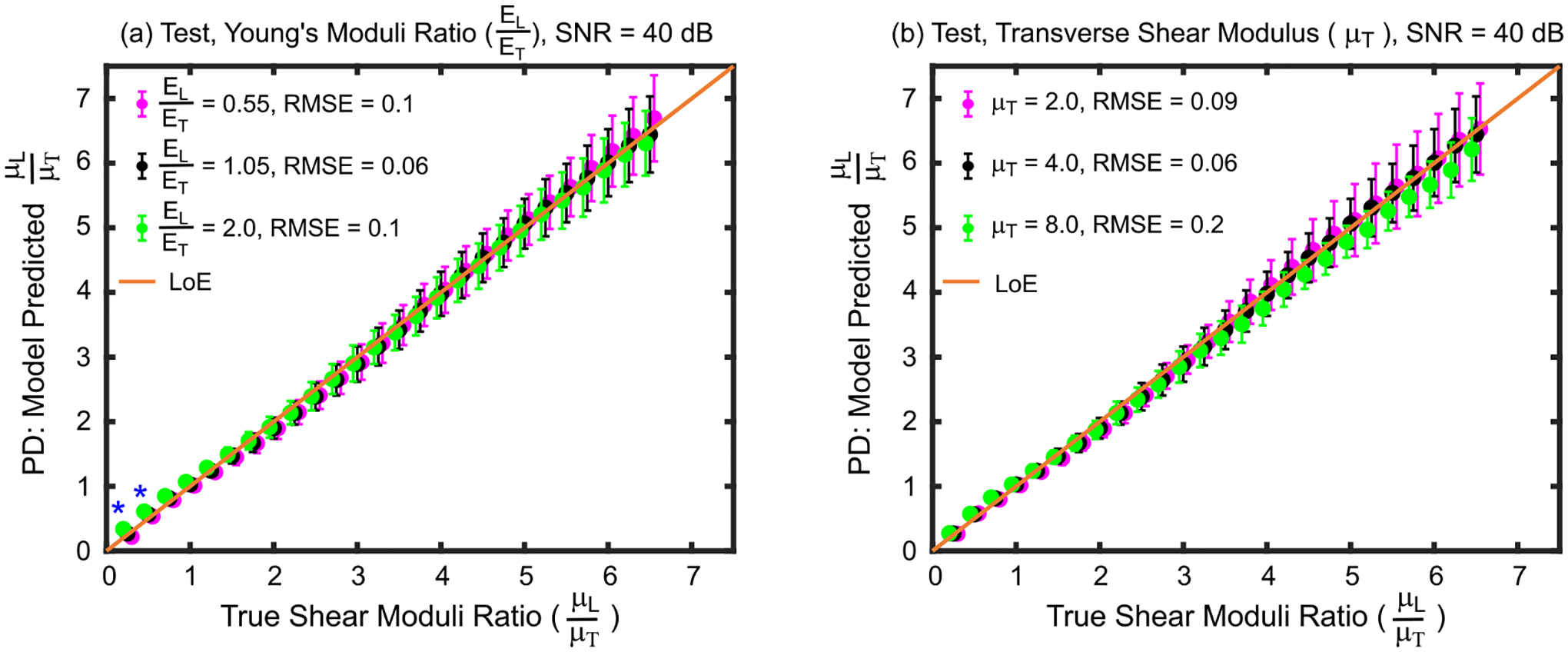
Shear moduli ratios predicted by the derived empirical model versus true shear moduli ratios for test set materials with (a) Young’s moduli ratios and (b) transverse shear modulus values that were lower than (magenta), higher than (green), or the same as (black) those of the train set materials used to derive the model. Asterisks (*) indicate statistical difference between predicted shear moduli ratios across Young’s moduli ratios (Kruskal–Wallis one-way analysis of variance, p<0.05). Data are plotted as median ± 0.5×interquartile range over 20 independent speckle realizations. LoE = Line of equivalency, RMSE = root mean square error, SNR = signal-to-noise ratio.
Agreement between predicted and true SMRs when test set materials had acoustic attenuations and speeds of sound that deviated from the train set materials is shown in Fig. 3. Panel (a) shows that predicted SMRs were not statistically different (Kruskal–Wallis, p>0.05) for any true SMR when acoustic attenuation was varied or kept same between test and train materials. The RMSE and MAPE were 0.13 and 3.0% when the test acoustic attenuation was 0.25 dBcm−1MHz−1 and 0.08 and 2.0% when the acoustic attenuation was 1.0 dBcm−1MHz−1. Panel (b) shows that varying the speed of sound between test and train materials did not result in a statistical difference between predicted SMRs except for the test material with true μL/μT = 0.25 (Kruskal–Wallis, p = 0.03). In this material, predicated SMRs were statistically different between test materials with sound speeds of 1500 versus 1580 ms−1 (Wilcoxon, p = 0.02) and 1540 versus 1580 ms−1 (p = 0.03). The RMSE and MAPE were 0.12 and 2.8%, respectively for the material with a sound speed of 1500 ms−1 and 0.17 and 4.0%, respectively for the material with a sound speed of 1580 ms−1.
Fig. 3.
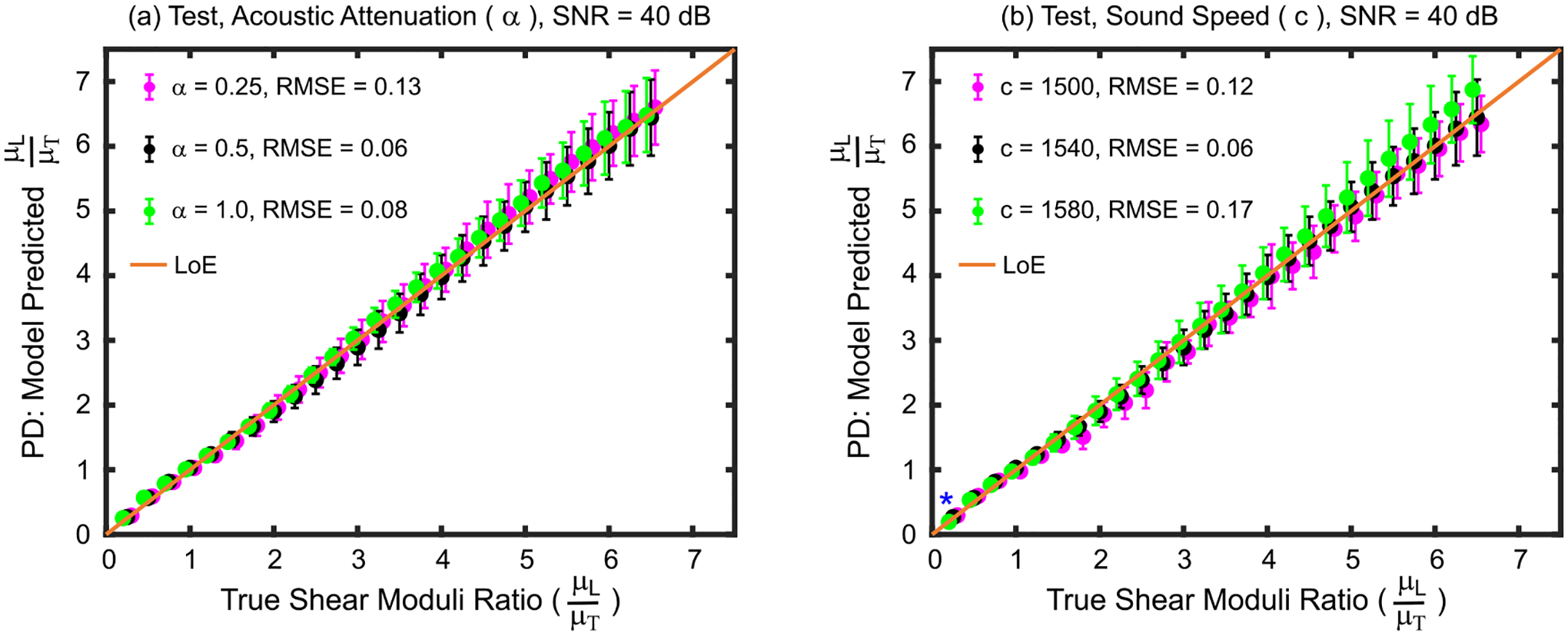
Shear moduli ratios predicted by the derived empirical model versus true shear moduli ratios for test set materials with (a) Young’s moduli ratios and (b) transverse shear modulus values that were lower than (magenta), higher than (green), or the same as (black) those of the train set materials used to derive the model. Asterisks (*) indicate statistical difference between predicted shear moduli ratios across Young’s moduli ratios (Kruskal–Wallis one-way analysis of variance, p<0.05). Data are plotted as median ± 0.5×interquartile range over 20 independent speckle realizations. LoE = Line of equivalency, RMSE = root mean square error, SNR = signal-to-noise ratio.
Fig. 4 shows the agreement between predicted and true SMRs when the train and test materials had different material densities (panel (a)) and were interrogated using ARF PSFs with different dimensions (panel (b)). When material density varied between train and test set materials, the Kruskal–Wallis one-way analysis of variance test suggested that no predicted SMRs statistically differed due to variations in material densities. The (RMSE, MAPE) for materials with densities of 0.9 and 1.1 gcm−3 were (0.09, 2.6%) and (0.09, 2.8%), respectively. When the interrogating ARF PSF dimensions changed, the Kruskal–Wallis test suggested that predicted SMRs statistically differed for the case of true μL/μT = 0.25 (p = 0.02). For this case, the Wilcoxon rank-sum test indicated that the predicated SMR interrogated using an ARF PSF with (lateral, elevational) F-number of (2.0, 3.4) statistically differed from the predicted SMR interrogated using an ARF PSF with (lateral, elevational) F-number of (3.0, 5.1) (p = 0.007). The RMSE and MAPE, for the former were 0.09 and 2.5% and,for the latter were 0.14 and 3.0%.
Fig. 4.
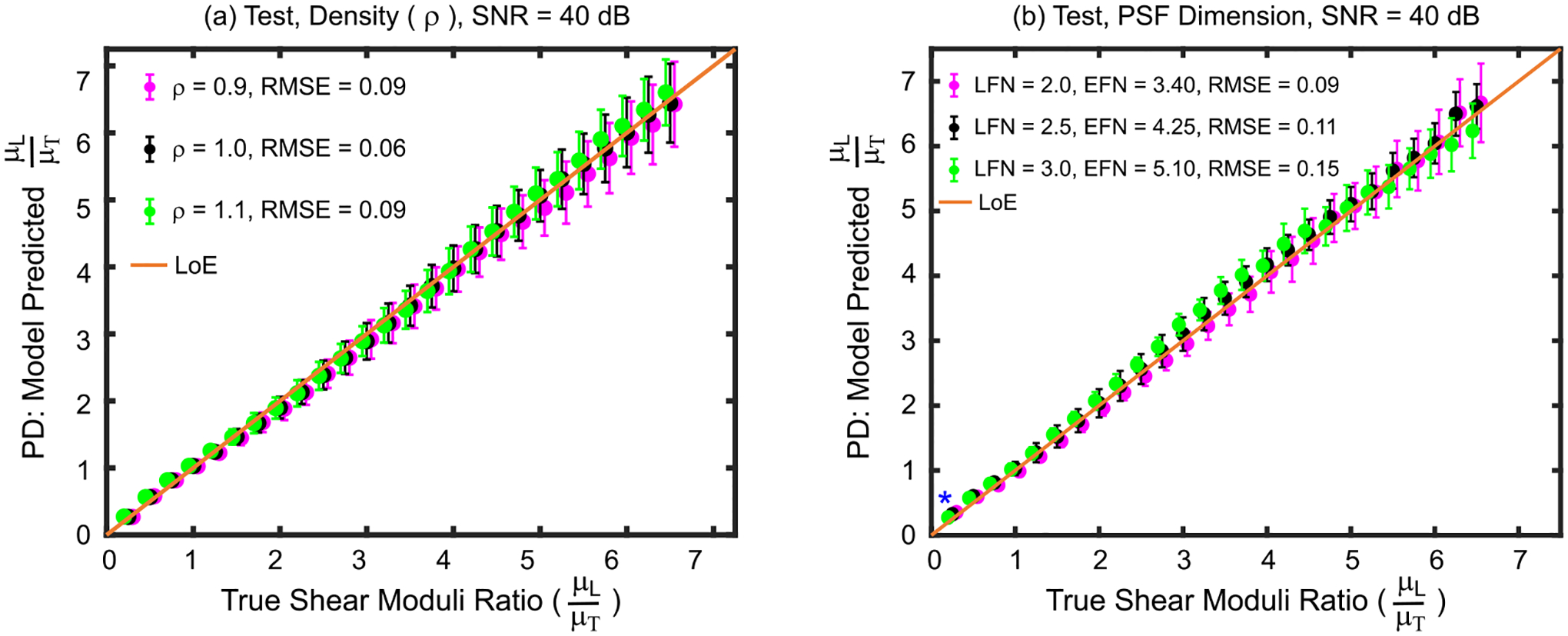
Shear moduli ratios predicted by the derived empirical model versus true shear moduli ratios for test set materials with (a) material densities and (b) ARF focal configurations that were lower than (magenta), higher than (green), or the same as (black) those of the train set materials used to derive the model. Asterisks (*) indicate statistical difference between predicted shear moduli ratios across focal configurations (Kruskal–Wallis one-way analysis of variance, p<0.05). Data are plotted as median ± 0.5×interquartile range over 20 independent speckle realizations. LFN = Lateral F-number, EFN = Elevational F-number, LoE = Line of equivalency, RMSE = root mean square error, SNR = signal-to-noise ratio.
C. Ability to Distinguish Anisotropic Material
Fig. 5 graphically depicts p-values testing the null hypothesis that the predicted SMRs do not differ for all possible pairings of the 26 test materials (Wilcoxon rank-sum test). The blue area indicates p ≤ 0.05, suggesting that the predicted SMRs were statistically different between the associated paired materials, whereas the red area indicates p > 0.05, suggesting that predicted SMRs were not statistically different between the associated paired materials. For example, the predicted SMR of materials with true SMR of 2.5 and 2.75 were not statistically different (p = 0.07), but the predicted SMRs were statistically different for materials with true SMRs of 2.5 and 3.0 (p < 0.05). On average, the empirical model distinguished materials with a greater than 10% difference in true SMR. Note that for this analysis, the TI material mechanical properties, acoustic attenuations, sound speeds, and material densities were the same between the paired materials.
Fig. 5.
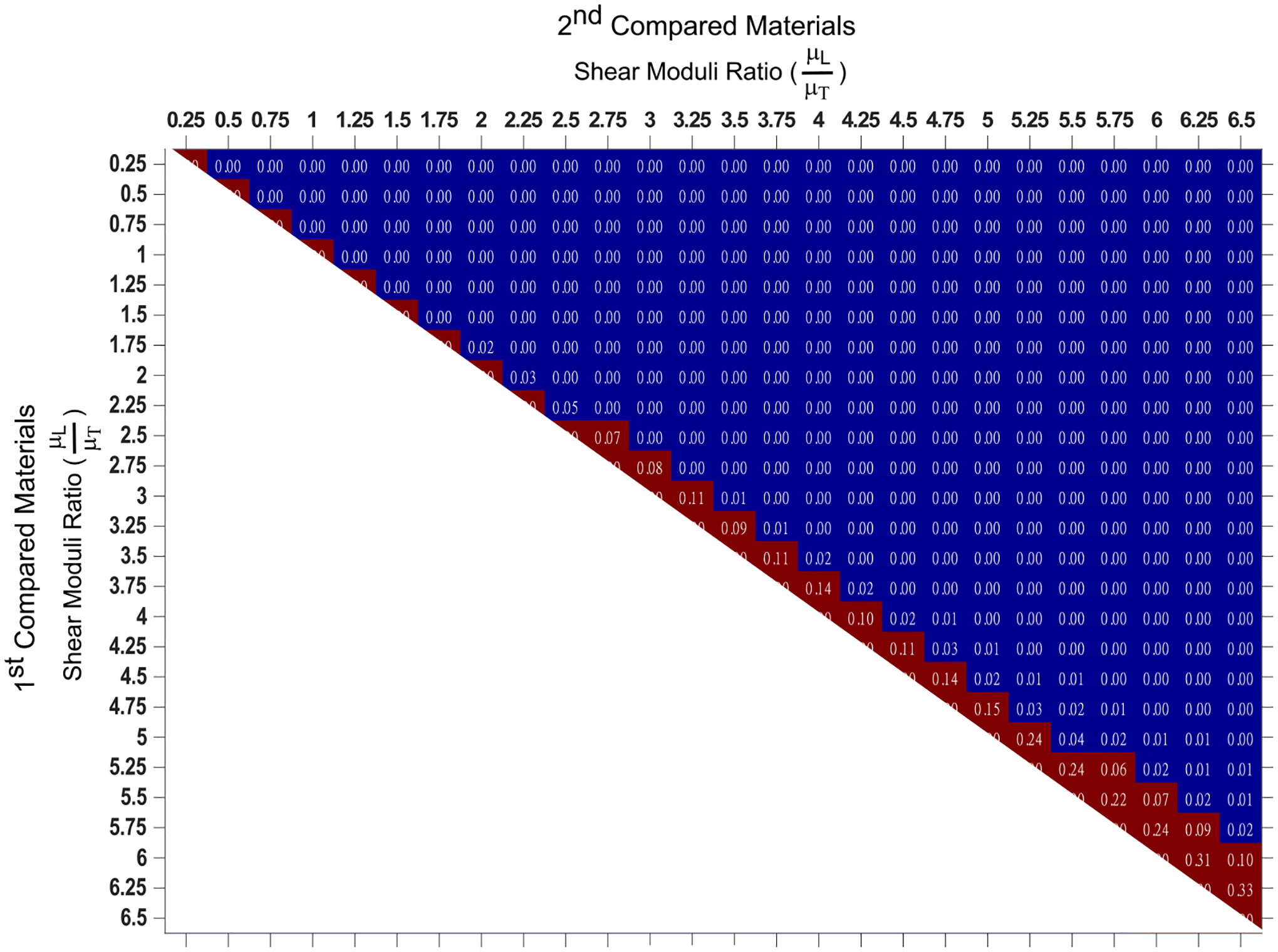
p-values derived by the Wilcoxon rank-sum test evaluating the null hypothesis that predicted shear moduli ratios do not differ for all possible pairings of the 26 test materials. All materials had Young’s moduli ratio, transverse shear modulus, acoustic attenuation, sound speed, and material density of 1.05, 4 kPa, 0.5 dBcm−1MHz−1, 1540 ms−1, and 1 gcm−3, respectively. Blue indicates p ≤ 0.05, and red shows p > 0.05.
Fig. 6, panels (a-e) show the minimum percent difference in true SMRs that are needed to distinguish two compared materials by their predicted SMRs. Each panel shows the result when the material property indicated in the panel title varied between compared materials.
Fig. 6.
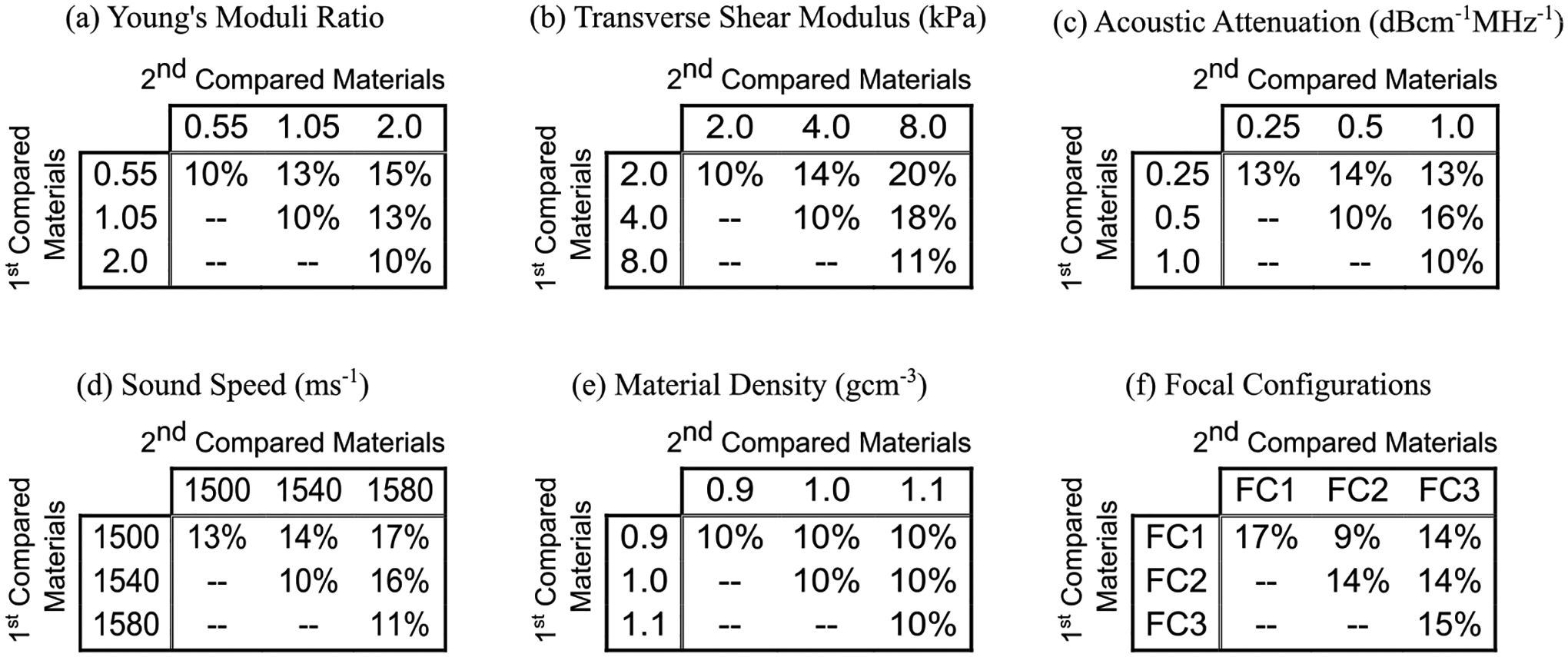
Minimum percent difference in true shear moduli ratios needed to differentiate two TI materials by predicted shear moduli ratios when the compared materials’ (a) Young’s moduli ratios, (b) transverse shear moduli, (c) acoustic attenuations, (d) sound speeds, (e) densities, or (f) ARF excitation PSF dimensions were the same or different. In panel (f), FC1, FC2, and FC3 focal configurations represent (latera, elevational) F-numbers of (2.00, 3.40), (2.50, 4.25), and (3.00, 5.10), respectively. For each panel, the center cell (2nd row, 2nd column) corresponds to the case when the training and test materials had the same properties.
In panel (a), the compared materials have the same transverse shear modulus (4.0 kPa), acoustic attenuation (0.5 dBcm−1MHz−1), sound speed (1540 ms−1), and material density (1.0 gcm−1) as each other and as the train set materials, but different YMRs (0.55, 1.05, or 2.00) (recall that the train set materials had YMR of 1.05). When the compared materials have the same YMR as each other, the predicted SMRs distinguish materials that have, on average, a 10% difference in true SMR regardless of whether or not the YMR matched that of the train set materials. However, when the compared materials have different YMRs, as large as a 15% difference in true SMRs is needed to distinguish TI materials by the predicted SMRs.
Panels (b-e) in Fig. 6 similarly show the minimum percent difference in true SMRs that is necessary to distinguish two compared materials by predicted SMRs when the compared materials have different or same transverse shear modulus (panel (b)), acoustic attenuation (panel (c)), sound speed (panel (d)), and material density (panel (e)). For all of these cases, the largest minimum percent difference in true SMRs needed to distinguish two materials by predicted SMRs was 20% (panel (b), μT of 2.0 versus 8.0 kPa).
Fig. 6, panel (f) depicts the minimum percent difference in true SMRs that is necessary to distinguish two compared materials by predicted SMRs when the compared materials have the same underlying material properties as each other and as the train set materials but the materials are interrogated by varying ARF PSFs sizes using the simulated matrix array. In these cases, the minimum percent difference in true SMR required to differentiate two materials using the predicted SMRs varied from 9% to 17%.
D. Ex Vivo and In Vivo Performance
Fig. 7(a) shows ARFI displacement profiles as median ± 0.5 × interquartile range (IQR) in ex vivo pig biceps femoris muscle when the lateral aspect of the transducer was oriented at 0° and 90° relative to muscle fibers. Similarly, panel (b) shows SWEI displacement profiles as median ± 0.5×IQR in the same muscle at 6 different lateral locations. The lateral location of the ARF excitation for SWEI was −3.4 mm. Induced displacement amplitude decreased with distance from the push location due to shear wave attenuation (predominantly caused by shear wave spreading). Panel (c) shows time-to-peak versus lateral distance as median ± 0.5×IQR at 0° and 90° for the calculation of the SWV. Note that the inverse of the slope indicates the SWV; therefore, the SWV was higher at 0° compared to 90°. Note, the SWV was calculated at each pixel with a sliding lateral window size of 2.5 mm to generate shear modulus images (Figs. 8 and 9).
Fig. 7.
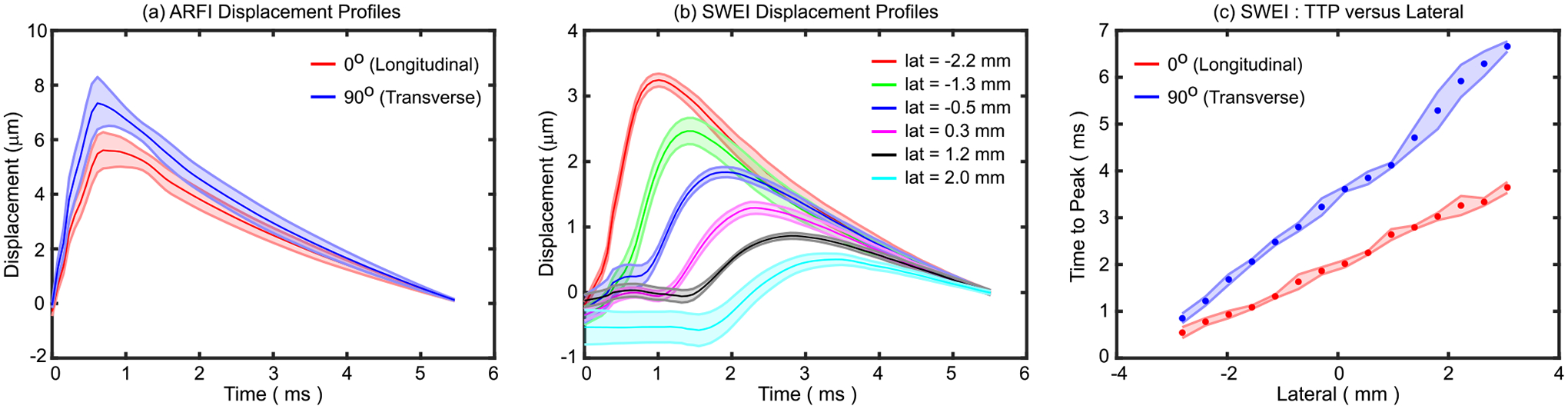
(a) ARFI displacement profiles in excised pig biceps femoris muscle when the lateral aspect of the transducer is oriented at 0° (red) and 90° with respect to muscle fibers. Data are plotted as median (solid line) ± 0.5×interquartile range (IQR, shaded region) over the 2D region of interest (ROI) shown in Fig. 8. (b) SWEI displacement profiles when the transducer is oriented at 0° with respect to muscle fibers. Data are plotted as median (solid line) ± 0.5×IQR (shaded region) in the same muscle over the axial range shown for the ROIs in Fig. 8 at 6 different lateral locations. The lateral location of the ARF excitation was −3.4 mm. (c) Time to peak (TTP) versus lateral distance when the transducer was oriented at 0° (red) and 90° (blue) with respect to muscle fibers for the calculation of the shear wave velocity. Data are plotted as median (circle marker) ± 0.5×IQR (shaded region) over the axial range shown for the ROI in Fig.8.
Fig. 8.
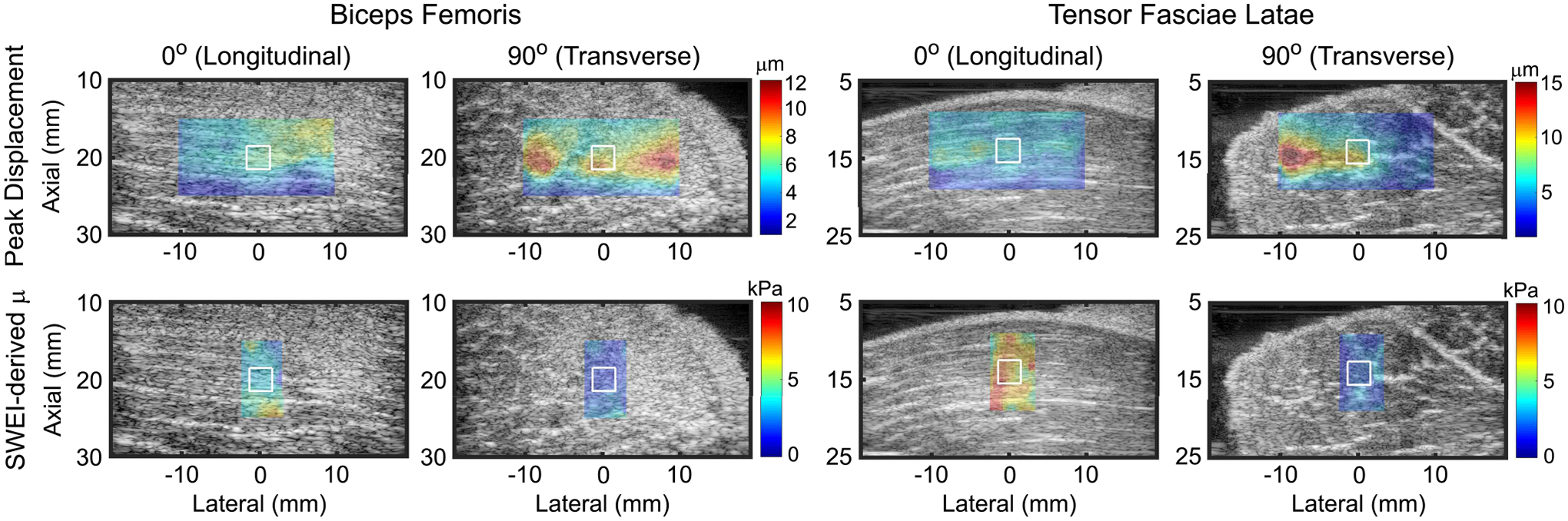
Parametric images depicting ARFI peak displacement (PD) (top row) and SWEI-derived shear elastic modulus (μ) (bottom row) in excised pig biceps femoris (first and second columns) and tensor fasciae latae (third and fourth columns) when the ARF PSF is aligned to interrogate predominantly the longitudinal (first and third columns) or transverse (second and fourth columns) shear elastic modulus. Peak displacement and shear modulus are overlaid with transparency on the matched B-modes for anatomical reference. White contours indicate measurement regions of interest. Note that PD and μ are inversely related and the color bar units and ranges differ between rows and columns.
Fig. 9.
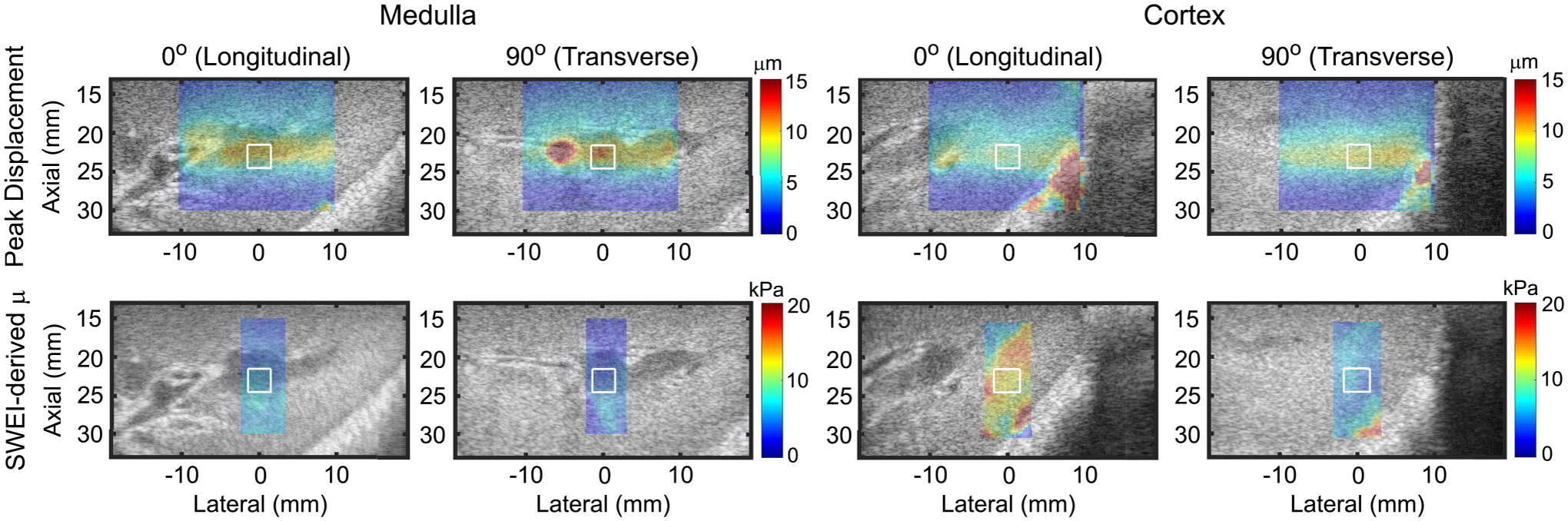
Parametric images depicting ARFI peak displacement (PD) (top row) and SWEI-derived shear elastic modulus (μ) (bottom row) in in vivo pig renal medulla (first and second columns) and cortex (third and fourth columns) when the ARF PSF is aligned to interrogate predominantly the longitudinal (first and third columns) or transverse (second and fourth columns) shear elastic modulus. Peak displacement and shear modulus are overlaid with transparency on the matched B-modes for anatomical reference. White contours indicate measurement regions of interest. Note that PD and μ are inversely related and the color bar units and ranges differ between rows and columns.
Representative images showing excised pig biceps femoris and tensor fasciae latae muscles are presented in Fig. 8, which depicts ARFI PD (top row) and SWEI-derived shear elastic modulus (μ) (bottom row). The data in the first and third columns (0°) were acquired with the linear array transducer positioned to interrogate primarily the longitudinal shear modulus (μL), e.g. the lateral transducer aspect was aligned along, and the long-axis of the ARF PSF was aligned across, the muscle fibers. The data in the second and fourth columns (90°) were acquired with the transducer positioned to interrogate primarily the transverse shear modulus (μT), e.g. the lateral transducer aspect was aligned across, and the long-axis of the ARF PSF was aligned along muscle fibers. The white contours indicate the ROIs used to calculate peak displacement ratios (PDT/PDL), from which SMRs were estimated using the empirical model, and SWEI-derived SMRs (μL/μT). In the biceps femoris, the SWEI-derived SMR was 2.15, and the ARFI-derived quantitative shear moduli ratio was 2.19, for a 1.9% absolute difference. In the tensor fasciae latae, the SWEI-derived SMR was 3.5, and the quantitative ARFI-derived SMR was 3.9, for an 11.4% absolute difference.
Figure 9 shows an example in vivo results in a pig kidney, with medulla and cortex visible. Parametric images of ARFI PD (top row) and SWEI-derived shear elastic modulus (μ) (bottom row) were acquired as in Fig. 8 but with alignment to nephron orientation. SWEI-derived SMRs were 1.26 and 2.3 in the medulla and cortex, respectively. After conversion by the empirical model, the corresponding ARFI PD-derived SMRs were 1.27 and 2.0. The absolute percent differences between ARFI- and SWEI-derived SMRs were 0.8% in the medulla and 13.0% in the cortex.
Fig. 10 shows linear regressions between ARFI PD- and SWEI-derived SMRs in ex vivo pig muscle (panel (a)) and in vivo pig kidney (panel (b)). In both cases, ARFI PD-derived SMRs were highly correlated with those derived by SWEI, with (R2, MAPE) values of (0.91, 13%) in ex vivo pig muscle and (0.99, 5.3%) in in vivo kidney.
Fig. 10.
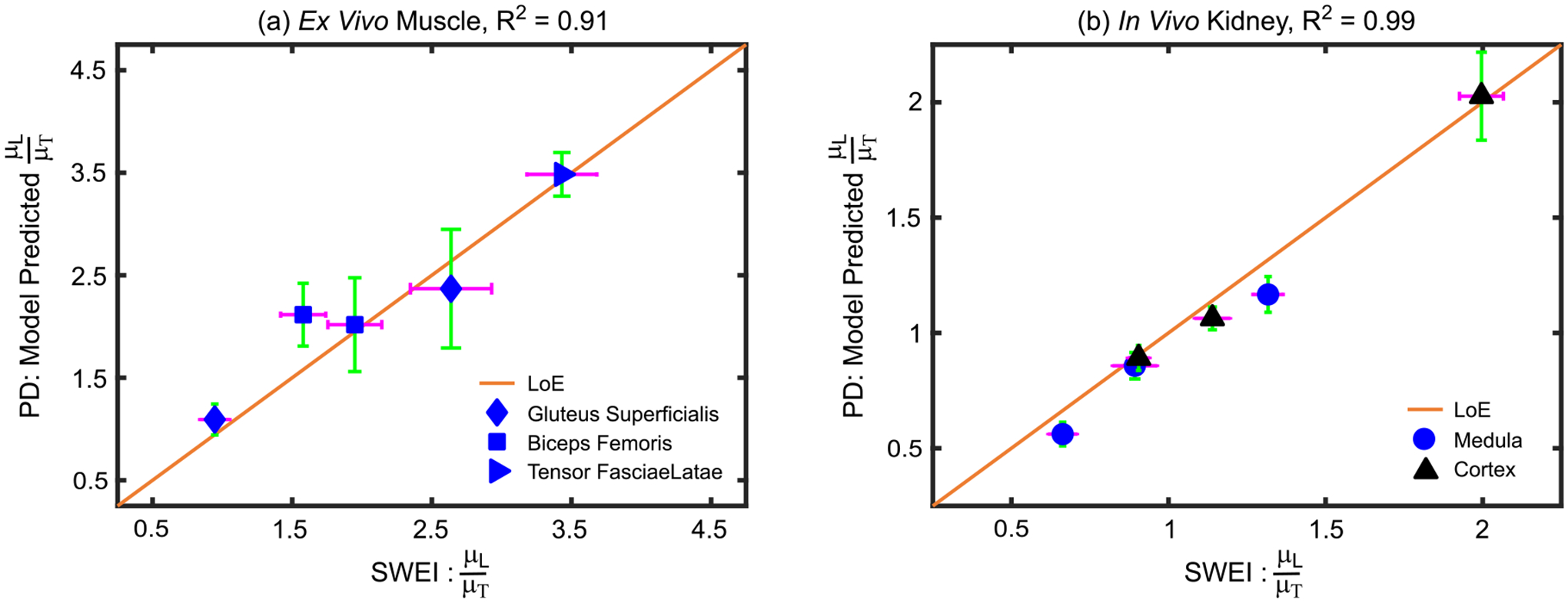
Quantitative ARFI- versus SWEI-derived shear moduli ratios in ex vivo pig skeletal muscle (a) and in vivo pig kidney (b), with the R2 value of the linear correlation included in the title. Data are plotted as median ± 0.5×IQR over the repeated acquisitions. IQR = interquartile range; LoE = line of equivalency.
IV. Discussion
This study evaluates the feasibility of converting the ratio of ARFI PDs, which are qualitative measures, to quantitative measures of the degree of shear elastic anisotropy via an empirically derived model. Fig. 1(a) shows that, with low error and high correlation, a third-order polynomial describes the relationship between PDRs and SMRs for the simulated TI train materials, which had SMRs of 0.15–6.65. SMRS in biological tissues typically range from 0.5 to 5.0 [9], [10], [14], [27]–[31], [36], but underlying pathologies may alter SMRs in tissue beyond this range. Thus, the simulated SMRs ranges of 0.15–6.65 for train set materials were chosen to develop an empirical model that was relevant to healthy as well as pathological tissue having very high longitudinal relative to transverse shear elastic modulus or vice versa. For this wide range of SMRs, a third-order polynomial described the relationship between PDR and SMR better than the previously implemented quadratic function [21], which was derived using only SMRs greater than one. Note that although the relevance of the empirical model to quantifying SMRs outside of 0.15–6.65 was not directly evaluated herein, it is likely that accurately measuring SMRs less than 0.15 or greater than 6.65 will require the development of a new empirical model using train set materials having the desired SMR range. Despite the broad range of evaluated shear moduli ratios, and the addition of 40 dB noise to the test set data, the derived model predicted the SMRs of the test materials with high accuracy. These data suggest that the 3rd order polynomial successfully relates observed ARFI PDR to true SMR when the imaging and material property conditions used to train and test the model were identical.
In Figs. 2–3, the effect of disparate training and test set material properties on the model performance is evaluated. In Fig. 2(a), despite large differences in YMR (−45% and 100%) between the train and test materials, the error in predicted SMRs remained low, and the predicted SMRs were generally not statistically different across YMRs. These results are consistent with previous research showing that ARFI PDRs primarily reflect SMRs with minimal influence from YMR [17]. This suggests that ARFI-derived SMRs are not corrupted by differences in underlying Young’s moduli ratios, which are generally unknown. Similarly, to Young’s modulus, Fig. 2(b) shows that, despite large differences in transverse shear modulus (−50% and 100%) between the train and test materials, the model predicted true SMR with low error. The predicted SMRs were not statistically different between materials with different transverse (and longitudinal) shear moduli. These results demonstrate that ARFI-derived SMR measures are not meaningfully influenced by the particular values of the underlying transverse or longitudinal shear moduli.
Low error in predicted SMRs was also observed in Fig. 3 when the acoustic attenuation (panel (a)) varied by −50% and 100% and sound speed (panel (b)) varied by −2.6% and 2.6% in test relative to train set materials. These results show that differences in the spatial distribution of ARF deposited in tissue due to different acoustic attenuations [24] do not meaningfully impact ARFI PD-derived SMR measurements. Further, ARFI-derived SMRs were shown to be robust to ARF excitation focusing errors due to differences in sound speed.
The results of Fig. 3 indicate that the empirical model’s estimates of SMR were not corrupted by variations in ARF size and spatial distribution, which cause differences in complex system inertia. Fig. 4 directly investigates the impact of complex system inertia on the empirical model’s prediction of SMR. In panel (a), predicted SMRs were accurate and not statistically different between materials with the same SMR but different densities. These data show that ARFI-derived SMR is relevant despite the variations in complex system inertia that could arise in tissues with different densities. The data in panel (b) further suggest model robustness to variations in complex system inertia; predicted SMRs were not statistically different between materials interrogated by different ARF PSFs sizes. Such narrowing and spreading of the ARF excitation beam could result from spatially uniform phase aberrations, suggesting that ARFI-derived SMR could be relevant in the presence of subdermal fat or other uniformly aberrating layers.
While encouraging, the results in Fig. 4(b) present a highly simplified view of the effects of phase aberration. Rather than uniform ARF beam spreading or narrowing, a more realistic result of phase aberration could be a change in the spatial asymmetry of the ARF excitation PSF, which could meaningfully impact the empirical model’s ability to accurately predict true SMRs. To understand why, consider that ARF PDRs are impacted by the shape of the ARFI excitation PSF. More specifically, the PSF asymmetry ratio, defined as the ratio of the PSF’s long- to short-axis length in the coronal plane, determines the degree to which the longitudinal or transverse shear modulus influences a given PD [19]. The smaller the asymmetry ratio, the more both moduli influence the outcome PD measure. Thus, as phase aberration distorts the ARF excitation PSF to become more spatially symmetric, the measured PD values reflect more of the combination of longitudinal and transverse moduli than that to which the derived empirical model is calibrated. Thus, the model may become less relevant to predicting the SMR from the observed PDRs. In Fig. 4(b), the asymmetry ratio of the ARF excitation PSFs that interrogated the train and test materials was maintained at 1.7 despite the overall increase or decrease in the PSF size. An in-depth analysis of the impact on the model performance of differences in the asymmetry ratios of the ARF excitations used to interrogate train and test set materials is a topic of ongoing investigation.
While Figs. 2–4 evaluate if predicted SMR differs between materials with the same SMR but different material and ARF excitation properties, Figs. 5–6 consider if materials with different true SMR can be distinguished by predicted SMR. The results in Fig. 5 show that, on average, two materials can be differentiated from each other by their predicted SMRs when their true SMRs differ by at least 10%, i.e. tissue features having at least a 10% difference in their true SMRs would be differentiated by ARFI predictions of such.
The data in Fig. 5 were generated using training and test set materials that had identical material properties (apart from their longitudinal shear moduli) and were interrogated using identical imaging parameters. Fig. 6 evaluates the impact of differences in material and ARF excitation properties on the ability to differentiate anisotropic materials by predicted SMRs. Panels (a and b) show that two materials with different Young’s moduli ratios or transverse shear modulus can be distinguished by their predicted SMR when their true SMR differs by, on average, at least 13.7% or 17.3%, respectively (average across off-diagonal values). These increases in the required difference in true SMRs needed to distinguish between materials with different (relative to same) Young’s moduli ratios and transverse shear moduli could be related to associated differences in jitter and displacement underestimation. For example, materials with higher transverse shear moduli will have lower displacement and, thus, less jitter caused by decorrelation. They will also have higher transverse shear wave speed for faster correction of displacement underestimation caused by shearing under the tracking PSF [25]. Such differences in displacement tracking could slightly alter the relationship between measured PDRs and true SMRs, making the derived empirical model less accurate. The associated error would make distinguishing materials by their predicted SMR more challenging.
In panel (c), the minimum average difference in true SMR needed to distinguish two materials by predicted SMRs increased from 11% to 14.3% when the compared materials had same versus different acoustic attenuations and, in panel (d), from 11.3% to 15.7% when the compared materials had same versus different sound speeds. These increases suggest that differences in the spatial distribution of acoustic radiation force in the media, with associated differences in the manifested complex system inertia, slightly alter the relationship between measured PDR and true SMR, making the derived empirical model less accurate. Interestingly, differences in material density, which also alter complex system inertia, did not increase the minimum difference in true SMR needed to distinguish materials. This is likely related to the low degree of density variation, which was simulated to be consistent with the expectation for soft tissue.
In panel (f), the minimum difference in true SMR needed to distinguish materials was lower when the compared materials were interrogated using different (12.3%, average of off-diagonal) versus same (15.3%, average of diagonal) ARF excitation focal configurations. At first review, this result seems counterintuitive. However, it is important to consider that the tracking focal configuration was fixed for all three ARFI excitation focal configurations. Because the size of the tracking PSF relative to the size of the ARF excitation PSF impacts signal decorrelation, jitter, and displacement underestimation, the interplay of the ARF excitation and tracking PSF focal configurations could impact empirical model performance [25]. A detailed evaluation of the tracking focal configuration’s impact is a topic of future investigation. Combining all panels in Fig. 6, the mean ± standard deviation of the minimum percent difference in SMR required by the model was 12.6 ± 2.8. Importantly, the minimum percent difference in true SMR required by the proposed method to distinguish two anisotropic tissues is below the range of expected variation with pathology in various tissues. For example, the mean percent difference of ultrasound shear wave-derived DoA between malignant and benign breast masses was approximately 221% [13], between healthy and hypertrophic myocardium was 79% [37]; and between young (0–4 years old) versus elderly (65–75 years old) skin was 300% [38]. Further, 52% difference in elastic DoA, and 40% difference in viscous DoA, derived by Viscoelastic Response (VisR) ultrasound [32], [39] was shown between boys with versus without Duchenne muscular dystrophy [14].
While the data in Fig. 6 suggest that the empirical models developed herein would sufficiently differentiate such changes in tissue due to diseases, other applications may require SMR resolution below 20% (worst empirical model SMR resolution, Fig. 6b). Future studies will investigate the feasibility of using machine learning models developed using training set materials with variable elastic and acoustic properties to improve the PDR-derived SMR resolution.
Figs. 7–10 show that experimental translation of ARFI-based SMR measurement in pig skeletal muscles ex vivo, and in pig kidney in vivo, yields results that are both physiologically expected (longitudinal greater than transverse shear elastic moduli) and consistent with SWEI-derived outcomes. While SWEI is an established method for assessing the shear modulus of tissue, the approach relies on the evaluation of shear wave propagation, with associated limitations [40], as described above. Although the imaging location was selected to minimize potential SWEI errors (i.e. by avoiding edges/structures that would cause shear wave reflections and focusing less than 25 mm in depth), we note that SWEI measures are considered as comparative benchmarks rather than ground truth validation for quantitative ARFI SMR measurements. However, the strong agreement between ARFI and SWEI outcomes suggests the feasibility of quantitative ARFI-derived SMR measurement ex vivo and in vivo.
Pig skeletal muscles and kidneys were chosen over elastically anisotropic tissue-mimicking phantoms [41]–[43] as media for experimentally translating ARFI SMR measurement for three primary reasons. First, relative to phantoms, muscle and kidney exhibit mechanical anisotropy that more closely resembles that which naturally exists in anisotropic organs. More specifically, published methods generate phantoms that are transversely isotropic, but in actuality, the mechanical anisotropy of tissue is more complex. Further, published methods produce phantoms that have low viscosity, but tissue is viscoelastic. These are meaningful differences because, considering that the empirical model was derived from simulated transversely isotropic, elastic materials, its performance in viscoelastic tissues that are not ideally transversely isotropic should be demonstrated. Second, muscle and kidney contain more structures and heterogeneities than custom-made mechanically anisotropic phantoms. Structures and heterogeneities cause wave reflections and other distortions that could impact experimental measurements. Thus, demonstrating ARFI SMR measurement in muscle and kidney more closely recapitulates the challenges of clinical application and better demonstrates the developed approach’s robustness to such challenges than possible using phantoms. Third, calibrated mechanically anisotropic phantoms are not commercially available, and methods for custom making mechanically anisotropic phantoms are not standardized. Following a specific recipe or process does not yield phantoms with known elasticities or viscosities, let alone degrees of anisotropy. As a result, alternative methods must be employed for calibrating the custom-made phantoms, just as was necessary for muscle and kidney, diminishing the utility of phantom investigations.
While both simulation and experimental results suggest that a 3rd order polynomial describes the relationship between PDR and SMR, the model was derived empirically with no physical basis for its selection. We opted for an empirical approach because, in the context of the complex 3-D system inertia that impacts ARFI PD, an analytic solution is not straightforward. However, a physically-based analytical expression describing the relationship between PDR and SMR would avoid time-consuming simulations and make the approach more broadly generalizable. Prior work describes the analytical equation of shear wave propagation in transversely isotropic materials assuming plane wave propagation [4], [44], [45]. Other work by Wang et al. develops a closed-form solution of displacement in the transversely isotropic half-space subject to three-dimensional loading [46], and Liao et al. developed a closed solution for displacement and stress due to three-dimensional point loads [47]. Future work will build upon these contributions to investigate the feasibility of deriving a closed-form relationship between PDR and SMR.
The translation of quantitative ARFI-derived SMR measurement into routine clinical practice will be faced with challenges. First, a unique model relating qualitative PDRs to quantitative SMRs must be empirically derived for each set of imaging parameters. Creating a bank of preformed models for a wide collection of focal depths, focal configurations, center frequencies, and other imaging parameters would be necessary. Alternatively, more generalizable models may be possible, including those that are derived using machine learning approaches. Second, while the herein described in silico performance analyses considered tissue attenuation, sound speed, and density to be isotropic and homogeneous, such assumptions may not hold in vivo. Further investigation is needed to determine the potential impacts of anisotropic attenuation, sound speed, and tissue density. Similarly, future work will evaluate performance in heterogeneous media, including those in which heterogeneities impact the spatial asymmetry of the ARF PSF. Some degree of ARF PSF distortion due to phase aberration was likely present for the biceps femoris and tensor fasciae latae muscles, which were imaged ex vivo as part of a whole leg with overlying skin and transcutaneous fat intact. Notably, the kidney, which was exteriorized for in vivo imaging, did not have an overlying aberration layer, which could explain the higher R2 value of the linear regression for kidney (R2 = 0.99) versus muscle (R2 = 0.91). A systematic study of the impact of phase aberration on ARF-derived SMR measurement will be pursued in future work.
There were several limitations to the study design. First, the accuracy and robustness of predicted SMRs, and their ability to distinguish between materials with different true SMRs, were systematically evaluated for only one ARF excitation focal depth. While consistent performance is expected for a wide range of focal depths, the impact of focal depth on empirical model performance will be studied in future work. Second, the simulated TI materials, muscle, and kidney evaluated in this work were assumed to be purely elastic materials. However, PD is impacted by tissue viscosity [39], [48]. The influence of tissue viscosity on quantitative ARFI-derived SMR measurement was neglected herein but will be investigated in future work. Third, all of the simulated materials were homogeneous, i.e. they contained no inclusions, layers, or other features. While experiments performed in pig skeletal muscles suggest that the method may be robust to heterogeneities such as tissue layers, more work is needed to fully evaluate performance in heterogeneous media. Fourth, DoA was assessed as a point measure in this work. A 2-D image of DoA can be generated by mechanically translating a linear array transducer or electronic translation of the aperture of a matrix array [20]. Future work will implement aperture translation for 2D DoA image generation. Finally, the described advantages to measuring SMR by observing displacements in only the ARF region of excitation, without observing shear wave propagation, remain to be shown. Systematically comparing ARFI to shear wave-based measurement methods in heterogeneous media and with deep focal depths is a topic of an on-going investigation.
V. Conclusion
This work demonstrates an ARFI-based method for quantifying mechanical DoA, expressed as the ratio of longitudinal to transverse shear elastic moduli, in tissue. In this approach, qualitative ratios of ARFI-induced PDs achieved with the long-axis of a spatially asymmetric ARF PSF aligned along versus across the material AoS are converted to SMRs using models empirically derived from simulations of known elastic anisotropy. In silico analyses suggest that empirical models convert qualitative ARFI PDRs to SMRs with high accuracy (RMSE = 0.06 and MAPE = 1.75%). The quantitative ARFI-derived DoA outcomes distinguished TI materials with at least 12.6 ± 2.8 percent difference in true SMR, with the better performance achieved when the compared materials have consistent material properties. ARFI-derived SMR in pig skeletal muscles, ex vivo, and kidney, in vivo were corroborated by SWEI, demonstrating the relevance of the ARFI approach to assessing mechanical DoA in biological tissue and suggesting the method’s potential clinical feasibility. An important advantage to ARFI-derived quantitative DoA measurement is that the method interrogates displacement in the ARF region of excitation only and does not require observation of shear wave propagation. Overall, this work demonstrates a new, ARFI-based method for quantifying mechanical DoA in biological tissues that shows promise for future clinical application.
Acknowledgment
The authors thank the physicians and staff in the Francis Owen Blood Research Lab at the University of North Carolina at Chapel Hill for providing the excised pig muscles and help in the in vivo experiment and Siemens Healthineers, Ultrasound Division, Issaquah, WA, USA.
This work was supported by NIH under Grant R01DK107740, 2R01HL092944, and 1R01NS074057
References
- [1].Fung Y-C, Mechanical Properties of Living Tissues, 2nd ed. New York, NY: Springer New York, 1993. [Google Scholar]
- [2].Sigrist RMS, Liau J, El Kaffas A, Chammas MC, and Willmann JK, “Ultrasound Elastography: Review of Techniques and Clinical Applications,” Theranostics, vol. 7, no. 5, pp. 1303–1329, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Venkatesh SK and Ehman RL, Magnetic Resonance Elastography, vol. 9781493915. New York, NY: Springer New York, 2014. [Google Scholar]
- [4].Rouze NC, Wang MH, Palmeri ML, and Nightingale KR, “Finite element modeling of impulsive excitation and shear wave propagation in an incompressible, transversely isotropic medium.,” J. Biomech, vol. 46, no. 16, pp. 2761–8, Nov. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Gennisson J-LL, Deffieux T, Macé E, Montaldo G, Fink M, and Tanter M, “Viscoelastic and anisotropic mechanical properties of in vivo muscle tissue assessed by supersonic shear imaging.,” Ultrasound Med. Biol, vol. 36, no. 5, pp. 789–801, May 2010. [DOI] [PubMed] [Google Scholar]
- [6].Yeh C, Sheu Y, Kuo P, and Li P, “Investigation on anisotropy of elastic properties in tendon using shear wave elasticity imaging,” 2012 IEEE Int. Ultrason. Symp., pp. 1359–1362, Oct. 2012. [Google Scholar]
- [7].Hossain MM et al. , “Mechanical Anisotropy Assessment in Kidney Cortex Using ARFI Peak Displacement: Preclinical Validation and Pilot In Vivo Clinical Results in Kidney Allografts.,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 66, no. 3, pp. 551–562, Mar. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Sinkus R et al. , “Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography.,” Magn. Reson. Med, vol. 53, no. 2, pp. 372–87, Feb. 2005. [DOI] [PubMed] [Google Scholar]
- [9].Gennisson J-LL, Grenier N, Combe C, and Tanter M, “Supersonic Shear Wave Elastography of In Vivo Pig Kidney: Influence of Blood Pressure, Urinary Pressure and Tissue Anisotropy,” Ultrasound Med. Biol, vol. 38, no. 9, pp. 1559–1567, Sep. 2012. [DOI] [PubMed] [Google Scholar]
- [10].Leong SS et al. , “Stiffness and Anisotropy Effect on Shear Wave Elastography: A Phantom and in Vivo Renal Study,” Ultrasound Med. Biol, vol. 00, no. 00, pp. 1–12, Oct. 2019. [DOI] [PubMed] [Google Scholar]
- [11].Ruby L et al. , “Which Confounders Have the Largest Impact in Shear Wave Elastography of Muscle and How Can They be Minimized? An Elasticity Phantom, Ex Vivo Porcine Muscle and Volunteer Study Using a Commercially Available System,” Ultrasound Med. Biol, vol. 00, no. 00, Jul. 2019. [DOI] [PubMed] [Google Scholar]
- [12].Skerl K, Vinnicombe S, Thomson K, McLean D, Giannotti E, and Evans A, “Anisotropy of Solid Breast Lesions in 2D Shear Wave Elastography is an Indicator of Malignancy,” Acad. Radiol, vol. 23, no. 1, pp. 53–61, Jan. 2016. [DOI] [PubMed] [Google Scholar]
- [13].Chen YL, Gao Y, Chang C, Wang F, Zeng W, and Chen JJ, “Ultrasound shear wave elastography of breast lesions: Correlation of anisotropy with clinical and histopathological findings,” Cancer Imaging, vol. 18, no. 1, pp. 1–11, Dec. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Moore CJ et al. , “In Vivo Viscoelastic Response (VisR) Ultrasound for Characterizing Mechanical Anisotropy in Lower-Limb Skeletal Muscles of Boys with and without Duchenne Muscular Dystrophy,” Ultrasound Med. Biol, vol. 44, no. 12, pp. 2519–2530, Aug. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Hossain M et al. , “Viscoelastic Response Ultrasound Detects Increased Degree of Mechanical Anisotropy with Ischemia-Reperfusion Injury in Pig Kidney, In Vivo,” in 2018 IEEE International Ultrasonics Symposium (IUS), 2018, pp. 1–4. [Google Scholar]
- [16].Hossain MM et al. , “Viscoelastic Response Ultrasound Detects Changes in Degree of Mechanical Anisotropy with Renal Fibrosis in Pig Model,” in 2019 IEEE International Ultrasonics Symposium (IUS), 2019, vol. 2019-Octob, pp. 415–418. [Google Scholar]
- [17].Hossain MM et al. , “In vivo mechanical anisotropy assessment in renal cortex using ARFI peak displacement,” in 2017 IEEE International Ultrasonics Symposium (IUS), 2017, vol. 64, no. 6, pp. 1–4. [Google Scholar]
- [18].Hossain MM and Gallippi CM, “Estimation of degree of anisotropy in transversely isotropic (TI) elastic materials from Acoustic Radiation Force (ARF)-induced peak displacements,” in 2015 IEEE International Ultrasonics Symposium (IUS), 2015, pp. 1–4. [Google Scholar]
- [19].Hossain M, Moore CJ, and Gallippi CM, “Acoustic Radiation Force Impulse-Induced Peak Displacements Reflect Degree of Anisotropy in Transversely Isotropic Elastic Materials,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 64, no. 6, pp. 989–1001, Jun. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Moore CJ, Hossain MDM, and Gallippi CM, “2D ARFI and Viscoelastic Response (VisR) anisotropy imaging in skeletal muscle,” in 2017 IEEE International Ultrasonics Symposium (IUS), 2017, pp. 1–4. [Google Scholar]
- [21].Hossain M and Gallippi CM, “On the feasibility of quantifying mechanical anisotropy in transversely isotropic elastic materials using acoustic radiation force (ARF)-induced displacements,” in Medical Imaging 2019: Ultrasonic Imaging and Tomography, 2019, no. March, p. 12. [Google Scholar]
- [22].Jensen JA, Lyngby D, Medical P, Engineering B, and Technology I, “Field: A Program for Simulating Ultrasound Systems,” in 10th Nordic-Baltic Conference on Biomedical Imaging, 1996, vol. 34, pp. 351–353. [Google Scholar]
- [23].Jensen JA and Svendsen NB, “Calculation of pressure fields from arbitrarily shaped, apodized, and excited ultrasound transducers.,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 39, no. 2, pp. 262–7, Jan. 1992. [DOI] [PubMed] [Google Scholar]
- [24].Palmeri ML, Sharma AC, Bouchard RR, Nightingale RW, and Nightingale KR, “A finite-element method model of soft tissue response to impulsive acoustic radiation force.,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 52, no. 10, pp. 1699–712, Oct. 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Palmeri ML, McAleavey S. a., Trahey GE, and Nightingale KR, “Ultrasonic tracking of acoustic radiation force-induced displacements in homogeneous media,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 53, no. 7, pp. 1300–1313, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Pinton GF, Dahl JJ, and Trahey GE, “Rapid tracking of small displacements with ultrasound.,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 53, no. 6, pp. 1103–17, Jun. 2006. [DOI] [PubMed] [Google Scholar]
- [27].Wang M, Byram B, Palmeri M, Rouze N, and Nightingale K, “Monitoring Acoustic Radiation Force Induced Shear Waves Using a 2-D Matrix Ultrasound Array,” vol. 32, no. 9, pp. 1671–1684, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Chaudhry H, Bukiet B, and Findley T, “Mathematical Analysis of Applied loads on skeletal muscles During Manual Therapy,” J. Am. Osteopath. Assoc, vol. 108, no. 12, pp. 680–8, Dec. 2008. [PubMed] [Google Scholar]
- [29].Deffieux T, Montaldo G, Tanter M, and Fink M, “Shear wave spectroscopy for in vivo quantification of human soft tissues visco-elasticity,” IEEE Trans. Med. Imaging, vol. 28, no. 3, pp. 313–322, 2009. [DOI] [PubMed] [Google Scholar]
- [30].Urban MW, Chen S, and Fatemi M, “A Review of Shearwave Dispersion Ultrasound Vibrometry (SDUV) and its Applications,” Curr. Med. Imaging Rev, vol. 8, no. 1, pp. 27–36, Feb. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Lee W-NN et al. , “Mapping myocardial fiber orientation using echocardiography-based shear wave imaging,” IEEE Trans. Med. Imaging, vol. 31, no. 3, pp. 554–562, Mar. 2012. [DOI] [PubMed] [Google Scholar]
- [32].Selzo MR, Moore CJ, Hossain MM, Palmeri ML, and Gallippi CM, “On the Quantitative Potential of Viscoelastic Response (VisR) Ultrasound Using the One-Dimensional Mass-Spring-Damper Model.,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 63, no. 9, pp. 1276–87, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Nightingale K, McAleavey S, and Trahey G, “Shear-wave generation using acoustic radiation force: in vivo and ex vivo results.,” Ultrasound Med. Biol, vol. 29, no. 12, pp. 1715–1723, Dec. 2003. [DOI] [PubMed] [Google Scholar]
- [34].Hossain MM and Gallippi CM, “Electronic Point Spread Function Rotation Using a Three-Row Transducer for ARFI-Based Elastic Anisotropy Assessment: In Silico and Experimental Demonstration.,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 68, no. 3, pp. 632–646, Mar. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Deffieux T, Gennisson JL, Bercoff J, and Tanter M, “On the effects of reflected waves in transient shear wave elastography,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 58, no. 10, pp. 2032–2035, 2011. [DOI] [PubMed] [Google Scholar]
- [36].Qin EC, Jugé L, Lambert SA, Paradis V, Sinkus R, and Bilston LE, “In vivo anisotropic mechanical properties of dystrophic skeletal muscles measured by anisotropic MR elastographic imaging: the mdx mouse model of muscular dystrophy.,” Radiology, vol. 273, no. 3, pp. 726–35, Dec. 2014. [DOI] [PubMed] [Google Scholar]
- [37].Villemain O et al. , “Myocardial Stiffness Evaluation Using Noninvasive Shear Wave Imaging in Healthy and Hypertrophic Cardiomyopathic Adults,” JACC Cardiovasc. Imaging, vol. 12, no. 7, pp. 1135–1145, Jul. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Ruvolo EC Jr., Stamatas GN, and Kollias N, “Skin Viscoelasticity Displays Site- and Age-Dependent Angular Anisotropy,” Skin Pharmacol. Physiol, vol. 20, no. 6, pp. 313–321, 2007. [DOI] [PubMed] [Google Scholar]
- [39].Hossain MM and Gallippi CM, “Viscoelastic Response Ultrasound Derived Relative Elasticity and Relative Viscosity Reflect True Elasticity and Viscosity: In Silico and Experimental Demonstration.,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 67, no. 6, pp. 1102–1117, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Deng Y, Rouze NC, Palmeri ML, and Nightingale KR, “On System-Dependent Sources of Uncertainty and Bias in Ultrasonic Quantitative Shear-Wave Imaging.,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 63, no. 3, pp. 381–93, Mar. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Chatelin S et al. , “Anisotropic polyvinyl alcohol hydrogel phantom for shear wave elastography in fibrous biological soft tissue: a multimodality characterization,” Phys. Med. Biol, vol. 59, no. 22, pp. 6923–6940, Nov. 2014. [DOI] [PubMed] [Google Scholar]
- [42].Urban MW et al. , “Characterization of transverse isotropy in compressed tissue-mimicking phantoms,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 62, no. 6, pp. 1036–1046, Jun. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Caenen A, Knight AE, Rouze NC, Bottenus NB, Segers P, and Nightingale KR, “Analysis of multiple shear wave modes in a nonlinear soft solid: Experiments and finite element simulations with a tilted acoustic radiation force,” J. Mech. Behav. Biomed. Mater, vol. 107, no. January, p. 103754, Jul. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Qiang B, Brigham JC, McGough RJ, Greenleaf JF, and Urban MW, “Mapped Chebyshev pseudo-spectral method for simulating the shear wave propagation in the plane of symmetry of a transversely isotropic viscoelastic medium,” Med. Biol. Eng. Comput, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Carcione JM, Kosloff D, and Kosloff R, “Wave-propagation simulation in an elastic anisotropic (transversely isotropic) solid,” Q. J. Mech. Appl. Math, vol. 41, no. 3, pp. 319–346, 1988. [Google Scholar]
- [46].Der Wang C and Liao JJ, “Elastic solutions for stresses in a transversely isotropic half-space subjected to three-dimensional buried parabolic rectangular loads,” Int. J. Numer. Anal. Methods Geomech, vol. 26, no. 14, pp. 1449–1476, 2002. [Google Scholar]
- [47].Liao J, Hu T, and Wang C, “Elastic solutions for an inclined transversely isotropic material due to three-dimensional point loads,” J. Mech. Mater. Struct, vol. 3, no. 8, pp. 1521–1547, Oct. 2008. [Google Scholar]
- [48].Hossain MM, Nichols T, Merricks E, and Gallippi C, “Viscoelastic response (VisR)-derived relative elasticity and relative viscosity reflect tissue elasticity and viscosity: In silico and experimental demonstration in liver,” in 2017 IEEE International Ultrasonics Symposium (IUS), 2017, no. 2, pp. 1–1. [Google Scholar]


