Skip to main content
SpringerLink
Log in

On Estimation Errors in Optical Communication and Location

  • SURVEY ARTICLES
  • Published:
Automation and Remote Control Aims and scope Submit manuscript

Abstract

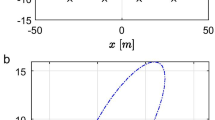
We consider several problems of parameter estimation based on observations of inhomogeneous Poisson processes arising in various practical applications of optical communication and location. The intensity function of the observed process consists of a periodic signal depending on an unknown parameter and a constant noise intensity. The asymptotic behavior of maximum likelihood and Bayesian estimators in cases of phase and frequency modulation of signals is described. Particular attention is paid to signals of various regularity (smooth, continuous but nondifferentiable, and of change-point type). Numerical simulations illustrate the results presented. This paper is a survey of results on the behavior of estimators in cases of frequency and phase modulation of signals of various regularity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.
Fig. 11.
Fig. 12.
Fig. 13.

Similar content being viewed by others

REFERENCES

  1. Vishnevskii, V.M. and Dudin, A.N., Queueing systems with correlated arrival flows and their applications to modeling telecommunication networks, Autom. Remote Control, 2017, vol. 78, no. 8, pp. 1361–1403.

    Article  MathSciNet  MATH  Google Scholar 

  2. Nazarov, A.A. and Lyubina, T.V., The non-Markov dynamic RQ system with the incoming MMP flow of requests, Autom. Remote Control, 2013, vol. 74, no. 7, pp. 1132–1143.

    Article  MathSciNet  MATH  Google Scholar 

  3. Proskurnikov, A.V. and Fradkov, A.L., Problems and methods of network control, Autom. Remote Control, 2016, vol. 77, no. 10, pp. 1711–1740.

    Article  MathSciNet  MATH  Google Scholar 

  4. Rao, M.M., Optical Communication, Hyderabad: Universities Press, 2001.

    Google Scholar 

  5. Fundamental Astronomy, Karttunen, H., Kröger P., Oja, H., Poutanene, M., and Donner, K.J., Eds., New York: Springer, 2017.

  6. Chen, V.C., The Micro-Doppler Effect in Radar. 2nd ed., Boston: Artech House, 2019.

    Google Scholar 

  7. Breyer, B., Physical principles of the Doppler effect and its application in medicine, in Color Doppler, 3D and 4D Ultrasound in Gynecology, Infertility and Obstetrics, Kupesic, S., Ed., Jaypee Brothers Medical Publ., 2011, pp. 1–11.

  8. Handbook of Position Location: Theory, Practice and Advances. 2nd ed., Zekavat, S.A.R. and Buehrer, R.M., Eds., Hoboken: John Wiley and Sons, 2019.

  9. Chernoyarov, O.V. and Kutoyants, Yu.A., Poisson source localization on the plane. Smooth case, Metrika, 2020, vol. 83, no. 4, pp. 411–435.

    Article  MathSciNet  MATH  Google Scholar 

  10. Chernoyarov, O.V., Dachian, S., and Kutoyants, Yu.A., Poisson source localization on the plane. Cusp case, Ann. Inst. Stat. Math., 2020, vol. 72, no. 5, pp. 1137–1157.

    Article  MathSciNet  MATH  Google Scholar 

  11. Bandyopdhyay, M.N., Optical Communication and Networks, Prentice Hall of India Private, 2014.

  12. Bar-David, I., Communication under the Poisson regime, IEEE Trans. Inf. Theory, 1969, vol. IT–15, no. 1, pp. 31–37.

    Article  MathSciNet  MATH  Google Scholar 

  13. Wyner, A.D., Capacity and error exponent for the direct detection photon channel—Parts I and II, IEEE Trans. Inf. Theory, 1988, vol. IT–34, pp. 1449–1471.

    Article  MATH  Google Scholar 

  14. Liptser, R.Sh. and Shiryaev, A.N., Statistika sluchainykh protsessov, Moscow: Nauka, 1974. Translated under the title: Statistics of Random Processes, Berlin: Springer, 2001.

    Google Scholar 

  15. Ibragimov, I.A. and Khasminskii, R.Z., Estimation of a signal parameter in Gaussian white noise, Probl. Inf. Transm., 1974, vol. 10, no. 1, pp. 31–46.

    Google Scholar 

  16. Kutoyants, Yu.A., Parameter Estimation for Stochastic Processes, Berlin: Heldermann, 1984.

    MATH  Google Scholar 

  17. Ibragimov, I.A. and Khas’minskii, R.Z., Asimptoticheskaya teoriya otsenivaniya, Moscow: Nauka, 1979. Translated under the title: Statistical Estimation. Asymptotic Theory, New York: Springer, 1981.

    MATH  Google Scholar 

  18. Prakasa Rao, B.L.S., Estimation of the location of the cusp of a continuous density, Ann. Math. Stat., 1968, vol. 39, no. 1, pp. 76–87.

    Article  MathSciNet  MATH  Google Scholar 

  19. Dachian, S., Estimation of the location of a \(0 \)-type or \(\infty \)-type singularity by Poisson observations, Stat.: J. Theor. Appl. Stat., 2011, vol. 45, no. 5, pp. 509–523.

    Article  MathSciNet  MATH  Google Scholar 

  20. Hajek, J., Local asymptotic minimax and admissibility in estimation, Proc. Sixth Berkeley Symp. Math. Stat. Probab., 1972, vol. 1, pp. 175–194.

    MathSciNet  MATH  Google Scholar 

  21. Kutoyants, Yu.A., Statistical Inference for Spatial Poisson Processes, New York: Springer, 1998.

    Book  MATH  Google Scholar 

  22. Kutoyants, Yu.A., Parameter estimation of intensity of inhomogeneous Poisson processes, Probl. Control Inf. Theory, 1979, vol. 8, pp. 137–149.

    MATH  Google Scholar 

  23. Kutoyants, Yu.A., Multidimensional parameter estimation of intensity of inhomogeneous Poisson processes, Probl. Control Inf. Theory, 1982, vol. 11, pp. 325–334.

    MathSciNet  MATH  Google Scholar 

  24. Prakasa Rao, B.L.S., Asymptotic theory of least squares estimator in a nonregular nonlinear regression model, Stat. Probab. Lett., 1985, vol. 3, no. 1, pp. 15–18.

    Article  MathSciNet  MATH  Google Scholar 

  25. Prakasa Rao, B.L.S., Estimation of cusp in nonregular nonlinear regression models, J. Multivariate Anal., 2004, vol. 88, no. 2, pp. 243–251.

    Article  MathSciNet  MATH  Google Scholar 

  26. Doring, M., Asymmetric cusp estimation in regression models, Stat.: J. Theor. Appl. Stat., 2015, vol. 49, no. 6, pp. 1279–1297.

    Article  MathSciNet  MATH  Google Scholar 

  27. Doring, M. and Jensen, U., Smooth change point estimation in regression models with random design, Ann. Inst. Stat. Math., 2015, vol. 67, pp. 595–619.

    Article  MathSciNet  MATH  Google Scholar 

  28. Raimondo, M., Minimax estimation of sharp change points, Ann. Stat., 1998, vol. 26, no. 4, pp. 1379–1397.

    Article  MathSciNet  MATH  Google Scholar 

  29. Dachian, S., Estimation of cusp location by Poisson observations, Stat. Inference Stochastic. Process., 2003, vol. 6, no. 1, pp. 1–14.

    Article  MathSciNet  MATH  Google Scholar 

  30. Dachian, S. and Kutoyants, Yu.A., On cusp estimation of ergodic diffusion process, J. Stat. Plann. Inference, 2003, vol. 117, pp. 153–166.

    Article  MathSciNet  MATH  Google Scholar 

  31. Fujii, T., An extension of cusp estimation problem in ergodic diffusion processes, Stat. Probab. Lett., 2010, vol. 80, no. 9–10, pp. 779–783.

    Article  MathSciNet  MATH  Google Scholar 

  32. Kutoyants, Yu.A., On cusp location estimation for perturbed dynamical systems, Scand. J. Stat., 2019, vol. 46, pp. 1206–1226.

    Article  MathSciNet  MATH  Google Scholar 

  33. Chernoyarov, O.V., Dachian, S., and Kutoyants, Yu.A., On parameter estimation for cusp-type signals, Ann. Inst. Stat. Math., 2018, vol. 70, no. 1, pp. 39–62.

    Article  MathSciNet  MATH  Google Scholar 

  34. Kutoyants, Yu.A., On localization of source by hidden Gaussian processes with small noise, Ann. Inst. Stat. Math., 2021, vol. 73, no. 4, pp. 671–702.

    Article  MathSciNet  MATH  Google Scholar 

  35. Pflug, G.C., A statistically important Gaussian process, Stochastic Process. Appl., 1982, vol. 13, pp. 45–47.

    Article  MathSciNet  MATH  Google Scholar 

  36. Novikov, A.A., Kordzakhia, N.E., and Ling, T., On moments of Pitman estimators: the case of fractional Brownian motion, Theory Probab. Appl., 2014, vol. 58, no. 4, pp. 601–614.

    Article  MathSciNet  MATH  Google Scholar 

  37. Dachian, S., Kordzakhia, N., Kutoyants, Yu.A., and Novikov, A., Estimation of cusp location of stochastic processes: a survey, Stat. Inference Stochastic Process., 2018, vol. 21, no. 2, pp. 345–362.

    Article  MathSciNet  MATH  Google Scholar 

  38. Pyke, R., The supremum and infimum of the Poisson process, Ann. Math. Stat., 1959, vol. 30, pp. 568–576.

    Article  MathSciNet  MATH  Google Scholar 

  39. Skorokhod, A.V., Sluchainye protsessy s nezavisimymi prirashcheniyami, Moscow: Nauka, 1964. Translated under the title: Random Processes with Independent Increments, Dordrecht: Kluwer, 1991.

    Google Scholar 

  40. Shorack, G.R. and Wellner, J.A., Empirical Processes with Applications to Statistics, New York: John Wiley and Sons, 1986.

    MATH  Google Scholar 

  41. Pflug, G.C., On an Argmax-distribution connected to the Poisson process, in Proc. Fifth Prague Conf. Asymptotic Stat., Mandl, P. and Huskova, M., Eds., 1993. P. 123–130.

  42. Mosyagin, V.E. and Shvemler, N.A., Distribution of the time of attaining the maximum for the difference of the two Poisson processes with negative linear drift, Sib. Elektron. Mat. Izv., 2016, vol. 13, pp. 1229–1248.

    MATH  Google Scholar 

  43. Mosyagin, V.E. and Shvemler, N.A., Local properties of the limiting distribution of the statistical estimator for jump point of a density, Sib. Elektron. Mat. Izv., 2017, vol. 14, pp. 1307–1316.

    MathSciNet  MATH  Google Scholar 

  44. Mosyagin, V.E., Asymptotics for the distribution of the time of attaining the maximum for a trajectory of a Poisson process with drift and break, Theory Probab. Appl., 2021, vol. 66, no. 1, pp. 75–88.

    Article  MathSciNet  MATH  Google Scholar 

  45. Dachian, S., On limit likelihood ratio processes of some change-point type statistical models, J. Stat. Plann. Inference, 2010, vol. 140, pp. 2682–2692.

    Article  MathSciNet  MATH  Google Scholar 

  46. Ibragimov, I.A. and Khasminskii, R.Z., Parameter estimation for a discontinuous signal in white Gaussian noise, Probl. Inf. Transm., 1975, vol. 11, no. 3, pp. 203–212.

    Google Scholar 

  47. Galun, S.A. and Trifonov, A.P., Detection and estimation of the time when the Poisson flow intensity changes, Autom. Remote Control, 1982, vol. 43, no. 6, pp. 782–790.

    MATH  Google Scholar 

  48. Golubev, G.K., Fisher’s method of scoring in the problem of frequency estimation, J. Sov. Math., 1984, vol. 25, no. 3, pp. 1125–1139.

    Article  MATH  Google Scholar 

  49. Helstrom, C., Estimation of modulation frequency of a light beam, Optical Space Communication. Proc. MIT-NASA Workshop Held at Williams College, Kennedy, R.S. and Karp, S., Eds., (Williamstown, MA, August 4–17, 1968) Appendix E, 1968.

  50. Vere-Jones, D., On the estimation of frequency in point-process data, J. Appl. Probab., 1982, vol. 19(A), pp. 383–394.

    Article  MathSciNet  MATH  Google Scholar 

  51. Hall, P., Reimann, J., and Rice, J., Nonparametric estimation of a periodic function, Biometrika, 2000, vol. 87, no. 3, pp. 545–557.

    Article  MathSciNet  MATH  Google Scholar 

  52. Hopfner, R. and Kutoyants, Yu.A., On frequency estimation for a periodic ergodic diffusion process, Probl. Inf. Transm., 2012, vol. 48, no. 2, pp. 127–141.

    Article  MathSciNet  MATH  Google Scholar 

  53. Burnashev, M.V. and Kutoyants, Yu.A., On the sphere-packing bound, capacity, and similar results for Poisson channels, Probl. Inf. Transm., 1999, vol. 35, no. 2, pp. 95–111.

    MathSciNet  MATH  Google Scholar 

  54. Burnashev, M.V. and Kutoyants, Yu.A., On minimal \(\alpha \)-mean error parameter transmission over Poisson channel, IEEE Trans. Inf. Theory, 2001, vol. IT–47, no. 6, pp. 2505–2515.

    Article  MathSciNet  MATH  Google Scholar 

  55. Kabanov, Yu.M., The capacity of a Poisson type channel, Theory Probab. Appl., 1978, vol. 23, no. 1, pp. 143–147.

    Article  MathSciNet  MATH  Google Scholar 

  56. Davis, M.H.A., Capacity and cutoff rate for Poisson-type channels, IEEE Trans. Inf. Theory, 1978, vol. IT–26, no. 6, pp. 710–715.

    Article  MathSciNet  MATH  Google Scholar 

  57. Chernoyarov, O.V., Kutoyants, Yu.A., and Trifonov, A.P., On misspecifications in regularity and properties of estimators, Electron. J. Stat., 2018, vol. 12, no. 1, pp. 80–106.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work was supported by the Russian Foundation for Basic Research, project no. 20-11-50024.

Author information

Authors and Affiliations

  1. National Research University “Moscow Power Engineering Institute”, Moscow, 111250, Russia

    O. V. Chernoyarov

  2. Tomsk State University, Tomsk, 634050, Russia

    O. V. Chernoyarov, S. Dachian & Yu. A. Kutoyants

  3. Maikop State Technological University, Maikop, 385000, Russia

    O. V. Chernoyarov

  4. Université de Lille, Lille, 59000, France

    S. Dachian

  5. Le Mans Université, Le Mans, 72085, France

    Yu. A. Kutoyants

  6. Voronezh State University, Voronezh, 394018, Russia

    A. V. Zyulkov

Authors
  1. O. V. Chernoyarov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Dachian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu. A. Kutoyants
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. V. Zyulkov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to O. V. Chernoyarov, S. Dachian, Yu. A. Kutoyants or A. V. Zyulkov.

Additional information

Translated by V. Potapchouck

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chernoyarov, O.V., Dachian, S., Kutoyants, Y.A. et al. On Estimation Errors in Optical Communication and Location. Autom Remote Control 82, 2041–2075 (2021). https://doi.org/10.1134/S0005117921120018

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0005117921120018

Keywords

Search

Navigation