Skip to main content
SpringerLink
Log in

Two-Armed Bandit Problem and Batch Version of the Mirror Descent Algorithm

  • MATHEMATICAL GAME THEORY AND APPLICATIONS
  • Published:
Automation and Remote Control Aims and scope Submit manuscript

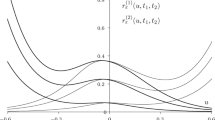
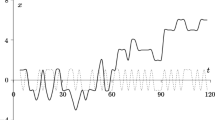
Abstract

We consider the minimax setup for the two-armed bandit problem as applied to data processing if there are two alternative processing methods with different a priori unknown efficiencies. One should determine the most efficient method and provide its predominant application. To this end, we use the mirror descent algorithm (MDA). It is well known that the corresponding minimax risk has the order of \( N^{1/2} \), where \( N \) is the amount of processed data, and this bound is order sharp. We propose a batch version of the MDA which allows processing data by packets; this is especially important if parallel data processing can be provided. In this case, the processing time is determined by the number of batches rather than the total amount of data. Unexpectedly, it has turned out that the batch version behaves unlike the ordinary one even if the number of packets is large. Moreover, the batch version provides a considerably lower minimax risk; i.e., it substantially improves the control performance. We explain this result by considering another batch modification of the MDA whose behavior is close to the behavior of the ordinary version and the minimax risk is close as well. Our estimates use invariant descriptions of the algorithms based on Gaussian approximations of income in the batches of data in the domain of “close” distributions and are obtained by Monte-Carlo simulation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.
Fig. 11.
Fig. 12.

Similar content being viewed by others

REFERENCES

  1. Borovkov, A.A., Matematicheskaya statistika. Dopolnitel’nye glavy: Uchebnoe posobie dlya vuzov (Mathematical Statistics. Additional Chapters: a Textbook for Universities), Moscow: Nauka, 1984.

    Google Scholar 

  2. Varshavskii, V.I., Kollektivnoe povedenie avtomatov (Collective Behavior of Automata), Moscow: Nauka, 1973.

  3. Gasnikov, A.V., Nesterov, Yu.E., and Spokoiny, V.G., On the efficiency of a randomized mirror descent algorithm in online optimization problems, Comput. Math. Math. Phys., 2015, vol. 55, no. 4, pp. 580–596.

    Article  MathSciNet  Google Scholar 

  4. Kolnogorov, A.V., Gaussian two-armed bandit and optimization of batch data processing, Probl. Inf. Transm., 2018, vol. 54, no. 1, pp. 84–100.

    Article  MathSciNet  Google Scholar 

  5. Kolnogorov, A.V., Gaussian two-armed bandit: limiting description, Probl. Inf. Transm., 2020, vol. 56, no. 3, pp. 278–301.

    Article  MathSciNet  Google Scholar 

  6. Nazin, A.V. and Poznyak, A.S., Adaptivnyi vybor variantov (Adaptive Choice of Options), Moscow: Nauka, 1986.

    Google Scholar 

  7. Nemirovskii, A.S. and Yudin, D.B., Efficient methods for solving high-dimensional convex programming problems, Ekon. Mat. Metody, 1979, vol. 15, no. 1, pp. 135–152.

    Google Scholar 

  8. Presman, E.L. and Sonin, I.M., Posledovatel’noe upravlenie po nepolnym dannym (Sequential Control Based on Incomplete Data), Moscow: Nauka, 1982.

    Google Scholar 

  9. Smirnov, D.S. and Gromova, E.V., Decision-making model under presence of experts as a modified multi-armed bandit problem, Mat. Teor. Igr Pril., 2017, vol. 9, no. 4, pp. 69–87.

    MATH  Google Scholar 

  10. Sragovich, V.G., Adaptivnoe upravlenie (Adaptive Control), Moscow: Nauka, 1981.

    MATH  Google Scholar 

  11. Tsetlin, M.L., Issledovaniya po teorii avtomatov i modelirovaniyu biologicheskikh sistem (Research on Automata Theory and Modeling of Biological Systems), Moscow: Nauka, 1969.

    MATH  Google Scholar 

  12. Auer, P., Using confidence bounds for exploitation-exploration trade-offs, J. Mach. Learn. Res., 2002, vol. 3, pp. 397–422.

    MathSciNet  MATH  Google Scholar 

  13. Auer, P., Cesa-Bianchi, N., and Fischer, P., Finite-time analysis of the multi-armed bandit problem, Mach. Learn., 2002, vol. 47, no. 2–3, pp. 235–256.

    Article  Google Scholar 

  14. Bather, J.A., The minimax risk for the two-armed bandit problem, in Mathematical Learning Models—Theory and Algorithms, Lect. Notes Stat., New York: Springer-Verlag, 1983, vol. 20, pp. 1–11.

  15. Berry, D.A. and Fristedt, B., Bandit Problems: Sequential Allocation of Experiments, London–New York: Chapman and Hall, 1985.

    Book  Google Scholar 

  16. Fabius, J. and van Zwet, W.R., Some remarks on the two-armed bandit, Ann. Math. Stat., 1970, vol. 41, pp. 1906–1916.

    Article  MathSciNet  Google Scholar 

  17. Juditsky, A., Nazin, A.V., Tsybakov, A.B., and Vayatis, N., Gap-free bounds for stochastic multi-armed bandit, Proc. 17th World Congr. IFAC (Seoul, Korea, July 6–11, 2008), pp. 11560–11563.

  18. Kaufmann, E., On Bayesian index policies for sequential resource allocation, Ann. Stat., 2018, vol. 46, no. 2, pp. 842–865.

    Article  MathSciNet  Google Scholar 

  19. Lai, T.L., Levin, B., Robbins, H., and Siegmund, D., Sequential medical trials (stopping rules/asymptotic optimality), Proc. Natl. Acad. Sci. USA, 1980, vol. 77, no. 6, pp. 3135–3138.

    Article  Google Scholar 

  20. Lattimore, T. and Szepesvari, C., Bandit Algorithms, Cambridge: Cambridge Univ. Press, 2020.

    Book  Google Scholar 

  21. Lai, T.L. and Robbins, H., Asymptotically efficient adaptive allocation rules, Adv. Appl. Math., 1985, vol. 6, pp. 4–22.

    Article  MathSciNet  Google Scholar 

  22. Lugosi, G. and Cesa-Bianchi, N., Prediction, Learning and Games, Cambridge: Cambridge Univ. Press, 2006.

  23. Robbins, H., Some aspects of the sequential design of experiments, Bull. AMS, 1952, vol. 58, no. 5, pp. 527–535.

    Article  MathSciNet  Google Scholar 

  24. Vogel, W., An asymptotic minimax theorem for the two-armed bandit problem, Ann. Math. Stat., 1960, vol. 31, pp. 444–451.

    Article  MathSciNet  Google Scholar 

Download references

Funding

The research by A.V. Nazin was supported financially by the Russian Science Foundation, project no. 16-11-10015. The research by A.V. Kolnogorov and D.N. Shiyan was supported financially by the Russian Foundation for Basic Research, project no. 20-01-00062.

Author information

Authors and Affiliations

  1. Yaroslav-the-Wise Novgorod State University, Novgorod, 173003, Russia

    A. V. Kolnogorov & D. N. Shiyan

  2. Trapeznikov Institute of Control Sciences, Russian Academy of Sciences, Moscow, 117997, Russia

    A. V. Nazin

Authors
  1. A. V. Kolnogorov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. V. Nazin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. D. N. Shiyan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to A. V. Kolnogorov, A. V. Nazin or D. N. Shiyan.

Additional information

Translated by V. Potapchouck

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kolnogorov, A.V., Nazin, A.V. & Shiyan, D.N. Two-Armed Bandit Problem and Batch Version of the Mirror Descent Algorithm. Autom Remote Control 83, 1288–1307 (2022). https://doi.org/10.1134/S0005117922080100

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0005117922080100

Keywords

Search

Navigation