Abstract
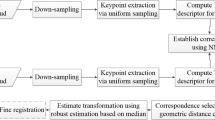
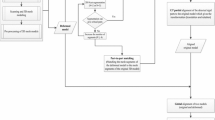
The registration of a 3D model over an image can be seen as the alignment of visual correspondences extracted from these two data. This is a challenging task and it is even more complex when the two images have a different modality. This paper introduces an approach that allows matching features detected in two different modalities: photographs and 3D models, by using a common 2D representation. Our approach is based on a modification of the Marching Cubes algorithm aiming to remove ambiguous cases without adding further calculations in each cube. We share the idea about the crucial importance of splitting the equivalence cases into two classes. Considering all the possible states inside/outside in the four corners of a cube side, indeed, there are only four non-trivial cases after eliminating those equivalences through the rotation. The obtained results allow us to validate the feasibility of the proposed methodology.












Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.REFERENCES
Kumar, T.S. and Vijai, A., 3D reconstruction of face from 2D CT scan images, Procedia Eng., 2012, vol. 30, pp. 970–977.
Cirne, M. and Pedrini, H., Marching cubes technique for volumetric visualization accelerated with graphics processing units, J. Braz. Comput. Soc., 2013, vol. 19, p. 09.
Newman, T. and Yi, H., A survey of the marching cubes algorithm, Comput. Graph., 2006, vol. 30, pp. 854–879.
Long, Z. and Nagamune, K., A marching cubes algorithm: application for three-dimensional surface reconstruction based on endoscope and optical fiber, Information (Japan), 2015, vol. 18, pp. 1425–1437.
Lorensen, W.E. and Cline, H.E., Marching cubes: a high resolution 3D surface construction algorithm, SIGGRAPH Comput. Graph., 1987, vol. 21, no. 4, pp. 163–169.
Durst, M.J., Letters: additional reference to marching cubes, Comput. Graph., 1988, vol. 22, no. 2, pp. 72–73.
Nielson, G. and Hamann, B., The asymptotic decider: resolving the ambiguity in marching cubes, Proc. 26th IEEE Conf. on Visualization, Tempe, AZ, Oct. 22–25, 1991, pp. 83–91.
Natarajan, B., On generating topologically consistent isosurfaces from uniform samples, Visual Comput., 1994, vol. 11, pp. 52–62.
Chernyaev, E.V., Marching cubes 33: construction of topologically correct isosurfaces, Tech. Rep., Inst. for High Energy Physics, 1995.
Custodio, L., Pesco, S., and Silva, C., An extended triangulation to the marching cubes 33 algorithm, J. Braz. Comput. Soc., 2019, vol. 25, p. 12.
Gong, F. and Zhao, X., Three-dimensional reconstruction of medical image based on improved marching cubes algorithm, Proc. Int. Conf. on Machine Vision and Human-Machine Interface, Kaifen, 2010, pp. 608–611.
Liu, S. and Peng, J., Optimization of reconstruction of 2D medical images based on computer 3D reconstruction technology, J. Digital Inf. Manag., 2015, vol. 13, pp. 142–146.
Olshanskii, M.A., Reusken, A., and Grande, J., A finite element method for elliptic equations on surfaces, SIAM J. Num. Anal., 2009, vol. 47, 3339–3358.
Chernyshenko, A.Y. and Olshanskii, M.A., An adaptive octree finite element method for PDEs posed on surfaces, Comput. Methods Appl. Mech. Eng., 2015, vol. 291, pp. 146–172.
Bonito, A., Nochetto, R.H., and Pauletti, M.S., Dynamics of biomembranes: effect of the bulk fluid, Math. Model. Nat. Phenom., 2011, vol. 6, no. 5, pp. 25–43.
Cacciari, M. and Salam, G.P., Dispelling the N 3 myth for the k t jet-finder, Phys. Lett. B, 2006, vol. 641, no. 1, pp. 57–61.
Ulrich, T., Rendering massive terrains using chunked level of detail control, in SIGGRAPH 2002 Super-Size It! Scaling up to Massive Virtual Worlds Course Notes, New York: ACM Press, 2002.
Nielson, G.M., Zhang, L., Lee, K., and Huang, A., Parameterizing marching cubes isosurfaces with natural neighbor coordinates, in Advances in Geometric Modeling and Processing, Chen, F. and Jüttler, B., Eds., Berlin, Heidelberg: Springer, 2008, pp. 315–328.
Van Gelder, A. and Wilhelms, J., Topological considerations in isosurface generation, ACM Trans. Graph., 1994, vol. 13, no. 4, pp. 337–375.
Farin, G.E., Curves and Surfaces for Computer-Aided Geometric Design: a Practical Code, 4th ed., Acad. Press, 1996.
Montani, C., Scateni, R., and Scopigno, R., A modified look-up table for implicit disambiguation of marching cubes, Visual Comput., 1994, vol. 10, pp. 353–355.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Hernández Farías, D.I., Cabrera, R.G., Fraga, T.C. et al. Modification of the Marching Cubes Algorithm to Obtain a 3D Representation of a Planar Image. Program Comput Soft 47, 215–223 (2021). https://doi.org/10.1134/S0361768821030051
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0361768821030051