Abstract
Many modern data science applications build on data lakes, schema-agnostic repositories of data files and data products that offer limited organization and management capabilities. There is a need to build data lake search capabilities into data science environments, so scientists and analysts can find tables, schemas, workflows, and datasets useful to their task at hand. We develop search and management solutions for the Jupyter Notebook data science platform, to enable scientists to augment training data, find potential features to extract, clean data, and find joinable or linkable tables. Our core methods also generalize to other settings where computational tasks involve execution of programs or scripts.
Keywords: data lakes, table search, interactive data science, notebooks
1. INTRODUCTION
The data lake has emerged as a schema-agnostic repository for data sources and analysis results (“data products”), providing centralized access to data. Typically, the data lake is an abstraction over a distributed file system or an object store. Data lakes offer strong data access benefits, but they generally do little to help a user find the most relevant data, understand relationships among data products, or integrate heterogeneous data sources or products.
Data lakes are used in many settings across the enterprise and within data science. We believe data lake management [32] becomes especially necessary in collaborative data science settings, as well as those in which data processing methodologies are changing. A folder/file hierarchy is inadequate for tracking data that is updated across versions, processed across (often similar) computational stages in a workflow, used to train machine learning classifiers, and analyzed by users. Data lakes were developed to promote reuse of data (and associated workflows) — but if users are unaware of what is available, or unable to trust what they find, they end up reinventing their own schemas, import processes, and cleaning processes. This not only leads to inefficiencies and redundant work, but also inconsistency in data processing, irregularity in data representation, and challenges in maintainability.
Just as good software engineering promotes modular, maintainable, and reusable software components, we need ways of promoting reusable units of data and processing. Towards this over-arching goal, we seek to help users find semantically related datasets to facilitate common data analytics tasks. Our work addresses interactive, “human-in-the-loop” settings in which data scientists are undertaking data discovery, wrangling, cleaning, and analysis tasks. We develop a general framework for supporting multiple measures of table relatedness, and build upon prior techniques developed for looking at data-value and data-domain overlap to find unionable [33] and joinable [9, 13, 45] tables, to find mappings to common schemas [19] and to profile data to find joinable tables [9, 13]. Juneau additionally considers the context and intent of the user — by searching over the provenance of data resources, and by allowing a user to specify what type of task they are performing.
We focus in this paper on tabular and “shallow” hierarchical data that can be imported into (possibly non-first-normal-form) relations: CSVs, structured files, external web resources, and R and Pandas dataframes. We hypothesize that during interactive data science tasks, users often want to search the data lake, not only by keyword, but using a table, to find other related tables. Our implemented query-by-table framework incorporates specialized relevance-ranking criteria to support data wrangling and training tasks.
We enable searching over the inputs and outputs of data science workflows, each comprised of discrete computational steps or modules. Juneau assumes workflows are specified as sequences of cells within computational notebooks, hosted for multiple users on the cloud, such as Jupyter Notebook/JupyterLab, Apache Zeppelin, or RStudio. (Our work generalizes to shell scripts or computational workflow systems [18, 31, 34], and it builds upon a recent demo [44] to focus on effective ranking.) We further assume that the output of each module should be stored in a data lake we manage, alongside its provenance [8]. As the user works with data, Juneau helps them find additional resources:
Augmenting training/validation data.
Often, data from the same or related sources is captured in multiple sessions (perhaps by multiple users). Given a table from one such session, a data scientist may wish to augment his or her data, to form a bigger training or validation set for machine learning.
Linking data.
Records in one database may have identifiers referencing entries in another database. Joining on these links brings in additional fields that may be useful to the user or to a machine learning algorithm. It can be helpful for users to know about such links that are implicit in the data.
Extracting machine learning features.
Data scientists often seek additional/alternative features for a given data instance. In a collaborative setting, one data scientist may perform specific feature engineering on a data set, while another may do it in a different way. It can be helpful for each scientist to see alternative feature engineering possibilities.
Data cleaning.
Given a widely used table, a data scientist may want to see examples of how the table is loaded or cleaned. This involves finding alternative tables derived from the same inputs, but perhaps with missing values filled in.
For the above scenarios, searching for tables by keywords [5, 38] or row values [47, 48] is inadequate: we need a broader notion of relatedness that may consider schema similarity, record-level overlap, description of data and workflows and similarity in the workflows that create or use specific tables. Tasks may involve more than searching for unionable [33] or joinable [9, 45] tables. Given the complexity of each of our target tasks, we develop a general framework for composing multiple measures of similarity, choose a tractable subset of features, and explore how to combine these to support new classes of search. We make the following contributions:
A framework for combining measures of table relatedness, which uses top-k, pruning, and approximation strategies to return the most related tables.
A basic set of measures of table relatedness that consider both row and column overlap, provenance, and approximate matching, for multiple use cases.
An implementation in Juneau, which extends Jupyter Notebook with table search capabilities.
Experimental validation of our methods’ accuracy and scalability, via objective measures.
Section 2 defines the table search problem and explains our approach. Section 3 proposes measures for table similarity and relatedness. Section 4 then develops algorithms for these measures and for querying for similar tables. In Section 5 we describe Juneau, which implements the query schemes proposed in this paper. We then experimentally evaluate the Juneau implementation in Section 6, before describing related work in Section 7 and concluding in Section 8.
2. FINDING RELATED TABLES
As data scientists conduct their tasks, if they could easily find related tables (or have these recommended to them as “auto-completions”) rather than re-creating new ones, this would help foster many of the benefits we associate with good software engineering. Dataset and schema reuse would ultimately make different data analysis processes more regularized, and it would also provide natural ways of leveraging common work on cleaning, curation, and standardization. In this section, we formalize our problem, first by providing more detail on the types of workflows and environments we target, then by outlining the objectives of table search.
2.1. Workflows, Notebooks, and Data
While most of our techniques apply to any general corpus of tables, we target a richer data lake environment, in which we can observe tasks, provenance, and updates across time. Juneau supports computational notebook software, such as Jupyter Notebook [36] and its successor JupyterLab, Apache Zeppelin, and RStudio. Within this environment, users are performing multiple computational steps over data; we consider the overall sequence of operations to be a (sometimes one-off and ad hoc) computational workflow. Computational notebook platforms directly capture workflows and data exploration by interleaving source code cells (code modules in a workflow, executed in an external interpreter or query system) with their outputs (in the form of rendered visualizations or tabular output). Such cells typically are appended to the notebook sequentially, preserving a type of history. Additionally, cells in the computational notebook often produce side effects by modifying state (variables whose values are set, and readable by the next cell to execute) or producing tables or files (which may be read by a future cell execution that may even occur in another notebook).
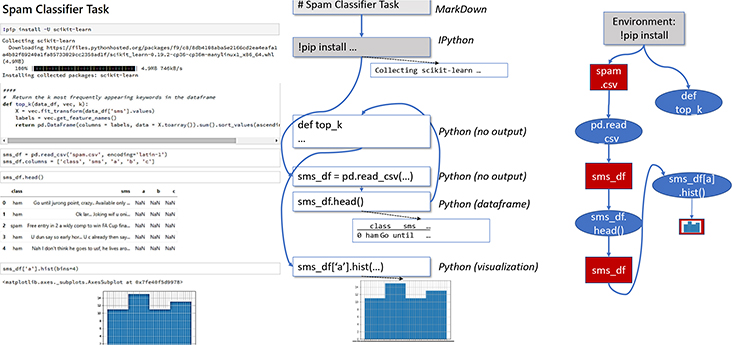
Computational notebooks are typically stored as semi-structured files, with limited data management. Notebook files do not fully preserve either the history of cell versions and outputs, nor the order in which cells were executed — which may result in non-reproducible notebooks. However, recent projects have introduced reproducible notebooks [7, 28, 37]. Juneau adopts a similar approach: it replaces the notebook software’s storage layer with a data lake storage subsystem, and replaces the notebook document with a broader object model. Our storage layer facilitates notebook storage and retrieval. Internally it also tracks versioning of the code cells, dependencies between cells that occur due to state sharing, and interactions between notebooks and the shell or terminal via files. Figure 1 shows the internal data model (right) of an example notebook (left). Juneau converts every notebook Ni into a workflow graph. We formalize this workflow graph WFi as a directed bipartite graph, in which certain data object nodes Di = {D1, …, Dm} are input to computational modules (in Jupyter, code cells), Mi = {M1, …,Mn}, via labeled directed edges.
Figure 1:
A computational notebook, data model, and workflow graph. Cells may be executed out of order, as encoded by blue lines in the data model. The workflow graph encodes cell dataflow dependencies.
Each module in Mi produces output data objects (set Di), which can be inputs to other computational stages. In Juneau our focus is on data objects that can be represented in (possibly non-1NF) tables. This includes input files read by the notebook, formatted text (Markdown) cells, and outputs (files, text, images). Edges between data objects and computational modules are labeled with the names of the program variables associated with those objects.
2.2. Searching the Lake
The problem of finding related tables in a data lake has multiple dimensions. First, there are a variety of different “signals” for table relatedness. For instance, in some settings, we may have shared values or keys; in others, the data may be complementary and thus have no value-overlap at all. Second, there are multiple kinds of tasks, each with different criteria for what makes a table useful:
Augmenting training or validation data:
we seek tables with similar schemata, descriptive metadata and provenance, and compatible values and datatypes — such that the table can be mapped as input into the machine learning algorithm being used. Tables that bring many new rows are preferred.
Linking data:
we seek data that joins with the existing table, meaning we need to find a small number of common schema elements with high data overlap. Tables that bring new fields are preferred.
Extracting machine learning features:
machine learning features are generally acquired by running code over the contents of a table — the result resembles that of a join, in that it adds columns to each row. There are two major differences from the linking-data use-case: (1) the feature-extracted table will generally derive from a table with different provenance from the search table, (2) the feature-extracted table should typically have a superset of the columns (and the majority of rows) of the search table.
Data cleaning:
high-ranking tables should match the schema of the search table, and share most rows (as identified by key) and values. The cleaned table should derive from one with similar provenance to the search table, and generally will have fewer null values and unique values per column.
2.3. Juneau Functionality
To support the search types described above, Juneau must leverage multiple measures for each search type, and it should easily extend if new measures are proposed by future researchers or domain experts. Our system is given a search table S, a search type τ and relatedness function Relτ that combines multiple measures (defined in Section 3), and an indexed set of tables in a data lake. It seeks the k most related tables. Section 4 develops (1) scalable algorithms for computing our measures, (2) a top-k engine to combine them. We prioritize inexpensive, highly-selective measures to prune candidate tables; then compute additional measures as needed.
Of course, any search method that must compare the contents of the search table against a large number of existing tables will not scale. We not only use data sketching and profiling techniques as in prior work [9, 13, 45], but in Section 5 we develop techniques for incorporating profiling algorithms that can identify the semantics of certain columns by their value ranges and data patterns (e.g., countries, first names). We generalize this idea to profile tables that contain certain combinations of fields, e.g., a table of people and their IDs. We create an index from the profile tables to matching fields in other tables; if a search table matches against the profile table, it can also be transitively matched to these tables.
3. MEASURES OF TABLE RELATEDNESS
The previous section gave an overview on how different search classes are supported by combining multiple measures. In this section, we propose basic measures of relatedness or utility sim(S, T) between a given target table T and our current search table S. We defer implementation to the next section. Note that the set of potential measures for table relatedness is nearly unbounded, because many domain-and data modality-specific measures might be defined for different use cases. Thus, we provide a basic set of measures for common use cases, and the extensible Juneau framework can incorporate additional measures. We divide our basic metrics into measures of table overlap (at the row and column level), useful for finding tables with schemas that augment or join with our existing data; measures of new information (rows or columns) that favor tables that bring more information; and measures of provenance similarity that indicate semantic relatedness between datasets. Finally, while data cleaning is a vast field that often employs domain-specific techniques, we develop simple measures to detect the kinds of data cleaning often employed in Jupyter notebooks, which involve filling in missing values.
3.1. Matching Rows and Columns
Our starting point is a measure of similarity or overlap between tables that are similar, but not necessarily identical, by finding matches among sub-components (namely, rows and columns). Intuitively, the overlap between tables may be broken down into row- and column-level overlap. Row overlap captures overlapping data items (or in machine learning parlance, instances); column overlap seeks to capture commonality of schema elements. Both notions must be tolerant of small changes to schema and values.
To characterize row-level and column-level similarity between a pair of tables S and T, we introduce a relation mapping μ consisting of a key mapping and a schema mapping. Intuitively, when the pairs of attributes kS, kT in the key mapping are equal, we have a value-based match between the rows. Conversely, the schema mapping attributes mS, mT capture pairs of attributes that semantically correspond (not as part of the key). Inspired by schema matching literature [39], we distinguish between value-based and domain-based (in the sense of semantic types) techniques for finding relation mappings and computing table overlap.
3.1.1. Value-based Overlap.
We start with a measure the commonality between rows in the tables, which is obtained by finding shared values in a corresponding key mapping.
Overlap with Exact Matches.
For the problem of table row overlap, we start with a strong assumption of exact matching, which we will ultimately relax. Given two tables S, T, we seek a mapping μ that relates tuples s ∈ S, t ∈ T.
Definition 1 (Key Mapping).
If S and T overlap, we expect that there is at least one candidate key kS for relation S and kT for relation T, each containing n attributes, such that if , then we have functional dependency and .
We say establishes a bijective key mapping K between pairs and , for 1 ≤ i ≤ n.
Often, attributes that are not part of a candidate key are in fact mappable between pairs of relations S and T, so the mapping key attributes do not fully define the relationship between pairs of tuples. Moreover, even if the keys exactly match, the remaining attribute values may not. We thus consider more general methods of mapping columns that do not directly overlap in value.
3.1.2. Domain-based Overlap.
Domain-based overlap captures the columns that are drawn from the same domain, even if they do not have overlapping values. The simplest form of domain-based overlap is to leverage similarity of labels and compatibility of domains [39]. Another method is to use ontologies with known instances [33]. However, ontologies often have limited coverage, and may not capture common patterns in the data. Therefore, we propose a more general solution that we term data profiles.
Definition 2 (Data Profile).
Suppose we are given a particular domain d (where a domain might be, e.g., a name, a birthday). Given a column c, we denote the data profile of c with respect to d as Ψ(c, d), where Ψ(c, d) = {ψi(c, d)}i. Each ψi represents a set of features indicating column c’s values belong to domaind. Given c, d and a group of weights ω = {ωi}, for each ψi, there exists a function gi, such that gi ψi(c, d) predicts the likelihood that column c has domain d. Denote M(c, d) as the function that predicts column c is of domain d, .
We can then define the domain-based mapping as follows.
Definition 3 (Domain-based Mapping).
Let D = {dj} be a set of domains. Given table S, we define a domain mapping , where sj is in the schema of S, dj ∈ D, and we say sj belongs to domain dj, if M(sj, dj) > τ, where τ is a threshold.
Our implementation (Section 4.2.2) relies on user-defined data profile-detection functions called registered matchers, as well as basic value-range and uniqueness checkers, as predictors for whether given columns map to domains.
Leveraging the domain-based mapping, we introduce schema mapping between two tables. If we assume that the probabilities are independent and that we are looking for a single common domain between columns, then we can further define a measure of similarity between columns c and c′ as:
We can now find correspondences between pairs of attributes (sj, tj): we assume one-to-one correspondences between attributes [39], and select pairs sj, tj in decreasing order of similarity MS(sj, tj), only selecting each column at most once. This yields a schema mapping:
Definition 4 (Schema Mapping).
A schema mapping , where |mS ⊆ S| = |mT ⊆ T| = k, is a bijective mapping between pairs of attributes sj ∈ mS, tj ∈ mT, 1 ≤ j ≤ k. Initially we assume that the domains of mapped attributes sj, tj are the same, which we term direct schema mappings.
3.1.3. Relation Mapping.
We then define the relation mapping, which will be a parameter to a lot of our similarity measures.
Definition 5 (Relation Mapping).
A relation mapping between relations S and T, μ(S, T) is a four-tuple (mS, mT, kS, kT) such that |mS ⊆ S| = |mT ⊆ T|, |kS ⊆ mS| = |kT ⊆ mT|, is a schema mapping between S, T, and kS, kT form a one-to-one key mapping K.
The culmination of these definitions yields a measure that can estimate the similarity between two tables:
Definition 6 (Overlap with Relation Mapping).
Given two tables S, T and a relation mapping μ = (mS, mT, kS, kT) between the tables, we define two components: row similarity, , and column similarity, . As with [5, 13], we use Jaccard similarity for each component. First, we consider row overlap; given that kS → mS and kT → mT :
| (1) |
For column similarity, we consider the overlap between the schemata of S and T, denoted by vectors , .
| (2) |
3.1.4. Relaxed Overlap Conditions.
In real world datasets that are not controlled by a DBMS, key constraints are occasionally violated due to errors, data consistency issues, and joint datasets that have not been fully de-duplicated. Thus, exact value overlap may be too strong a constraint to find key fields and thus identify common rows. We thus relax our constraints to incorporate approximate key constraints, and extend the similarity metric.
Value-based Overlap with Approximate Matches.
Approximate functional dependencies have been heavily studied in the database literature, with a focus on practical algorithms for their discovery [6, 12, 22, 24, 42]. We leverage this work to define a similarity measure (the algorithm used to detect the approximate dependencies is orthogonal to our work).
If a dependency kS → S holds, then all tuples in S with a given value of kS must be identical. However, in an approximate setting some tuples may not satisfy kS → S. We can collect this portion of S into a subset Sn, where for each s ∈ Sn[kS], there exist multiple tuples in Sn.
Definition 7 (Approximate Key Constraints).
Given a candidate approximate key, , we define a factor to measure how well kS serves as a key of S. Adapting a metric proposed in Wang et al. [42], we measure the expected number of tuples in the table associated with each value of the approximate key, . Note that the factor is equal to 1 if an exact functional dependency holds. Formally, is defined as follows:
| (3) |
Thus, if , and , then we say kS is an approximate key of S.
Domain-based Overlap with Approximate Matches.
Just as we may consider approximate matches for values, it is also possible to have a relaxed notion of domain overlap: namely, in a hierarchy or lattice of different domains, column sj may map to domain d1, column tj may map to domain d2, and the two domains may relate to each other.
Definition 8 (Compound Domain Mapping).
A compound domain mapping , where , , is a mapping between attributes sj ∈ ms and domains dj ∈ md. If holds, we say mS belongs to a compound domain md. We can associate a domain precision precis(ms, md) to capture how precisely md describes the domain of ms; the precision of the most specific domain will be 1.0, and super-classes of this domain will have successively lower scores.
Definition 9 (Approximate Relation Mapping).
We define an approximate relation mapping to be a relation mapping μ(S, T) = (kS, kT, mS, mT), with an approximation factor, γ(S, T), based on how closely or precisely the mapped portions of the relations (approximately) satisfy kS → mS and kT → mT . Formally, γμ(S, T) is:
| (4) |
We then compute the overlap defined in Definition 6, using the approximate relation mapping.
3.2. Augmenting with New Information
Table similarity measures commonality between tables, but in a variety of cases we also want to find tables that bring in a substantial amount of new data instances (rows). Therefore, we propose two metrics to measure information gain.
Definition 10 (New Row Rate).
Given table S, candidate table T, and their approximate relation mapping μ(S, T) = (mS, mT, kS, kT), we define the new row rate of T as :
| (5) |
Definition 11 (New Column Rate).
Given table S, candidate table T, and their approximate relation mapping μ(S, T) = (mS, mT, kS, kT), we define the new column rate of T as :
| (6) |
A complementary direction explored by Kumar et al. [29] is whether joining a table to bring in additional features notably improves a classifier’s accuracy. As future work, we are interested in exploring whether their notion (which considers schema constraints and VC-dimension) can be adapted to our setting in a low-overhead way.
3.3. Measures for Shared Provenance
The above similarity measures focus on matching table content, i.e., instances and schema. However, tables may also have similarity of purpose or role: i.e., they may be produced by an identical or similar workflow (sequence of notebook cells). We begin with a variable dependency graph (as is used in source code dependency analysis), which captures the dependencies among variables in the computational notebook. We extract a subgraph for each variable as its provenance graph, and define similarity based on the edit distance between provenance graphs.
Definition 12 (Variable Dependency Graph).
A variable dependency graph of a notebook is a directed acyclic graph with labels on edges denoted as G = (V, E, F). V represents the vertices consisting of all variables detected in the notebook. F represents operations (functions) that are used on the input variables to generate the output variables. E(G) represents the labeled directed edges, and for any triple ⟨u, v, l⟩ ∈ E(G), where u, v ∈ V (G), and l ∈ F(G), it means that variable u depends on variable v via operator l. Note that, table dependency graph is generated by extracting the assignment relationships, variables and functions from the source code of the computational notebook. To extract all of the information, we parse the source code to an abstract syntax tree (AST).
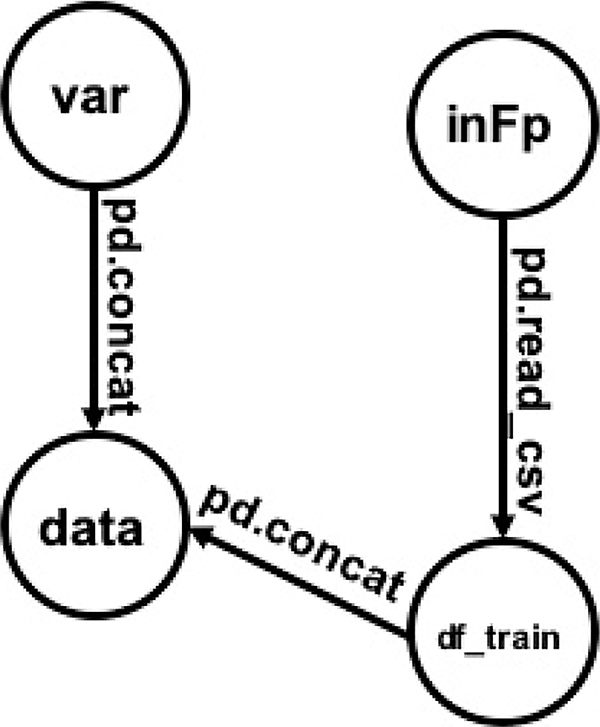
Listing 1: Example 3.1
inFp= “train.csv” df_train=pd.read_csv (inFp) var= “ SalePrice “ data =pd.concat ([df_train[“GrLivArea”],df_train[var]])
EXAMPLE 3.1.
See Listing 1 and Figure 2. The nodes represent the variables detected in the source code, including inFp, df_train, var, and data. The operators used here are functions such as pd.read_csv and pd.concat. The edges consist of all assignments in the source code. For example, data is output by running pd.concat on df_train and var. Therefore, it is connected by two edges with the same label from var, df_train respectively.
Figure 2:
Variable dependency graph
A variable dependency graph depicts how a variable depends on and affects other variables. Building upon this, we introduce a variable provenance graph for each variable.
Definition 13 (Variable Provenance Graph).
Given a variable dependency graph G = (V, E, F), a variable provenance graph PG(v) where v ∈ V is a subgraph of G, which describes all variables that affect v and their relationships.
Definition 14 (Variable Provenance Similarity).
The provenance similarity between two variables is defined via graph isomorphism. Given G = (V, E, F) and G′ = (V′, E′, F′), a graph isomorphism from G to G′ is a bijective function f : E → E′, s.t. ∀(u, v, l) ∈ E, ∃(u′, v′, l′) ∈ E′, s.t. u′ = f (u), v′ = f (v) and l = l′. Meanwhile, ∀(u′, v′, l′) ∈ E′, ∃(u, v, l) ∈ E, s.t. u = f −1(u′), v = f −1(v′) and l′ = l.
Provenance similarity between two variables va and vb, where va ∈ V and vb ∈ V′, is the graph edit distance [43], the most common measure of graph similarity, between PG(va) and PG(vb), denoted as edt(PG(va), PG(vb)). It is the number of edit operations in the optimal alignment that makes PG(va) reach PG(vb). The edit operation on a graph G is an insertion or deletion of a vertex/edge or relabeling of an edge. The costs of different edit operations are assumed to be equal in this paper.
Provenance similarity between S and T, simp(S, T), is thus:
| (7) |
We show an algorithm for computing provenance similarity in Section 4. Note that we only consider provenance for all definitions within the current notebook, and do not extend to imported packages or other files. As future work we will consider code analysis across source files.
3.4. Other Measures
3.4.1. Description Similarity.
The information of why and how a table was derived is also important when considering table similarity, especially when tables have limited row overlap. We consider the any descriptive information (metadata) about the source data, as well as the workflow used to produce the data, as a part of our similarity metrics, and we assume that they are all stored in a key-value form.
Examples of descriptive metadata are sketched in a recent vision paper [17], and may include the problem type, e.g., classification, regression, clustering; the domain of the source data, such as health care, finance, insurance; study conditions; text about workflow; etc.
We denote the description space of table S as Θ(S). Θ(S) = {(θi, vi, fi)|1 ≤ i ≤ N }, where θi represents a specific type of description, vi is the corresponding value of θi. Given another table T with its configuration space Θ(T), fi measures the similarity between vi and , where (θi, vi, fi) ∈ Θ(S) and .
Given table S, T and a description space, the description similarity simΘ(S, T) is defined as follows:
| (8) |
where wi is the weight for a specific feature, such that , and (θi, vi, fi) ∈ Θ(S) and .
3.4.2. Null Value Reduction.
The number of null values in a column is an important signal when looking for data cleaning tasks, as a common cleaning operation is to fill in or impute missing values. We define the measure as follows:
Definition 15 (Null Value Decrement).
Given two tables S, T, and the relation mapping μ(S, T) = (mS, mT, kS, kT), the null value decrement is:
| (9) |
where Null(S) and Null(T) represent the number of null value entries in S and T respectively.
3.5. Composing Measures for Search
Section 2 described four typical classes of search. We now describe how our primitive measures from above can facilitate ranking for each search class.
3.5.1. Augmenting Training Data.
Tables with similar schema and provenance to the search table are likely to be useful as additional training data. Therefore, for this search class, given μ, we need a table T ∈ Σ with high and high . Meanwhile, we prefer tables that add new rows; therefore, the table should also have a high . Thus, given μ(S, T), Rel1(S, T) is defined as follows:
| (10) |
3.5.2. Linking Data.
Rather than looking for tables that have high column overlap, a data scientist often needs to find tables that augment or link to the current result. This is requires a joinable table, where we expect one-to-many (or in rare cases many-to-many) links between tuples.
Again, we assume the presence of a relation mapping μ(S, T) = (mS, mT, kS, kT). Here, however, we expect that either kS → S or kT → T, i.e., we can think of kS and kT as members of a key/foreign-key join. Therefore, in the first case, there will be a high row overlap between T and , which means will be high. In the second case, the high overlap will exist between S and , which means is high. Formally, given tables S, T and a relation mapping μ(S, T) = (mS, mT, kS, kT), Rel2(S, T) is:
| (11) |
3.5.3. Extracting Machine Learning Features.
Feature extraction will typically produce tables that preserve their inputs’ keys and other columns, but add more columns. We look for tables with high and high or high , but with low simp(S, T). Formally, Rel3(S, T) is:
| (12) |
3.5.4. Data Cleaning.
Compared with the search table, the output of data cleaning usually matches the schema and shares most rows, but has some data-level differences. The most typical “signal” is a reduction in null values. Therefore, we require the table has high , high and high . Since data cleaning is usually combined with other steps, we also require the alternative data cleaning steps should share common provenance, which means it also require a high simp(S, T). Formally, given μ(S, T), Rel4(S, T) can be defined as follows:
| (13) |
Summary of similarity measures.
We summarize our measures and their relative importance to each search class in Table 1. Note that we always add simΘ(S, T), the description similarity, to each measure: we consider it a strong indicator if tables were created by the same organization, belong to the same domain, or serve the same project.
Table 1:
How different measures correspond to different search classes.
| Search Class | |||||||
|---|---|---|---|---|---|---|---|
| Augmenting Training/ Validation Data | N/A | ++ | ++ | ++ | N/A | N/A | + |
| Linking Tables | ++ | N/A | N/A | N/A | N/A | N/A | + |
| Extracting Features | ++ | N/A | - - | N/A | ++ | N/A | + |
| Alternative Data Cleaning | ++ | ++ | + | N/A | N/A | ++ | + |
4. QUERYING FOR RELATED TABLES
Leveraging the similarity metrics and search classes of the previous section, we now develop algorithms for finding related tables. We must identify the best relation mapping between the source table S and the candidate table T (Section 4.2) and compute components of the table relatedness score (Section 4.3). Once we have relatedness scores, we must compute the top-k results using effective pruning and indexing strategies (Section 4.4). We start with an overview of how ranked query processing (top-k search) works.
4.1. Overview of Top-k Search
The top-k query processing problem involves computing as few results as possible to return the highest-scoring results. This longstanding problem in query processing typically sets a threshold on remaining answers and returns values scoring above this [10, 23]. The challenge lies in using the measures with the highest selectivity/cost trade-off to “drive” the computation and prune many potential matches; then evaluating the remaining measures to refine our ranking.
We divide our basic measures in Table 1 into two categories, based on whether they depend on finding the relation mapping μ. Typically, detecting relation mapping is more time-consuming than other measures, i.e., simp(S, T) and simΘ(S, T), since the provenance graph of a table and the metadata of the notebook or the dataset are proportionally small. Therefore, the relation mapping is the bottleneck when doing top−k search. Based on this observation, we leverage a threshold algorithmic framework to do top−k table search, whose idea is to leverage computationally efficient measures to prune the candidate tables, minimizing computation of the time-consuming parts (e.g., the relation mapping).
Ultimately, we must find a relation mapping between tables. To speed this up, we create indices to help quickly detect a mapping for part of a table’s schema, and then if necessary, we incrementally refine the full relation mapping detection. Since the partial relation mapping is efficient to compute, we can also fit this staged relation mapping strategy into our threshold based algorithmic framework.
4.2. Detecting Relation Mappings
Most of our similarity measures require the relation mapping as input. This requires us to detect a schema mapping at the domain-level , and subsequently derive a set of key mappings by looking at values within the mapped columns. In turn, finding the schema mapping involves estimating value-based overlap, then matching columns against data profiles to detect their domains.
4.2.1. Computing Value-based Overlap.
We use Jaccard similarity between pairs of columns, to determine their overlap score, MS(i, j):
| (14) |
where ( is the schema for table S) and . Alternatively, we could estimate similarity using sketches or LSH based approximation [14, 46] for scalability.
4.2.2. Computing Domain-based Overlap.
Value-based overlap is a strong signal that columns share the same domain, but sometimes different tables contain disjoint data values. As described previously, ontologies [33] are one method of determining common domains, but they are often unavailable or under-populated. To handle such cases, we propose two methods to identify columns’ domains.
Registered Matchers.
Leveraging an idea from schema matching [39], we pre-define a series of matching functions that can test if the column belongs to a specific domain. A typical example is to validate email address by regular expression. In Juneau, we also allow users to register their own matchers to match columns to specific domains. Our implementation, described in Section 6, supports matchers that check columns’ data types, unique values, value ranges, and common patterns. This is generally through a combination of value-range checking (e.g., for zip codes), pattern detection (e.g., for phone numbers or street addresses), and cross-checking across a dictionary (e.g., for common names).
Data Profiles.
More generally, we can develop algorithms that do data profiling to predict whether a column belongs to a domain, e.g., by testing for features as defined in Section 3: example features include columns’ data types, unique values, value ranges, and common patterns. Additionally, the outputs of the registered matchers above form additional features.
In our initial implementation of Juneau, we use Boolean-valued features, and then compute Jaccard similarity between the sets of features reflected in two sets of columns. This could be easily generalized to real-valued features.
We also generalize to look at co-occurring columns within the same schema; e.g., we may be more confident that we have a “last name” field if there is also a “first name” field. Here, we use a Naïve Bayes model to score the probability of c matching a column c′, and the characteristics in this case is ψi(c) = {c*}, where {c*} is the set of columns in the same table as column c. The score is computed as follows:
| (15) |
where , and , where n(c, c*) is the number of tables that contain both c and c*, and n(c) refers to the number of tables that contain c.
4.2.3. Relation Mapping.
Given matching scores between pairs of columns, we need to find the schema mapping between S and T. We find this schema mapping using integer linear programming [26], much as in prior work [16]. Formally, we denote xij as the binary variable indicating if is matched to , according to some attribute similarity function that may take schema or data into account [27, 39]. That is:
Here, we assume that each attribute in can be matched to at most one attribute in and vice versa. Thus, the objective is to find a mapping satisfying the constraints that can maximize the matching score as follows:
| (16) |
Finally, we use a greedy algorithm proposed by Papadimitriou [35] to get the best schema mapping.
4.2.4. Detecting keys and dependencies.
For a given schema mapping, the choice of key mappings determines which rows are mapped together, and thus it affects the relation mapping. Our goal is to find a key mapping K = (kS,kT ) with equijoin predicate , which maximizes the table overlap.
Since table overlap includes both row and column overlap, we denote the table overlap as:
| (17) |
where parameter β allows us to adjust the weight on row and column terms.
Next, we maximize (for some given parameter β and schema mapping ) to find the key mapping K between S and T. Formally,
| (18) |
Unfortunately, choosing the subset of a schema mapping as a key mapping to maximize the similarity is a variation of the classic, NP-hard subset-selection problem. Fortunately, the key mapping for two tables typically has a very small size, especially for linkable tables (key-foreign key joins seldom match on more than 2–3 keys). Therefore, we do not actually need to explore all subset combinations of attribute pairs from S and T, but limit the size of to be a small integer denoted as ks. Thus, the key mapping we are looking for is:
| (19) |
This optimization problem is tractable. We combine the chosen and K to form our relation mapping μ.
4.3. Estimating Provenance Similarity
Computing provenance similarity i.e., the graph edit distance between two variable provenance graphs (Section 3.3), is NP-hard [43]. In this section, we present an approximation algorithm to efficiently estimate the provenance similarity between two tables based on their variable provenance graphs. The basic idea of our estimation is to transform a graph structure to a multiset of star structures [43].
Star Edit Distance.
To estimate the provenance similarity between S and T, we first derive the corresponding variable provenance graphs, PG(S) and PG(T), respectively. The key idea of estimating the graph edit distance between PG(S) and PG(T) is representing each graph to be a set of star structures whose graph edit distance can be easily obtained. Based on the edit distances between star structures of PG(S) and PG(T), we can estimate the lower and upper bound of their graph edit distance, a.k.a their provenance similarity. In the following part, we first introduce the star structure and then elaborate on how to compute the edit distance between two star structures.
Definition 16 (Star Structure).
A star structure s is a labeled single-level, rooted tree which can be represented by a 3-tuple sr = (r, L, f ), where r is the root vertex, L is the set of leaves. Note that edges only exist between r and any vertex in L, and no edge exists among vertices in L. f is the labeling function on edges.
Given PG(T) = (V, E, F), we can represent it with a set of star structures, denoted as PGs(T) = {sr |r ∈ V }, where sr = (r, L, f ) and L ⊂ E, f ⊂ F.
Definition 17 (Star Edit Distance).
Given two star structures s1 = (r1, L1, f1) and s2 = (r2, L2, f2), we denote their star edit distance as sdt(s1, s2). Formally,
| (20) |
where , and Ψf represents the multiset of f.
Lower Bound of Edit Distance.
Based on the star representation of the variable provenance graph, we introduce a mapping distance between two star representations, and we leverage it to provide a lower bound on the graph edit distance between two variable provenance graphs.
Definition 18 (Mapping Distance).
Given two star representations PGs(S) and PGs(T ), assume that Υ is a bijective mapping between si ∈ PGs(S) and sj ∈ PGs(T ). The distance ζ between PGs(S) and PGs(T) is
| (21) |
Detecting an Υ that can minimize the mapping distance is also a combinatorial optimization problem, which is the same as detecting the schema mapping described in 4.2.3. Therefore, we use the same greedy solution to find Υ, so that we can compute the mapping distance efficiently.
Proposition 1. Given the mapping distance between PGs(S) and PGs(T), the provenance similarity between S, T satisfies:
| (22) |
Proof. Let P = (p1,p2, …,pl) be an alignment transformation from PG(S) to PG(T ), such that PG(S) = h0 → h1 → … → hl = PG(T), where hi−1 → hi indicates that hi is derived from hi−1 by executing cell pi. Following Definition 13, pi can be vertex or edge insertion or deletion, or edge relabeling. Let P consist of z1 edge insertions/deletions, z2 vertex insertions/deletions, and z3 edge relabelings; then the edit distance between PG(S) and PG(T ) is z = z1 + z2 + z3. Each edge insertion/deletion affects two vertices, increasing mapping distance by at most 2., every time it happens, only two vertices are affected, and for each vertex, it will at most increase a cost of 2 on mapping distance between star structures PGs(S) and PGs(T ). Therefore, the mapping distance between PG(S) and PG(T ) increases by at most 4z1. Given vertex insertions/deletions, the mapping distance remains the same. Given z3 edge relabelings, each of which affects two vertices, the mapping distance increases by at most 2z3. Thus:
| (23) |
In the following computation, we will use the lower bound of edt(PG(S), PG(T)) to estimate the provenance similarity between two given tables S and T.
4.4. Querying for Tables
Given a source table S and the techniques of this section, our table search algorithm seeks the top-k tables, which maximize the relatedness score for the user’s specific class of search. Without loss of generality, we assume that our goal is to find the k tables with highest table relatedness. Formally, given table S and the data lake , we seek top-k tables .
To return the top-k tables, a strawman solution is a form of exhaustive search: we take each table , find a relation mapping, then compute row and column overlap as well as the other relatedness components respectively, and ultimately rank our matches to return the top−k tables. Note that in the use cases we discussed in this paper, the most expensive parts are detecting relation mappings among the computational components.
Of course, the strawman solution is not efficient, because (1) it repeatedly computes schema mappings and candidate key dependencies without reusing any mappings or keys already detected, even though we may notice during indexing tables that some of the columns probably coming from the same domains; (2) in practice, most tables in the data lake are not related to the search tables along all relatedness metrics. Therefore, it is unnecessary to compute all relatedness components, especially the more time-consuming ones, for each candidate table. We may be able to quickly prune some tables from consideration.
Top-k query processing is a well-studied problem [23, 25, 30], with Fagin’s Threshold Algorithm [10] forming a strong foundation. Building upon the insights of reusing relation mappings and the top-k query processing literature, we use several key ideas to prune the search space.
4.4.1. Speeding up Relation Mapping.
As described in the last section, we create a data profile for each domain, which is either registered by the user, or detected when we store the table. In an index, we link all of the columns to their corresponding domains. Thereafter, we can leverage the data profiles as a means of finding tables with columns from the same domain. Moreover, we also have the workflows that generated the tables in the data lake, which we can also use to index tables.
Indexing via Data Profiles on Columns.
The data profile for each domain tests for features indicating that a column belongs to the domain; in turn, we can use the profile as an intermediary to other columns from this domain. We can thus directly use data profile information to accelerate schema mapping, without having to go through all columns from all tables. Specifically, given table S, we create data profile Ψ for each column , and match Ψ to the profiles of the domains already registered. Then, based on the matched pairs of profiles, the system will return the union of tables that are linked to the matched profiles, and we only consider valid relation mappings among those tables.
Indexing Sets of Columns via a Compositional Profile.
Considering that columns from particular domains often co-occur with certain other columns in the tables (e.g., address and postal code, full name and birth date) — if we can match one of them against a data profiles, the others are also very likely to be able to be matched with other columns in the table. Therefore, every time we search for related tables, we create an index entry mapping from a set of data profiles on columns to the matches within the current search table. As part of subsequent searches, we look for existing tables matched to the same set of columns’ data profiles — accelerating the problem of finding a relation mapping.
Indexing via Workflow Graph.
Another dimension by which we can index tables is through workflow steps. We encode each variable and each unique notebook cell as a graph node. The consecutive cells are linked and we further link each variable to the notebook cell it belongs to. Note that we only keep notebook cells with unique code, therefore the cells shared by different notebooks will become the nodes connecting different notebooks. Then, we can index all the tables that are derived by connected workflow steps. Indexing via the workflow graph can improve the detection of a relation mapping. We can trace through the workflow to find when two different tables actually originated from the same source; and from this, we can determine if columns match even if they are renamed! In future work we will explore alternative levels of granularity, using code analysis to break cells into smaller code blocks.
4.4.2. Staged Relation Mapping Detection.
As described above, we now have three indices to detect schema mapping: the data profile index on columns, the compositional profile index on co-occurring sets of columns, and the workflow graph index. In this section, we combine them using a staged relation mapping detection algorithm.
Stage 1: Matching by data profiles.
Specifically, given table S, we try to match each column against all registered data profiles. If one of the domains is matched, we continue to match additional columns , where i ≠ j to other domains, if these are connected via a compositional index. We return the union of tables linked by those matched domains, denoted as Σ*.
Stage 2: Matching by workflow index.
Then, for each candidate T ∈ Σ*, if T and S are linked via a workflow index, we further check if other columns can be matched. Lastly, if there are still columns of S and columns of candidate T that can not be matched, we will check if other columns can be matched through the technique of detecting value-based overlap proposed in Section 4.2.3.
4.4.3. Pruning.
Staged relation mapping can help us prune tables with minimal schema-level overlap, and reduce the times schema mapping (a cubic algorithm) must be invoked to detect value-based overlap. Additionally, since most tables are unrelated, they also have low scores along all relatedness metrics, which enables further pruning possibilities. Note that for each table T ∈ Σ*, if we have evidence that Rel(S, T) will be very low-scoring, we can short-circuit prior to searching for a full relation mapping or computing other time-consuming metrics.
Here, we leverage two strategies to develop our threshold based computational framework. First, if the relatedness computation needs detecting relation mapping, we will start with detecting mapping with indices. In this case, we can obtain a partial relation mapping, denoted as for each possible candidate T ∈ Σ*. Leveraging partial relation mapping, we can first compute the column overlap based metrics, i.e., and , which we can do sorted access when doing top−k search. Then, we can derive upper bounds for other relation mapping related metrics based on the partial relation mapping, and do random access when doing top-k search in a threshold style algorithm. Specifically, the upper bounds of relation mapping related metrics are as follows:
| (24) |
| (25) |
and,
| (26) |
Our second strategy is to use the related metrics that are inexpensive to compute, to prune the number of the tables for which we need to derive costly similarity metrics. Among the metrics we use in this paper, the least costly to compute are simp(S, T) and simΘ(S, T). Therefore, we can sequentially search over the top-scoring matches to those two metrics (“sorted access” in the Threshold Algorithm), and compute the expensive metrics on demand (“random access” in the Threshold Algorithm).
Approximation.
Leveraging the threshold algorithm as a framework also allows us an opportunity to use approximation. We can trade off precision for speed, by adapting the approximate version of Fagin’s Threshold Algorithm [10]. Here, we use an early stop strategy by introducing a new parameter α, with some value α > 1 specifying the required level of approximation. The algorithm will then stop when the kth biggest similarity of the tables remembered is higher than of the threshold, such that a table T′ not in the top−k set satisfies the condition that for every other table T inside the top-k set. This approximation relaxes the threshold test of our algorithm, making it possible to return approximate answers, which is much faster than our vanilla staged threshold algorithm.
5. SYSTEM IMPLEMENTATION
Our implementation of Juneau combines the measures of Section 4, within a middleware layer built between the Jupyter Notebook system and the PostgreSQL relational DBMS (10.9) and Neo4J (3.5.8) graph DBMS. The core of Juneau is comprised of approximately 5,000 lines of new code. Juneau links into Jupyter Notebook’s ContentsManager interface with PostgreSQL as its storage back end to store data and necessary indices, and links into Neo4j to store the relationship of tables, cells and notebooks.
Juneau provides two main services. The first one is table addition and indexing, which happens whenever a new Jupyter cell is executed. The table indexer creates a profile for each column of the table, then runs all registered matchers and domain detection algorithms to decide if the columns belong to the registered domains. The table and the matched columns will be linked to corresponding domains; new table contents will be appended to the profile, and meanwhile, we will also link the domains matched together via the compositional index. If none of the domains are matched, we will register the column as a new domain and store its profiles. We keep the top−K (in our experiment, K = 100) most-matched domains. Then, the indexer will also parse the notebook to generate the provenance graph of the table, and update other provenance information in the Neo4j Graph database. Lastly, the indexer stores the dataframe into PostgresSQL backend.
The second stage of Juneau, which hooks into Jupyter’s client-side user interface, is searching for related tables. The user selects a cell output table as a query, then specifies what type of table to look for; and our table search component retrieves the top−k related tables, according to the specified need described in Section 2. As described in Section 4, we use the staged threshold algorithm to do top−k search, and take the advantage of the table registry and caching to speed up the search process.
Periodically, we adjust the weights of our different search metrics via a hyperparameter tuning module. Given a manually labeled set of queries, we run Bayesian Optimization [2], a popular method for machine learning hyperparameter selection. We choose hyperparameter values that maximize our scores over the sample workload.
6. EXPERIMENTAL EVALUATION
In this section, we evaluate Juneau on real data science workflows with their source datasets, and compare it with several alternatives. We consider the following questions: (1) What is the execution-time speedup provided by our computational framework, including the threshold-based algorithm, data profiling and indexing? (2) How is the quality of the tables returned by our system in our proposed typical use cases, compared with those returned by alternatives such as keyword-based table search and LSH-based table search?
6.1. Experimental Setting and Overhead
We provide an overview of our experimental setup, including how we obtained the data, workloads and queries, and how we stored and indexed the tables derived from the workloads with other necessary information.
6.1.1. Data Sets and Workloads.
Our experiments use real data science workflows downloaded from kaggle.com. We collected 102 Jupyter Notebooks with their source data1, from 14 different Kaggle tasks and competitions. We divide these into three different categories: Machine Learning (ML), typically including workflow steps such as feature selection, feature transformation (construction) and cross-validation; Exploratory Data Analysis (EDA), typically including data cleaning, univariable study, multivariable study, hypothesis testing, etc.; Combined which includes both exploratory data analysis and validation of machine learning models. Table 2 describes some of the tasks and styles of data analysis.
Table 2:
Samples from experimental workload.
| ID | Task | Category |
|---|---|---|
| 1 | Predicting Sales Price kaggle.com/c/house-prices-advanced-regression-techniques |
EDA |
| 2 | Instacart Market Basket Analysis kaggle.com/c/instacart-market-basket-analysis/data |
EDA |
| 3 | Sentiment Analysis on IMDB Movie Review kaggle.com/renanmav/imdb-movie-review-dataset |
ML |
| 4 | Predicting Survival on Titanic kaggle.com/c/titanic | Combined |
We ran all of the notebooks in our repository, stored and indexed all variables output by each cell, if their type belonged to one of Pandas DataFrame, NumPy Array or List. In Juneau, tables and indices are stored in PostgreSQL, with provenance information captured in Neo4j. To index tables by profile, we created 10 matchers that used regular expression pattern matching and checking against dictionaries, and registered 59 domains as data profiles. 5 of the 10 matchers produced features relevant to our query workload: those for name, age, gender, country and sport; additional matchers were for last name, first name, email, address, ssn.
Storage and Indexing Overhead.
In total, our corpus includes over 5000 indexed tables, with 157k+ columns, whose size is just under 5GB. Data profiles and indices are updated when tables are indexed. The storage cost of data profiles is around 11.5MB and the provenance graph for tables is around 3.6MB. Indexing time per table was approximately 0.7 sec to index each table, with multiple indexing threads running in parallel to support interactive-speed user interactions.
6.1.2. Queries and Performance Metrics.
We develop workloads to study query efficiency and quality.
Query answering efficiency.
We divide our tables into small and large groups, based on whether cardinality is less than 105. We randomly sample 10 tables from each group (denoted as Q4 and Q5) at each round, issue each query, and compare the average search time with different algorithms.
Answer quality.
For each use case considered in this paper, we choose a notebook from our repository and choose a table from it to issue the query. Rather than using subjective measures of quality, such as labels or rankings we provide by hand over others’ data – we demonstrate effectiveness of our search results on the task being performed in the notebook.
To test augmenting training data, we choose a notebook from Task 3, and query the data in the notebook to find more training data. The original notebook tests the precision of the sentiment prediction, which we leverage as a baseline to evaluate the quality of the returning tables. When the top−k tables are returned, we inject a new line of code, replacing the query data with the returned tables, within the original notebook. Then we complete execution of the notebook, and measure the new precision of the prediction it generates.
To evaluate alternative feature extraction and data cleaning, we choose two notebooks from Task 4 and Task 1 for each case, respectively. Again, we query using a table (generated during feature engineering or data cleaning) from the notebook. As with the previous task, the original notebooks evaluate the precision of the prediction of a trained classifier. To evaluate our search results, we inject them to the notebook and use them to train the classifier. We compare the new precision versus the original.
Finally, to test our detection of linkable tables, we choose a notebook from Task 2, an EDA pipeline. We search using a table S which was used in a join with some table T. To evaluate the whether it makes sense to use a returned table R in a join, we check elsewhere in the notebook to see if R (or a table derived from it) is joined with T.
To measure overall quality, we use the mean average precision @ k (MAP@k), considering the top−k search.
6.2. Performance of Searching Tables
6.2.1. Search Efficiency.
We compare the full Juneau (SJ), which includes our threshold-based algorithm with data profiles and indices, against (1) brute-force search with LSH ensembles [46] (the parameter num_perm = 64) (L64), (2) our threshold based algorithm without data profiles and indices (TA), (3) TA only with data profiles (TA+P). Table 3 shows the running times of these different approaches as we vary k and the query sets (Q4 vs Q5), for each of our 4 search classes described above. Brute-force search is too slow, therefore we do not include it as a baseline. If the average running time is too long (>2300 seconds), we leave it as NF. Due to limited space, we omit keyword search over tables, which has very fast, nearly constant times (10s of msec).
Table 3:
Average running time (seconds) of returning top−k tables when searching for related tables
| top-k | Augmenting Training Data | Feature Extraction | Alternative Data Cleaning | Linking Data | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q4 | L64 | TA | TA+P | SJ | L64 | TA | TA+P | SJ | L64 | TA | TA+P | SJ | L64 | TA | TA+P | SJ |
| 1 | 919.4 | 1017 | 9.776 | 1.481 | 875.3 | 2036 | 8.288 | 2.332 | 947.7 | 1454 | 5.833 | 3.133 | 22.64 | 2252 | 14.67 | 3.033 |
| 5 | 919.4 | 1086 | 9.944 | 3.254 | 875.3 | 2149 | 8.624 | 2.336 | 947.7 | 1461 | 5.999 | 3.145 | 22.64 | 2252 | 15.077 | 3.261 |
| 10 | 919.4 | 1106 | 12.17 | 5.105 | 875.3 | 2228 | 9.744 | 3.302 | 947.7 | 1488 | 7.029 | 4.364 | 22.64 | 2252 | 15.510 | 4.169 |
| Q5 | L64 | TA | TA+P | SJ | L64 | TA | TA+P | SJ | L64 | TA | TA+P | SJ | L64 | TA | TA+P | SJ |
| 1 | 1755 | NF | 23.51 | 5.119 | 1691 | NF | 21.30 | 5.188 | 1871 | NF | 20.46 | 4.318 | 127.9 | NF | 22.44 | 4.246 |
| 5 | 1755 | NF | 23.86 | 5.290 | 1691 | NF | 21.87 | 5.417 | 1871 | NF | 20.87 | 4.517 | 127.9 | NF | 22.51 | 4.343 |
| 10 | 1755 | NF | 24.15 | 5.532 | 1691 | NF | 23.29 | 5.666 | 1871 | NF | 20.95 | 4.892 | 127.9 | NF | 22.73 | 4.864 |
This experiment shows the incremental benefits of each of our techniques. The basic TA starts by finding, in decreasing order of the measure simp(S, T), tables, before computing the other measures. TA+P prunes this by favoring matches to data profiles. SJ further includes workflow indices. Note that TA for detecting linkable data is the same as brute-force search, since we have to detect the relation mapping first. Across the search classes and query sets, Table 3 shows that neither the basic TA or the LSHE sketching techniques provide interactive-level response times. Data profiles (TA + P) provide orders-of-magnitude benefits, by efficiently detecting tables with partial mappings through the domains we detected during indexing. When Juneau can leverage workflow indices, this provides roughly another 1.5–6x speedup.
L64 uses LSH ensembles [46] to detect the matches between columns, or to detect a join domain and return the corresponding linkable tables. This uses fewer features than TA, so it is much faster, at the cost of quality, discussed in the next section. (Note that LSHE could also be combined with the other methods.)
In summary, data profiles and provenance indexing are critical to speeding up relation mapping, and complement our threshold based algorithmic framework.
6.2.2. Search Result Quality.
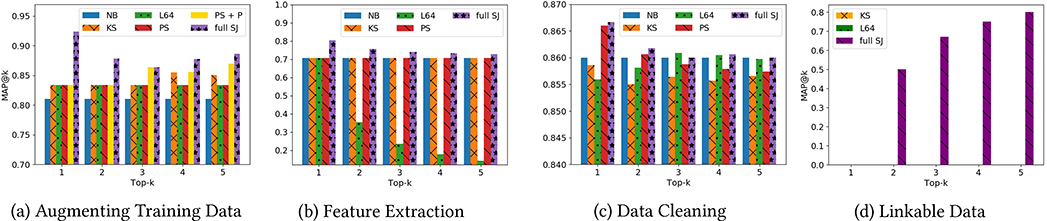
We compare Juneau (SJ) against the original notebook (NB), LSHE (L64, described above) and a keyword-based search baseline as might be provided by a search engine (KS). For the keyword-search baseline, we treat each table as a document, and each value as a word token. Each table is represented as a bag-of-words vector, and we use cosine similarity to compute relatedness. To incrementally evaluate the contributions of different measures to quality, we distinguish between “PS” (“partial Juneau”) which includes the row/column-similarity measures, and “full SJ” (also including notions of information gain and provenance similarity, as appropriate for the class of search). Figure 3 reports the impact of the returned tables on machine learning quality, for our different search classes. We discuss each class in sequence.
Figure 3:
MAP@K of tables returned by different search classes
Augmenting Training Data.
To evaluate the value of search results as additional training data, we compare the original precision of the trained classifier in the notebook (NB), versus the new precision obtained when training over the table returned. We only show MAP@k values above 0.70 for visual clarity. Figure 3 (a), shows that precision with results from Juneau is significantly better than our original baseline, as well as the alternate strategies. Even compared to PSJ, which only looks at row and column similarity, we see that our additional metrics greatly boost quality. To further understand the contribution of provenance and new data rate on providing different tables, we add a comparison PS + P, which is PS plus provenance similarity. We can observe from the figure that including provenance similarity has already provided some benefit compared with PS only.
Feature Extraction.
Figure 3 (b) searches for tables with extracted features. Here, L64 actually does poorly as we increase the value of k. Keyword search and PSJ show no improvement over the baseline. The full suite of Juneau measures provide slightly improved results, i.e., the additional features are beneficial to the machine learning classifier.
Data Cleaning.
Figure 3 (c) shows that data cleaning searches provide measurable but minor impacts on overall quality. Again the full Juneau metrics provide the best accuracy, even compared to PSJ’s overlap-based approach.
Linkable Data.
Finally, Figure 3 (d) shows quality for searches for linkable data. Here, both KS and L64 return overlapping content, rather than content that matches on key-foreign key relationships and contains “complementary” data – so they return no joinable results in the top-k. Juneau, for k = 2 and above, provides meaningful tables to join.
7. RELATED WORK
Data management for computational notebooks is an emerging area, with Aurum [13] focused on indexing and keyword search, and multiple efforts [7, 28, 37] addressing versioning and provenance tracking. Juneau builds similar infrastructure but focuses on search for related tables.
Table search over the web has been extensively studied. WebTables [4, 5] developed techniques for parsing and extracting tables from HTML, determining schemas, and supporting keyword search. WWT [38] augments lists of items using tables from the web, a special case of unionable tables. Fan et al. [11] used crowdsourcing and knowledge bases and Venitis et al. [41] used class-instance information to find web table sources for specific columns. Google Dataset Search [3] addresses search over web tables via their metadata.
The problems of linking and querying data in situ were considered in dataspaces [15], the Q System [40] and Belhajjame et al [1]. Data Civilizer [9, 14] maintains profiles on database tables to to discover links. Constance [19] exploits semantic mappings to mediated schemas to enable query reformulation. Google’s Goods [20, 21] indexes tables, supports annotations to sources, and provides faceted and keyword search plus the ability to browse provenance links. It uses LSH techniques to discover (and link) similar datasets. Nargesian et al. [32] focus on discovering unionable or joinable tables in a data lake. Our efforts are inspired by that work, but focus on exploiting our knowledge of tables’ provenance, defining different query classes and notions of table relevance, and supporting top-k queries.
8. CONCLUSIONS AND FUTURE WORK
This paper studied the problems of searching for related tables, for four types of tasks. We developed an extensible framework for efficient search with multiple similarity measures, and proposed novel indices to improve top-k performance. We evaluated using real Jupyter notebooks, and showed good search result quality and efficient performance. As future work, we hope to extend our work to handle nested data, and other data types that are not strictly tabular.
ACKNOWLEDGMENTS
The authors would like to thank the anonymous reviewers for their feedback. This work was funded in part by NSF grants III-1910108,ACI-1547360, and NIH grant 1U01EB020954.
Footnotes
CCS CONCEPTS
• Information systems → Federated databases;
Contributor Information
Yi Zhang, University of Pennsylvania, Philadelphia, PA.
Zachary G. Ives, University of Pennsylvania, Philadelphia, PA
REFERENCES
- [1].Belhajjame Khalid, Paton Norman W, Fernandes Alvaro AA, Hedeler Cornelia, and Embury Suzanne M. 2011. User Feedback as a First Class Citizen in Information Integration Systems.. In CIDR. 175–183. [Google Scholar]
- [2].Bolosky William J., Douceur John R., Ely David, and Theimer Marvin. 2000. Feasibility of a Serverless Distributed File System Deployed on an Existing Set of Desktop PCs. In Proc. Measurement and Modeling of Computer Systems, 2000 34–43. [Google Scholar]
- [3].Brickley Dan, Burgess Matthew, and Noy Natasha. 2019. Google Dataset Search: Building a search engine for datasets in an open Web ecosystem. In The World Wide Web Conference. 1365–1375. [Google Scholar]
- [4].Cafarella Michael, Halevy Alon, Lee Hongrae, Madhavan Jayant, Yu Cong, Wang Daisy Zhe, and Wu Eugene. 2018. Ten years of Webtables. Proceedings of the VLDB Endowment 11, 12 (2018), 2140–2149. [Google Scholar]
- [5].Cafarella Michael J., Halevy Alon Y., Wang Daisy Zhe, Wu Eugene, and Zhang Yang. 2008. WebTables: exploring the power of tables on the web. PVLDB 1, 1 (2008), 538–549. [Google Scholar]
- [6].Caruccio Loredana, Deufemia Vincenzo, and Polese Giuseppe. 2016. Relaxed functional dependencies — a survey of approaches. IEEE Transactions on Knowledge and Data Engineering 28, 1 (2016), 147–165. [Google Scholar]
- [7].Lucas AMC Carvalho Regina Wang, Gil Yolanda, and Garijo Daniel. 2017. NiW: Converting Notebooks into Workflows to Capture Dataflow and Provenance. In Proceedings of Workshops and Tutorials of the 9th International Conference on Knowledge Capture (K-CAP2017). [Google Scholar]
- [8].Cheney James, Chiticariu Laura, and Tan Wang Chiew. 2009. Provenance in Databases: Why, How, and Where. Foundations and Trends in Databases 1, 4 (2009), 379–474. [Google Scholar]
- [9].Deng Dong, Raul Castro Fernandez Ziawasch Abedjan, Wang Sibo, Stonebraker Michael, Elmagarmid Ahmed K, Ilyas Ihab F, Madden Samuel, Ouzzani Mourad, and Tang Nan. 2017. The Data Civilizer System.. In CIDR. [Google Scholar]
- [10].Fagin Ronald, Lotem Amnon, and Naor Moni. 2003. Optimal aggregation algorithms for middleware. J. Comput. System Sci 66(4) (June 2003), 614–656. [Google Scholar]
- [11].Fan Ju, Lu Meiyu, Beng Chin Ooi Wang-Chiew Tan, and Zhang Meihui. 2014. A hybrid machine-crowdsourcing system for matching web tables. In 2014 IEEE 30th International Conference on Data Engineering IEEE, 976–987. [Google Scholar]
- [12].Fan Wenfei, Geerts Floris, Li Jianzhong, and Xiong Ming. 2011. Discovering conditional functional dependencies. IEEE Transactions on Knowledge and Data Engineering 23, 5 (2011), 683–698. [Google Scholar]
- [13].Raul Castro Fernandez Ziawasch Abedjan, Koko Famien, Yuan Gina, Madden Samuel, and Stonebraker Michael. 2018. Aurum: A data discovery system. In 2018 IEEE 34th International Conference on Data Engineering (ICDE) IEEE, 1001–1012. [Google Scholar]
- [14].Raul Castro Fernandez Jisoo Min, Nava Demitri, and Madden Samuel. 2019. Lazo: A Cardinality-Based Method for Coupled Estimation of Jaccard Similarity and Containment. In 2019 IEEE 35th International Conference on Data Engineering (ICDE) IEEE, 1190–1201. [Google Scholar]
- [15].Franklin Michael, Halevy Alon, and Maier David. 2005. From databases to dataspaces: a new abstraction for information management. SIGMOD Rec. 34, 4 (2005), 27–33. [Google Scholar]
- [16].Gal Avigdor. 2011. Uncertain Schema Matching. Morgan and Claypool. [Google Scholar]
- [17].Gebru Timnit, Morgenstern Jamie, Vecchione Briana, Jennifer Wortman Vaughan Hanna Wallach, Daumeé Hal III, and Crawford Kate. 2018. Datasheets for datasets. arXiv preprint arXiv:1803.09010 (2018). [Google Scholar]
- [18].Goecks Jeremy, Nekrutenko Anton, and Taylor James. 2010. Galaxy: a comprehensive approach for supporting accessible, reproducible, and transparent computational research in the life sciences. Genome biology 11, 8 (2010), R86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Hai Rihan, Geisler Sandra, and Quix Christoph. 2016. Constance: An Intelligent Data Lake System In SIGMOD. ACM, New York, NY, USA, 2097–2100. 10.1145/2882903.2899389 [DOI] [Google Scholar]
- [20].Halevy Alon, Korn Flip, Natalya F Noy Christopher Olston, Polyzotis Neoklis, Roy Sudip, and Whang Steven Euijong. 2016. Goods: Organizing Google’s datasets. In Proceedings of the 2016 International Conference on Management of Data ACM, 795–806. [Google Scholar]
- [21].Alon Y Halevy Flip Korn, Natalya Fridman Noy Christopher Olston, Polyzotis Neoklis, Roy Sudip, and Whang Steven Euijong. 2016. Managing Google’s data lake: an overview of the Goods system. IEEE Data Eng. Bull. 39, 3 (2016), 5–14. [Google Scholar]
- [22].Huhtala Yka, Juha Kärkkäinen Pasi Porkka, and Toivonen Hannu. 1999. TANE: An efficient algorithm for discovering functional and approximate dependencies. The computer journal 42, 2 (1999), 100–111. [Google Scholar]
- [23].Ilyas Ihab F., Aref Walid G., and Elmagarmid Ahmed K.. 2003. Supporting Top-k Join Queries in Relational Databases. In VLDB. 754–765. [Google Scholar]
- [24].Ilyas Ihab F, Markl Volker, Haas Peter, Brown Paul, and Aboulnaga Ashraf. 2004. CORDS: automatic discovery of correlations and soft functional dependencies. In Proceedings of the 2004 ACM SIGMOD international conference on Management of data ACM, 647–658. [Google Scholar]
- [25].Ilyas Ihab F. and Soliman Mohamed. 2011. Probabilistic Ranking Techniques in Relational Databases. Morgan and Claypool. [Google Scholar]
- [26].Kim Jaewook, Peng Yun, Ivezik Nenad, Shin Junho, et al. 2010. Semantic-based Optimal XML Schema Matching: A Mathematical Programming Approach. In The Proceedings of International Conference on E-business, Management and Economics. [Google Scholar]
- [27].Konda Pradap, Das Sanjib, Doan AnHai, Ardalan Adel, Jeffrey R Ballard Han Li, Panahi Fatemah, Zhang Haojun, Naughton Jeff, Prasad Shishir, et al. 2016. Magellan: toward building entity matching management systems over data science stacks. Proceedings of the VLDB Endowment 9, 13 (2016), 1581–1584. [Google Scholar]
- [28].Koop David and Patel Jay. 2017. Dataflow notebooks: encoding and tracking dependencies of cells. In 9th USENIX Workshop on the Theory and Practice of Provenance (TaPP 17) USENIX Association. [Google Scholar]
- [29].Kumar Arun, Naughton Jeffrey, Patel Jignesh M., and Zhu Xiaojin. 2016. To Join or Not to Join? Thinking Twice about Joins before Feature Selection. In Proceedings of the 2016 International Conference on Management of Data Association for Computing Machinery, New York, NY, USA, 19âĂŞ34 10.1145/2882903.2882952 [DOI] [Google Scholar]
- [30].Li Chengkai, Kevin Chen-Chuan Chang Ihab F. Ilyas, and Song Sumin. 2005. RankSQL: Query Algebra and Optimization for Relational Top-k Queries. In SIGMOD. 131–142. [Google Scholar]
- [31].Bertram Ludäscher Ilkay Altintas, Berkley Chad, Higgins Dan, Jaeger Efrat, Jones Matthew, Lee Edward A., Tao Jing, and Zhao Yang. 2006. Scientific workflow management and the Kepler system. Concurrency and Computation: Practice and Experience (2006), 1039–1065. [Google Scholar]
- [32].Nargesian Fatemeh, Zhu Erkang, Miller Renée J, Pu Ken Q, and Arocena Patricia C. 2019. Data Lake Management: Challenges and Opportunities. Proceedings of the VLDB Endowment 12, 12 (2019). [Google Scholar]
- [33].Nargesian Fatemeh, Zhu Erkang, Pu Ken Q, and Miller Renée J. 2018. Table union search on open data. Proceedings of the VLDB Endowment 11, 7 (2018), 813–825. [Google Scholar]
- [34].Oinn T, Greenwood M, Addis M, Alpdemir N, Ferris J, Glover K, Goble C, Goderis A, Hull D, Marvin D, Li P, Lord P, Pocock M, Senger M, Stevens R, Wipat A, and Wroe C. 2006. Taverna: lessons in creating a workflow environment for the life sciences. Concurrency and Computation: Practice and Experience 18, 10 (2006), 1067–1100. [Google Scholar]
- [35].Papadimitriou Christos H. 1981. On the complexity of integer programming. Journal of the ACM (JACM) 28, 4 (1981), 765–768. [Google Scholar]
- [36].Perez Fernando and Granger Brian E. 2015. Project Jupyter: Computational narratives as the engine of collaborative data science. Retrieved September 11 (2015), 207. [Google Scholar]
- [37].Petricek Tomas, Geddes James, and Sutton Charles. 2018. Wrattler: Reproducible, live and polyglot notebooks. In 10th USENIX Workshop on the Theory and Practice of Provenance (TaPP 2018) USENIX Association. [Google Scholar]
- [38].Pimplikar Rakesh and Sarawagi Sunita. 2012. Answering Table Queries on the Web using Column Keywords. PVLDB 5, 10 (2012), 908–919. [Google Scholar]
- [39].Rahm Erhard and Bernstein Philip A.. 2001. A Survey of Approaches to Automatic Schema Matching. VLDB J. 10, 4 (2001), 334–350. [Google Scholar]
- [40].Talukdar Partha Pratim, Jacob Marie, Mehmood Muhammad Salman, Crammer Koby, Ives Zachary G., Pereira Fernando, and Guha Sudipto. 2008. Learning to create data-integrating queries. PVLDB 1, 1 (2008), 785–796. [Google Scholar]
- [41].Venetis Petros, Halevy Alon Y, Madhavan Jayant, Pasca Marius, Shen Warren, Wu Fei, and Miao Gengxin. 2011. Recovering semantics of tables on the web. (2011).
- [42].Wang Daisy Zhe, Dong Xin Luna, Sarma Anish Das, Franklin Michael J, and Halevy Alon Y. 2009. Functional Dependency Generation and Applications in Pay-As-You-Go Data Integration Systems. In WebDB. [Google Scholar]
- [43].Zeng Zhiping, Anthony KH Tung Jianyong Wang, Feng Jianhua, and Zhou Lizhu. 2009. Comparing stars: On approximating graph edit distance. Proceedings of the VLDB Endowment 2, 1 (2009), 25–36. [Google Scholar]
- [44].Zhang Yi and Ives Zachary G.. 2019. Juneau: Data Lake Management for Jupyter. Proceedings of the VLDB Endowment 12, 7 (2019). [Google Scholar]
- [45].Zhu Erkang, Deng Dong, Nargesian Fatemeh, and Miller Renée J. 2019. JOSIE: Overlap Set Similarity Search for Finding Joinable Tables in Data Lakes. In Proceedings of the 2019 International Conference on Management of Data ACM, 847–864. [Google Scholar]
- [46].Zhu Erkang, Nargesian Fatemeh, Pu Ken Q, and Miller Renée J. 2016. LSH ensemble: internet-scale domain search. Proceedings of the VLDB Endowment 9, 12 (2016), 1185–1196. [Google Scholar]
- [47].Zloof Moshé M.. 1975. Query-by-example: the invocation and definition of tables and forms. In VLDB ’75: Proceedings of the 1st International Conference on Very Large Data Bases 1–24. [Google Scholar]
- [48].Zloof Moshé M.. 1977. Query By Example: A Data Base Language. IBM Systems Journal 16(4) (1977), 324–343. [Google Scholar]