Abstract
Cognitive control allows behavior to be guided according to environmental contexts and internal goals. During cognitive control tasks, fMRI analyses typically reveal increased activation in frontal and parietal networks, and EEG analyses reveal increased amplitude of neural oscillations in the delta/theta band (2–3, 4–7 Hz) in frontal electrodes. Previous studies proposed that theta-band activity reflects the maintenance of rules associating stimuli to appropriate actions (i.e., the rule set), whereas delta synchrony is specifically associated with the control over the context for when to apply a set of rules (i.e., the rule abstraction). We tested these predictions using EEG and fMRI data collected during the performance of a hierarchical cognitive control task that manipulated the level of abstraction of task rules and their set-size. Our results show a clear separation of delta and theta oscillations in the control of rule abstraction and of stimulus–action associations, respectively, in distinct frontoparietal association networks. These findings support a model by which fronto-parietal networks operate through dynamic, multiplexed neural processes.
INTRODUCTION
Voluntary goal-directed behavior, called “cognitive control,” allows us to flexibly adjust our plans and quickly select actions, based on the context of our environment and our internal goals (Badre & D’Esposito, 2007; Koechlin, Ody, & Kouneiher, 2003; Miller & Cohen, 2001). The environmental context can be considered to provide rules, at various levels of abstraction, which are used to guide our actions (Bunge, 2004; Wallis, Anderson, & Miller, 2001). Such rules are thought to be represented in the lateral prefrontal cortex (LPFC; Badre & Nee, 2018; Bunge, 2004; Miller & Cohen, 2001). Previous studies of the role of LPFC in cognitive control have shown that it is involved in maintaining relevant information about abstract rules (D’Esposito & Postle, 2015; Curtis & D’Esposito, 2003) and integrating such information with inputs from posterior association and sensory cortices, which maintain lower-level sensory and stimulus information (Lorenc & Sreenivasan, 2021; Scimeca, Kiyonaga, & D’Esposito, 2018; Sreenivasan, Curtis, & D’Esposito, 2014; Fuster, 2001).
The LPFC, however, does not simply behave as a unitary controller. Rather, networks in LPFC are presumed to operate as a collective of specialized functional units, each with its own connections with parietal, temporal, and occipital regions, which flexibly interact to implement cognitive control (Menon & D’Esposito, 2022; Nee, 2021; Badre & Nee, 2018; Goldman-Rakic, 1988). Observations of patients with focal lesions and fMRI studies of healthy individuals have provided evidence of a caudal (posterior) to rostral (anterior) hierarchical organization of the representation of task-relevant information within LPFC, in which more abstract representations recruit more rostral areas (Szczepanski & Knight, 2014; Badre & D’Esposito, 2007, 2009; Badre, 2008; Koechlin & Summerfield, 2007; Koechlin et al., 2003). In contrast, in the posterior parietal cortices, representations become more abstract from rostral to caudal regions (Nee, 2021; Choi, Drayna, & Badre, 2018). Furthermore, these cortical gradients in LPFC and posterior parietal cortices are maintained in connectivity patterns with the dorsal striatum (Choi et al., 2018) and in thalamocortical projections from the thalamus (THA; Shine, Lewis, Garrett, & Hwang, 2023; Hwang & D’Esposito, 2022). The dynamics of neural activity within and between regions in these parallel functional cortical–subcortical networks to support hierarchical cognitive control remains underspecified and is the focus of this study.
The coordination of activity between a distributed network of areas may be enabled by neural oscillations (Buzsáki, 2006; Buzsáki & Draguhn, 2004). In particular, neural oscillations in the delta/theta band (~0.5–7 Hz) may serve as a mechanism for synchronizing distributed regions within functional networks, to support cognitive control processing (Helfrich, Breska, & Knight, 2019; Breska & Deouell, 2017; Helfrich & Knight, 2016). Time–frequency decoding procedures have shown that neural signals at frequencies between the delta and theta frequency range (1–8 Hz) carry information about task-relevant contexts, features, and response-rule representations (Cellier, Petersen, & Hwang, 2022). With increasing cognitive control, theta oscillations (~4–7 Hz) are typically generated over the medial frontal cortex (MFC), a phenomenon that is often referred to as “frontal-midline theta” (Cooper et al., 2019; Sauseng, Tschentscher, & Biel, 2019; Cavanagh & Frank, 2014; M. X. Cohen & Donner, 2013). The control of increasingly more complex rules seems to elicit neural oscillations that are even slower, in the delta-to-low theta frequency range (~1–5 Hz), and appear to be located more dorsolaterally compared with the frontal-midline theta (Formica, González-García, Senoussi, & Brass, 2021; Riddle, Vogelsang, Hwang, Cellier, & D’Esposito, 2020; de Vries, van Driel, Karacaoglu, & Olivers, 2018; Szczepanski et al., 2014).
In the current study, we tested the hypothesis that oscillations in the delta and theta band underlie different components of hierarchical cognitive control, mapping to distinct frontoparietal association networks. In a previous EEG study, we found power differences in frontal midline electrodes in the delta and theta band, distinctively associated with the level of abstraction of rules and the number of competing associations and rules (“set-size”), respectively (Riddle et al., 2020). Furthermore, the functional specificity of delta and theta oscillations for each component was confirmed by the results of a transcranial alternating current stimulation study, showing modulations of task performance in the cognitive control component (abstraction/set-size) expected to be associated with each low-frequency component of the noninvasive stimulation (Riddle, McFerren, & Frohlich, 2021). However, although these results were consistent with a “hierarchical account” for delta and theta oscillations, they did not characterize the temporal separability of these oscillations, nor their localization within separable functional brain networks, to support distinct levels of processing of hierarchical cognitive control.
To address these gaps, in the current study, we collected fMRI data during a hierarchical control task that manipulated both the level of task rules abstraction and their set-size (Badre & D’Esposito, 2007), as well as performed new analyses on the EEG data set we previously collected using the same task (Riddle et al., 2020). In the task, the abstraction manipulation served to capture changes in the neural dynamics associated with the level of abstraction of the task rules. On the other hand, the set-size manipulation served to characterize the neural dynamics associated with the control and selection between competing rules. In laboratory experiments like ours, these rules typically entail an association between certain characteristics or information of the stimulus and a corresponding correct behavioral response. Thus, we used the abstraction and set-size manipulations to respectively assess the “control of rule abstraction” and the “control of stimulus–action associations.” These two levels of control are proposed to be carried out in two distinct functional networks, one comprising brain areas that are more dorsolateral and distant from the sensory-motor cortex, and the other comprising areas that are more dorsomedial and closer to the sensory-motor cortex (sensorimotor-proximal).
The fMRI data set was used to define cortical ROIs, which were then used to perform EEG spectral analyses in these regions, as well as cortico–cortical connectivity analysis. Specifically, these analyses assessed delta/theta separability for the distinct levels of processing of hierarchical cognitive control and whether the functional networks underlying the control of rule abstraction and the control of stimulus–action associations are anatomically separable, or overlap. The fMRI data also allowed us to determine the involvement of subcortical structures in mediating cortico–cortical interactions at each level of cognitive control.
METHODS
Participants
We recruited in total 61 healthy human participants with normal or corrected-to-normal vision, and with no history of neurological or psychiatric conditions, to participate in two different studies at the University of California, Berkeley. The fMRI data were collected from 30 participants (aged 19–31 years, M = 22.1 years; 22/8 female/male). The EEG data were the same used in our previous study (Riddle et al., 2020) and were obtained from a different group of 31 participants (aged 18–34 years, M = 24.0 years; 18/13 female/male). The sample sizes were based on our previous work (Riddle et al., 2020). All participants gave written informed consent before the experimental session and received monetary compensation for their participation in the study. The study was approved by the Committee for the Protection of Human Subjects at the University of California, Berkeley.
Experimental Design
Within the hierarchical cognitive control task, we employed two behavioral subtasks named “response task” and “dimension task” (Badre & D’Esposito, 2007, 2009; Badre, 2008). The response task is a low abstraction task, in which participants have to respond based on a previously learned association between a visual stimulus (colored square) and an action (button response; Figure 1A). In the dimension task, which is characterized by a higher level of abstraction, participants have to decide whether two visual objects (shown inside a colored square) matched or not along one dimension (texture/shape; Figure 1B). Here, the relevant dimension of the objects is determined by the color of the square (context). In both the response and dimension tasks, we manipulated the number of competing associations (set-size) to match the performance in terms of accuracy between these two tasks (Riddle et al., 2020). The response task had either four (R4; low abstraction, low set-size) or eight (R8; low abstraction, high set-size) stimulus–response associations, whereas the dimension task had either one (D1; high abstraction, low set-size) or two (D2; high abstraction, high set-size) contextual representations.
Figure 1.
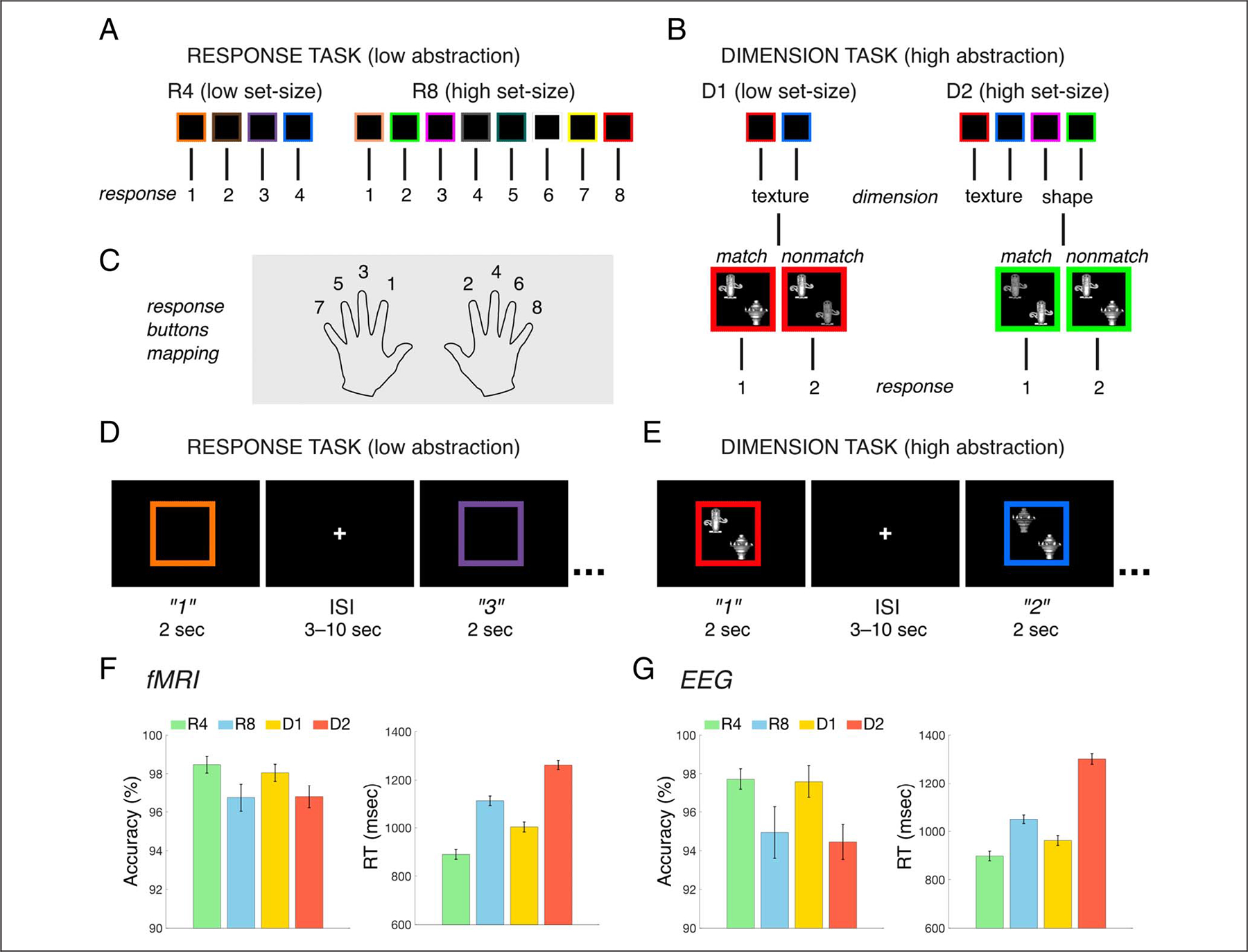
Experimental design. (A–B) Schematic representations of the rule sets in the response task (A) and dimension task (B). (C) Example of stimulus–response associations from one participant. (D–E) Schematic representation of example trial sequences in the response task R4 (D) and in the dimension task D1 (E). Quoted numbers represent the correct participant’s responses for the example mappings shown in A–B. Durations of stimulus presentation and ISI are reported in seconds. (F–G) Behavioral results for accuracy (%) and RT (msec) in the fMRI (D) and EEG (E) data set. Error bars indicate SEM.
In the response task, participants used their index and middle fingers on both hands for the low set-size condition (R4), and in addition, they used their ring and little fingers on both hands for the high set-size condition (R8; Figure 1A and C). In the dimension task, participants used their index finger on both hands (Figure 1B and C). In both the fMRI and EEG experiments, participants learned the specific sets of stimulus–action associations and contexts (Figure 1C) during a training session, performed before data acquisition. In the training session, practice blocks comprising 16 trials (using the same parameters as in the actual experiment; see below) were repeated until performance was above 70% accuracy. In the following experimental session, the participants performed eight blocks of trials (two blocks for each task), each block comprising 48 trials for 384 trials per experimental session. In each trial, the stimulus presentation lasted 2000 msec and the participants were instructed to provide their response while the stimuli were still on the screen (Figure 1D and E). A fixation cross was presented at the center of the screen during the ISI, which varied exponentially in duration within the range 3–10 sec. Twelve colored squares stimuli were used in the response task (four in R4 and eight in R8). Thirty-two stimuli, resulting from combining four colored squares with eight possible combinations of shape/texture of the two objects, were used in the dimension task. For each participant, a specific rule set was randomly selected from a predefined set of four mappings for the response task and two mappings for the dimension task, counterbalanced across participants, and it was kept the same for the two blocks of that task in the experimental session. The order of tasks over blocks was randomized in such a way that the first four and last four blocks contained all task conditions, and the same task was never performed back-to-back. For the D1 task, participants completed one block with texture and one block with shape as the relevant dimension of the objects, whose order was counterbalanced across participants. At the beginning of each block, a schematic instruction depicting the mapping reminded the participant of the relevant rule set for the upcoming block.
Data Acquisition and Preprocessing
fMRI
We collected the MRI data at the Henry H. Wheeler Jr. Brain Imaging Center (University of California, Berkeley) with a Siemens 3 T MAGNETOM Trio. We used a Siemens 32-channel head coil for data acquisition, using foam padding inside the head coil to reduce the participants’ head movements. The functional data were acquired with a T2*-weighted, gradient echo, EPI sequence (46 slices; voxel size = 3.0 mm isotropic; repetition time [TR] = 1500 msec; echo time [TE] = 25.8 msec; flip angle [FA] = 40°; Sensitivity Encoding–SENSE algorithm, multiband acceleration factor = 2). Functional data were acquired while the participants performed the tasks depicted in Figure 1, and their behavioral responses were collected using MRI-compatible four-button pads by Current Designs. The visual stimuli were presented using a modified MRI-compatible projector from Avotec, which was positioned at the rear of the scanner. The stimuli were projected onto a plexiglass screen with a nondispersing optical coating, and the participants viewed them through a custom-built mirror system, mounted on top of the head coil. We also acquired an anatomical whole-head image of the participants with a T1-weighted, magnetization prepared rapid acquisition gradient echo sequence (160 slices; voxel size = 1.0 mm isotropic; TR = 2300 msec; TE = 2.98 msec; inversion time = 900 msec; FA = 9°; parallel imaging via GeneRalized Autocalibrating Partially Parallel Acquisition, acceleration factor = 2). Both functional and structural MRI images were preprocessed using the Statistical Parametric Mapping (SPM12) toolbox (Penny, Friston, Ashburner, Kiebel, & Nichols, 2011). The functional images were first aligned to the mean of each session using a two-pass realignment procedure for motion correction. After realignment, the mean functional image was co-registered to the anatomical image using the normalized mutual information as the cost function. The standard segmentation procedure in SPM12 was employed to obtain individual masks for the cerebrospinal fluid (CSF) and white matter (WM), which were used to extract subject-specific time courses of CSF and WM signals. Finally, the images were normalized to the Montreal Neurological Institute-Hospital (MNI) stereotaxic space using a fourth-order B-spline interpolation, and the preprocessed data were spatially smoothed using a Gaussian filter (8-mm FWHM kernel).
EEG
We acquired the EEG data with a 64-channel BioSemi ActiveTwo EEG system, using a sampling rate of 1024 Hz. Four additional EOG electrodes were used to record the eye movements, and two more electrodes were used to record from the mastoids. Continuous EEG signals were first re-referenced to the mastoid electrodes average and then bandpass filtered 0.1–100 Hz using a two-way least-squares finite impulse response filter, implemented in EEGLab14 (Delorme & Makeig, 2004). Three-second epochs were extracted using the time window −1000 to 2000 msec around stimulus onset, for the stimulus-locked analyses, whereas the window −2000 to 1000 msec around RT was used to define epochs for the response-locked analyses. Epochs contaminated by excessive muscular activity artifacts were rejected by visual inspection (4.5% of trials, on average, across participants). Noisy EEG channels were also identified by visual inspection and interpolated using the average of the nearest neighbors electrodes. The number of interpolated channels was 0.48, on average, across participants (SD = 1.00, range = 0–3). An independent component analysis using EEGLab-extended infomax algorithm was employed to identify and remove eye blinks and other ocular activity artifacts. As a final step, a rereferencing to the common average reference was applied.
Univariate fMRI Analyses
We used two contrasts of interest, one for “abstraction” (high vs. low) and the other for “set-size” (high vs. low) to assess the control of rule abstraction and the control of stimulus–action associations, respectively. The comparisons were carried out exclusively on correct response trials. The statistical models for each participant were constructed using SPM12, under the general linear model assumptions (Friston et al., 1994). The first-level analysis was implemented using an event-related design, in which each event was modeled as a boxcar function whose duration was determined by the participant’s RT for that trial (variable epoch model; Grinband, Wager, Lindquist, Ferrera, & Hirsch, 2008). Regressors of interest were defined to model the correct response trials and incorrect trials in each task condition (R4, R8, D1, and D2), and a baseline (BL; pre-experiment rest period). The general linear model also included eight nuisance regressors that modeled the six motion realignment parameters generated by SPM12 (three for translations and three for rotations), as well as the mean signals of CSF and WM. The abstraction and set-size contrasts were used at the first-level individual analysis (two-tailed test). An additional set of contrasts was based on the difference between each task condition and BL (one-tailed test). In the second-level group analysis, the participants were modeled as random effects and statistical significance was assessed using voxel-wise t test comparison across participants (p < .001 uncorrected; minimum cluster-size of 50 voxels). The results of the abstraction and set-size contrasts were used to identify cortical ROIs (Table 1) for source-space reconstruction in EEG (see section Source reconstruction and power analyses in source-space, in the Methods section). The results of the contrasts between tasks and baseline were used to identify subcortical ROIs in the caudate nucleus (CN), putamen (PUT), and THA, which were successively used for fMRI connectivity analysis (see section Generalized psychophysiological interaction (fMRI), in the Methods section).
Table 1.
Results of the Univariate fMRI Analyses and Definition of the ROIs
| Anatomical Region | Centroid (x, y, z) | fMRI Cluster-peaks | Contrast |
|---|---|---|---|
|
| |||
| Left LPFC | −44.40, 20.00, 23.57 | −46, 24, 16 | High abstraction > Low abstraction |
| Right LPFC | 48.75, 27.72, 18.01 | 48, 28, 24 (36, 24, 26) | High abstraction > Low abstraction (High set-size > Low set-size) |
| Right frontal superior medial (SFGm) | 8.94, 36.11, 47.88 | 2, 32, 46 | High abstraction > Low abstraction |
| Right SFG | 20.80, 22.57, 49.85 | 21, 26, 48 | Low abstraction > High abstraction |
| Right SMA | 8.10, −1.75, 62.45 | 14, −2, 64 (4, 0, 52) | High set-size > Low set-size (Low abstraction > High abstraction) |
| Left PMd | −48.94, 2.31, 29.92 | −46, 4, 22 (−30, −14, 66) | High set-size > Low set-size (Low abstraction > High abstraction) |
| Right PMd | 44.04, 7.27, 47.66 | 48, 0, 34 (26, −16, 60) | High set-size > Low set-size (Low abstraction > High abstraction) |
| Left motor cortex (M1) | −51.11, −14.95, 35.19 | −48, −14, 34 | High abstraction > Low abstraction |
| Right motor cortex (M1) | 58.32, −11.36, 30.82 | 54, −6, 32 | High abstraction > Low abstraction |
| Left SPL | −24.24, −61.56, 54.95 | − 32, − 58, 54 (− 26, − 48, 66) | High set-size > Low set-size (Low abstraction > High abstraction) |
| Right SPL | 28.31, −59.47, 59.03 | 24, −42, 58 | Low abstraction > High abstraction |
| Right inferior parietal (IPL) | 37.62, −62.87, 42.37 | 28, −58, 46 | High abstraction > Low abstraction |
| Right CN | 12.03, 14.22, 4.84 | 12, 22, 2 (8, 6, 10) (6, 16, 6) | D2 > BL (R4 > BL) (D1 > BL) |
| Right PUT | 29.11, 0.97, 2.74 | 30, −2, −2 (24, 4, 8) | D2 > BL (R8 > BL) |
| Right THA | 11.59, −17.27, 10.00 | 10, −16, 10 (14, −18, 12) (16, −10, 10) | D2 > BL (R8 > BL) (D1 > BL) |
The column “Centroid (x, y, z)” provides the 3-D MNI coordinates of the centroid of each ROI. The column “fMRI cluster-peaks” provides the 3-D MNI coordinates of the spatially segregated cluster-peaks from the corresponding fMRI contrast. The column “Contrast” highlights the fMRI contrasts of interest whose significant results identified that ROI. Only the spatially segregated cluster-peak showing the biggest differences was used for ROI identification (the others are reported within parentheses).
EEG Analyses
Statistics
As in the fMRI, only correct response trials were included in the EEG analyses. Taking into account also the trials removed during preprocessing, the number of trials used for analysis, on average, across participants was 92.4 in R4 (SD = 4.8, range = 76–96), 88.1 in R8 (SD = 8.0, range = 56–96), 91.8 in D1 (SD = 6.8, range = 68–96), and 87.1 in D2 (SD = 7.4, range = 68–96). Statistical comparisons between high and low abstraction and between high and low set-size were performed using a cluster-based permutation approach, as implemented in FieldTrip (Oostenveld, Fries, Maris, & Schoffelen, 2011). The approach was based on a two-tailed dependent t test (df = 30; p < .05; number of permutations = 1000; p < .05 for the permutation test; multiple-comparisons correction by calculating the so-called, cluster-based test statistic and its significance probability via the Monte Carlo method; Maris & Oostenveld, 2007). The same settings were used in every statistical comparison, unless specified otherwise.
The space for clustering is specified in the description of each analysis (see below). A cluster-based permutation test accounts only for a difference between probability distributions in the two conditions overall; it does not allow for a precise inference on where in time, frequency, or space effects occur, but rather it only provides approximations of their extent (Sassenhagen & Draschkow, 2019; Maris & Oostenveld, 2007). Thus, in the results, we report the clusters in the observed data as descriptive statistics. The effect sizes of between-conditions differences were estimated using Cohen’s d (Cohen, 1992).
Time-varying Power Analysis and Irregular Resampling Auto-spectral Analysis
We performed a time-varying power analysis on sensor-space signals (on the scalp) separately for stimulus-locked and response-locked epochs. Time–frequency power estimation was performed using the Morlet wavelet transform with central frequency parameter equal to 6, at frequencies between 1 and 50 Hz (in unit increments). Zero-padding was used to solve the edge effects problem (Torrence & Compo, 1998). Spectral amplitudes from each contrast of interest were compared with the cluster-based permutation approach over time frames (in the 3-sec epoch), frequencies (1–50 Hz), and electrodes. Neighboring electrodes were defined using the “triangulation” algorithm implemented in FieldTrip, based on the 64-channel BioSemi cap.
To confirm the presence of distinct oscillatory peaks, in particular in the delta and theta band, we used the Irregular Resampling Auto-Spectral Analysis (IRASA; Wen & Liu, 2016), as implemented in FieldTrip. This analysis is of critical importance for removing the aperiodic component of the signal to isolate neural oscillatory activity. Specifically, IRASA was used to remove the 1/f component (aperiodic) from the power spectrum and derive power spectral estimates of rhythmic, periodic content, in the stimulus-locked 2 sec interval (0–2000 msec). Here, the power estimation was performed at frequencies between 1 and 50 Hz (in 0.5-Hz increments). To test for an effect of abstraction/set-size on the periodic power spectrum, we selected a priori frequency ranges in our data (delta: 2–4 Hz; theta: 5–8 Hz), based on the peaks identified by visual inspection of the periodic power spectra, and used a cluster-based permutation test over all electrodes (neighbors defined using “triangulation” algorithm, as before). We applied Bonferroni correction by taking the observed pperm-values and multiplying them by the number of comparisons made (m = 2, frequency ranges).
Source Reconstruction and Power Analyses in Source-space
The MNI template anatomical MRI was used to create a model of volume conduction for the forward problem. The template anatomy was first segmented to obtain border surfaces between scalp, skull, and brain (smoothing with 5 voxels FWHM Gaussian kernel); the volume conduction model was then created from these surfaces, using the boundary element method. The 3-D coordinates of the 64-channel BioSemi cap were aligned to the template head model to provide a model of the sensors. The template grid of regularly spaced points based on the MNI template anatomical MRI (number of solution points = 20173; spacing = 5 mm), provided in FieldTrip, was employed to define the grid of solution points for source reconstruction. The forward operator with unconstrained orientation (i.e., each solution point is modeled as three orthogonal equivalent current dipoles) was used to compute the leadfield matrix (solution of the forward problem). The solution of the inverse problem was obtained using the linearly constrained minimum variance beam-former (Van Veen, van Drongelen, Yuchtman, & Suzuki, 1997). The representative time series of each ROI were extracted using a singular value decomposition-based method (Rubega et al., 2019).
We used 12 cortical ROIs for source reconstruction, which were defined from the spatially segregated cluster-peaks previously obtained from the fMRI statistical analyses (see Table 1). Each cluster-peak was used as the center of a sphere (radius = 20 mm). All the solution points of the template grid falling inside the sphere were selected, and their tissue type was checked for consistency based on the automated anatomical labeling atlas parcellations defined in MNI space. This allowed us to keep only the solution points that belonged to the tissue-type of the atlas region and remove those belonging to other regions, uniquely identifying each ROI (i.e., no solution points were shared across ROIs). After extracting the source-reconstructed time series of each ROI, we repeated the wavelet-based, time–frequency power analysis. Here, the two contrasts of interest (abstraction/set-size) were assessed in source-space ROIs rather than scalp sensors; hence, clustering was performed over time frames, frequencies (1–50 Hz), and ROIs. Neighboring ROIs were defined based on the distance between their centroids in MNI space (maximum distance of 70 mm for defining neighbors).
In each ROI, IRASA was used to remove the 1/f component (aperiodic) from the power spectrum and derive power spectral estimates of rhythmic, periodic content. This analysis was performed in two stimulus-locked time intervals (“early” interval 200–900 msec; “late” interval 1000–1700 msec) and one “response-locked” interval (−600 to 100 msec). These time intervals of interest were defined based on the results of the previous time-varying power analysis in source-space. Specifically, the choice of the stimulus-locked late interval (1000–1700 msec) was motivated by the results showing increased power with abstraction in the delta band, and increased power with set-size in the theta band after ~1000 msec poststimulus; the FWHM of the time-collapsed frequency distribution of these between-conditions differences was 1088–1708 msec (see Figure 2D, in the Results section) and 980–1610 msec (see Figure 5E, in the Results section), respectively. A response-locked interval (−600 to 100 msec), matching in length with the previous one, was defined based on the results of the response-locked analysis showing alpha/beta-band power reduction with abstraction pre-response (FWHM −557 to 144 msec; see Figure 7B, in the Results section), where sustained negative differences in alpha/beta-band power were also observed between high and low set-size (see Figure 8). Despite the source-space results did not show low-frequency power differences at early latencies poststimulus, these were observed in sensor-space, in particular in the abstraction contrast (FWHM = 287–1990 msec; see Figure 2B, in the Results section); thus, a third interval, non-overlapping but matching in length with the other two, was employed to capture possible task-specific modulations in the power spectrum periodic components at early latencies poststimulus (200–900 msec). Similarly to the IRASA analysis in sensor-space (see previous section), in each interval, we tested for an effect of abstraction/set-size on the periodic power spectrum in the two frequency bands of interest, a priori selected, using a cluster-based permutation test over all ROIs (neighbors defined based on centroids’ distance of 70 mm), Bonferroni-corrected for m = 6 multiple comparisons (frequency ranges-by-time intervals).
Figure 2.
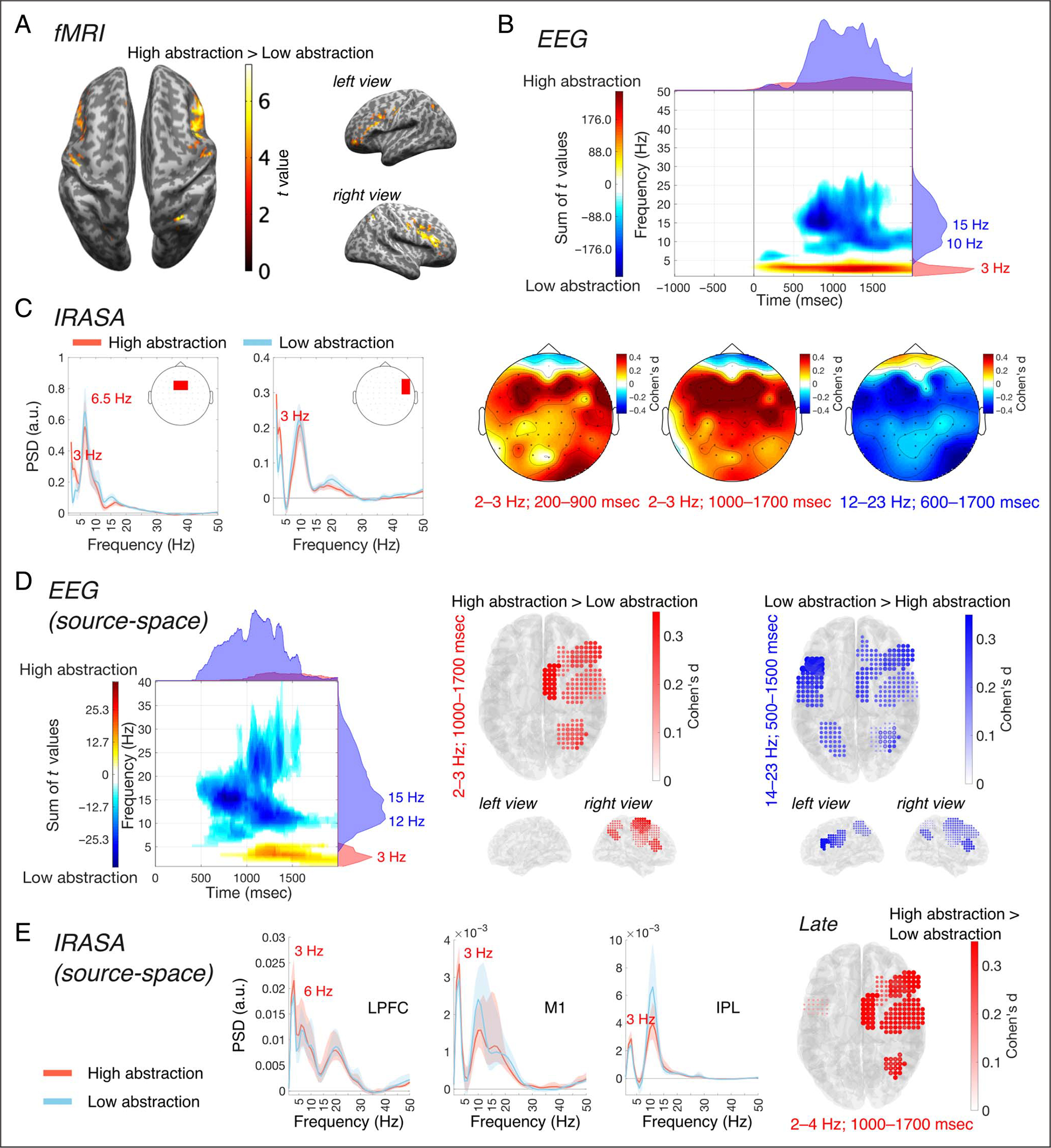
Univariate analyses for the abstraction contrast. (A) Results of the univariate fMRI analysis comparing high abstraction and low abstraction. (B) Results of the EEG power analyses comparing high abstraction and low abstraction (stimulus-locked) in sensor-space. The top figure shows the time–frequency distribution of the sum of between-conditions differences across electrodes, from the clusters found in the observed data, and the marginal plots on top and on the right represent, respectively, the time distribution (frequency-collapsed) and frequency distribution (time-collapsed) of those differences. The bottom figures show the scalp distribution of the effect sizes of the power differences. (C) Results of IRASA in sensor-space, in the groups of medial frontal electrodes (left), and right lateral frontal electrodes (right). (D) Results of the EEG power analyses comparing high abstraction and low abstraction (stimulus-locked) in source-space. The left figure shows the time–frequency distribution of the sum of between-conditions differences across ROIs, from the clusters found in the observed data, and the marginal plots on top and on the right represent, respectively, the time distribution (frequency-collapsed) and frequency distribution (time-collapsed) of those differences. The middle and right figures show the effect sizes of the differences in ROIs, superimposed over the MNI template anatomy. (E) Results of IRASA in source-space, in the right LPFC (left), M1 (middle), and IPL (right).
Figure 5.
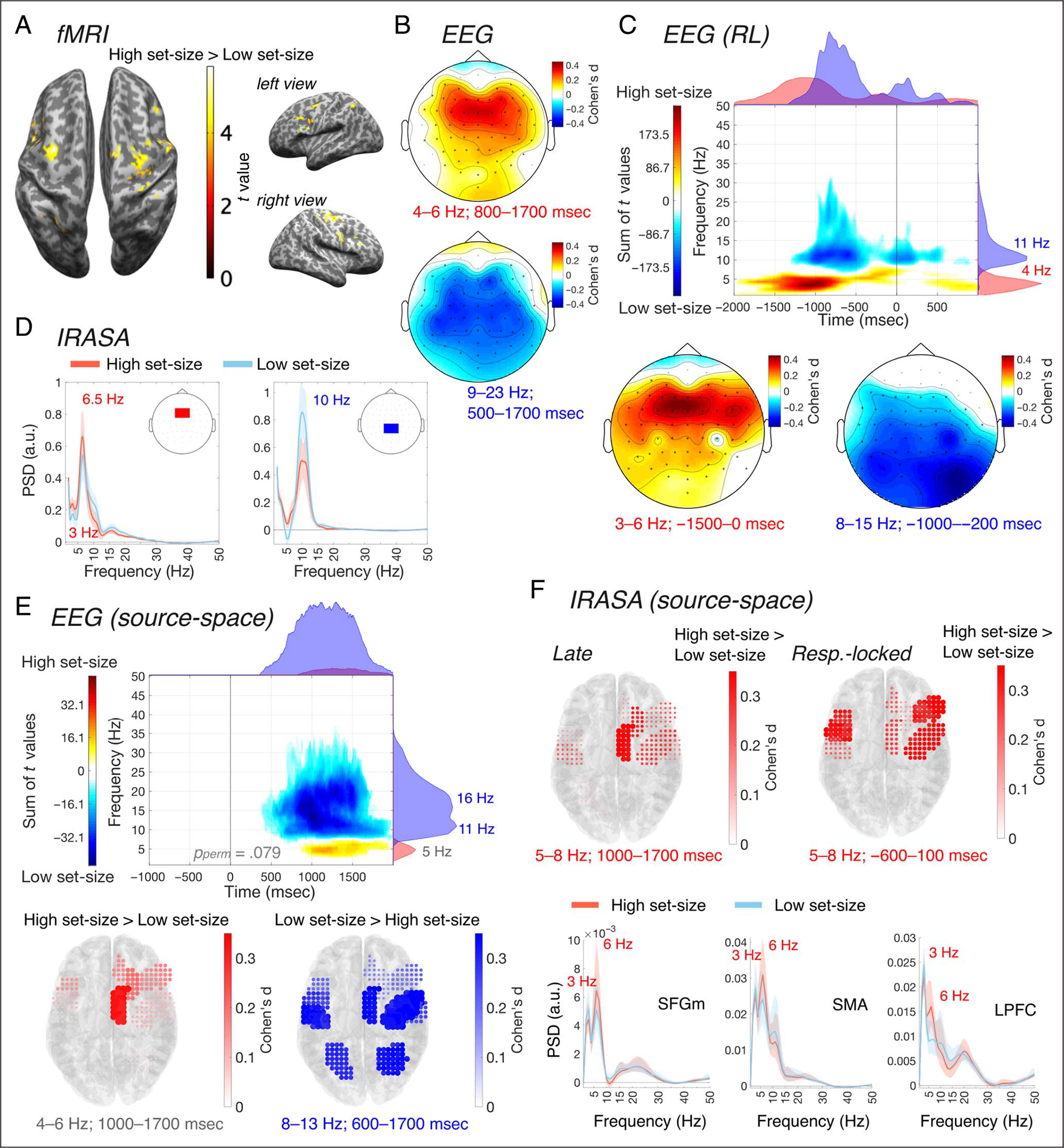
Univariate analyses for the set-size contrast. (A) Results of the univariate fMRI analysis comparing high set-size and low set-size conditions. (B–C) Results of the stimulus-locked (B) and response-locked (C) EEG sensor-space power analyses comparing high set-size and low set-size. In C, the top figure shows the time–frequency distribution of the sum of between-conditions differences across electrodes, from the clusters found in the observed data, and the marginal plots on top and on the right represent, respectively, the time distribution (frequency-collapsed) and frequency distribution (time-collapsed) of those differences. The other figures show the scalp distribution of the effect sizes of the power differences. (D) Results of IRASA in sensor-space, in the groups of medial frontal electrodes (left) and central-parietal electrodes (right). (E) Results of the EEG source-space power analyses comparing high set-size and low set-size. The left figure shows the time–frequency distribution of the sum of between-conditions differences across electrodes, from the clusters found in the observed data, and the marginal plots on top and on the right represent, respectively, the time distribution (frequency-collapsed) and frequency distribution (time-collapsed) of those differences. The middle and left figures show the effect sizes of the differences in ROIs from the positive cluster in the theta band (left) and the negative cluster in the alpha-band (right), superimposed over the MNI template anatomy. The positive cluster did not reach statistical significance in the cluster-based permutations testing (pperm = 0.079). (F) Results of IRASA in source-space, in the right SFGm (left), SMA (middle), and LPFC (right).
Figure 7.
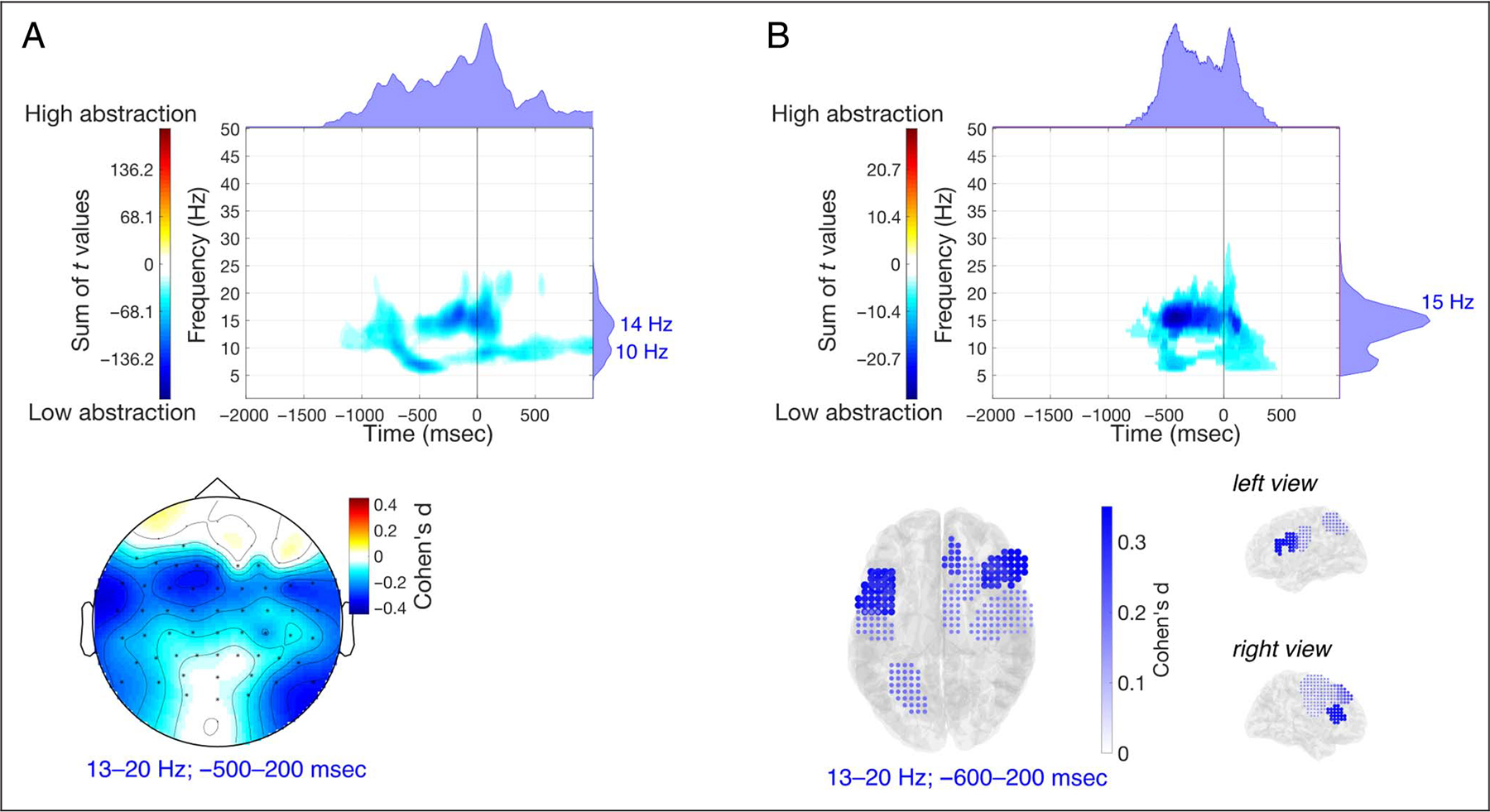
Response-locked analyses for the abstraction contrast. (A–B) Results of the EEG power analyses comparing high abstraction and low abstraction (response-locked) in sensor-space (A) and source-space (B). In each panel, the top figure shows the time–frequency distribution of the sum of between-conditions differences, from the clusters found in the observed data, and the marginal plots on top and on the right represent, respectively, the time distribution (frequency-collapsed) and frequency distribution (time-collapsed) of those differences. The bottom figures show the distribution of the effect sizes of the differences (either on the scalp or in ROIs).
Figure 8.
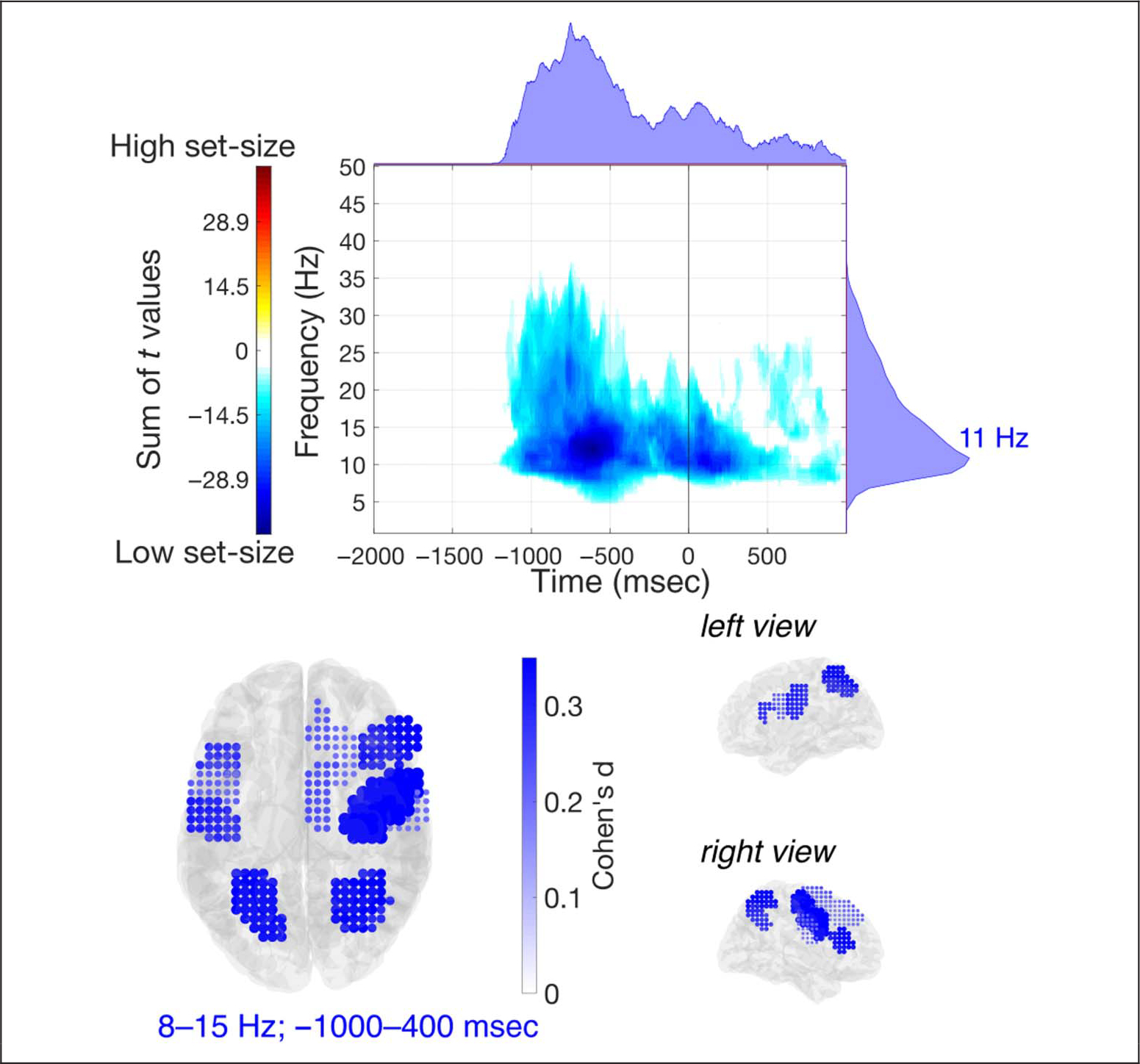
Response-locked analyses for the set-size contrast. Results of the EEG power analyses comparing high set-size and low set-size (response-locked) in source-space. The top figure shows the time–frequency distribution of the sum of between-conditions differences, from the clusters found in the observed data, and the marginal plots on top and on the right represent, respectively, the time distribution (frequency-collapsed) and frequency distribution (time-collapsed) of those differences. The bottom figures show the distribution of the effect sizes of the differences (in ROIs).
Connectivity Analyses
Nonparametric Granger–Geweke Causality (EEG)
We performed an EEG connectivity analysis in the early (200 to 900 msec, stimulus-locked), late (1000 to 1700 msec, stimulus-locked), and response-locked (−600 to 100 msec) time intervals of interest. In each interval, frequency domain measures of Granger–Geweke causality (Geweke, 1982) were derived from the spectral estimates of that interval, by using a multivariate method based on nonparametric spectral factorization (Pagnotta, Dhamala, & Plomp, 2018; Wen, Rangarajan, & Ding, 2013; Dhamala, Rangarajan, & Ding, 2008a, 2008b). This approach allowed us to derive the directed functional connections between ROIs from their source-reconstructed time series. Greater differences from the source-space power analyses were found in the right hemisphere (see Results section); thus, we analyzed only the connections between ROIs in that hemisphere. Statistical tests were performed on the graph measures of out-degree (sum of outgoing connections, i.e., each ROI as sender) and in-degree (sum of incoming connections, i.e., each ROI as receiver) over cortical ROIs, respectively in the delta (2–3 Hz) and theta (4–6 Hz) bands for the abstraction and set-size contrasts. Post hoc analysis for which specific connections served as the primary drivers for the significant roles of functional senders (higher out-degree) and receivers (higher in-degree) was carried out using a one-tailed dependent t test in the direction of interest (out for sender or in for receiver; p < .05 uncorrected).
Generalized Psychophysiological Interaction (fMRI)
We performed a functional connectivity analysis using fMRI data to assess the involvement in cognitive control of subcortical structures like the dorsal striatum (CN, PUT) and THA, and of subcortical and cortical–subcortical connectivity, which cannot be reliably evaluated using EEG. The fMRI connectivity analysis was performed only on right hemisphere ROIs (eight cortical and three sub-cortical), where the majority of abstraction and set-size modulations were observed in EEG analyses (see Results section). The data from each ROI were extracted using the spherical ROI approach, in which a sphere (radius = 5 mm) was centered at the xyz MNI coordinates specified by the centroid of each ROI in Table 1. The ROI-to-ROI connectivity was measured using the generalized psycho-physiological interactions (gPPI; McLaren, Ries, Xu, & Johnson, 2012), as implemented in the CONN toolbox (Nieto-Castanon, 2020; Whitfield-Gabrieli & Nieto-Castanon, 2012), by using the two contrasts of interest for abstraction and set-size. Each analysis was restricted in a data-driven manner to the subset of ROIs that showed significant functional interactions from the previous EEG connectivity analysis (see Results section), and statistical testing was based on a one-tailed dependent t test (p < .05 uncorrected). The CONN toolbox was also used to make the plots of the results.
RESULTS
Behavioral Data Analyses
We manipulated the level of abstraction of the task rules, as well as their set-size, and investigated the impact of these task demands on performance accuracy. For the participants who completed the fMRI session (Figure 1F), the mean accuracy was equal to 98.47% in R4 (SD = 2.38%), 96.75% in R8 (SD = 3.90%), 98.05% in D1 (SD = 2.44%), and 96.80% in D2 (SD = 3.18%). Here, a two-way, repeated-measures ANOVA (df = 29) with factors Abstraction (high/low) and Set-size (high/low) revealed a main effect of Set-size on the percentage of correct responses (accuracy; F = 9.27, p = .005), but did not reveal a significant main effect of Abstraction (F = 0.11, p = .74) or an interaction (F = 0.27, p = .61). When the same analysis was performed in the EEG data set (df = 30), we also found a main effect of Set-size on accuracy (F = 10.23, p = .003), with no significant main effect of Abstraction (F = 0.11, p = .75) nor an interaction (F = 0.05, p = .82). In the EEG data set (Figure 1G), the mean accuracy was equal to 97.72% in R4 (SD = 3.03%), 94.94% in R8 (SD = 7.43%), 97.60% in D1 (SD = 4.65%), and 94.45% in D2 (SD = 5.05%). These results show that, in each data set, the behavioral performance was matched between levels of rule abstraction, but increased set-size resulted in decreased accuracy. This allowed us to reduce the possible confounding effects of task difficulty in isolating the control processing of abstract rules. Thus, we employed the abstraction contrast to capture the neural dynamics associated with the control of rule abstraction, within the context of hierarchical control, and the set-size contrast to characterize the dynamics underlying the control of the stimulus–action association.
For the RT, in the participants who completed the fMRI session, the ANOVA revealed a main effect of Set-size (F = 273.89, p < .001), a significant main effect of Abstraction (F = 52.33, p < .001), but no significant interaction (F = 3.14, p = .087). In the fMRI data set (Figure 1F), the mean RT was equal to 890.37 msec in R4 (SD = 110.19 msec), 1111.92 msec in R8 (SD = 107.98 msec), 1003.50 msec in D1 (SD = 112.85 msec), and 1262.29 in D2 (SD = 103.67 msec). For the participants who completed the EEG experiment, the ANOVA revealed a significant main effect of Set-size on RT (F = 398.32, p < .001), as well as of Abstraction (F = 92.11, p < .001), and an interaction (F = 53.10, p < .001). In the EEG data set (Figure 1G), the mean RT was equal to 898.08 msec in R4 (SD = 111.84 msec), 1050.14 msec in R8 (SD = 98.03 msec), 962.16 msec in D1 (SD = 113.70 msec), and 1301.78 in D2 (SD = 122.54 msec).
Abstraction: Univariate fMRI and EEG Power Analyses
First, we investigated which brain areas increased in activation to the high abstraction task conditions relative to the low abstraction conditions. Univariate fMRI analysis revealed increased activations for high compared with low abstraction in LPFC (in both hemispheres), right medial portion of the superior frontal gyrus (SFGm), M1 (in both hemispheres), and right inferior parietal lobule (IPL) (Figure 2A, Table 1). The single condition contrasts versus baseline revealed that activations in LPFC and IPL were driven by the high abstraction conditions (D1 and D2; Figure 3). More specifically, although each task condition showed increased activation compared with baseline in sensorimotor-proximal areas (SMA, dorsal premotor [PMd], superior parietal lobule [SPL]), only the high abstraction conditions showed increased activation in sensorimotor-distal areas like LPFC (Figure 3B).
Figure 3.
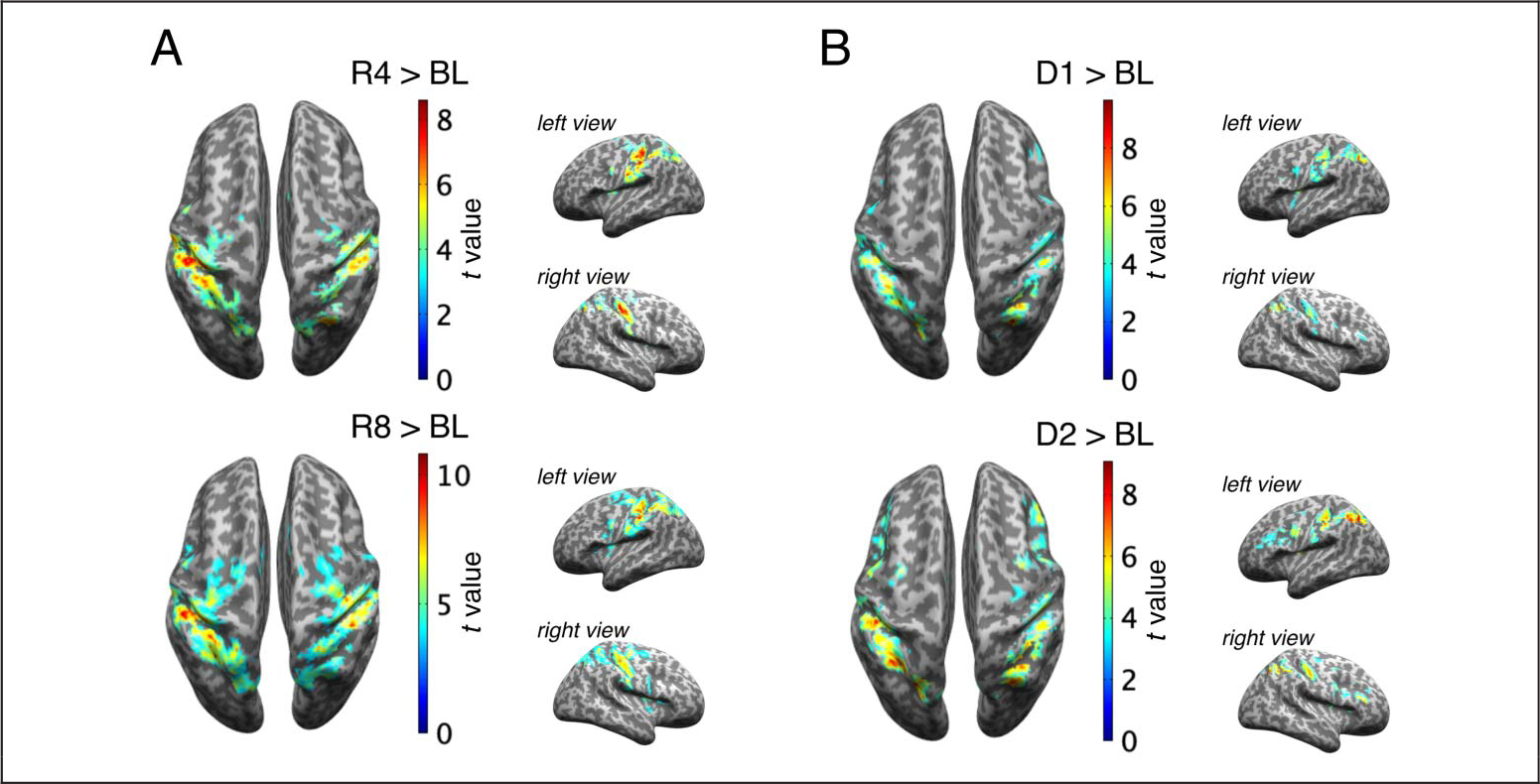
Univariate fMRI analyses for the baseline contrasts. (A–B) The results of the univariate fMRI analyses comparing each task condition to baseline (BL; pre-experiment rest period) are shown for the low-abstraction response tasks (A) and for the high abstraction dimension tasks (B).
We performed a time-varying power analysis on EEG sensor-space signals for the abstraction contrast (Figure 2B) and found a positive cluster in the observed data (higher power in high abstraction compared with low abstraction) in the delta band (~2–3 Hz) anda negative cluster (vice versa) in the alpha/beta band (~12–23 Hz). The first cluster extended approximately over frequencies 1–5 Hz and latencies 0–2000 msec (FWHM of the time-collapsed frequency distribution and of frequency-collapsed time distribution of differences 2–3 Hz and 287–1990 msec, respectively), whereas the second cluster extended approximately over 5–30 Hz and 0–2000 msec (FWHM = 8–22 Hz, 670–1601 msec). In the ranges considered, positive differences were predominantly distributed over lateral frontal and parietal electrodes at early latencies poststimulus (200–900 msec), with effect sizes peaking in the right frontal and anterior frontal electrodes (d = 0.386–0.502). At longer latencies (1000–1700 msec poststimulus), positive differences were most pronounced over the medial frontal electrodes (effect sizes ranging between d = 0.504–0.613). The scalp distribution of the negative differences was similar to the distribution of the positive differences at early latencies, with peak effect sizes in medial frontal electrodes (d = 0.405–0.418; 12–23 Hz, 600–1700 msec poststimulus). The cluster-based permutation test indicated that there was a significant difference between the high abstraction and low abstraction conditions (pperm = 0.007). These results extend to the whole scalp and replicate those obtained in our previous study, which focused on the frontal midline group of electrodes (Riddle et al., 2020).
After using IRASA to separate aperiodic (1/f) and periodic component of the power spectrum (see Methods section for more details), the estimates for the periodic components showed separability of the oscillatory peaks in the delta band (3 Hz) and theta band (6.5. Hz), in the group of medial frontal electrodes (Figure 2C). In the group of right lateral frontal electrodes instead, a theta peak was absent but the delta-band peak was still present (Figure 2C). Testing for an abstraction effect in a priori selected delta and theta frequency ranges, the cluster-based permutation test revealed a significant difference between conditions in the former (Bonferroni-adjusted pperm < 0.001), but not in the latter (Bonferroni-adjusted pperm = 0.14).
In EEG source-space (Figure 2D), we also found increased delta power for high abstraction relative to low abstraction and decreased power in the alpha/beta band. A positive cluster was found in the observed data, extending approximately over 1–5 Hz and 710–2000 msec (FWHM = 2–4 Hz, 1088–1708 msec), as well as a negative cluster that extended over frequencies and latencies in the ranges 5–40 Hz and 440–2000 msec (FWHM = 9–21 Hz, 806–1403 msec). The increase in delta power was most pronounced in seven right hemisphere cortical ROIs, including SMA (d = 0.351), IPL (d = 0.289), LPFC (d = 0.287), PMd (d = 0.235), SPL (d = 0.222), superior frontal gyrus (SFG; d = 0.207), and M1 (d = 0.186). By comparison, decreased alpha/beta power was more spread out and effect sizes peaked bilaterally in LPFC (left: d = 0.477; right: d = 0.288) and in left PMd (d = 0.309). The cluster-based permutation test revealed a significant difference between task conditions (high compared with low abstraction; pperm = 0.020).
To ensure that these effects were not driven by the back-ground electrical activity of the brain, we separated the aperiodic from periodic components of the electrical spectra using the IRASA method. We found oscillatory peaks in the delta band (~3 Hz), in the right hemisphere ROIs showing abstraction-related delta power differences (Figure 2E). In particular in LPFC, the delta-band peak was clearly distinguishable from a peak in the theta band (~6 Hz). In the observed data in the late interval (Figure 2E), an increase in periodic delta power with abstraction was most prominent in the right hemisphere, over SMA (d = 0.419), LPFC (d = 0.398), IPL (d = 0.368), PMd (d = 0.336), M1 (d = 0.333), SFG (d = 0.219), and PMd in the left hemisphere (d = 0.132). After selecting a priori frequency ranges in our data, the cluster-based permutation test revealed a significant difference between high abstraction and low abstraction conditions in the delta (Bonferroni-adjusted pperm = 0.001) but not in the theta band (Bonferroni-adjusted pperm = 0.63). No significant differences were found in the early (Bonferroni-adjusted pperm = 0.28) and response-locked intervals (Bonferroni-adjusted pperm = 0.30), in either frequency band.
Abstraction: Connectivity Analyses
Because we found distinctively stronger delta synchronization with increased abstraction, we investigated the delta- and-directed functional connectivity in the source-space ROIs of the EEG data, as a function of the level of abstraction. The results of this EEG connectivity analysis showed significant positive differences between high and low abstraction, in both the early and late stimulus-locked time intervals, but not in the response-locked interval. In the early interval, the results showed increased in-degree for high abstraction compared with low abstraction, in M1 (d = 0.367) and IPL (d = 0.408); the post hoc analysis revealed that these effects were driven by higher connectivity in high compared with low abstraction in the directed connections from LPFC to M1 (d = 0.367), and M1 to IPL (d = 0.527; Figure 4A). In the late interval, the results showed increased out-degree for high compared with low abstraction in LPFC (d = 0.351), and increased in-degree in IPL (d = 0.480) and PMd (d = 0.281); these effects were driven by the directed connections from LPFC to IPL (d = 0.335), SFGm to IPL (d = 0.524), and SPL to PMd (d = 0.406; Figure 4A).
Figure 4.
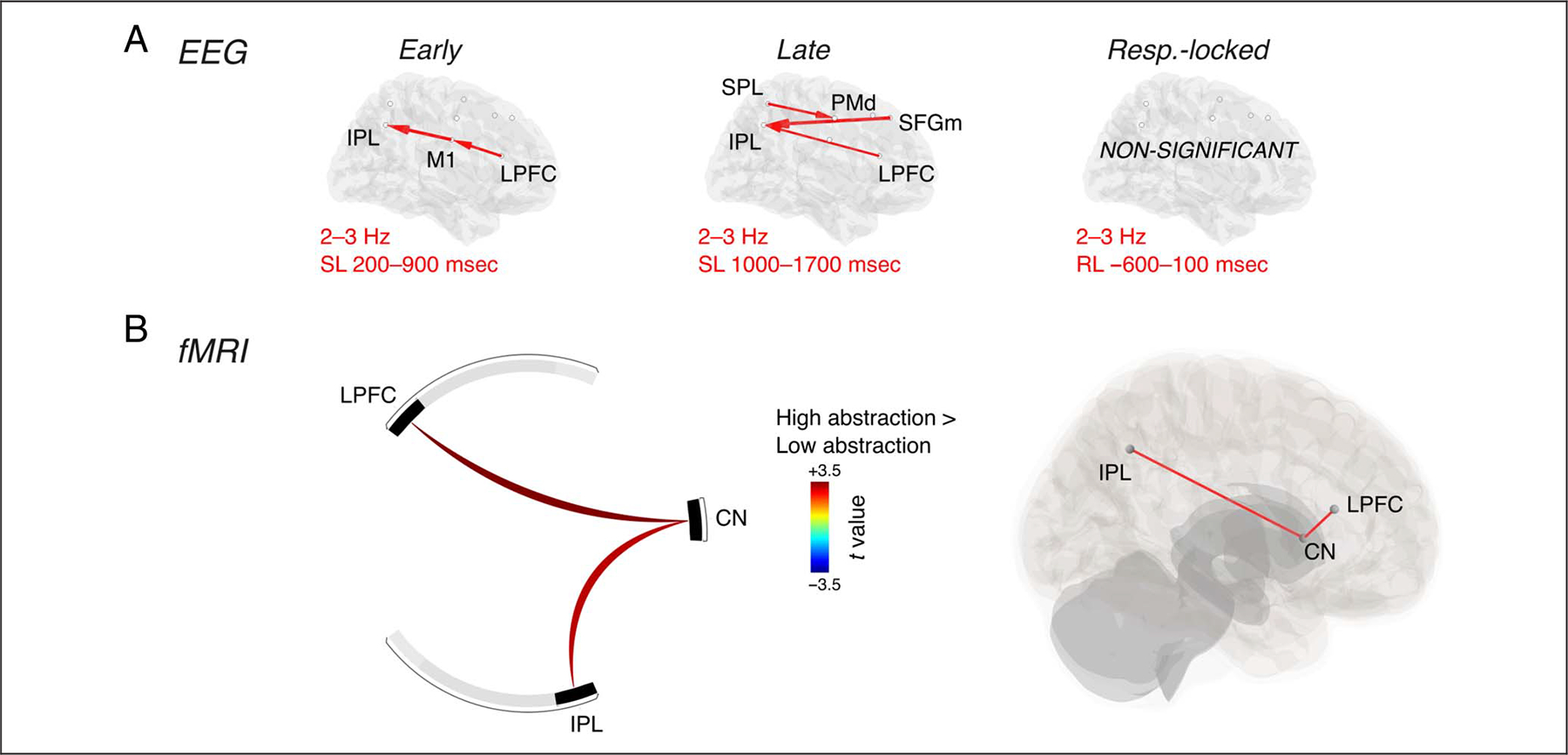
Connectivity analyses for the abstraction contrast. (A) Results of the nonparametric Granger–Geweke causality analysis for early interval (stimulus-locked: SL), late interval (stimulus-locked: SL), and response interval (response-locked: RL). (B) Results of the gPPI analysis comparing high abstraction and low abstraction.
We also conducted an analysis of fMRI connectivity for the abstraction contrast. The spatial resolution of fMRI allowed us to investigate whether subcortical regions in the dorsal striatum or THA contributed to task-driven changes in functional connectivity. We found increased functional connectivity with task abstraction between the CN and two cortical regions, LPFC (puncorr = 0.019) and IPL (puncorr = 0.032; Figure 4B).
Set-size: Univariate fMRI and EEG Power Analyses
Next, we investigated which regions were activated for task conditions with a high set-size versus a low set-size. Univariate fMRI analysis revealed increased activations for high compared with low set-size in right LPFC, SMA, PMd (in both hemispheres), and SPL (Figure 5A, Table 1). The results of the univariate fMRI analyses comparing each task condition to baseline showed significant activation in PMd, SMA, and SPL, for every task condition (Figure 3).
In a time-varying, stimulus-locked power analysis on EEG sensor-space signals (Figure 5B), we found increased power with set-size in the theta band, predominantly in frontal midline electrodes (peak effect size in FCz: d = 0.375). Here, a positive cluster extended approximately over frequencies 2–7 Hz and latencies 110–2000 msec (FWHM = 3–6 Hz, 815–1550 msec). The results further showed decreased power with set-size in the alpha/beta band, with a negative cluster found in the observed data (7–30 Hz, 225–2000 msec; FWHM = 9–18 Hz, 600–1480 msec), most pronounced in central and parietal electrodes, bilaterally (peak effect size in C3: d = 0.309). Similar patterns were obtained from the response-locked analysis (Figure 5C). Here, a positive cluster in the observed data was found in the theta band (1–8 Hz, −2000–1000 msec; FWHM = 2–5 Hz, −1525 to −742 msec) and a negative cluster in the alpha band (5–37 Hz, −1360–1000 msec; FWHM = 9–13 Hz, −987 to −496 msec). In these ranges, power differences were most pronounced in medial frontal (peak effect size in FCz: d = 0.426) and posterior parietal electrodes (peak effect size in P4: d = 0.379), respectively. Cluster-based permutation tests revealed a significant difference between high set-size and low set-size conditions, in both stimulus-locked (pperm = 0.020) and response-locked analysis (pperm = 0.013).
IRASA demonstrated that the periodic oscillatory component in the theta band (peak at 6.5 Hz) is separable from delta band oscillatory peak (3 Hz) in the group of medial frontal electrodes, and demonstrated the presence of alpha-band oscillatory components (peak at 10 Hz) in central-parietal electrodes (Figure 5D). Testing for an effect in a priori selected delta and theta frequency ranges, cluster-based permutation tests identified that there was a significant difference between high set-size and low set-size only in the theta band (Bonferroni-adjusted pperm = 0.002) and not in the delta band (Bonferroni-adjusted pperm = 0.17).
In EEG source-space, the stimulus-locked analysis confirmed the patterns found in sensor-space. We found decreased power with set-size in the alpha/beta-band (negative cluster in the observed data, extending over frequencies 7–34 Hz and latencies 440–2000 msec; FWHM = 9–21 Hz, 805–1400 msec), over a distributed group of ROIs (Figure 5E). Between-conditions differences were most pronounced in the alpha-band (8–13 Hz, 600–1700 msec poststimulus), in PMd (d = 0.527), SMA (d = 0.406), IPL (d = 0.405), and SPL (d = 0.360) in the right hemisphere. We also observed a trend toward theta band power increase with increased set-size in medial frontal regions, in particular SMA, with a positive cluster extending over 3–7 Hz and 830–2000 msec (FWHM = 4–6 Hz, 980–1610 msec). The cluster-based permutation test indicated that there was a significant difference between high and low set-size (pperm = 0.020).
When we separated the periodic component of the theta band from the aperiodic background activity of the brain using IRASA (Figure 5F), we identified separable peaks in the delta (~3 Hz) and theta (~6 Hz) band. For the power spectrum periodic components, in the late interval, an increase in theta power with set-size was most prominent in SMA (d = 0.589), SFG (d = 0.317), and PMd (d = 0.275) in the right hemisphere, whereas in the response-locked interval, the power increase was most pronounced in the right hemisphere in LPFC (d = 0.485), PMd (d = 0.362), SMA (d = 0.266), SFGm (d = 0.225), and SFG (d = 0.145), and in the left hemisphere in PMd (d = 0.496), LPFC (d = 0.387), and M1 (d = 0.218). In each latency interval, the cluster-based permutation tests revealed a significant difference between task conditions in the theta frequency range (Bonferroni-adjusted pperm < 0.001 and pperm = 0.001, respectively, in the late and response-locked interval). We did not find any significant differences in the delta range (Bonferroni-adjusted pperm = 0.16 in the late interval; Bonferroni-adjusted pperm = 1.0 in the response-locked interval).
Set-size: Connectivity Analyses
With increasing set-size, we found stronger synchronization in the theta rather than the delta band. Thus, we investigated the changes in theta-band directed functional connectivity in source-space EEG, driven by increased set-size. This analysis revealed a significant increase in theta-band connectivity as a function of the set-size, in all three time intervals analyzed. In the early interval, the results showed increased out-degree for high compared with low set-size in SFGm (d = 0.578); a post hoc analysis revealed that this effect was driven by increased connectivity with set-size in the directed connections from SFGm to LPFC (d = 0.379) and PMd (d = 0.400; Figure 6A). In the late interval, we found increased out-degree with set-size in SFGm (d = 0.453), and increased in-degree in LPFC (d = 0.376), PMd (d = 0.517), and SPL (d = 0.474); these effects were driven by increased theta connectivity with set-size in the connections from SFGm to LPFC (d = 0.458) and PMd (d = 0.775), SMA to PMd (d = 0.330), LPFC to SPL (d = 0.550), and SFG to SPL (d = 0.630; Figure 6A). In the response-locked interval, we found that out-degree was higher for high set-size than low set-size in LPFC (d = 0.364), whereas in-degree was higher in PMd (d = 0.546); the post hoc comparison showed increased theta connectivity with set-size in the connections from LPFC to SPL (d = 0.513) and M1 (d = 0.544; Figure 6A).
Figure 6.
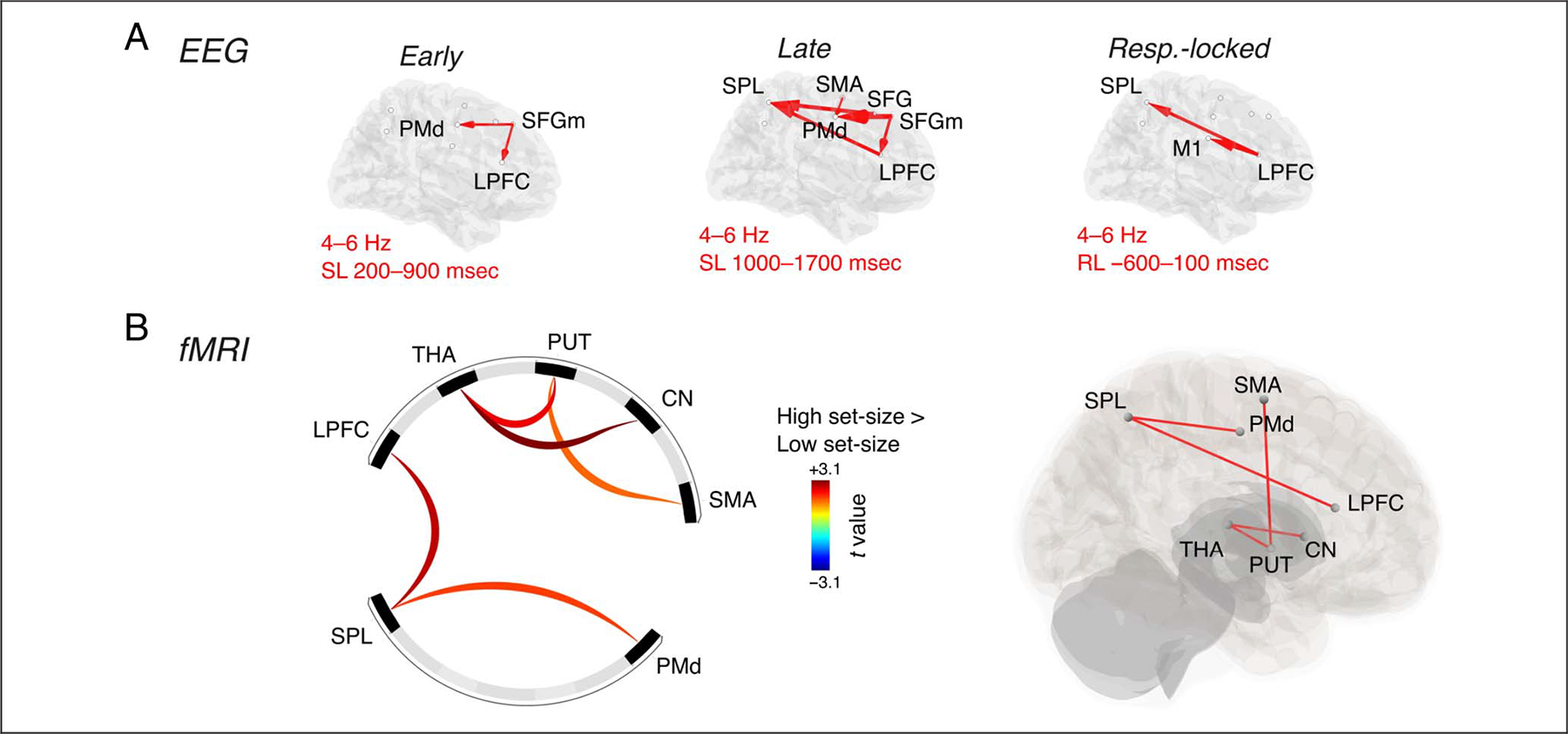
Connectivity analyses for the set-size contrast. (A) Results of the nonparametric Granger–Geweke causality analysis for early interval (stimulus-locked: SL), late interval (stimulus-locked: SL), and response interval (response-locked: RL). (B) Results of the gPPI analysis comparing high set-size and low set-size.
We further performed a connectivity analysis of the fMRI data for the set-size contrast. This analysis revealed increased functional connectivity with set-size between PMd–SPL (puncorr = 0.032) and LPFC–SPL (puncorr = 0.006), and in the connections between SMA–PUT (puncorr = 0.040), PUT–THA (puncorr = 0.042), and CN–THA (puncorr = 0.040; Figure 6B).
Response-locked Power Analyses
Although our hypothesis focused on the role of low-frequency neural oscillations in the delta and theta bands to coordinate large-scale network activity, our analyses assessed a broader range of frequencies up to 50 Hz, and we also found power modulations in the alpha/beta band for both the abstraction and set-size contrasts. We used response-locked analyses to further investigate whether these modulations coincided with the same regions exhibiting modulations in the delta and theta bands. For the abstraction contrast, the power analyses were repeated using the response-locked epochs (−2000 to 1000 msec). The results of these response-locked analyses, both in sensor-space and source-space, confirmed that alpha/beta power is reduced with abstraction (Figure 7). In the observed data in sensor-space, a negative cluster extended approximately over frequencies 5–25 Hz and latencies −1350 to 1000 msec (FWHM = 7–17 Hz, −287 to 210 msec). In source-space, a negative cluster was found in our data, extending over 6–29 Hz and − 850 to 582 msec (FWHM = 11–18 Hz, −557 to 144 msec). Here, the decrease in power was most pronounced at ~15 Hz, in LPFC bilaterally (left: d = 0.402; right: d = 0.342). The cluster-based permutation tests identified that there was a significant difference between high and low abstraction, in both sensor-space (pperm = 0.039) and source-space (pperm = 0.013). These results suggest that the previously observed beta-band power effects (Figure 2B–D) are not simply driven by timing differences in the motor-related processes between conditions, because of differences in RT; rather, the beta-band effects are specifically associated with the control of rule abstraction, with high abstraction conditions showing stronger beta-band desynchronization, predominantly in lateral areas.
In the response-locked interval, the source-space results revealed specifically stronger alpha-band (as opposed to beta-band) desynchronization with increased set-size (Figure 8), in line with the sensor-space results (Figure 5C). A negative cluster in the observed data extended from approximately 5 to 38 Hz, over latencies between −1245 and 1000 msec (FWHM = 8–17 Hz, −1044 to −411 msec). The decrease in power was most prominent at ~11 Hz, in the right hemisphere in PMd (d = 0.482), SPL (d = 0.353), and LPFC (d = 0.345), and in the left hemisphere in SPL (d = 0.365), M1 (d = 0.314), and LPFC (d = 0.306). The cluster-based per-mutation test revealed a significant difference between high set-size and low set-size conditions (pperm = 0.007). Together, the results of the response-locked analyses suggest that the observed alpha/beta-band desynchronization effects, both abstraction-dependent and set-size-dependent, do not simply reflect motor preparation because of the difference in RTs between task conditions, but rather they may have a specific role for each level of control.
DISCUSSION
In this study, we analyzed an fMRI and EEG data set with the same task to characterize the neural dynamics of control signals that underlie different components of hierarchical cognitive control. Our results show that distinct neural oscillations underlie the inter-areal synchronization within distributed functional networks, to support two distinct levels of processing of cognitive control, one related to the control of rule abstraction and the other to the control of stimulus–action associations. A frontal–parietal synchronization between LPFC and IPL underlies the control of the relevant abstract rule via top–down delta oscillations (~2–3 Hz). By comparison, theta oscillations (~4–7 Hz) act as control signals for the integration of information relative to stimulus–action associations, in more caudal and midline regions of the frontal cortex. This level of control unfolds slightly later in time, with more prominent response-locked dynamics, whereas the control of rule abstraction was most prominent in stimulus-locked dynamics. These findings support a model of dynamic cognitive control processing via multiplexed synchronization mechanisms.
The neural dynamics of hierarchical cognitive control were first tested in four participants undergoing intracranial electrocorticography monitoring for epileptic seizures (Voytek et al., 2015) using response and dimension tasks similar to the ones used here (Badre & D’Esposito, 2007, 2009; Badre, 2008). This seminal intracranial work provided evidence that pFC exerts greater influence on the processing in primary motor and premotor cortices (M1), than vice versa, through control signals in the theta band (4–8 Hz; Voytek et al., 2015). However, in this study, behavioral performance was not matched between the two tasks, which could introduce possible confounding effects of task difficulty in isolating the control processing of abstract rules. Here and in previous work, we matched participants’ performance across levels of rule abstraction (Riddle, McFerren, & Frohlich, 2021; Riddle et al., 2020), which allowed us to dissociate delta and theta oscillations in the frontal areas involved in hierarchical cognitive control. We further demonstrated that each rhythm is associated with a specific level of control processing. These findings support a model by which there is a separation of signals within frontoparietal networks for different levels of hierarchical control, via “frequency-division multiplexing” between delta and theta oscillations. This multiplexing scheme, implemented by segregating the signals by frequency bands of oscillations, makes it possible for neural activity to carry multiple independently accessible information channels (Akam & Kullmann, 2014), which allows for multiple levels of hierarchical cognitive control to be processed in parallel, rather than in a strictly serial fashion. Our results demonstrate that the two levels of control processing we studied are characterized by overlapping temporal dynamics, which is consistent with previous behavioral results, where participants tend to exhibit parallel (rather than serial) decision-making dynamics in tasks with hierarchically structured rules (Ranti, Chatham, & Badre, 2015). Such parallel processing through delta and theta neural oscillations may provide a time-efficient way to perform complex tasks.
Other studies have advanced the hypothesis that theta oscillations, specifically, support the implementation of cognitive control (Cooper et al., 2019; Sauseng et al., 2019; Cavanagh & Frank, 2014; Cohen & Donner, 2013). Furthermore, theta oscillations might adaptively change (or “shift”) their peak frequency within the ~4–7 Hz range, depending on task demands. A recent study has provided supporting evidence for this adaptive mechanism using behavioral and EEG data with a computational modeling approach (Senoussi et al., 2022). By manipulating task difficulty, Senoussi and colleagues showed that theta-band oscillations over middle frontal gyrus change their peak frequency according to task demands, with difficult tasks showing a lower peak frequency in the theta band compared with easy tasks. A computational model, in which an MFC unit generated theta oscillations that orchestrated biased competition between rule nodes in a LPFC unit, achieved optimal accuracy at a slower theta frequency (lower peak frequency) for difficult rules, whereas a faster theta (higher peak frequency) was optimal for easier rules. Based on these findings, it was proposed that more abstract task rules (known to recruit more rostral areas) could elicit a slowing of the neural oscillations generated by MFC even toward the delta range (Senoussi et al., 2022). Our current findings suggest, instead, that a frontoparietal control system operates through multiplexed neural processes, leveraging distinct neural oscillations for large-scale synchronization, which is not consistent with the existence of a (simply) unitary, adaptive control system in middle frontal gyrus. Although we did not observe any shifts in leading frequencies across task conditions, our results do not entirely exclude the possibility that there might also be shifts in the leading frequency of theta oscillations. If a frequency shift were to occur, we speculate that it would take place within the level of control for stimulus–action associations, in the theta band (~4–7 Hz). Furthermore, our findings are in line with the predictions of the model by Senoussi and colleagues, in that theta-mediated interactions from MFC to LPFC orchestrate the competition between task rules (Senoussi et al., 2022), for which our results of increased theta band directed connectivity from medial frontal areas to LPFC in the control of stimulus–action associations provide supporting evidence.
We also found that, in addition to low-frequency synchronization in the delta/theta band, higher levels of control processing are associated with stronger desynchronization of alpha/beta oscillations (~8–23 Hz). This desynchronization peaked in the beta band for the abstraction contrast and in the alpha band for the set-size contrast. We previously observed that different motifs of cross-frequency coupling underlie the two components of cognitive control, in the form of coupling between the phase of slow oscillations and the amplitude of higher frequency oscillations (phase-amplitude coupling [PAC]; Canolty & Knight, 2010). Specifically, we found increased delta–beta PAC during high abstraction and high set-size and increased theta–gamma PAC during low abstraction conditions (Riddle et al., 2020). Furthermore, using transcranial alternating current stimulation in healthy individuals, we found causal evidence that distinct cross-frequency coupling motifs underlie these two components of control (Riddle et al., 2021). In the current study, we did not explicitly investigate cross-frequency coupling mechanisms with gamma oscillations, because of the intrinsic limitations of noninvasive EEG in examining source-localized, high-frequency activity. Nonetheless, based on these previous findings and the current results, it is possible to distinguish two main groups of neural rhythms, one including delta–beta oscillations and the other including theta–alpha (–gamma) oscillations, each specifically associated either with the control of rule abstraction (predominantly in lateral areas) or the control of stimulus–action associations (predominantly in dorsal midline areas). We speculate that the mid-frequency, beta, and alpha oscillations serve as inhibitory control signals for maintaining task-relevant representations. Working memory studies, for example, indicate that there is an interplay between gamma and beta in pFC (Lundqvist et al., 2016, 2023), whereas alpha dynamics are typically observed during working memory maintenance in parietal and visual cortices (Sreenivasan & D’Esposito, 2019; van Ede, 2018; Klimesch, 2012). Beta and alpha oscillations may thus accomplish the control of stored representations, separately for abstract rules and for stimulus information. Conversely, the desynchronization of alpha/beta oscillations may reflect a mechanism of disinhibition from these inhibitory control signals, which allows reading out relevant information from working memory (Buschman & Miller, 2022; Miller, Lundqvist, & Bastos, 2018).
We showed that delta and theta oscillations are engaged in two distributed association networks to support different levels of control processing. This idea that there are multiple, distributed association networks is supported by observations in monkey studies demonstrating parallel anatomical projections between sensory association areas and pFC (Goldman-Rakic, 1988), as well as by rest and task-based fMRI studies in humans (Nee, 2021; Choi et al., 2018; Braga & Buckner, 2017; Farooqui, Mitchell, Thompson, & Duncan, 2012; Yeo et al., 2011). These distributed association networks include both corticocortical and corticostriatal connections (Haber, 2003). Our results suggest that the control of rule abstraction is associated with an increase in the functional connectivity of two cortical regions, LPFC and IPL, with the caudate nucleus in the dorsal striatum, which is part of the basal ganglia (BG). This is in line with previous studies indicating that the rostral dorsal caudate serves as a connector hub for IPL and pFC projections, whereas only smaller projection patches are observed in the putamen (Choi et al., 2018; Choi, Tanimura, Vage, Yates, & Haber, 2017). In contrast, the posterior and dorsolateral anterior putamen receives projections predominantly from the primary motor and supplementary motor cortices (Choi, Yeo, & Buckner, 2012; Draganski et al., 2008). Although we found that increased functional connectivity between the supplementary motor cortex and putamen, as well as within BG–thalamus connections, underlies the control of stimulus–action associations, we did not find significant effects on any of the thalamocortical connections with either the abstraction or set-size manipulation. However, thalamocortical projections are known to link the cortico–subcortical circuits with the BG back to the cortex, creating cortical–BG–thalamocortical loops (Hwang & D’Esposito, 2022; Haber, Adler, & Bergman, 2012). These parallel loops through the thalamus may update in working memory the different contextual representations (Badre & Frank, 2012; Frank & Badre, 2012), as well as enhance functional cortical connectivity and support the distinct corticocortical synchronization mechanisms that we outlined here for the different levels of hierarchical control processing (Shine et al., 2023; Schmitt et al., 2017). Future work could attempt to dissociate the two cortical–subcortical loops hypothesized to underlie the control of rule abstraction and stimulus–action associations, by using TMS, as previous work demonstrated that at rest targeting rostral regions spreads activation to the caudate nucleus whereas stimulation of caudal frontal cortex activates the putamen (Riddle et al., 2022).
Our results contribute to previous work on hierarchical cognitive control, by characterizing the neural dynamics of distinct cognitive control signals and showing that, although there is a significant overlap in time between the dynamics of the two control processes, the control of rule abstraction (delta oscillations-mediated) appears to slightly precede the control of stimulus–action associations (theta oscillations-mediated). The observed separability of these control signals is in line with the predictions of the “cascade model” of cognitive control, in that separable top–down control signals resolve the competition among alternative action representations, at different levels of the rostro–caudal axis of pFC (Koechlin & Summerfield, 2007; Koechlin et al., 2003). A central prediction of the cascade model is that control signals integrate information from superordinate to subordinate levels, progressing from sensorimotor-distal to sensorimotor-proximal areas, that is, from farthest to nearest to the sensory-motor cortex. Revising this model, recent findings suggest that, although there exists an axis of functional differentiation in pFC, the most rostral part of pFC (sensorimotor-distal) is likely not to be the apex of the hierarchy of control processing; rather, an adaptive nexus for the functional integration of information seems situated in areas in the middle of the LPFC (Pitts & Nee, 2022; Nee, 2021). We showed within both control levels significant modulations of the functional connections through the “LPFC” ROI, which worked primarily as functional sender in the control of rule abstraction and as functional receiver in the control of stimulus–action associations; however, we did not provide any direct evidence of whether this area, which sits in the mid-portion of pFC, works as an integrative hub. Furthermore, we only assessed two levels of cognitive control processing, which correspond to the levels of “sensorimotor control” (associating stimuli to appropriate actions) and “contextual control” (stimulus–action associations dependence on environmental context) in hierarchical control experiments (Badre & Nee, 2018), but other levels of control have been proposed, see Pitts and Nee (2022), Nee (2021), Nee and D’Esposito (2016, 2017). Future work should consider these further levels to expand the findings presented in this study.
Funding Information
This work was supported by the Swiss National Science Foundation (https://dx.doi.org/10.13039/501100001711), grant numbers: 195083 and 214404 to M. F. P.; and the National Institutes of Health (https://dx.doi.org/10.13039/100000002), grant number: R01MH063901 to M. D., and grant number: K99/R00MH126161 to J. R.
Footnotes
Diversity in Citation Practices
Retrospective analysis of the citations in every article published in this journal from 2010 to 2021 reveals a persistent pattern of gender imbalance: Although the proportions of authorship teams (categorized by estimated gender identification of first author/last author) publishing in the Journal of Cognitive Neuroscience (JoCN) during this period were M(an)/M = .407, W(oman)/M = .32, M/W = .115, and W/W = .159, the comparable proportions for the articles that these authorship teams cited were M/M = .549, W/M = .257, M/W = .109, and W/W = .085 (Postle and Fulvio, JoCN, 34:1, pp. 1–3). Consequently, JoCN encourages all authors to consider gender balance explicitly when selecting which articles to cite and gives them the opportunity to report their article’s gender citation balance.
Data Availability Statement
Analysis scripts, behavioral data, preprocessed EEG data, and results of the group-level fMRI analyses are available on the Open Science Framework (https://osf.io/5vs2x/). Supplemental data and supporting files are available upon request via email to the lead author.
REFERENCES
- Akam T, & Kullmann DM (2014). Oscillatory multiplexing of population codes for selective communication in the mammalian brain. Nature Reviews Neuroscience, 15, 111–122. 10.1038/nrn3668, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badre D (2008). Cognitive control, hierarchy, and the rostro-caudal organization of the frontal lobes. Trends in Cognitive Sciences, 12, 193–200. 10.1016/j.tics.2008.02.004, [DOI] [PubMed] [Google Scholar]
- Badre D, & D’Esposito M (2007). Functional magnetic resonance imaging evidence for a hierarchical organization of the prefrontal cortex. Journal of Cognitive Neuroscience, 19, 2082–2099. 10.1162/jocn.2007.19.12.2082, [DOI] [PubMed] [Google Scholar]
- Badre D, & D’Esposito M (2009). Is the rostro-caudal axis of the frontal lobe hierarchical? Nature Reviews Neuroscience, 10, 659–669. 10.1038/nrn2667, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badre D, & Frank MJ (2012). Mechanisms of hierarchical reinforcement learning in cortico-striatal circuits 2: Evidence from fMRI. Cerebral Cortex, 22, 527–536. 10.1093/cercor/bhr117, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badre D, & Nee DE (2018). Frontal cortex and the hierarchical control of behavior. Trends in Cognitive Sciences, 22, 170–188. 10.1016/j.tics.2017.11.005, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braga RM, & Buckner RL (2017). Parallel interdigitated distributed networks within the individual estimated by intrinsic functional connectivity. Neuron, 95, 457–471. 10.1016/j.neuron.2017.06.038, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breska A, & Deouell LY (2017). Neural mechanisms of rhythm-based temporal prediction: Delta phase-locking reflects temporal predictability but not rhythmic entrainment. PLoS Biology, 15, e2001665. 10.1371/journal.pbio.2001665, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunge SA (2004). How we use rules to select actions: A review of evidence from cognitive neuroscience. Cognitive, Affective, & Behavioral Neuroscience, 4, 564–579. 10.3758/CABN.4.4.564, [DOI] [PubMed] [Google Scholar]
- Buschman TJ, & Miller EK (2022). Working memory is complex and dynamic, like your thoughts. Journal of Cognitive Neuroscience, 35, 17–23. 10.1162/jocn_a_01940, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G (2006). Rhythms of the brain. Oxford University Press. 10.1093/acprof:oso/9780195301069.001.0001 [DOI] [Google Scholar]
- Buzsáki G, & Draguhn A (2004). Neuronal oscillations in cortical networks. Science, 304, 1926–1929. 10.1126/science.1099745, [DOI] [PubMed] [Google Scholar]
- Canolty RT, & Knight RT (2010). The functional role of cross-frequency coupling. Trends in Cognitive Sciences, 14, 506–515. 10.1016/j.tics.2010.09.001, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanagh JF, & Frank MJ (2014). Frontal theta as a mechanism for cognitive control. Trends in Cognitive Sciences, 18, 414–421. 10.1016/j.tics.2014.04.012, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cellier D, Petersen IT, & Hwang K (2022). Dynamics of hierarchical task representations. Journal of Neuroscience, 42, 7276–7284. 10.1523/JNEUROSCI.0233-22.2022, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi EY, Drayna GK, & Badre D (2018). Evidence for a functional hierarchy of association networks. Journal of Cognitive Neuroscience, 30, 722–736. 10.1162/jocn_a_01229, [DOI] [PubMed] [Google Scholar]
- Choi EY, Tanimura Y, Vage PR, Yates EH, & Haber SN (2017). Convergence of prefrontal and parietal anatomical projections in a connectional hub in the striatum. Neuroimage, 146, 821–832. 10.1016/j.neuroimage.2016.09.037, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi EY, Yeo BTT, & Buckner RL (2012). The organization of the human striatum estimated by intrinsic functional connectivity. Journal of Neurophysiology, 108, 2242–2263. 10.1152/jn.00270.2012, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J (1992). A power primer. Psychological Bulletin, 112, 155–159. 10.1037/0033-2909.112.1.155, [DOI] [PubMed] [Google Scholar]
- Cohen MX, & Donner TH (2013). Midfrontal conflict-related theta-band power reflects neural oscillations that predict behavior. Journal of Neurophysiology, 110, 2752–2763. 10.1152/jn.00479.2013, [DOI] [PubMed] [Google Scholar]
- Cooper PS, Karayanidis F, McKewen M, McLellan-Hall S, Wong ASW, Skippen P, et al. (2019). Frontal theta predicts specific cognitive control-induced behavioural changes beyond general reaction time slowing. Neuroimage, 189, 130–140. 10.1016/j.neuroimage.2019.01.022, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtis CE, & D’Esposito M (2003). Persistent activity in the prefrontal cortex during working memory. Trends in Cognitive Sciences, 7, 415–423. 10.1016/S1364-6613(03)00197-9, [DOI] [PubMed] [Google Scholar]
- D’Esposito M, & Postle BR (2015). The cognitive neuroscience of working memory. Annual Review of Psychology, 66, 115–142. 10.1146/annurev-psych-010814-015031, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A, & Makeig S (2004). EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. Journal of Neuroscience Methods, 134, 9–21. 10.1016/j.jneumeth.2003.10.009, [DOI] [PubMed] [Google Scholar]
- de Vries IEJ, van Driel J, Karacaoglu M, & Olivers CNL (2018). Priority switches in visual working memory are supported by frontal delta and posterior alpha interactions. Cerebral Cortex, 28, 4090–4104. 10.1093/cercor/bhy223, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhamala M, Rangarajan G, & Ding M (2008a). Analyzing information flow in brain networks with nonparametric Granger causality. Neuroimage, 41, 354–362. 10.1016/j.neuroimage.2008.02.020, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhamala M, Rangarajan G, & Ding M (2008b). Estimating granger causality from Fourier and wavelet transforms of time series data. Physical Review Letters, 100, 018701. 10.1103/PhysRevLett.100.018701, [DOI] [PubMed] [Google Scholar]
- Draganski B, Kherif F, Klöppel S, Cook PA, Alexander DC, Parker GJM, et al. (2008). Evidence for segregated and integrative connectivity patterns in the human basal ganglia. Journal of Neuroscience, 28, 7143–7152. 10.1523/JNEUROSCI.1486-08.2008, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farooqui AA, Mitchell D, Thompson R, & Duncan J (2012). Hierarchical organization of cognition reflected in distributed frontoparietal activity. Journal of Neuroscience, 32, 17373–17381. 10.1523/JNEUROSCI.0598-12.2012, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Formica S, González-García C, Senoussi M, & Brass M (2021). Neural oscillations track the maintenance and proceduralization of novel instructions. Neuroimage, 232, 117870. 10.1016/j.neuroimage.2021.117870, [DOI] [PubMed] [Google Scholar]
- Frank MJ, & Badre D (2012). Mechanisms of hierarchical reinforcement learning in corticostriatal circuits 1: Computational analysis. Cerebral Cortex, 22, 509–526. 10.1093/cercor/bhr114, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Holmes AP, Worsley KJ, Poline J-P, Frith CD, & Frackowiak RSJ (1994). Statistical parametric maps in functional imaging: A general linear approach. Human Brain Mapping, 2, 189–210. 10.1002/hbm.460020402 [DOI] [Google Scholar]
- Fuster JM (2001). The prefrontal cortex–an update: Time is of the essence. Neuron, 30, 319–333. 10.1016/S0896-6273(01)00285-9, [DOI] [PubMed] [Google Scholar]
- Geweke J (1982). Measurement of linear dependence and feedback between multiple time series. Journal of the American Statistical Association, 77, 304–313. 10.1080/01621459.1982.10477803 [DOI] [Google Scholar]
- Goldman-Rakic PS (1988). Topography of cognition: Parallel distributed networks in primate association cortex. Annual Review of Neuroscience, 11, 137–156. 10.1146/annurev.ne.11.030188.001033, [DOI] [PubMed] [Google Scholar]
- Grinband J, Wager TD, Lindquist M, Ferrera VP, & Hirsch J (2008). Detection of time-varying signals in event-related fMRI designs. Neuroimage, 43, 509–520. 10.1016/j.neuroimage.2008.07.065, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haber SN (2003). The primate basal ganglia: Parallel and integrative networks. Journal of Chemical Neuroanatomy, 26, 317–330. 10.1016/j.jchemneu.2003.10.003, [DOI] [PubMed] [Google Scholar]
- Haber SN, Adler A, & Bergman H (2012). The basal ganglia. In The human nervous system (pp. 678–738). Elsevier. 10.1016/B978-0-12-374236-0.10020-3 [DOI] [Google Scholar]
- Helfrich RF, Breska A, & Knight RT (2019). Neural entrainment and network resonance in support of top–down guided attention. Current Opinion in Psychology, 29, 82–89. 10.1016/j.copsyc.2018.12.016, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helfrich RF, & Knight RT (2016). Oscillatory dynamics of prefrontal cognitive control. Trends in Cognitive Sciences, 20, 916–930. 10.1016/j.tics.2016.09.007, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang K, & D’Esposito M (2022). The thalamus in cognitive control. In Halassa MM (Ed.), The thalamus (pp. 307–323). Cambridge University Press. 10.1017/9781108674287.017 [DOI] [Google Scholar]
- Klimesch W (2012). α-band oscillations, attention, and controlled access to stored information. Trends in Cognitive Sciences, 16, 606–617. 10.1016/j.tics.2012.10.007, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koechlin E, Ody C, & Kouneiher F (2003). The architecture of cognitive control in the human prefrontal cortex. Science, 302, 1181–1185. 10.1126/science.1088545, [DOI] [PubMed] [Google Scholar]
- Koechlin E, & Summerfield C (2007). An information theoretical approach to prefrontal executive function. Trends in Cognitive Sciences, 11, 229–235. 10.1016/j.tics.2007.04.005, [DOI] [PubMed] [Google Scholar]
- Lorenc ES, & Sreenivasan KK (2021). Reframing the debate: The distributed systems view of working memory. Visual Cognition, 29, 416–424. 10.1080/13506285.2021.1899091 [DOI] [Google Scholar]
- Lundqvist M, Brincat SL, Rose J, Warden MR, Buschman TJ, Miller EK, et al. (2023). Working memory control dynamics follow principles of spatial computing. Nature Communications, 14, 1429. 10.1038/s41467-023-36555-4, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lundqvist M, Rose J, Herman P, Brincat SL, Buschman TJ, & Miller EK (2016). Gamma and beta bursts underlie working memory. Neuron, 90, 152–164. 10.1016/j.neuron.2016.02.028, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maris E, & Oostenveld R (2007). Nonparametric statistical testing of EEG- and MEG-data. Journal of Neuroscience Methods, 164, 177–190. 10.1016/j.jneumeth.2007.03.024, [DOI] [PubMed] [Google Scholar]
- McLaren DG, Ries ML, Xu G, & Johnson SC (2012). A generalized form of context-dependent psychophysiological interactions (gPPI): A comparison to standard approaches. Neuroimage, 61, 1277–1286. 10.1016/j.neuroimage.2012.03.068, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon V, & D’Esposito M (2022). The role of PFC networks in cognitive control and executive function. Neuropsychopharmacology, 47, 90–103. 10.1038/s41386-021-01152-w, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK, & Cohen JD (2001). An integrative theory of prefrontal cortex function. Annual Review of Neuroscience, 24, 167–202. 10.1146/annurev.neuro.24.1.167, [DOI] [PubMed] [Google Scholar]
- Miller EK, Lundqvist M, & Bastos AM (2018). Working memory 2.0. Neuron, 100, 463–475. 10.1016/j.neuron.2018.09.023, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nee DE (2021). Integrative frontal-parietal dynamics supporting cognitive control. eLife, 10, e57244. 10.7554/eLife.57244, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nee DE, & D’Esposito M (2016). The hierarchical organization of the lateral prefrontal cortex. eLife, 5, e12112. 10.7554/eLife.12112, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nee DE, & D’Esposito M (2017). Causal evidence for lateral prefrontal cortex dynamics supporting cognitive control. eLife, 6, e28040. 10.7554/eLife.28040, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieto-Castanon A (2020). Handbook of functional connectivity magnetic resonance imaging methods in CONN. Hilbert Press. 10.56441/hilbertpress.2207.6598 [DOI] [Google Scholar]
- Oostenveld R, Fries P, Maris E, & Schoffelen J-M (2011). FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data.Computational Intelligence and Neuroscience, 2011, 156869. 10.1155/2011/156869, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagnotta MF, Dhamala M, & Plomp G (2018). Benchmarking nonparametric Granger causality: Robustness against downsampling and influence of spectral decomposition parameters. Neuroimage, 183, 478–494. 10.1016/j.neuroimage.2018.07.046, [DOI] [PubMed] [Google Scholar]
- Penny WD, Friston KJ, Ashburner JT, Kiebel SJ, & Nichols TE (2011). Statistical parametric mapping: The analysis of functional brain images. Elsevier. [Google Scholar]
- Pitts M, & Nee DE (2022). Generalizing the control architecture of the lateral prefrontal cortex. Neurobiology of Learning and Memory, 195, 107688. 10.1016/j.nlm.2022.107688, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranti C, Chatham CH, & Badre D (2015). Parallel temporal dynamics in hierarchical cognitive control. Cognition, 142, 205–229. 10.1016/j.cognition.2015.05.003, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riddle J, McFerren A, & Frohlich F (2021). Causal role of cross-frequency coupling in distinct components of cognitive control. Progress in Neurobiology, 202, 102033. 10.1016/j.pneurobio.2021.102033, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riddle J, Scimeca JM, Pagnotta MF, Inglis B, Sheltraw D, Muse-Fisher C, et al. (2022). A guide for concurrent TMS-fMRI to investigate functional brain networks. Frontiers in Human Neuroscience, 16, 1050605. 10.3389/fnhum.2022.1050605, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riddle J, Vogelsang DA, Hwang K, Cellier D, & D’Esposito M (2020). Distinct oscillatory dynamics underlie different components of hierarchical cognitive control. Journal of Neuroscience, 40, 4945–4953. 10.1523/JNEUROSCI.0617-20.2020, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubega M, Carboni M, Seeber M, Pascucci D, Tourbier S, Toscano G, et al. (2019). Estimating EEG source dipole orientation based on singular-value decomposition for connectivity analysis. Brain Topography, 32, 704–719. 10.1007/s10548-018-0691-2, [DOI] [PubMed] [Google Scholar]
- Sassenhagen J, & Draschkow D (2019). Cluster-based permutation tests of MEG/EEG data do not establish significance of effect latency or location. Psychophysiology, 56, e13335. 10.1111/psyp.13335, [DOI] [PubMed] [Google Scholar]
- Sauseng P, Tschentscher N, & Biel AL (2019). Be prepared: Tune to FM-theta for cognitive control. Trends in Neurosciences, 42, 307–309. 10.1016/j.tins.2019.02.006, [DOI] [PubMed] [Google Scholar]
- Schmitt LI, Wimmer RD, Nakajima M, Happ M, Mofakham S, & Halassa MM (2017). Thalamic amplification of cortical connectivity sustains attentional control. Nature, 545, 219–223. 10.1038/nature22073, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scimeca JM, Kiyonaga A, & D’Esposito M (2018). Reaffirming the sensory recruitment account of working memory. Trends in Cognitive Sciences, 22, 190–192. 10.1016/j.tics.2017.12.007, [DOI] [PubMed] [Google Scholar]
- Senoussi M, Verbeke P, Desender K, De Loof E, Talsma D, & Verguts T (2022). Theta oscillations shift towards optimal frequency for cognitive control. Nature Human Behaviour, 6, 1000–1013. 10.1038/s41562-022-01335-5, [DOI] [PubMed] [Google Scholar]
- Shine JM, Lewis LD, Garrett DD, & Hwang K (2023). The impact of the human thalamus on brain-wide information processing. Nature Reviews Neuroscience, 24, 416–430. 10.1038/s41583-023-00701-0, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sreenivasan KK, Curtis CE, & D’Esposito M (2014). Revisiting the role of persistent neural activity during working memory. Trends in Cognitive Sciences, 18, 82–89. 10.1016/j.tics.2013.12.001, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sreenivasan KK, & D’Esposito M (2019). The what, where and how of delay activity. Nature Reviews Neuroscience, 20, 466–481. 10.1038/s41583-019-0176-7, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczepanski SM, Crone NE, Kuperman RA, Auguste KI, Parvizi J, & Knight RT (2014). Dynamic changes in phase-amplitude coupling facilitate spatial attention control in fronto-parietal cortex. PLoS Biology, 12, e1001936. 10.1371/journal.pbio.1001936, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczepanski SM, & Knight RT (2014). Insights into human behavior from lesions to the prefrontal cortex. Neuron, 83, 1002–1018. 10.1016/j.neuron.2014.08.011, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torrence C, & Compo GP (1998). A practical guide to wavelet analysis. Bulletin of the American Meteorological Society, 79, 61–78. [DOI] [Google Scholar]
- van Ede F (2018). Mnemonic and attentional roles for states of attenuated alpha oscillations in perceptual working memory: A review. European Journal of Neuroscience, 48, 2509–2515. 10.1111/ejn.13759, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Veen BD, van Drongelen W, Yuchtman M, & Suzuki A (1997). Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. IEEE Transactions on Biomedical Engineering, 44, 867–880. 10.1109/10.623056, [DOI] [PubMed] [Google Scholar]
- Voytek B, Kayser AS, Badre D, Fegen D, Chang EF, Crone NE, et al. (2015). Oscillatory dynamics coordinating human frontal networks in support of goal maintenance. Nature Neuroscience, 18, 1318–1324. 10.1038/nn.4071, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallis JD, Anderson KC, & Miller EK (2001). Single neurons in prefrontal cortex encode abstract rules. Nature, 411, 953–956. 10.1038/35082081, [DOI] [PubMed] [Google Scholar]
- Wen H, & Liu Z (2016). Separating fractal and oscillatory components in the power spectrum of neurophysiological signal. Brain Topography, 29, 13–26. 10.1007/s10548-015-0448-0, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen X, Rangarajan G, & Ding M (2013). Multivariate Granger causality: An estimation framework based on factorization of the spectral density matrix. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 371, 20110610. 10.1098/rsta.2011.0610, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitfield-Gabrieli S, & Nieto-Castanon A (2012). Conn: A functional connectivity toolbox for correlated and anticorrelated brain networks. Brain Connectivity, 2, 125–141. 10.1089/brain.2012.0073, [DOI] [PubMed] [Google Scholar]
- Yeo BTT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, et al. (2011). The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of Neurophysiology, 106, 1125–1165. 10.1152/jn.00338.2011, [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Analysis scripts, behavioral data, preprocessed EEG data, and results of the group-level fMRI analyses are available on the Open Science Framework (https://osf.io/5vs2x/). Supplemental data and supporting files are available upon request via email to the lead author.


