Skip to main content

Advertisement

Springer Nature Link
Log in

Multi-scale UDCT dictionary learning based highly undersampled MR image reconstruction using patch-based constraint splitting augmented Lagrangian shrinkage algorithm

  • Published:
Frontiers of Information Technology & Electronic Engineering Aims and scope Submit manuscript

Abstract

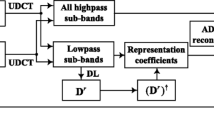
Recently, dictionary learning (DL) based methods have been introduced to compressed sensing magnetic resonance imaging (CS-MRI), which outperforms pre-defined analytic sparse priors. However, single-scale trained dictionary directly from image patches is incapable of representing image features from multi-scale, multi-directional perspective, which influences the reconstruction performance. In this paper, incorporating the superior multi-scale properties of uniform discrete curvelet transform (UDCT) with the data matching adaptability of trained dictionaries, we propose a flexible sparsity framework to allow sparser representation and prominent hierarchical essential features capture for magnetic resonance (MR) images. Multi-scale decomposition is implemented by using UDCT due to its prominent properties of lower redundancy ratio, hierarchical data structure, and ease of implementation. Each sub-dictionary of different sub-bands is trained independently to form the multi-scale dictionaries. Corresponding to this brand-new sparsity model, we modify the constraint splitting augmented Lagrangian shrinkage algorithm (C-SALSA) as patch-based C-SALSA (PB C-SALSA) to solve the constraint optimization problem of regularized image reconstruction. Experimental results demonstrate that the trained sub-dictionaries at different scales, enforcing sparsity at multiple scales, can then be efficiently used for MRI reconstruction to obtain satisfactory results with further reduced undersampling rate. Multi-scale UDCT dictionaries potentially outperform both single-scale trained dictionaries and multi-scale analytic transforms. Our proposed sparsity model achieves sparser representation for reconstructed data, which results in fast convergence of reconstruction exploiting PB C-SALSA. Simulation results demonstrate that the proposed method outperforms conventional CS-MRI methods in maintaining intrinsic properties, eliminating aliasing, reducing unexpected artifacts, and removing noise. It can achieve comparable performance of reconstruction with the state-of-the-art methods even under substantially high undersampling factors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Afonso, M.V., Bioucas-Dias, J.M., Figueiredo, M.A.T., 2011. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process., 20(3):681–695. [doi:10. 1109/TIP.2010.2076294]

    Article  MathSciNet  Google Scholar 

  • Aharon, M., Elad, M., Bruckstein, A., 2006. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process., 54(11): 4311–4322. [doi:10.1109/TSP.2006.881199]

    Article  Google Scholar 

  • Baraniuk, R., 2007. Compressive sensing. IEEE Signal Process. Mag., 24(4):118–121. [doi:10.1109/MSP.2007.4286571]

    Article  Google Scholar 

  • Candes, E.J., Donoho, D.L., 2004. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities. Commun. Pure Appl. Math., 57(2):219–266. [doi:10.1002/cpa.10116]

    Article  MathSciNet  MATH  Google Scholar 

  • Candes, E.J., Romberg, J., Tao, T., 2006a. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inform. Theory, 52(2):489–509. [doi:10.1109/TIT.2005.862083]

    Article  MathSciNet  MATH  Google Scholar 

  • Candes, E.J., Romberg, J.K., Tao, T., 2006b. Stable signal rcovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math., 59(8):1207–1223. [doi:10. 1002/cpa.20124]

    Article  MathSciNet  MATH  Google Scholar 

  • Chambolle, A., 2004. An algorithm for total variation minimization and applications. J. Math. Imag. Vis., 20(1-2): 89–97. [doi:10.1023/B:JMIV.0000011325.36760.1e]

    MathSciNet  Google Scholar 

  • Chen, C., Huang, J., 2014. The benefit of tree sparsity in accelerated MRI. Med. Image Anal., 18(6):834–842. [doi:10. 1016/j.media.2013.12.004]

    Article  Google Scholar 

  • Combettes, P.L., Wajs, V.R., 2005. Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul., 4(4):1168–1200. [doi:10.1137/050626090]

    Article  MathSciNet  MATH  Google Scholar 

  • Dahl, J., Hansen, P.C., Jensen, S.H., et al., 2010. Algorithms and software for total variation image reconstruction via first-order methods. Numer. Algor., 53(1):67–92. [doi:10. 1007/s11075-009-9310-3]

    Article  MathSciNet  MATH  Google Scholar 

  • Donoho, D.L., 2001. Sparse components of images and optimal atomic decompositions. Constr. Approx., 17(3): 353–382. [doi:10.1007/s003650010032]

    Article  MathSciNet  MATH  Google Scholar 

  • Donoho, D.L., 2006. Compressed sensing. IEEE Trans. Inform. Theory, 52(4):1289–1306. [doi:10.1109/TIT.2006.871582]

    Article  MathSciNet  MATH  Google Scholar 

  • Eckstein, J., Bertsekas, D.P., 1992. On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program., 55(1): 293–318. [doi:10.1007/BF01581204]

    Article  MathSciNet  MATH  Google Scholar 

  • Elad, M., 2010. Sparse and Redundant Representations: from Theory to Applications in Signal and Image Processing. Springer, New York, USA. [doi:10.1007/978-1-4419-7011-4]

    Book  Google Scholar 

  • Elad, M., Aharon, M., 2006. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process., 15(12):3736–3745. [doi:10.1109/TIP.2006.881969]

    Article  MathSciNet  Google Scholar 

  • Gabay, D., Mercier, B., 1976. A dual algorithm for the solution of nonlinear variational problems via finite element approximation. Comput. Math. Appl., 2(1):17–40. [doi:10. 1016/0898-1221(76)90003-1]

    Article  MATH  Google Scholar 

  • Gho, S.M., Nam, Y., Zho, S.Y., et al., 2010. Three dimension double inversion recovery gray matter imaging using compressed sensing. Magn. Reson. Imag., 28(10): 1395–1402. [doi:10.1016/j.mri.2010.06.029]

    Article  Google Scholar 

  • Huang, J., Zhang, S., Metaxas, D., 2011. Efficient MR image reconstruction for compressed MR imaging. Med. Image Anal., 15(5):670–679. [doi:10.1016/j.media.2011.06.001]

    Article  Google Scholar 

  • Kim, Y., Altbach, M.I., Trouard, T.P., et al., 2009. Compressed sensing using dual-tree complex wavelet transform. Proc. Int. Soc. Mag. Reson. Med., 17:2814.

    Google Scholar 

  • Kim, Y., Nadar, M.S., Bilgin, A., 2012. Wavelet-based compressed sensing using a Gaussian scale mixture model. IEEE Trans. Image Process., 21(6):3102–3108. [doi:10. 1109/TIP.2012.2188807]

    Article  MathSciNet  Google Scholar 

  • Lewicki, M.S., Sejnowski, T.J., 2000. Learning overcomplete representations. Neur. Comput., 12(2):337–365. [doi:10. 1162/089976600300015826]

    Article  Google Scholar 

  • Lin, L., 1989. A concordance correlation coefficient to evaluate reproducibility. Biometrics, 45(1):255–268. [doi:10. 2307/2532051]

    Article  MATH  Google Scholar 

  • Liu, Y., Cai, J., Zhan, Z., et al., 2015. Balanced sparse model for tight frames in compressed sensing magnetic resonance imaging. PLoS ONE, 10(4):e0119584.1–e0119584.19. [doi:10.1371/journal.pone.0119584]

    Google Scholar 

  • Lustig, M., Donoho, D., Pauly, J.M., 2007. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn. Reson. Med., 58(6):1182–1195. [doi:10.1002/mrm.21391]

    Article  Google Scholar 

  • Lustig, M., Donoho, D.L., Santos, J.M., et al., 2008. Compressed sensing MRI. IEEE Signal Process. Mag., 25(2):72–82. [doi:10.1109/MSP.2007.914728]

    Article  Google Scholar 

  • Mallat, S., 2008. A Wavelet Tour of Signal Processing: the Sparse Way (3rd Ed.). Academic Press, USA.

    Google Scholar 

  • Nguyen, T.T., Chauris, H., 2010. Uniform discrete curvelet transform. IEEE Trans. Signal Process., 58(7):3618–3634. [doi:10.1109/TSP.2010.2047666]

    Article  MathSciNet  Google Scholar 

  • Ning, B., Qu, X., Guo, D., et al., 2013. Magnetic resonance image reconstruction using trained geometric directions in 2D redundant wavelets domain and non-convex optimization. Magn. Reson. Imag., 31(9):1611–1622. [doi:10.1016/j.mri.2013.07.010]

    Article  Google Scholar 

  • Ophir, B., Lustig, M., Elad, M., 2011. Multi-scale dictionary learning using wavelets. IEEE J. Sel. Topics Signal Process., 5(5):1014–1024. [doi:10.1109/JSTSP.2011.2155032]

    Article  Google Scholar 

  • Qu, G., Zhang, D., Yan, P., 2002. Information measure for performance of image fusion. Electron. Lett., 38(7): 313–315. [doi:10.1049/el:20020212]

    Article  Google Scholar 

  • Qu, X., Zhang, W., Guo, D., et al., 2010. Iterative thresholding compressed sensing MRI based on contourlet transform. Inv. Probl. Sci. Eng., 18(6):737–758. [doi:10.1080/17415977.2010.492509]

    Article  MathSciNet  MATH  Google Scholar 

  • Qu, X., Guo, D., Ning, B., et al., 2012. Undersampled MRI reconstruction with patch-based directional wavelets. Magn. Reson. Imag., 30(7):964–977. [doi:10.1016/j.mri. 2012.02.019]

    Article  Google Scholar 

  • Qu, X., Hou, Y., Lam, F., et al., 2014. Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator. Med. Image Anal., 18(6):843–856. [doi:10.1016/j.media.2013.09.007]

    Article  Google Scholar 

  • Rauhut, H., Schnass, K., Vandergheynst, P., 2008. Compressed sensing and redundant dictionaries. IEEE Trans. Inform. Theory, 54(5):2210–2219. [doi:10.1109/TIT.2008. 920190]

    Article  MathSciNet  MATH  Google Scholar 

  • Ravishankar, S., Bresler, Y., 2011. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans. Med. Imag., 30(5):1028–1041. [doi:10.1109/TMI.2010.2090538]

    Article  Google Scholar 

  • Rubinstein, R., Zibulevsky, M., Elad, M., 2010. Double sparsity: learning sparse dictionaries for sparse signal approximation. IEEE Trans. Signal Process., 58(3): 1553–1564. [doi:10.1109/TSP.2009.2036477]

    Article  MathSciNet  Google Scholar 

  • Rudin, L.I., Osher, S., Fatemi, E., 1992. Nonlinear total variation based noise removal algorithms. Phys. D, 60(1-4): 259–268. [doi:10.1016/0167-2789(92)90242-F]

    Article  MATH  Google Scholar 

  • Trzasko, J., Manduca, A., 2009. Highly undersampled magnetic resonance image reconstruction via homotopic l 0-minimization. IEEE Trans. Med. Imag., 28(1):106–121. [doi:10.1109/TMI.2008.927346]

    Article  Google Scholar 

  • Wang, Z., Bovik, A.C., Sheikh, H.R., et al., 2004. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process., 13(4):600–612. [doi:10.1109/TIP.2003.819861]

    Article  Google Scholar 

  • Xydeas, C.S., Petrovic, V., 2000. Objective image fusion performance measure. Electron. Lett., 36(4):308–309. [doi:10.1049/el:20000267]

    Article  Google Scholar 

  • Zhu, Z., Wahid, K., Babyn, P., et al., 2013. Compressed sensing-based MRI reconstruction using complex doubledensity dual-tree DWT. Int. J. Biomed. Imag., 2013. 907501.1–907501.12. [doi:10.1155/2013/907501]

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Information Science & Engineering, Lanzhou University, Lanzhou, 730000, China

    Min Yuan, Bing-xin Yang, Yi-de Ma, Jiu-wen Zhang, Fu-xiang Lu & Tong-feng Zhang

Authors
  1. Min Yuan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Bing-xin Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yi-de Ma
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jiu-wen Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Fu-xiang Lu
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Tong-feng Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yi-de Ma.

Additional information

Project supported by the National Natural Science Foundation of China (Nos. 61175012 and 61201422), the Natural Science Foundation of Gansu Province of China (No. 1208RJ-ZA265), the Specialized Research Fund for the Doctoral Program of Higher Education of China (No. 2011021111-0026), and the Fundamental Research Funds for the Central Universities of China (Nos. lzujbky-2015-108 and lzujbky-2015-197)

ORCID: Min YUAN, http://orcid.org/0000-0001-7855-8678

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yuan, M., Yang, Bx., Ma, Yd. et al. Multi-scale UDCT dictionary learning based highly undersampled MR image reconstruction using patch-based constraint splitting augmented Lagrangian shrinkage algorithm. Frontiers Inf Technol Electronic Eng 16, 1069–1087 (2015). https://doi.org/10.1631/FITEE.1400423

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1631/FITEE.1400423

Keywords

CLC number