Published online by Cambridge University Press: 12 March 2014
Kleene [5] mentions two ways of extending the constructive ordinals. The first is by relativizing the set O of notations for the constructive ordinals, using fundamental sequences which are partial recursive in O. In this way we obtain the set OO which provides notations for the ordinals less than ω1O. Continuing the process, the sequence O, OO, 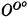 , … and the corresponding ordinals
, … and the corresponding ordinals 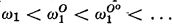 are obtained. A second possibility is to define (constructive) higher number classes in which partial recursive functions are used at limit ordinals to provide an “accessibility” mapping from a previously defined number class. The relationship between the ordinals obtained by the two methods of extension has been an open problem. Methods developed in this article are used to show that the two ways of extending the constructive ordinals are equivalent, provided the sets of notations for the higher number classes satisfy certain natural conditions. Equivalence is obtained, not only with respect to ordinals, but also with respect to the forms of the sets of notations for the higher number classes. Specifically, the fundamental fact that the sets of notations for the constructive ordinals are complete Π11 sets generalizes to suitably defined higher number classes. As an application we prove that the ordinals of the Addison and Kleene [1] constructive third number class are exactly the ordinals less than ω1O and the set
are obtained. A second possibility is to define (constructive) higher number classes in which partial recursive functions are used at limit ordinals to provide an “accessibility” mapping from a previously defined number class. The relationship between the ordinals obtained by the two methods of extension has been an open problem. Methods developed in this article are used to show that the two ways of extending the constructive ordinals are equivalent, provided the sets of notations for the higher number classes satisfy certain natural conditions. Equivalence is obtained, not only with respect to ordinals, but also with respect to the forms of the sets of notations for the higher number classes. Specifically, the fundamental fact that the sets of notations for the constructive ordinals are complete Π11 sets generalizes to suitably defined higher number classes. As an application we prove that the ordinals of the Addison and Kleene [1] constructive third number class are exactly the ordinals less than ω1O and the set  of notations for their third number class is recursively isomorphic to OO.
of notations for their third number class is recursively isomorphic to OO.
Research for this article was begun while the author was a National Science Foundation Predoctoral Fellow. Some of the material presented here is contained in the author's Ph.D. thesis [10] and was presented by title [11] to the American Mathematical Society, February, 1964.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.