Published online by Cambridge University Press: 12 March 2014
In the fourth edition of Hilbert-Ackermann's Grundzüge der Theoretischen Logik (Springer-Verlag: Berlin-Göttingen-Heidelberg 1959) the following assertion is “proved” (p. 131):
Ein Ausdruck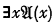 , der keine freien Individuenvariablen enthält, ist dann und nur dann allgemeingültig, wenn
, der keine freien Individuenvariablen enthält, ist dann und nur dann allgemeingültig, wenn 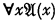 allgemeingültig ist. Die Ausdrücke, die die Identität enthalten, sind dabei eingeschlossen.
allgemeingültig ist. Die Ausdrücke, die die Identität enthalten, sind dabei eingeschlossen.
As a counter example one can cite: ∃x(¬∃xFx ∨ Fx), which is universally valid yet the generalized form: ∀x(¬∃xFx ∨ Fx) is not (e.g. let the domain of individuals be the natural numbers and let ‘Fx’ be ‘x is factorable’).
It may be of interest to see where the alleged proof went astray. It is argued (correctly) that any expression 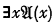 can only be derived by the given rules from a formula
can only be derived by the given rules from a formula 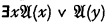 , or from this formula with any other variable in place of y. Moreover (still correctly) any upper formula of such a formula is of the form
, or from this formula with any other variable in place of y. Moreover (still correctly) any upper formula of such a formula is of the form 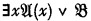 (“Upper formula” in the transitive sense of an upper formula of an upper formula being an upper formula). But then it is stated (incorrectly) that if
(“Upper formula” in the transitive sense of an upper formula of an upper formula being an upper formula). But then it is stated (incorrectly) that if 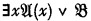 is an upper formula of
is an upper formula of 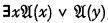 , then
, then 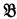 is an upper formula of
is an upper formula of 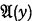 . To show that this is incorrect we here append a proof of the universally valid formula mentioned above:
. To show that this is incorrect we here append a proof of the universally valid formula mentioned above:
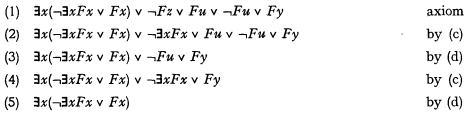
This work was supported by the United States Atomic Energy Commission. Reproduction in whole or in part is permitted for any purpose of the U.S. Government.
1 This work was supported by the United States Atomic Energy Commission. Reproduction in whole or in part is permitted for any purpose of the U.S. Government.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.