Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-17T07:08:51.359Z Has data issue: false hasContentIssue false
  • English
  • Français

On spectra, and the negative solution of the decision problem for identities having a finite nontrivial model1

Published online by Cambridge University Press:  12 March 2014

Ralph Mckenzie
Ralph Mckenzie*
Affiliation:
University of California, Berkeley, California 94720
Get access Rights & Permissions [Opens in a new window]

Extract

An algorithm has been described by S. Burris [3] which decides if a finite set of identities, whose function symbols are of rank at most 1, has a finite, nontrivial model. (By “nontrivial” it is meant that the universe of the model has at least two elements.) As a consequence of some results announced in the abstracts [2] and [8], it is clear that if the restriction on the ranks of function symbols is relaxed somewhat, then this finite model problem is no longer solvable by an algorithm, or at least not by a “recursive algorithm” as the term is used today.

In this paper we prove a sharp form of this negative result; showing, by the way, that Burris' result is in a sense the best possible result in the positive direction. Our main result is that in a first order language whose only function or relation symbol is a 2-place function symbol 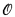(the language of groupoids), the set of identities 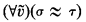that have no nontrivial model, is recursively inseparable from the set of identities 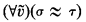such that the sentence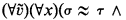 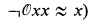has a finite model. As a corollary, we have that each of the following problems, restricted to sentences defined in the language of groupoids, is algorithmically unsolvable: (1) to decide if an identity has a finite nontrivial model; (2) to decide if an identity has a nontrivial model; (3) to decide if a universal sentence has a finite model; (4) to decide if a universal sentence has a model. We note that the undecidability of (2) was proved earlier by McNulty [13, Theorem 3.6(i)], improving results obtained by Murskiǐ [14] and by Perkins [17]. The other parts of the corollary seem to be new.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 40 , Issue 2 , June 1975 , pp. 186 - 196
Copyright
Copyright © Association for Symbolic Logic 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The main result of this paper was announced in [12].

References

REFERENCES

[1]Bell, J. L. and Slomson, A. B., Models and ultraproducts: An introduction, North-Holland, Amsterdam, 1969.Google Scholar
[2]Bennett, J. H., Equational spectra, this Journal, vol. 30 (1965), p. 264.Google Scholar
[3]Burris, S., Models in equational theories of unary algebras, Algebra Universalis, vol. 1 (1972), pp. 386–392.CrossRefGoogle Scholar
[4]Ershov, Yu. L., Lavrov, I. A., Taimanov, A. D. and Taitslin, M. A., Elementary theories, Russian Mathematical Surveys, vol. 20 (1965).CrossRefGoogle Scholar
[5]Evans, T., The spectrum of a variety, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 13 (1967), pp. 213–218.CrossRefGoogle Scholar
[6]Grätzer, G., Universal algebra, Van Nostrand, Princeton, N.J., 1968.Google Scholar
[7]Grätzer, G., On the spectra of classes of algebras, Proceedings of the American Mathematical Society, vol. 18 (1967), pp. 729–735.CrossRefGoogle Scholar
[8]Grätzer, G. and McKenzie, R., Equational spectra and reduction of identities, Notices of the American Mathematical Society, vol. 14 (1967), p. 697.Google Scholar
[9]Henkin, L., Monk, J. D. and Tarski, A., Cylindric algebras: I, North-Holland, Amsterdam, 1971.Google Scholar
[10]Lavrov, I. A., Effective inseparability of the sets of identically true formulae and finitely refutable formulae for certain elementary theories, Algebra i Logika (2), vol. 1 (1963), pp. 5–19.Google Scholar
[11]McKenzie, R., Equational bases for lattice theories, Mathematica Scandinavica, vol. 27 (1970), pp. 24–38.CrossRefGoogle Scholar
[12]McKenzie, R., Simple undecidable problems about finite groupoids, Notices of the American Mathematical Society, vol. 20 (1973), A–505.Google Scholar
[13]McNulty, G., The decision problem for equational bases of algebras, Thesis, University of California, Berkeley, 1971.Google Scholar
[14]Murskiǐ, V. L., Nondiscernible properties of finite systems of identity relations, Doklady Academii Nauk SSSR, vol. 196 (1971), pp. 520–522; English transl., Soviet Mathematics. Doklady, vol. 12 (1971), pp. 183–186.Google Scholar
[15]Neumann, B. H., On a problem of G. Grätzer, Publicationes Mathematicae (Debrecen).Google Scholar
[16]Padmanabhan, R. and Quackenbush, R. W., Equational theories of algebras with distributive congruences, Proceedings of the American Mathematical Society, vol. 41 (1973), pp. 373–377.CrossRefGoogle Scholar
[17]Perkins, P., Unsolvable problems for equational theories, Notre Dame Journal Formal Logic, vol. 8 (1967), pp. 175–185.CrossRefGoogle Scholar
[18]Pixley, A. F., The ternary discriminator function in universal algebra, Mathematische Annalen, vol. 191 (1971), pp. 167–180.CrossRefGoogle Scholar
[19]Rogers, H. Jr., Theory of recursive functions and effective comput ability, McGraw-Hill, New York, 1967.Google Scholar
[20]Tarski, A., Equational logic and equational theories of algebras, Contributions to mathematical logic (Schütte, K., Editor), North-Holland, Amsterdam, 1968, pp. 275–288.Google Scholar