Published online by Cambridge University Press: 12 March 2014
In this paper, we give consistency proofs for the existence of a κ-saturated ideal on an inaccessible κ, and for the existence of an ω2-saturated ideal on ω1. We also include an historical survey outlining other known results on saturated ideals.
§1. Forcing. We assume that the reader is familiar with the usual techniques in forcing and Boolean-valued models (see Jech [3] or Rosser [11]), so we shall just specify here some of the less standard notation.
“cBa” abbreviates “complete Boolean algebra”.
If P (= ‹P, <›) is a notion of forcing, 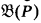 is the associated cBa. We write VP for
is the associated cBa. We write VP for 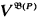 .
.
Notions like κ-closed, κ-complete, etc. always mean < κ. Thus, P is κ-closed iff every decreasing chain of length less than κ has a lower bound, and a Boolean algebra 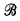 is κ-complete iff sups of subsets of
is κ-complete iff sups of subsets of 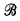 of cardinality less than κ always exist.
of cardinality less than κ always exist.
If 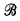 is a cBa, x̌ is the object in
is a cBa, x̌ is the object in 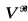 representing x in V. In many cases, especially with ordinals, the ̌ is dropped. V̌ is the Boolean-valued class representing V — i.e.,
representing x in V. In many cases, especially with ordinals, the ̌ is dropped. V̌ is the Boolean-valued class representing V — i.e.,
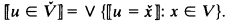
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.