Published online by Cambridge University Press: 12 March 2014
Bachmann, in [2] shows how certain ordinals <Ω(Ω = Ω1 where Ωξ is the (1 + ξ)th infinite initial ordinal) may be described from below using suitable descriptions of ordinals <Ω2. The aim of this paper is to consider another approach to describing ordinal <Ω and compare it with the Bachmann method. Our approach will use functionals of transfinite type based on Ω.
The Bachmann method consists in denning a hierarchy 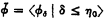 of normal functions ϕδ: Ω → Ω (i.e. continuous and strictly increasing) for δ ≤ η0 < Ω2, starting with ϕ0(λ) = ω1 + λ. The definition of
of normal functions ϕδ: Ω → Ω (i.e. continuous and strictly increasing) for δ ≤ η0 < Ω2, starting with ϕ0(λ) = ω1 + λ. The definition of 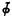 depends on a suitable description of the ordinals ≤ η0. This is obtained by defining a hierarchy 〈Fδ ∣ δ ≤ Ω2〉 of normal functions Fδ: Ω2 → Ω2 analogously to the definition of the initial segment 〈ϕδ ∣ δ ≤ Ω〉 of
depends on a suitable description of the ordinals ≤ η0. This is obtained by defining a hierarchy 〈Fδ ∣ δ ≤ Ω2〉 of normal functions Fδ: Ω2 → Ω2 analogously to the definition of the initial segment 〈ϕδ ∣ δ ≤ Ω〉 of 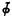 . The ordinal η0 is
. The ordinal η0 is 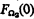 .
.
Note. Our description of Bachmann's hierarchies will differ slightly from those in Bachmann's paper. Let 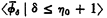 and
and 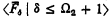 denote the hierarchies in [2]. Then as Bachmann's normal functions are not defined at 0 we let
denote the hierarchies in [2]. Then as Bachmann's normal functions are not defined at 0 we let 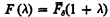 for λ, δ < Ω2. Bachmann defines
for λ, δ < Ω2. Bachmann defines 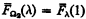 for 0 < λ < Ω2 but it seems more natural to omit this so that we let
for 0 < λ < Ω2 but it seems more natural to omit this so that we let 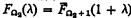 . The situation is analogous for
. The situation is analogous for 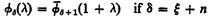 and leads to the following definitions:
and leads to the following definitions:
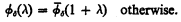
where n < ω and ξ is a limit number of cofinality Ω, and
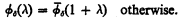
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.