In this paper we will present an application of generalized recursion theory to (noncombinatorial) set theory. More precisely we will combine a priority argument in α-recursion theory with a forcing construction to prove a theorem about the interdefinability of certain subsets of admissible ordinals.

Our investigation was prompted by G. Sacks and S. Simpson asking [6] if it is obvious that there are, for each Σn-admissible α, Σn (over Lα) subsets of α which are Δn-incomparable. If one understands “B is Δn in C” to mean that there are Σn/Lα reduction procedures which put out B and 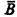when one feeds in C, then the answer is an unqualified “yes.” In this sense “Δn in” is a direct generalization of “α-recursive in” (replace Σ1 by Σn in the definition) and so amenable to the methods of [7, §§3, 5]. Indeed one simply chooses a complete Σn−1 set A and mimics the construction of [6] as modified in [7, §5] to produce two α-A-r.e. sets B and C neither of which is α-A-recursive in the other. By the remarks on translation [7, §3] this will immediately give the desired result for this definition of “Δn in.”

There is, however, the more obvious and natural notion of “Δn in” to be considered: B is Δn in C iff there are Σn and Πn formulas of ⟨Lα, C⟩ which define B.